
山西佛源宇花 SHANXI INSTITUTE OF ENEROY 第九章辐射换热的计算 固体表面间的辐射换热 1
1 第九章 辐射换热的计算 固体表面间的辐射换热

山西佛源宇花 SHANXI INSTITUTE OF ENEROY 影响因素: 表面的辐射性质 表面温度 面积、形状 表面间的相对位置 2
2 表面的辐射性质 表面温度 面积、形状 表面间的相对位置 影响因素:

山西感源宇花 SHANXI INSTITUTE OF ENEROY 9.1辐射传热的角系数 两个表面之间的辐射换热量与两个表面之间的相对位 置有很大关系 T T1、\(1 7 T 2 (a) (b) 3
3 9.1 辐射传热的角系数 两个表面之间的辐射换热量与两个表面之间的相对位 置有很大关系

山五限源宇花 HANXI IN台TITUT老OF ENEROY 1.角系数的概念 ■角系数的定义 表面1发出的辐射能中落到表面2百分数称为表面1对表面2 的角系数 1表面发出落在2表面上的辐射能 表面的辐射能 表面1对表面2的角系数X1,2 假设:(1)漫表面,即物体的辐射强度及反射的辐射轻度与 方向无关 (2)物体表面的辐射物性均匀,即温度均匀、发射率及反射 率均匀 4
4 假设:(1)漫表面,即物体的辐射强度及反射的辐射轻度与 方向无关 (2)物体表面的辐射物性均匀,即温度均匀、发射率及反射 率均匀 1. 角系数的概念 表面 的辐射能 表面发出落在 表面上的辐射能 1 1 2 X1,2 = 表面1对表面2的角系数 X 1,2 角系数的定义 表面1发出的辐射能中落到表面2百分数称为表面1对表面2 的角系数

山多破源宇花 SHANXI INSTITUTE OF ENEROY 2.角系数的性质 dA: 在这两个假设条件下,物体的表 面温度及发射率的改变只能影响 该物体向外发射的辐射能的多少 而不能影响在空间的相对分布。 角系数是一个纯几何因子 ■角系数的相对性 dA,不 两微元面间的辐射 5
5 2. 角系数的性质 两微元面间的辐射 在这两个假设条件下,物体的表 面温度及发射率的改变只能影响 该物体向外发射的辐射能的多少 而不能影响在空间的相对分布。 角系数是一个纯几何因子 角系数的相对性
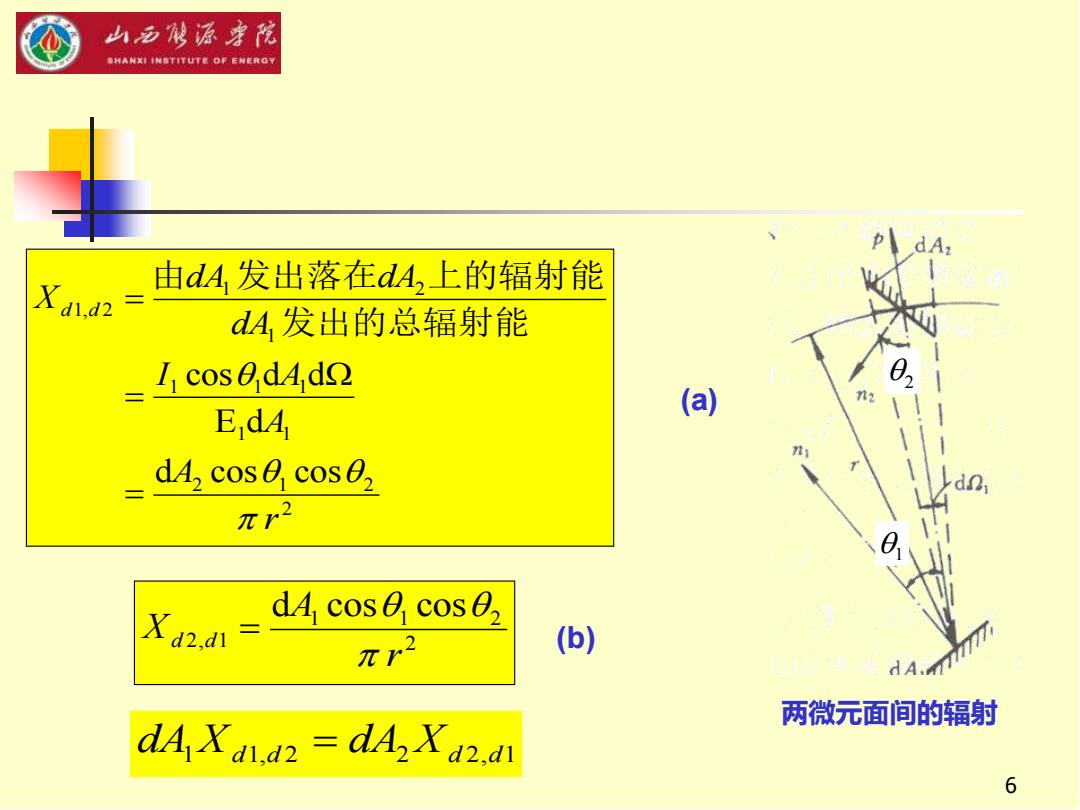
山西城源李院 参HANXI INSTITUT老OF ENEROY dA: 由dA,发出落在dA,上的辐射能 Xdl.d2= dA发出的总辐射能 I cosedA d (a) n2 Ed4 d4,cose,cose πr2 元r2 (b) dA. 两微元面间的辐射 dA Xd.d2 dAzXd2.d 6
6 2 2 1 2 1 1 1 1 1 1 1 2 1, 2 d cos cos E d cos d d r A A I A dA dA dA Xd d = = = 发出的总辐射能 由 发出落在 上的辐射能 2 1 1 2 2, 1 d cos cos r A Xd d = (a) (b) 两微元面间的辐射 1 2 dA1 Xd1,d 2 = dA2 Xd 2,d1

山西城源李院 SHANXI INSTITUTE OF ENEROY 对两个有限大小表面A,、A,之间角系数可表示为 πr2 A .=匹99出 π2 d4 Xd2.=Ja.Xa2.d x: AX1.2=A2X21 7
7 = 1 2,1 2, 1 A Xd Xd d 对两个有限大小表面 A1 、 A2 之间角系数可表示为 = = 1 2 1 2 1, 2 1 1 2 1 2 1 2 1 1,2 d 1 cos cos d d 1 A A d d A A X A r A A A A X = 1 2 2, 1 2 2 2,1 d 1 A A Xd d A A X == = 1 2 1 2 2 2 , 1 2 1,2 cos cos dA A dA A d dA r X A1 X1,2 = A2 X2,1
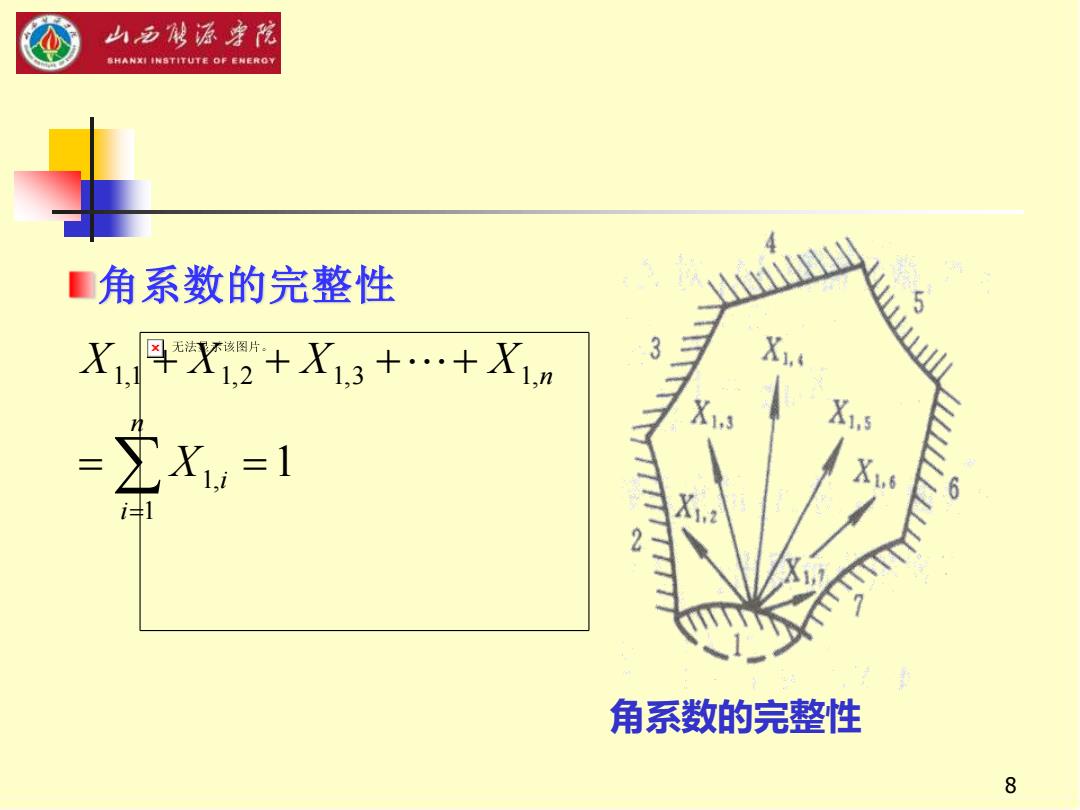
山莎移源宇花 SHANXI INSTITUTE OF ENEROY ■角系数的完整性 X4X12+X1.3+…+X1m X1. X =∑Xw=1 i41 角系数的完整性 8
8 角系数的完整性 1 1 1, 1,1 1,2 1,3 1, = = + + ++ = n i i n X X X X X 角系数的完整性
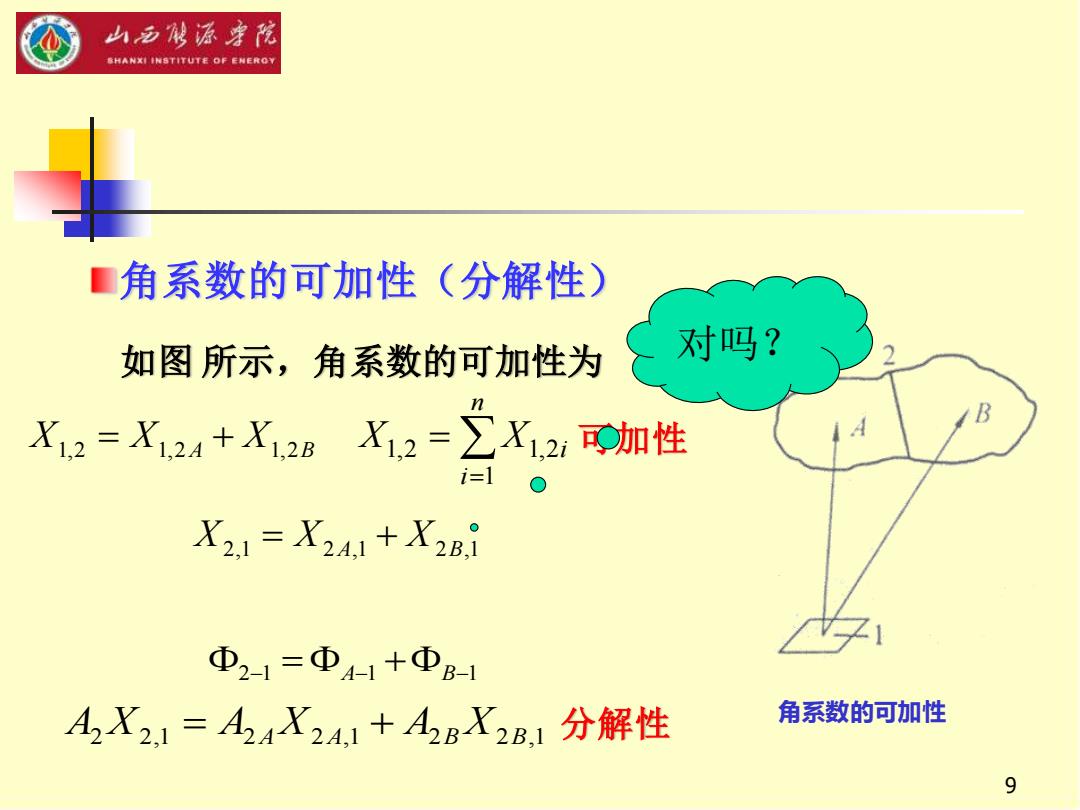
山多能源宇院 SHANXI INSTITUTE OF ENEROY ■角系数的可加性(分解性) 如图所示,角系数的可加性为 对吗? X12=X24+X12BX12=∑X12,可加性 i=l X21=X241+X2B,i Φ21=ΦA1+ΦB-1 A2X2,1=A24X24,1+A2BX2B,1分解性 角系数的可加性 9
9 = = n i X X i 1 1,2 1,2 角系数的可加性 如图 所示,角系数的可加性为 角系数的可加性(分解性) A2 X2,1 = A2A X2A,1 + A2B X2B,1 2−1 = A−1 +B−1 可加性 分解性 X1,2 = X1,2A + X1,2B X2,1 = X2A,1 + X2B,1 对吗?

山多能源宇花 SHANXI INSTITUTE OF ENEROY 3.角系数的计算方法 求解角系数的方法主要有直接积分法、代数分析法 ■直接积分法 图9-18w20 ■代数分析法 利用角系数的三个性质:相对性、完整性、可加性,通过 求解代数方程来获得角系数的方法 10
10 3. 角系数的计算方法 求解角系数的方法主要有直接积分法、代数分析法 直接积分法 代数分析法 图9-18~20 利用角系数的三个性质:相对性、完整性、可加性,通过 求解代数方程来获得角系数的方法