
第一章 思考题 1.试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。 答:导热和对流的区别在于:物体内部依靠微观粒子的热运动而产生的热量传递现象,称为导 热:对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。联系是:在发生对流 换热的同时必然伴生有导热。 导热、对流这两种热量传递方式,只有在物质存在的条件下才能实现,而辐射可以在真空中传 播,辐射换热时不仅有能 量的转移还伴有能量形式的转换。 2.以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩一玻耳滋曼定律是应当熟记的传热学公 式。试写出这三个公式并说明其中每一个符号及其意义。 dt q=-1 dt 答:①傅立叶定律: dx,其中,q一热流密度:)一导热系数:dx一沿x方向的温 度变化率,“一”表示热量传递的方向是沿着温度降低的方向。 ②牛顿冷却公式:q=h(tw-t:),其中,q一热流密度:h-表面传热系数: tw一固体 表面温度:t:一流体的温度。 ③斯忒藩一玻耳兹曼定律: q=σT4,其中,q一热流密度:。一斯忒藩一玻耳兹曼常数: T一辐射物体的热力学温度。 3.导热系数、表面传热系数及传热系数的单位各是什么?哪些是物性参数,哪些与过程有关? 答:①导热系数的单位是:W(.):②表面传热系数的单位是: WW(m2.K:③传热系数的 单位是:W(m2.)。这三个参数中,只有导热系数是物性参数,其它均与过程有关。 4.当热量从壁面一侧的流体穿过壁面传给另一侧的流体时,冷、热流体之间的换热量可以通过其 中任何一个环节来计算(过程是稳态的),但本章中又引入了传热方程式,并说它是“换热器热 工计算的基本公式”。试分析引入传热方程式的工程实用意义。 答:因为在许多工业换热设备中,进行热量交换的冷、热流体也常处于固体壁面的两侧,是工 程技术中经常遇到的一种典型热量传递过程。 5. 用铝制的水壶烧开水时,尽管炉火很旺,但水壶仍然安然无恙。而一旦壶内的水烧干后,水壶 很快就烧坏。试从传热学的观点分析这一现象。 答:当壶内有水时,可以对壶底进行很好的冷却(水对壶底的对流换热系数大) ,壶底的热量被 很快传走而不至于温度升得很高:当没有水时,和壶底发生对流换热的是气体,因为气体发生 对流换热的表面换热系数小,壶底的热量不能很快被传走,故此壶底升温很快,容易被烧坏。 6. 用一只手握住盛有热水的杯子,另一只手用筷子快速搅拌热水,握杯子的手会显著地感到热。 试分析其原因。 答:当没有搅拌时,杯内的水的流速几乎为零,杯内的水和杯壁之间为自然对流换热,自热对 流换热的表面传热系数小,当快速搅拌时,杯内的水和杯壁之间为强制对流换热,表面传热系 数大,热水有更多的热量被传递到杯壁的外侧,因此会显著地感觉到热。 7.什么是串联热阻叠加原则,它在什么前提下成立?以固体中的导热为例,试讨论有哪些情况可 能使热量传递方向上不同截面的热流量不相等。 答:在一个串联的热量传递过程中,如果通过每个环节的热流量都相同,则各串联环节的总热 阻等于各串联环节热阻的和。例如:三块无限大平板叠加构成的平壁。例如通过圆筒壁,对于 各个传热环节的传热面积不相等,可能造成热量传递方向上不同截面的热流量不相等。 8.有两个外形相同的保温杯A与B,注入同样温度、同样体积的热水后不久,A杯的外表面就可以 感觉到热,而B杯的外表面则感觉不到温度的变化,试问哪个保温杯的质量较好? 答:B:杯子的保温质量好。因为保温好的杯子热量从杯子内部传出的热量少,经外部散热以 后,温度变化很小,因此几乎感觉不到热。 能量平衡分析 1-1夏天的早晨,一个大学生离开宿舍时的温度为 20℃。他希望晚上回到房间时的温度能够低一些, 【第1页共284页】
【第 1 页 共 284 页】 第一章 思考题 1. 试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。 答: 导热和对流的区别在于:物体内部依靠微观粒子的热运动而产生的热量传递现象,称为导 热;对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。联系是:在发生对流 换热的同时必然伴生有导热。 导热、对流这两种热量传递方式,只有在物质存在的条件下才能实现,而辐射可以在真空中传 播,辐射换热时不仅有能 量的转移还伴有能量形式的转换。 2. 以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩-玻耳兹曼定律是应当熟记的传热学公 式。试写出这三个公式并说明其中每一个符号及其意义。 答: ① 傅立叶定律: dx dt q ,其中, q-热流密度; -导热系数; dx dt -沿 x 方向的温 度变化率,“-”表示热量传递的方向是沿着温度降低的方向。 ② 牛顿冷却公式: ( ) w f q h t t ,其中, q -热流密度; h-表面传热系数; t w -固体 表面温度; f t -流体的温度。 ③ 斯忒藩-玻耳兹曼定律: 4 q T ,其中, q -热流密度; -斯忒藩-玻耳兹曼常数; T -辐射物体的热力学温度。 3. 导热系数、表面传热系数及传热系数的单位各是什么?哪些是物性参数,哪些与过程有关? 答: ① 导热系数的单位是: W/(m.K) ;② 表面传热系数的单位是: W/(m 2 .K) ;③ 传热系数的 单位是: W/(m 2 .K)。这三个参数中,只有导热系数是物性参数,其它均与过程有关。 4. 当热量从壁面一侧的流体穿过壁面传给另一侧的流体时,冷、热流体之间的换热量可以通过其 中任何一个环节来计算(过程是稳态的) ,但本章中又引入了传热方程式,并说它是“换热器热 工计算的基本公式” 。试分析引入传热方程式的工程实用意义。 答: 因为在许多工业换热设备中,进行热量交换的冷、热流体也常处于固体壁面的两侧,是工 程技术中经常遇到的一种典型热量传递过程。 5. 用铝制的水壶烧开水时,尽管炉火很旺,但水壶仍然安然无恙。而一旦壶内的水烧干后,水壶 很快就烧坏。试从传热学的观点分析这一现象。 答: 当壶内有水时,可以对壶底进行很好的冷却(水对壶底的对流换热系数大) ,壶底的热量被 很快传走而不至于温度升得很高;当没有水时,和壶底发生对流换热的是气体,因为气体发生 对流换热的表面换热系数小,壶底的热量不能很快被传走,故此壶底升温很快,容易被烧坏。 6. 用一只手握住盛有热水的杯子,另一只手用筷子快速搅拌热水,握杯子的手会显著地感到热。 试分析其原因。 答: 当没有搅拌时,杯内的水的流速几乎为零,杯内的水和杯壁之间为自然对流换热,自热对 流换热的表面传热系数小,当快速搅拌时,杯内的水和杯壁之间为强制对流换热,表面传热系 数大,热水有更多的热量被传递到杯壁的外侧,因此会显著地感觉到热。 7. 什么是串联热阻叠加原则,它在什么前提下成立?以固体中的导热为例,试讨论有哪些情况可 能使热量传递方向上不同截面的热流量不相等。 答: 在一个串联的热量传递过程中,如果通过每个环节的热流量都相同,则各串联环节的总热 阻等于各串联环节热阻的和。例如:三块无限大平板叠加构成的平壁。例如通过圆筒壁,对于 各个传热环节的传热面积不相等,可能造成热量传递方向上不同截面的热流量不相等。 8.有两个外形相同的保温杯 A 与 B,注入同样温度、同样体积的热水后不久, A 杯的外表面就可以 感觉到热,而 B 杯的外表面则感觉不到温度的变化,试问哪个保温杯的质量较好? 答:B:杯子的保温质量好。因为保温好的杯子热量从杯子内部传出的热量少,经外部散热以 后,温度变化很小,因此几乎感觉不到热。 能量平衡分析 1-1 夏天的早晨,一个大学生离开宿舍时的温度为 20℃。他希望晚上回到房间时的温度能够低一些

于是早上离开时紧闭门窗,并打开了一个功率为15W的电风扇,该房间的长、宽、高分别为 5m、 3m、2.5m。如果该大学生10h以后回来,试估算房间的平均温度是多少? 解:因关闭门窗户后,相当于隔绝了房间内外的热交换,但是电风扇要在房间内做工产生热量:为 15×10×3600=540000J全部被房间的空气吸收而升温,空气在 20℃时的比热为:1.005KJ/Kg.K, 540000×103 △t= =11.89 密度为1.205Kg1m3,所以 5×3×2.5×1.205×1.005 当他回来时房间的温度近似为32℃。 1-2理发吹风器的结构示意图如附图所示,风道的流通面积 A2=60cm,进入吹风器的空气压力 p=100kPa,温度t1=25℃。要求吹风器出口的空气温度 t2=47℃,试确定流过吹风器的空气 的质量流量以及吹风器出口的空气平均速度。电加热器的功率为 1500W. 解: 1-3淋浴器的喷头正常工作时的供水量一般为每分钟 1000cm3。冷水通过电热器从 15℃被加热到 43℃。试问电热器的加热功率是多少?为了节省能源, 有人提出可以将用过后的热水(温度为38℃) 送入一个换热器去加热进入淋浴器的冷水。如果该换热器能将冷水加热到 27℃,试计算采用余热回 收换热器后洗澡15min可以节省多少能源? 解:电热器的加热功率: P_Q_cmt_4.18×10°×102×100×10×(43-15)-1950.6W=1.95kW T 60 15分钟可节省的能量: Q=cm△t=4.18×10×10×1000×10×15×(27-15=752400J=752.4kJ 1-4对于附图所示的两种水平夹层,试分析冷、热表面间热量交换的方式有何不同?如果要通过实验 来测定夹层中流体的导热系数,应采用哪一种布置? 物面 诊五 LLELLELCLLLLL1LLI L山 3哈经德 3粉德。 ntttitiittitttan r l t i l t t i t t t 面 流科 解:(a)中热量交换的方式主要为热传导。 (b)热量交换的方式主要有热传导和自然对流。 所以如果要通过实验来测定夹层中流体的导热系数,应采用( a)布置。 1-5一个内部发热的圆球悬挂于室内,对于附图所示的三种情况,试分析: (1)圆球表面散热的方 式:(2)圆球表面与空气之间的换热方式。 解:(2)圆球为表面传热方式散热。 (1)换热方式:(a)自然对流换热;(b)自然对流与强制对流换热相当的过渡流传热: (c)强制对 流换热: 1-6一字宙飞船的外形示于附图中,其中外遮光罩是凸出于飞船体之外的一个光学窗口,其表面的 温度状态直接影响到飞船的光学遥感器。船体表面各部分的表面温度与遮光罩的表面温度不同。试 分析,飞船在太空中飞行时与遮光罩表面发生热交换的对象可能有哪些?换热的方式是什么? 解:一遮光罩与外界发生辐射换热及遮光罩外表与船体外表进行辐射。传热方式为(辐射) 1-7热电偶常用来测量气流温度。如附图所示,用热电偶来测量管道中高温气流的温度 Tr 壁管温度Tw<T:。试分析热电偶结点的换热方式。 解:具有管道内流体对节点的对流换热,沿偶丝到节点的导热和管道内壁到节点的热辐射。 【第2页共284页】
【第 2 页 共 284 页】 于是早上离开时紧闭门窗,并打开了一个功率为 15W 的电风扇,该房间的长、宽、高分别为 5m、 3m、2.5m。如果该大学生 10h 以后回来,试估算房间的平均温度是多少? 解: 因关闭门窗户后,相当于隔绝了房间内外的热交换,但是电风扇要在房间内做工产生热量:为 15 10 3600=540000J 全部被房间的空气吸收而升温,空气在 20℃时的比热为: 1.005KJ/Kg.K, 密度为 1.205Kg/m 3 ,所以 11.89 5 3 2.5 1.205 1.005 540000 10 3 t 当他回来时房间的温度近似为 32℃。 1-2 理发吹风器的结构示意图如附图所示,风道的流通面积 2 A2 60cm ,进入吹风器的空气压力 p 100kPa ,温度 t1 25℃。要求吹风器出口的空气温度 t2 47 ℃,试确定流过吹风器的空气 的质量流量以及吹风器出口的空气平均速度。电加热器的功率为 1500W。 解: 1-3 淋浴器的喷头正常工作时的供水量一般为每分钟 3 1000cm 。冷水通过电热器从 15℃被加热到 43℃。试问电热器的加热功率是多少?为了节省能源, 有人提出可以将用过后的热水 (温度为 38℃) 送入一个换热器去加热进入淋浴器的冷水。如果该换热器能将冷水加热到 27℃,试计算采用余热回 收换热器后洗澡 15min 可以节省多少能源? 解: 电热器的加热功率: W kW Q cm t P 1950.6 1.95 60 4.18 10 10 1000 10 (43 15) 3 3 6 15 分钟可节省的能量: Q cm t 4.18 10 10 1000 10 15 (27 15) 752400J 752.4kJ 3 3 6 1-4 对于附图所示的两种水平夹层, 试分析冷、 热表面间热量交换的方式有何不同?如果要通过实验 来测定夹层中流体的导热系数,应采用哪一种布置? 解:(a)中热量交换的方式主要为热传导。 (b)热量交换的方式主要有热传导和自然对流。 所以如果要通过实验来测定夹层中流体的导热系数,应采用( a)布置。 1-5 一个内部发热的圆球悬挂于室内,对于附图所示的三种情况,试分析: (1)圆球表面散热的方 式;(2)圆球表面与空气之间的换热方式。 解:(2)圆球为表面传热方式散热。 (1)换热方式:(a)自然对流换热; ( b)自然对流与强制对流换热相当的过渡流传热; (c)强制对 流换热; 1-6 一宇宙飞船的外形示于附图中,其中外遮光罩是凸出于飞船体之外的一个光学窗口,其表面的 温度状态直接影响到飞船的光学遥感器。船体表面各部分的表面温度与遮光罩的表面温度不同。试 分析,飞船在太空中飞行时与遮光罩表面发生热交换的对象可能有哪些?换热的方式是什么? 解: 一遮光罩与外界发生辐射换热及遮光罩外表与船体外表进行辐射。传热方式为(辐射) 1-7 热电偶常用来测量气流温度。如附图所示,用热电偶来测量管道中高温气流的温度 Tf ,壁管温度 Tw T f 。试分析热电偶结点的换热方式。 解:具有管道内流体对节点的对流换热,沿偶丝到节点的导热和管道内壁到节点的热辐射

1-8热水瓶胆剖面的示意图如附图所示。瓶胆的两层玻璃之间抽成真空,内胆外壁及外胆内壁涂了 反射率很低的银。试分析热水瓶具有保温作用的原因。如果不小心破坏了瓶胆上抽气口处的密闭性, 这会影响保温效果吗? 解:保温作用的原因:内胆外壁外胆内壁涂了反射率很低的银,则通过内外胆向外辐射的热量很少, 抽真空是为了减少内外胆之间的气体介质,以减少其对流换热的作用。如果密闭性破坏,空气进入 两层夹缝中形成了内外胆之间的对流传热,从而保温瓶的保温效果降低。 导热 1-9一砖墙的表面积为12m,厚为260mm,平均导热系数为1.5WW(m.K)。设面向室内的表面温 度为25℃,而外表面温度为-5℃,试确定次砖墙向外界散失的热量。 解:根据傅立叶定律有: ④=1A =1.5×12×25-(-)5 △t =2076.9W 0.26 1-10一炉子的炉墙厚13cm,总面积为20m,平均导热系数为1.04wm.k,内外壁温分别是520℃ 及50℃。试计算通过炉墙的热损失。如果所燃用的煤的发热量是 2.09×104kJ/kg,问每天因热损失 要用掉多少千克煤? 解:根据傅利叶公式 Q=7AAt_1.04×20x(520-50)=75.2KW d 0.13 每天用煤 24×3600×75.2 =310.9Kg/d 2.09×104 1-11夏天,阳光照耀在一厚度为40m的用层压板制成的木门外表面上,用热流计测得木门内表面 热流密度为15Wm2。外变面温度为40℃,内表面温度为30℃。试估算此木门在厚度方向上的导热 系数。 q=入 4元=98_15x0.04 =0.06W/(m.K) 解: △t40-30 1-12在一次测定空气横向流过单根圆管的对流换热实验中,得到下列数据:管壁平均温度 tw=69℃, 空气温度t=20℃,管子外径d=14mm,加热段长80mm,输入加热段的功率8.5w,如果全部热量 通过对流换热传给空气,试问此时的对流换热表面传热系数多大? 解:根据牛顿冷却公式 q=2πrlh(tw-tf) q h=- 所以 dtw-ti)=49.33W1m.k) 1-13对置于水中的不锈钢束采用电加热的方法进行压力为 1.013×10Pa的饱和水沸腾换热实验。 测得加热功率为50W,不锈钢管束外径为4mm,加热段长10mm,表面平均温度为109℃。试计算 此时沸腾换热的表面传热系数。 解:根据牛顿冷却公式有 Φ=Ah△t h=Φ/ 7A4t=442.2 2 W/(m .K) 1-14一长宽各为10mm的等温集成电路芯片安装在一块地板上, 温度为20℃的空气在风扇作用下冷 却芯片。芯片最高允许温度为85℃,芯片与冷却气流间的表面传热系数为 175W1(m2.K。试确定在 不考虑辐射时芯片最大允许功率时多少?芯片顶面高出底板的高度为 1mm。 解:中x=hA4t=175W1m2.K水6.01×0.01+4×(0.01×0.001k(85C-20C) =1.5925W 1-15用均匀的绕在圆管外表面上的电阻带作加热元件,以进行管内流体对流换热的实验,如附图所 【第3页共284页】
【第 3 页 共 284 页】 1-8 热水瓶胆剖面的示意图如附图所示。瓶胆的两层玻璃之间抽成真空,内胆外壁及外胆内壁涂了 反射率很低的银。 试分析热水瓶具有保温作用的原因。 如果不小心破坏了瓶胆上抽气口处的密闭性, 这会影响保温效果吗? 解:保温作用的原因:内胆外壁外胆内壁涂了反射率很低的银,则通过内外胆向外辐射的热量很少, 抽真空是为了减少内外胆之间的气体介质,以减少其对流换热的作用。如果密闭性破坏,空气进入 两层夹缝中形成了内外胆之间的对流传热,从而保温瓶的保温效果降低。 导热 1-9 一砖墙的表面积为 12 2 m ,厚为 260mm,平均导热系数为 1.5W/ (m.K)。设面向室内的表面温 度为 25℃,而外表面温度为 -5℃,试确定次砖墙向外界散失的热量。 解: 根据傅立叶定律有: W t A 2076.9 0.26 25 ( )5 1.5 12 1-10 一炉子的炉墙厚 13cm,总面积为 20 2 m ,平均导热系数为 1.04w/m.k ,内外壁温分别是 520℃ 及 50℃。试计算通过炉墙的热损失。如果所燃用的煤的发热量是 2.09×104kJ/kg,问每天因热损失 要用掉多少千克煤? 解: 根据傅利叶公式 KW A t Q 75.2 0.13 1.04 20 (520 50) 每天用煤 310.9Kg / d 2.09 10 24 3600 75.2 4 1-11 夏天,阳光照耀在一厚度为 40mm 的用层压板制成的木门外表面上,用热流计测得木门内表面 热流密度为 15W/m 2。外变面温度为 40℃,内表面温度为 30℃。试估算此木门在厚度方向上的导热 系数。 解: t q , 0.06 /( . ) 40 30 15 0.04 W m K t q 1-12 在一次测定空气横向流过单根圆管的对流换热实验中,得到下列数据:管壁平均温度 t w=69℃, 空气温度 tf=20℃,管子外径 d=14mm,加热段长 80mm,输入加热段的功率 8.5w,如果全部热量 通过对流换热传给空气,试问此时的对流换热表面传热系数多大? 解: 根据牛顿冷却公式 q 2 rlh tw t f 所以 w f d t t q h =49.33W/(m 2 .k) 1-13 对置于水中的不锈钢束采用电加热的方法进行压力为 1.013 Pa 5 10 的饱和水沸腾换热实验。 测得加热功率为 50W,不锈钢管束外径为 4mm,加热段长 10mm,表面平均温度为 109℃。试计算 此时沸腾换热的表面传热系数。 解: 根据牛顿冷却公式有 Ah t 4 4 2.23 A t h W/(m 2 .K) 1-14 一长宽各为 10mm 的等温集成电路芯片安装在一块地板上, 温度为 20℃的空气在风扇作用下冷 却芯片。 芯片最高允许温度为 85℃,芯片与冷却气流间的表面传热系数为 175 W/(m 2 .K) 。试确定在 不考虑辐射时芯片最大允许功率时多少?芯片顶面高出底板的高度为 1mm。 解: 175 / . 0.01 0.01 4 0.01 0.001 2 max hA t W m K (85℃-20℃ ) = 1.5925W 1-15 用均匀的绕在圆管外表面上的电阻带作加热元件,以进行管内流体对流换热的实验,如附图所

示。用功率表测得外表面加热的热流密度为 3500WWm:用热电偶测得某一截面上的空气温度为 45℃,内管壁温度为80℃。设热量沿径向传递,外表面绝热良好,试计算所讨论截面上的局部表面 传热系数。圆管的外径为36mm,壁厚为2mm。 解:由题意3500Wm×2πRl=h×2m×(80℃-45℃) 又r=R-δ=(18-2)mm=16mm ÷h=112.5wm2M 1-16为了说明冬天空气的温度以及风速对人体冷暖感觉的影响,欧美国家的天气预报中普遍采用风 冷温度的概念(wind-chill temperature)。风冷温度是一个当量的环境温度,当人处于静止空气的风冷 温度下时其散热量与人处于实际气温、实际风速下的散热量相同。从散热计算的角度可以将人体简 化为直径为25cm、高175cm、表面温度为30℃的圆柱体,试计算当表面传热系数为15W1m2K时 人体在温度为20℃的静止空气中的散热量。如果在一个有风的日子,表面传热系数增加到 50W1m2K)人体的散热量又是多少?此时风冷温度是多少? 辐射 1-17有两块无限靠近的黑体平行平板,温度分别为T,T2。试按黑体的性质及斯藩一玻尔兹曼定律导 出单位面积上辐射换热量的计算式。(提示:无限靠近意味着每一块板发出的辐射能全部落到另一块 板上。) 解:由题意 qit =GT1:qat =GT2 两板的换热量为 q=o(T1-T2) 1-18宇宙空间可近似地看成为0K的真空空间。一航天器在太空中飞行,其外表面平均温度为250℃, 表面发射率为0.7,试计算航天器单位表面上的换热量。 解: q=8oT4-0.7×5.67×10W1(m2.K)×250=155wm2 1-19在1-14题目中,如果把芯片及底板置于一个封闭的机壳内,机壳的平均温度为 20℃,芯片的 表面黑度为0.9,其余条件不变,试确定芯片的最大允许功率。 解: Φ射=Ao(T,4-T24于0.9×5.67×108[(85+273)-(20+273)4]×0.00014 p中对流十中时=1.657W 1-20半径为0.5的球状航天器在太空中飞行,其表面发射率为0.8。航天器内电子元件的散热总共 为175W。假设航天器没有从宇宙空间接受任何辐射能量,试估算其表面的平均温度。 解:电子原件的发热量=航天器的辐射散热量即: Q=80T4 Q :.T=1sGA =187K 热阻分析 1-21有一台气体冷却器,气侧表面传热系数h=95wWm2N,壁面厚6=2.5mm, 2=46.5W1(m.K)水侧表面传热系数h2=5800WIm2.KN。设传热壁可以看成平壁,试计算各个 环节单位面积的热阻及从气到水的总传热系数。你能否指出,为了强化这一传热过程,应首先从哪 一环节着手? R=1=0.010526:R2= 解: h _0025-5376×10,R-150-1.724*10-, 246.5 h25800 K=1+1+8 则h,h2=94.7W(m2.K),应强化气体侧表面传热。 【第4页共284页】
【第 4 页 共 284 页】 示。用功率表测得外表面加热的热流密度为 3500W/ 2 m ;用热电偶测得某一截面上的空气温度为 45℃,内管壁温度为 80℃。设热量沿径向传递,外表面绝热良好,试计算所讨论截面上的局部表面 传热系数。圆管的外径为 36mm,壁厚为 2mm。 解: 由题意 3500W/ m 2 Rl h 2 rl 2 (80℃-45℃) 又 r= R =(18-2)mm=16mm h 112.5 W/(m 2 .K) 1-16 为了说明冬天空气的温度以及风速对人体冷暖感觉的影响,欧美国家的天气预报中普遍采用风 冷温度的概念 (wind-chill temperature )。风冷温度是一个当量的环境温度, 当人处于静止空气的风冷 温度下时其散热量与人处于实际气温、实际风速下的散热量相同。从散热计算的角度可以将人体简 化为直径为 25cm、高 175cm、表面温度为 30℃的圆柱体,试计算当表面传热系数为 W m K 2 15 / 时 人体在温度为 20℃的静止空气中的散热量。如果在一个有风的日子,表面传热系数增加到 W m K 2 50 / ,人体的散热量又是多少?此时风冷温度是多少? 辐射 1-17 有两块无限靠近的黑体平行平板,温度分别为 1 2 T ,T 。试按黑体的性质及斯藩 -玻尔兹曼定律导 出单位面积上辐射换热量的计算式。 (提示: 无限靠近意味着每一块板发出的辐射能全部落到另一块 板上。) 解: 由题意 4 q1f T1 ; 4 q2 f T2 ; 两板的换热量为 ( ) 4 2 4 q T1 T 1-18 宇宙空间可近似地看成为 0K 的真空空间。 一航天器在太空中飞行, 其外表面平均温度为 250℃, 表面发射率为 0.7,试计算航天器单位表面上的换热量。 解: 4 q T =0.7 5.67 10 /( . ) 250 155 8 2 4 4 W m K W/ 2 m 1-19 在 1-14 题目中,如果把芯片及底板置于一个封闭的机壳内,机壳的平均温度为 20℃,芯片的 表面黑度为 0.9,其余条件不变,试确定芯片的最大允许功率。 解: 0.9 5.67 10 [(85 273) (20 273) ] 0.00014 4 8 4 4 2 4 辐射 A T1 T = P 对流+ 辐射 =1.657W 1-20 半径为 0.5 m 的球状航天器在太空中飞行, 其表面发射率为 0.8。航天器内电子元件的散热总共 为 175W。假设航天器没有从宇宙空间接受任何辐射能量,试估算其表面的平均温度。 解: 电子原件的发热量=航天器的辐射散热量即: 4 Q T 4 A Q T =187K 热阻分析 1-21 有 一 台 气 体 冷 却 器 , 气 侧 表 面 传 热 系 数 h1 = 95W/(m 2 .K) , 壁 面 厚 = 2.5mm , 46.5W /( m.K ) 水侧表面传热系数 h2 5800W/(m 2 .K)。设传热壁可以看成平壁,试计算各个 环节单位面积的热阻及从气到水的总传热系数。你能否指出,为了强化这一传热过程,应首先从哪 一环节着手? 解: 0.010526; 1 1 1 h R 5.376 10 ; 46.5 0.0025 5 R2 1.724 10 ; 5800 1 1 4 2 3 h R 则 1 2 1 1 1 h h K =94.7 /( . ) 2 W m K ,应强化气体侧表面传热
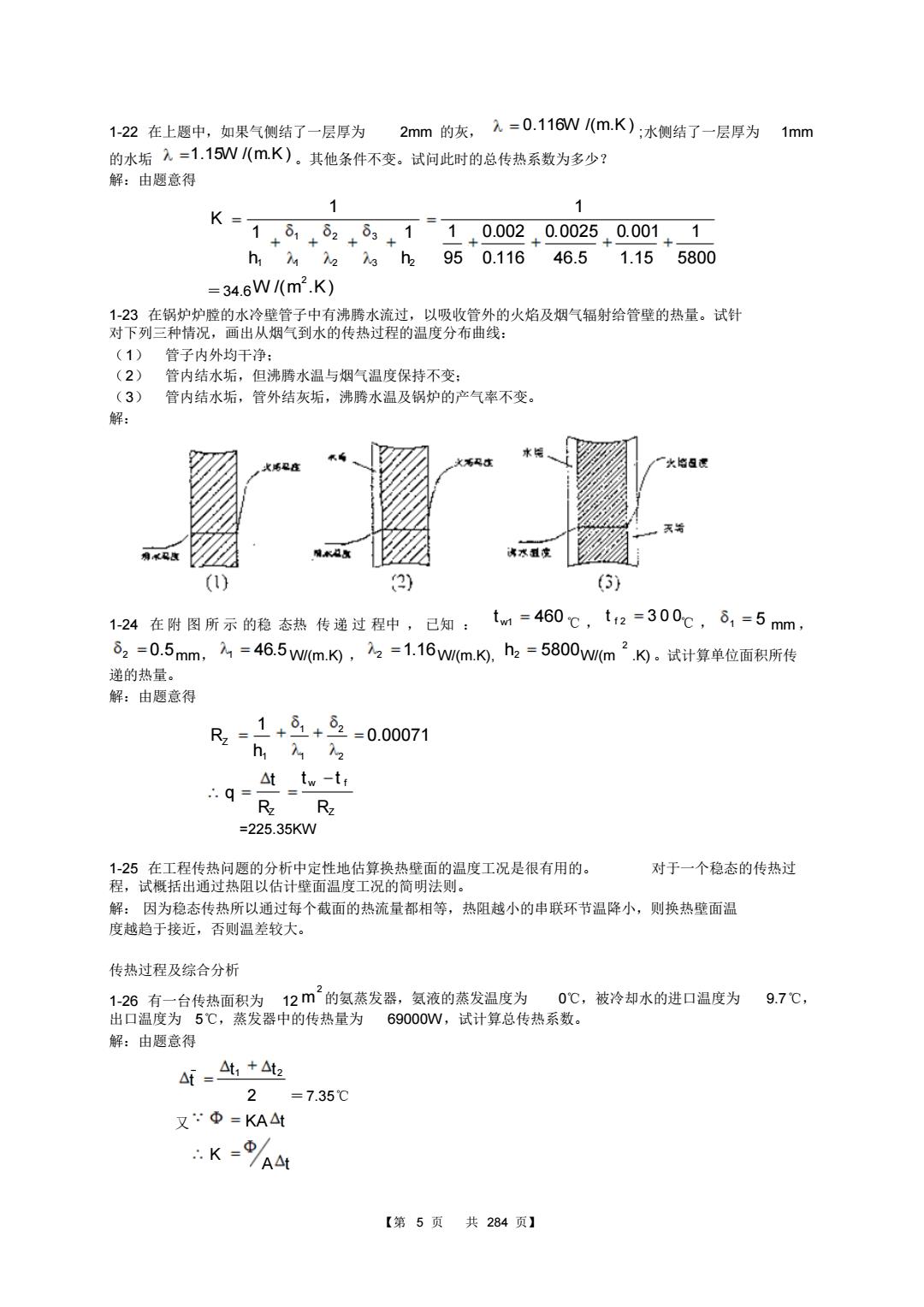
1-22在上题中,如果气侧结了一层厚为2mm的灰,元=0.116W(m.K):水侧结了一层厚为1mm 的水垢入=1.15W(m.K)。其他条件不变。试问此时的总传热系数为多少? 解:由题意得 1 1 K= 1+8,+82+8+1 1+0.002+0.0025+0.001+1 h1742273h2950.11646.51.155800 =34.6W1(m2.K) 1-23在锅炉炉膛的水冷壁管子中有沸腾水流过,以吸收管外的火焰及烟气辐射给管壁的热量。试针 对下列三种情况,画出从烟气到水的传热过程的温度分布曲线: (1)管子内外均千净: (2)管内结水垢,但沸腾水温与烟气温度保持不变: (3) 管内结水垢,管外结灰垢,沸腾水温及锅炉的产气率不变。 解: 火且度 滑不只点 (1) 2) (3) 1-24在附图所示的稳态热传递过程中,已知:t,=460℃,t12=300℃,81=5mm, δ2=0.5mm,7=46.5wm.K),72=1.16wmN,h2=5800Wm2)。试计算单位面积所传 递的热量。 解:由题意得 R,=1+8+82=0.00071 h12 △ttw-ti R RZ =225.35KW 1-25在工程传热问题的分析中定性地估算换热壁面的温度工况是很有用的。 对于一个稳态的传热过 程,试概括出通过热阻以估计壁面温度工况的简明法则。 解:因为稳态传热所以通过每个截面的热流量都相等,热阻越小的串联环节温降小,则换热壁面温 度越趋于接近,否则温差较大。 传热过程及综合分析 1-26有一台传热面积为12m的氨蒸发器,氨液的蒸发温度为0℃,被冷却水的进口温度为9.7℃, 出口温度为5℃,蒸发器中的传热量为69000W,试计算总传热系数。 解:由题意得 4f=4t,+42 2 =7.35℃ 又Φ=KA△t K-/ /A△t 【第5页共284页】
【第 5 页 共 284 页】 1-22 在上题中,如果气侧结了一层厚为 2mm 的灰, 0.116W /(m.K ) ;水侧结了一层厚为 1mm 的水垢 1.15W /(m.K ) 。其他条件不变。试问此时的总传热系数为多少? 解:由题意得 5800 1 1.15 0.001 46.5 0.0025 0.116 0.002 95 1 1 1 1 1 3 2 3 2 2 1 1 h1 h K =34.6 /( . ) 2 W m K 1-23 在锅炉炉膛的水冷壁管子中有沸腾水流过,以吸收管外的火焰及烟气辐射给管壁的热量。试针 对下列三种情况,画出从烟气到水的传热过程的温度分布曲线: (1) 管子内外均干净; (2) 管内结水垢,但沸腾水温与烟气温度保持不变; (3) 管内结水垢,管外结灰垢,沸腾水温及锅炉的产气率不变。 解: 1-24 在 附 图 所 示 的稳 态热 传 递 过 程中 , 已知 : t w1 460 ℃ , t f 2 3 0 0℃ , 1 5 mm , 2 0.5mm, 1 46.5 W/(m.K) , 2 1.16W/(m.K), h2 5800W/(m 2 .K) 。试计算单位面积所传 递的热量。 解:由题意得 0.00071 1 2 2 1 1 h1 RZ Z w f Z R t t R t q =225.35KW 1-25 在工程传热问题的分析中定性地估算换热壁面的温度工况是很有用的。 对于一个稳态的传热过 程,试概括出通过热阻以估计壁面温度工况的简明法则。 解: 因为稳态传热所以通过每个截面的热流量都相等,热阻越小的串联环节温降小,则换热壁面温 度越趋于接近,否则温差较大。 传热过程及综合分析 1-26 有一台传热面积为 12 2 m 的氨蒸发器,氨液的蒸发温度为 0℃,被冷却水的进口温度为 9.7℃, 出口温度为 5℃,蒸发器中的传热量为 69000W,试计算总传热系数。 解:由题意得 2 t1 t2 t =7.35℃ 又 KA t A t K

=782.3W/m2.K) 1-27设冬天室内的温度为t1,室外温度为t12,试在该两温度保持不变的条件下,画出下列三种情 形从室内空气到室外大气温度分布的示意性曲线: (1)室外平静无风: (2)室外冷空气以一定流速吹过砖墙表面: (3)除了室外刮风以外,还要考虑砖墙与四周环境间的辐射换热。 解 tii t2- 1-28对于图1-4所示的穿过平壁的传热过程,试分析下列情形下温度曲线的变化趋向: (1) δ/2→0:(2)h1→0:(3)h2→0。 f 2 1-29在上题所述的传热过程中,假设 δ/入=0,试计算下列情形中分隔壁的温度:(1)h=h2: (2)h=2h2;(3)h=0.5h。 解:入 =0:∴.tM=tw2 又Ah,twi-tf2)=Ah2tw2-tf2)】 h=h时n=t2=,t2 tw =tw2 2t1+t12 (2)h=2h时 3 《3)h=05n时m=te-tnt2e 3 1-30设图1-4所示壁面两侧分别维持在20℃及0℃,且高温侧受到流体的加热, δ=0.08m,t1=100°C,h,=200W(m.K),过程是稳态的,试确定壁面材料的导热系数。 g.g=hin-t上若tu-te) 元-hδt,-tm) tw-tw2 【第6页共284页】
【第 6 页 共 284 页】 =782.3 /( . ) 2 W m K 1-27 设冬天室内的温度为 f1 t ,室外温度为 f 2 t ,试在该两温度保持不变的条件下,画出下列三种情 形从室内空气到室外大气温度分布的示意性曲线: (1)室外平静无风; (2)室外冷空气以一定流速吹过砖墙表面; (3)除了室外刮风以外,还要考虑砖墙与四周环境间的辐射换热。 解 1-28 对于图 1-4 所示的穿过平壁的传热过程,试分析下列情形下温度曲线的变化趋向: ( 1) / 0 ;(2) h1 ;(3) h2 。 1-29 在上题所述的传热过程中,假设 / 0 ,试计算下列情形中分隔壁的温度: ( 1) h1 h2; (2) h1 2h2 ;(3)h1 0.5h2 。 解: 1 2 0; t w t w 又 Ah1 t w1 t f 2 Ah2 t w2 t f 2 (1)h1 h2 时 2 1 2 1 2 f f w w t t t t (2) h1 2h2 时 3 2 1 2 1 2 f f w w t t t t (3) h1 0.5h2 时 3 1 2 2 1 2 f f w w t t t t 1-30 设 图 1-4 所 示 壁 面 两 侧 分 别 维 持 在 20 ℃ 及 0 ℃ , 且 高 温 侧 受 到 流 体 的 加 热 , 0.08 , 100 , 200 /( . ) 2 1 0 m t f 1 C h W m K ,过程是稳态的,试确定壁面材料的导热系数。 解: 1 f 1 w1 w1 w2 q h t t t t 1 2 1 1 1 w w f w t t h t t t f 1 t f 2 f 1 t f 2 t

=64W1(m.K) 1-31附图所示的空腔由两个平行黑体表面组成,空腔内抽成真空,且空腔的厚度远小于其高度与宽 度。其余已知条件如图示。表面2是厚为8=0.1的平板的一侧面,其另一侧表面3被高温流体加 热,平板的导热系数入=17.5W(m.K)。试问在稳态工况下表面3的温度t8为多少? Atwo-tw2 =A() 解:在稳态工况下因为 G(Tw2-Tw) ∴.tw3= +tw2 =132.67℃ 1-32一玻璃窗,尺寸为60cm×30cm,厚为4mm。冬天,室内及室外温度分别为20℃及-20℃, 内表面的自然对流换热表面系数为W,外表面强制对流换热表面系数为 50W(m.K)。玻璃的导热 系数入=0.78W1(m.K)。试确定通过玻璃的热损失。 △T 币三 1 +1+ 解: hA Ah2 A) =57.5W 1-33一个储存水果的房间的墙用软木板做成,厚为200mm,其中一面墙的高与宽各为3m及6m。 冬天设室内温度为2C,室外为-10℃,室内墙壁与环境之间的表面传热系数为6W(mK),室外刮 强风时的表面传热系数为60W(mK)。软木的导热系数元=0.044W(mK)。试计算通过这面墙 所散失的热量,并讨论室外风力减弱对墙散热量的影响(提示:可以取室外的表面传热系数值为原 来的二分之一或四分之一来估算) 解:由题意 Φ= T 1 +1 hw1 A Ahw A入 =45.67W hw =30 w/(m .K) 2 当室外风力减弱时 △T Φ= 1+1 hN1 A Ahw A元=45.52W 单位换算 1-34.一台R22的空调器的冷凝器如附图所示。温度为313K的氟利昂22的饱和蒸气在管子内流动, 温度为283K的空气进入冷凝器冷却氟利昂蒸气使其凝结。该冷凝器的迎风面积为 0.4m,迎面风 速为2/S。氟利昂蒸气的流量为0.011kg/s,从凝结氟利昂蒸气到空气的总传热系数为 40W1mK)试确定该冷凝器所需的传热面积。提示:以空气进、出口温度的平均值作为计算传热 温差的空气温度。所谓迎风面积是指空气进入冷凝器之前的流动面积。 1-35.一战车的齿轮箱外表面积为0.2m,为安全需要,其最高温度不超过65℃,为此用25℃的冷空 气强制对流流过此表面。该齿轮箱在稳态运行时消耗的机械能为 1000W。假定这份能量全部通过对 流传热散失到环境中,所需的对流传热系数应多大?如果齿轮箱四周的固体表面平均温度为 30℃, 试分析通过辐射传热最多可以带走多少热量?齿轮箱表明的发射率可取为 0.85。 解: 1-36.航空喷气发动机的工作叶片与高温的燃气相接触,为了使叶片金属的温度不超过允许数值,常 【第7页共284页】
【第 7 页 共 284 页】 =64W /(m.K ) 1-31 附图所示的空腔由两个平行黑体表面组成,空腔内抽成真空,且空腔的厚度远小于其高度与宽 度。其余已知条件如图示。表面 2 是厚为 0.1m 的平板的一侧面,其另一侧表面 3 被高温流体加 热,平板的导热系数 17.5W /(m.K )。试问在稳态工况下表面 3 的温度 w3 t 为多少? 解:在稳态工况下因为 4 1 4 2 3 2 w w w w A T T t t A 2 4 1 4 2 3 w w w w t T T t =132.67℃ 1-32 一玻璃窗,尺寸为 60 cm 30cm,厚为 4 mm。冬天,室内及室外温度分别为 20℃及 -20℃, 内表面的自然对流换热表面系数为 W,外表面强制对流换热表面系数为 50W /(m.K) 。玻璃的导热 系数 0.78W /(m.K )。试确定通过玻璃的热损失。 解: h A Ah A T 1 2 1 1 =57.5W 1-33 一个储存水果的房间的墙用软木板做成, 厚为 200 mm,其中一面墙的高与宽各为 3 m 及 6 m。 冬天设室内温度为 2℃,室外为 -10℃,室内墙壁与环境之间的 表面传热系数为 6W /(m.K ) ,室外刮 强风时的表面传热系数为 60W /( m.K ) 。软木的导热系数 0.044W /(m.K ) 。试计算通过这面墙 所散失的热量,并讨论室外风力减弱对墙散热量的影响(提示:可以取室外的表面传热系数值为原 来的二分之一或四分之一来估算) 。 解:由题意 h A Ah A T N W 1 1 1 =45.67W 当室外风力减弱时 hW 30 W/(m 2 .K) h A Ah A T N W 1 1 1 =45.52W 单位换算 1-34.一台 R22 的空调器的冷凝器如附图所示。 温度为 313K 的氟利昂 22 的饱和蒸气在管子内流动, 温度为 283K 的空气进入冷凝器冷却氟利昂蒸气使其凝结。该冷凝器的迎风面积为 2 0.4m ,迎面风 速 为 2m / s 。 氟 利 昂蒸 气 的 流量 为 0.011kg / s , 从 凝 结氟 利 昂 蒸气 到 空 气 的 总传 热 系数为 W m K 2 40 / ,试确定该冷凝器所需的传热面积。提示:以空气进、出口温度的平均值作为计算传热 温差的空气温度。所谓迎风面积是指空气进入冷凝器之前的流动面积。 1-35.一战车的齿轮箱外表面积为 0.2 ㎡,为安全需要,其最高温度不超过 65℃,为此用 25℃的冷空 气强制对流流过此表面。该齿轮箱在稳态运行时消耗的机械能为 1000W。假定这份能量全部通过对 流传热散失到环境中,所需的对流传热系数应多大?如果齿轮箱四周的固体表面平均温度为 30℃, 试分析通过辐射传热最多可以带走多少热量?齿轮箱表明的发射率可取为 0.85。 解: 1-36.航空喷气发动机的工作叶片与高温的燃气相接触,为了使叶片金属的温度不超过允许数值,常

在叶片中间铸造出冷却通道,从压气机出口抽出一小部分冷空气进入这些通道。附图中示意性地画 出了这样的叶片的截面。现在给出以下数据:空心叶片内表面面积A=200mm2,冷却空气的平均温 度t=700℃,表面传热系数h=320W(m2*K:面积A=2840mm2的叶片外表面与平均温度为1000℃ 的燃气接触,平均表面传热系数h=1420W(m2*K)。此时叶片外表面温度为820℃,内表面温度为 790℃。试分析此时该叶片内的导热是否处于稳态? 解: 1-37.一宇航员在太空模拟舱内工作(检测仪器仪表的工作性能),该模拟舱外表面面积为3㎡,外表 面温度为0℃,表面发射率为0.05。模拟舱位于表面温度为-100℃的人工环境的大壳体内。此时模拟 舱内的温度保持恒定,试确定模拟舱表面的辐射散热量。这份能量都是有宇航员身上散失的吗? 解: 1-38.在例题1-6中,为获得1h后该男子的体温平均下降的数值,可以近似地认为他向环境的散热量 为一常数。实际上,这一散热量是随时间而变化的。(1)分析该男子向环境散热的方式:(2)如何 计算其辐射传热量随时间的变化,并估算考虑这一变化后1内的辐射总散热量,皮肤与衣料的表面 发射率可取为0.9,刚开始时平均表面温度为31℃,环境为10℃:(3)如何计算其向四周冷空气的 对流传热量随时间的变化,并估算考虑这一变化后h内的对流总散热量。由于人体的颤抖,人体向 冷空气散热的对流传热表面传热系数可取为 20WW(m·K灯。该男子的散热面积可以用直径为0.318cm、 高1.7m的圆柱体的面积来近似代替。 解: 1-39当空气与壁面的平均温度在30~50℃范围时,空气在水平管外自然对流的 表面传热系数可按 下列式计算: h=C(At/d)4 式中:常量C=1.04kcal(m5hC125):直径d的单位为m温差t的单位为℃,h的单位为 kcal/(m.h.℃)。试用我国法定计量单位写出此公式。 解: 1-40对于水在大容器内的饱和沸腾试验,有人提出了下列经验公式: h=C2(p14+C,p2)g07 式中:C,=9.339×10“m12/N189,C2=0.628W03(K.m2.N01):其他各量的单位为 p-NIm,q-WIm,h-W(mK)。试将此式改用工程单位制单位写出。 第二章 思考题 1试写出导热傅里叶定律的一般形式,并说明其中各个符号的意义。 d q=-gradt=-入 答:傅立叶定律的一般形式为: x",其中:gradt为空间某点的温度梯度:n 是通过该点的等温线上的法向单位矢量,指向温度升高的方向: q为该处的热流密度矢量。 2已知导热物体中某点在x,y,z三个方向上的热流密度分别为 qx,qy及qz,如何获得该点的 热密度 矢量? 答: q=qxi+qyj+qzk,其中i,j,k分别为三个方向的单位矢量量。 3试说明得出导热微分方程所依据的基本定律。 答:导热微分方程式所依据的基本定律有:傅立叶定律和能量守恒定律。 【第8页共284页】
【第 8 页 共 284 页】 在叶片中间铸造出冷却通道,从压气机出口抽出一小部分冷空气进入这些通道。附图中示意性地画 出了这样的叶片的截面。现在给出以下数据:空心叶片内表面面积 A i=200mm 2,冷却空气的平均温 度 tfi=700℃,表面传热系数 hi=320W/(m 2 *K) ;面积 Ao=2840mm2的叶片外表面与平均温度为 1000℃ 的燃气接触,平均表面传热系数 ho=1420W/(m 2 *K) 。此时叶片外表面温度为 820℃,内表面温度为 790℃。试分析此时该叶片内的导热是否处于稳态? 解: 1-37.一宇航员在太空模拟舱内工作 (检测仪器仪表的工作性能) ,该模拟舱外表面面积为 3 ㎡,外表 面温度为 0℃,表面发射率为 0.05。模拟舱位于表面温度为 -100℃的人工环境的大壳体内。 此时模拟 舱内的温度保持恒定,试确定模拟舱表面的辐射散热量。这份能量都是有宇航员身上散失的吗? 解: 1-38.在例题 1-6 中,为获得 1h 后该男子的体温平均下降的数值,可以近似地认为他向环境的散热量 为一常数。实际上,这一散热量是随时间而变化的。 (1)分析该男子向环境散热的方式; (2)如何 计算其辐射传热量随时间的变化, 并估算考虑这一变化后 1h 内的辐射总散热量, 皮肤与衣料的表面 发射率可取为 0.9,刚开始时平均表面温度为 31℃,环境为 10℃;(3)如何计算其向四周冷空气的 对流传热量随时间的变化,并估算考虑这一变化后 1h 内的对流总散热量。由于人体的颤抖,人体向 冷空气散热的对流传热表面传热系数可取为 20W/( ㎡·K)。该男子的散热面积可以用直径为 0.318cm、 高 1.7m 的圆柱体的面积来近似代替。 解: 1-39 当空气与壁面的平均温度在 30~50℃范围时,空气在水平管外自然对流的 表面传热系数可按 下列式计算: 1/ 4 h C( t / d) 式中:常量 1.04 /( . . ) 1.75 1.25 C kcal m h C ;直径 d 的单位为 m;温差 t 的单位为℃, h 的单位为 /( . . ) 2 kcal m h C 。试用我国法定计量单位写出此公式。 解: 1-40 对于水在大容器内的饱和沸腾试验,有人提出了下列经验公式: 2 0.7 1 0.14 2 h C ( p C p )q 式 中 : 14 1.72 1.86 1 C 9.339 10 m / N , 0.628 /( . . ) 0.3 0.32 0.14 C2 W K m N ; 其 他 各 量 的 单 位 为 p / , / , /( . ) 2 2 N m q W m h W mK 。试将此式改用工程单位制单位写出。 第二章 思考题 1 试写出导热傅里叶定律的一般形式,并说明其中各个符号的意义。 答:傅立叶定律的一般形式为: n x t q=- gradt ,其中: gradt 为空间某点的温度梯度; n 是通过该点的等温线上的法向单位矢量,指向温度升高的方向; q 为该处的热流密度矢量。 2 已知导热物体中某点在 x,y,z 三个方向上的热流密度分别为 qx q y , 及 qz ,如何获得该点的 热密度 矢量? 答: q qx i qy j qz k ,其中 i , j, k 分别为三个方向的单位矢量量。 3 试说明得出导热微分方程所依据的基本定律。 答: 导热微分方程式所依据的基本定律有:傅立叶定律和能量守恒定律

4试分别用数学语言将传热学术语说明导热问题三种类型的边界条件。 答:①第一类边界条件:t>0时,tw=f,() x>0时 ②第二类边界条件: -().=f,) CX -()w=htw-t) ③第三类边界条件: 5试说明串联热阻叠加原则的内容及其使用条件。 答:在一个串联的热量传递过程中,如果通过每个环节的热流量都相同,则各串联环节的总热阻等 于各串联环节热阻的和。使用条件是对于各个传热环节的传热面积必须相等。 7.通过圆筒壁的导热量仅与内、外半径之比有关而与半径的绝对值无关,而通过球壳的导热量计算 式却与半径的绝对值有关,怎样理解? 答:因为通过圆筒壁的导热热阻仅和圆筒壁的内外半径比值有关,而通过球壳的导热热阻却和 球壳的绝对直径有关,所以绝对半径不同时,导热量不一样。 6发生在一个短圆柱中的导热问题,在下列哪些情形下可以按一维问题来处理? 答:当采用圆柱坐标系,沿半径方向的导热就可以按一维问题来处理。 8扩展表面中的导热问题可以按一维问题来处理的条件是什么?有人认为,只要扩展表面细长,就 可按一维问题来处理,你同意这种观点吗? 答:只要满足等截面的直肋,就可按一维问题来处理。不同意,因为当扩展表面的截面不均时,不 同截面上的热流密度不均匀,不可看作一维问题。 9肋片高度增加引起两种效果:肋效率下降及散热表面积增加。因而有人认为,随着肋片高度的增 加会出现一个临界高度,超过这个高度后,肋片导热热数流量反而会下降。试分析这一观点的正确 性。 答:错误,因为当肋片高度达到一定值时,通过该处截面的热流密度为零。通过肋片的热流已达到 最大值,不会因为高度的增加而发生变化。 10在式(2-57)所给出的分析解中,不出现导热物体的导热系数,请你提供理论依据。 答:由于式(2-57)所描述的问题为稳态导热,且物体的导热系数沿 X方向和y方向的数值相等并 为常数。 11有人对二维矩形物体中的稳态无内热源常物性的导热问题进行了数值计算。矩形的一个边绝热, 其余三个边均与温度为【:的流体发生对流换热。你能预测他所得的温度场的解吗? 答:能,因为在一边绝热其余三边为相同边界条件时,矩形物体内部的温度分布应为关于绝热边的 中心线对称分布。 习题 平板 2-1用平底锅烧开水,与水相接触的锅底温度为111℃,热流密度为42400W/m。使用一段时间后, 锅底结了一层平均厚度为3mm的水垢。假设此时与水相接触的水垢的表面温度及热流密度分别等于 原来的值,试计算水垢与金属锅底接触面的温度。水垢的导热系数取为 1W/(m.。 解:由题意得 q== tw-111 =42400 0.003 7 w/m2 所以t=238.2℃ 2-2一冷藏室的墙由钢皮矿渣棉及石棉板三层叠合构成,各层的厚度依次为 0.794mm.,152mm及 9.5mm,导热系数分别为45W(mK),0.07W1(m.K)及0.1W(m.K)。冷藏室的有效换热面积为 37.2,室内外气温分别为-2℃及30℃,室内外壁面的表面传热系数可分别按 1.5W(m2.K)及 2.5W(mK)计算。为维持冷藏室温度恒定,试确定冷藏室内的冷却排管每小时需带走的热量。 【第9页共284页】
【第 9 页 共 284 页】 4 试分别用数学语言将传热学术语说明导热问题三种类型的边界条件。 答: ① 第一类边界条件: 0 ( ) 1 时, t w f ② 第二类边界条件: 0 ( ) ( ) 2 f x t 时 w ③ 第三类边界条件: ( ) ( ) w w f h t t x t 5 试说明串联热阻叠加原则的内容及其使用条件。 答: 在一个串联的热量传递过程中,如果通过每个环节的热流量都相同,则各串联环节的总热阻等 于各串联环节热阻的和。使用条件是对于各个传热环节的传热面积必须相等。 7.通过圆筒壁的导热量仅与内、外半径之比有关而与半径的绝对值无关,而通过球壳的导热量计算 式却与半径的绝对值有关,怎样理解? 答:因为通过圆筒壁的导热热阻仅和圆筒壁的内外半径比值有关,而通过球壳的导热热阻却和 球壳的绝对直径有关,所以绝对半径不同时,导热量不一样。 6 发生在一个短圆柱中的导热问题,在下列哪些情形下可以按一维问题来处理? 答: 当采用圆柱坐标系,沿半径方向的导热就可以按一维问题来处理。 8 扩展表面中的导热问题可以按一维问题来处理的条件是什么?有人认为,只要扩展表面细长,就 可按一维问题来处理,你同意这种观点吗? 答: 只要满足等截面的直肋,就可按一维问题来处理。不同意,因为当扩展表面的截面不均时,不 同截面上的热流密度不均匀,不可看作一维问题。 9 肋片高度增加引起两种效果:肋效率下降及散热表面积增加。因而有人认为,随着肋片高度的增 加会出现一个临界高度,超过这个高度后,肋片导热热数流量反而会下降。试分析这一观点的正确 性。 答: 错误,因为当肋片高度达到一定值时,通过该处截面的热流密度为零。通过肋片的热流已达到 最大值,不会因为高度的增加而发生变化。 10 在式( 2-57)所给出的分析解中,不出现导热物体的导热系数,请你提供理论依据。 答: 由于式( 2-57)所描述的问题为稳态导热,且物体的导热系数沿 x 方向和 y 方向的数值相等并 为常数。 11 有人对二维矩形物体中的稳态无内热源常物性的导热问题进行了数值计算。矩形的一个边绝热, 其余三个边均与温度为 f t 的流体发生对流换热。你能预测他所得的温度场的解吗? 答: 能,因为在一边绝热其余三边为相同边界条件时,矩形物体内部的温度分布应为关于绝热边的 中心线对称分布。 习题 平板 2-1 用平底锅烧开水, 与水相接触的锅底温度为 111℃,热流密度为 42400 2 W / m 。使用一段时间后, 锅底结了一层平均厚度为 3mm 的水垢。假设此时与水相接触的水垢的表面温度及热流密度分别等于 原来的值,试计算水垢与金属锅底接触面的温度。水垢的导热系数取为 1W/(m.K) 。 解: 由题意得 42400 1 0.003 tw 111 q = w/m 2 所以 t=238.2℃ 2-2 一冷藏室的墙由钢皮矿渣棉及石棉板三层叠合构成,各层的厚度依次为 0.794mm.,152mm 及 9.5mm,导热系数分别为 45W /( m.K ) ,0. 07W /(m.K ) 及 0.1W /(m.K ) 。冷藏室的有效换热面积为 37.2 2 m ,室内外气温分别为 -2℃及 30℃,室内外壁面的表面传热系数可分别按 1.5 /( . ) 2 W m K 及 2.5 /( . ) 2 W m K 计算。为维持冷藏室温度恒定,试确定冷藏室内的冷却排管每小时需带走的热量

解:由题意得 Φ=A× ti-t2 30-(-2) 1+1+8+2+δ91+1+0.000794+0.152+0.0095 ×37.2 h1h242a=1.52.5 45 0.07 0.1 =357.14W 357.14×3600=1285.6KJ 2-3有一厚为20mm的平板墙,导热系数为1.3W(m.K)。为使每平方米墙的热损失不超过 1500W, 在外表面上覆盖了一层导热系数为0.12W(m.K)的保温材料。已知复合壁两侧的温度分别为750℃ 及55℃,试确定此时保温层的厚度。 解:依据题意,有 t1-t2750-55 q= ≤1500 8,+δ20.020+62 421.30.12 ,解得:δ2≥0.05375m 24一烘箱的炉门由两种保温材料A及B组成,且δA=2δ。(见附图)。已知 A=0.W(m.K),e=0.06W(mK),烘箱内空气温度t1=400℃,内壁面的总表面传热系数 h=50W(m.K)。为安全起见,希望烘箱炉门的外表面温度不得高于50℃。设可把炉门导热作为 一维问题处理,试决定所需保温材料的厚度。环境温度t12=25℃,外表面总传热系数 h2=9.5W1(m2.K). tu-tw=m(tn-t)+h(t-t:2) q=8+8B 解:热损失为 XA B 又tw=50℃:δA=δB 联立得δa=0.078mδ。=0.039m 2-5对于无限大平板内的一维导热问题,试说明在三类边界条件中,两侧边界条件的哪些组合可以 使平板中的温度场获得确定的解? 解:两侧面的第一类边界条件:一侧面的第一类边界条件和第二类边界条件:一侧面的第一类边界 条件和另一侧面的第三类边界条件:一侧面的第一类边界条件和另一侧面的第三类边界条件。 平壁导热 2-6一火箭发动机燃烧室是直径为130mm的圆筒体,厚2.1mm,导热系数为23.2WW(m·K灯。圆筒壁 外用液体冷却,外壁温度为240℃。测得圆筒体的热流密度为4.8×10°WMm,其材料的最高允许温 度为700℃。试判断该燃烧室壁面是否工作于安全温度范围内? 解: 2-7如附图所示的不锈钢平底锅置于电器灶具上被加热,灶具的功率为 1000W,其中85%用于加热 平底锅。锅底厚8=3m,平底部分直径d=200mm,不锈刚的导热系数入=18W(m·K),锅内汤料 与锅底的对流传热表面传热系数为 2500W(m·K),流体平均温度t=95℃。试列出锅底导热的数 学描写,并计算锅底两表面的温度。 解: 28一种用比较法测定导热系数装置的原理示于附图中。将导热系数已知的标准材料与被测材料做成 相同直径的圆柱,且标准材料的两段圆柱分别压紧置于被测材料的两端。在三段试样上分别布置三 对测定相等间距两点间温差的热电偶。试样的四周绝热良好(图中未示出) 。已知试样两端的温度分 别为th=400℃、tc=300℃、△t=2.49℃,△t1=3.56℃、△t.2=3.60℃,试确定被测材料的导热系数, 并讨论哪些因素会影响△t1与△ti,2不相等? 解: 【第10页共284页】
【第 10 页 共 284 页】 解: 由题意得 3 3 2 2 1 1 1 2 1 2 1 1 h h t t A = 37.2 0.1 0.0095 0.07 0.152 45 0.000794 2.5 1 1.5 1 30 ( 2) =357.14W 357.14×3600=1285.6KJ 2-3 有一厚为 20mm 的平板墙,导热系数为 1.3W /(m.K ) 。为使每平方米墙的热损失不超过 1500W, 在外表面上覆盖了一层导热系数为 0.12W /(m.K ) 的保温材料。 已知复合壁两侧的温度分别为 750℃ 及 55℃,试确定此时保温层的厚度。 解: 依据题意,有 1500 1.3 0.12 0.020 750 55 2 2 2 1 1 1 2 t t q ,解得: 2 0.05375m 2-4 一 烘 箱 的 炉 门 由 两 种 保 温 材 料 A 及 B 组 成 , 且 A 2 B ( 见 附 图 ) 。 已 知 A 0.1W /(m.K) , B 0.06W /(m.K) ,烘箱内空气温度 t f 1 400 ℃,内壁面的总表面传热系数 50 /( . ) h1 W m K 。为安全起见, 希望烘箱炉门的 外表面温度不得高于 50℃。设可把炉门导热作为 一 维 问 题 处 理 , 试 决 定 所 需 保 温 材 料 的 厚 度 。 环 境 温 度 f 2 t 25 ℃ , 外 表 面 总 传 热 系 数 9.5 /( . ) 2 h2 W m K 。 解: 热损失为 1 1 2 2 1 f f B B A A f fw h t t h t t t t q 又 t fw 50 ℃; A B 联立得 A 0.078m; B 0.039m 2-5 对于无限大平板内的一维导热问题,试说明在三类边界条件中,两侧边界条件的哪些组合可以 使平板中的温度场获得确定的解? 解:两侧面的第一类边界条件;一侧面的第一类边界条件和第二类边界条件;一侧面的第一类边界 条件和另一侧面的第三类边界条件;一侧面的第一类边界条件和另一侧面的第三类边界条件。 平壁导热 2-6 一火箭发动机燃烧室是直径为 130mm 的圆筒体,厚 2.1mm,导热系数为 23.2W/(m ·K) 。圆筒壁 外用液体冷却,外壁温度为 240℃。测得圆筒体的热流密度为 4.8×106 W/㎡,其材料的最高允许温 度为 700℃。试判断该燃烧室壁面是否工作于安全温度范围内? 解: 2-7 如附图所示的不锈钢平底锅置于电器灶具上被加热,灶具的功率为 1000W,其中 85%用于加热 平底锅。锅底厚 δ=3 ㎜,平底部分直径 d=200 ㎜,不锈刚的导热系数 λ=18W/ (m· K),锅内汤料 与锅底的对流传热表面传热系数为 2500W/(㎡· K),流体平均温度 tf=95℃。试列出锅底导热的数 学描写,并计算锅底两表面的温度。 解: 2-8 一种用比较法测定导热系数装置的原理示于附图中。 将导热系数已知的标准材料与被测材料做成 相同直径的圆柱,且标准材料的两段圆柱分别压紧置于被测材料的两端。在三段试样上分别布置三 对测定相等间距两点间温差的热电偶。试样的四周绝热良好(图中未示出) 。已知试样两端的温度分 别为 th=400℃、 tc=300℃、 Δtr=2.49℃, Δ tt,1=3.56℃、 Δtt,2=3.60℃,试确定被测材料的导热系数, 并讨论哪些因素会影响 Δtt,1 与Δtt,2 不相等? 解: