
信湯怀蔬学悦化学化工学院 College of Chemistry and Chemical Engineering,Xinyang Normal University 第3章分析化学中的误差及数据处理 3.1分析化学中的误差 3.2有效数字及其运算规则 3.3分析化学中的数据处理 3.4显著性检验 3.5可疑值取舍 3.6回归分析法 3.7提高分析结果准确度的方法
第3章 分析化学中的误差及数据处理 3.1 分析化学中的误差 3.2 有效数字及其运算规则 3.3 分析化学中的数据处理 3.4 显著性检验 3.5 可疑值取舍 3.6 回归分析法 3.7 提高分析结果准确度的方法

3.1分析化学中的误差 必然存在 减小合理 分析的核心是准确的“量”的概念,凡是测 量就有误差,减少测量误差是分析工作的重点之 2
2 3.1 分析化学中的误差 分析的核心是准确的“量”的概念, 凡是测 量就有误差, 减少测量误差是分析工作的重点之 一. 必然存在 减小 合理

3.1.1误差和偏差 l.真值T(True value) 某一物理量本身具有的、客观存在的真实值。 真值是未知的、客观存在的量。在特定情况下认为是已知 的: 理论真值(如化合物的理论组成) 计量学约定真值(如国际计量大会确定的长度、质量、物质 的量单位等等) 相对真值(高一级精度的测量值相对于低一级精度的测量值, 如人们采用可靠办法、使用最精密仪器,经不同实验室、不 同人员进行平行分析,用数理统计方法得到的各组分相对准 确的含量) 3
3 1. 真值 T (True value) 某一物理量本身具有的、客观存在的真实值。 真值是未知的、客观存在的量。在特定情况下认为是已知 的: 3.1.1 误差和偏差 理论真值(如化合物的理论组成) 计量学约定真值(如国际计量大会确定的长度、质量、物质 的量单位等等) 相对真值(高一级精度的测量值相对于低一级精度的测量值, 如人们采用可靠办法、使用最精密仪器,经不同实验室、不 同人员进行平行分析,用数理统计方法得到的各组分相对准 确的含量)

2.误差(Error): 「E>0 绝对误差E=X-XT E<0 绝对误差单位与测量值单位相同,误差越小,准确度越 高。 相对误差 E Ex100%= x-x江×100% XT 绝对误差有大小、正负之分,反映的是误差在真实值中 所占的比例大小。绝对误差相同的条件下,待测组分含 量越高,相对误差越小,反之则越大
4 2.误差(Error): 绝对误差 E = x - xT E>0 E<0 100% 100% T r T T E x x E x x − 相对误差 = = 绝对误差单位与测量值单位相同,误差越小,准确度越 高。 绝对误差有大小、正负之分,反映的是误差在真实值中 所占的比例大小。绝对误差相同的条件下,待测组分含 量越高,相对误差越小,反之则越大

如:对于1000kg和10kg,绝对误差相同(±1kg),但产生的相 对误差却不同。 ±1 E,= ×100%=±0.1% 1000 E,=x100%=±10% ±1 10 ·绝对误差和相对误差都有正负之分。 5
5 如:对于1000kg和10kg ,绝对误差相同(±1kg),但产生的相 对误差却不同。 • 绝对误差和相对误差都有正负之分。 r 1 E 100% 0.1% 1000 = = r 1 E 100% 10% 10 = =

例:用重量分析法测定纯BaCl2·2H2O试剂中Ba的含量, 结果为56.14%,56.16%,56.17%,56.13%,计算测定结 果的绝对误差和相对误差。 先求4次测定的平均值 =(56.14%+56.16%+56.17%+56.13%)/4=56.15% 纯BaCl2·2H20中Ba的理论含量为真值,查A,(Ba)=137.33, M(BaC2·2H20)=244.27,则 x=(137.33/244.27)×100%=56.22% 绝对误差E=下-xT=56.15%-56.22%=-0.07% 相对误差E,=E/xT×100%=-0.07%156.22%×100%=-0.12% 6
6 例:用重量分析法测定纯BaCl2﹒2H2O试剂中Ba的含量, 结果为56.14%,56.16%,56.17%,56.13%,计算测定结 果的绝对误差和相对误差。 先求4次测定的平均值 =( 56.14%+56.16%+56.17%+56.13% )/4 =56.15% 纯BaCl2﹒2H2O中Ba的理论含量为真值,查Ar(Ba)=137.33, Mr( BaCl2﹒2H2O )=244.27,则 xT =(137.33/244.27)×100%=56.22% 绝对误差 E= - xT= 56.15%- 56.22%= -0.07% 相对误差 Er=E/xT ×100%=-0.07%/56.22% ×100%=-0.12% x x

3.偏差测量结果的离散性 1)偏差(devoation) 测量值与平均值的差值,用d表示 d=x-x ∑l=0 水均位 n 7
7 3. 偏差 测量结果的离散性 测量值与平均值的差值,用 d表示 1 2 1 1 n n i i x x x x x n n = + + + 算术平均值 = = d = x - x ∑di = 0 1) 偏差(devoation)

2)平均偏差(mean deviation) d=(d+ldl++ld,D=∑ld ·通常以单次测量偏差的绝对值的算术平均值即平均 偏差d来表示精密度。 3)相对平均偏差(relative mena deviation) d 相对平均偏差d,=×100%= ×100% nx 注意:不计正负号,d则有正负之分。 8
8 2)平均偏差(mean deviation) • 通常以单次测量偏差的绝对值的算术平均值即平均 偏差 来表示精密度。 3) 相对平均偏差(relative mena deviation) 注意: 不计正负号,di则有正负之分。 d 1 2 1 1 1 ( ) n n i i d d d d d n n = = + + + = 1 100% 100% n i i r x x d d x nx = − = = 相对平均偏差

·例:测定某试样中氯的百分含量,三次分析结果分别为 25.12、25.21和25.09,计算平均偏差和相对平均偏差。如 果真实百分含量为25.10,计算绝对误差和相对误差。 。解:平均值 X-2512+2521+2509-2514K% 3 ·平均偏差 a=002+007+005 005% 3 ·相对平均偏差=(0.05/25.14)X1000%=2%0 ·绝对误差E=25.14-25.10=+0.04(%) ·相对误差=什0.04/25.10)×1000%0=+2%0 9
9 • 例:测定某试样中氯的百分含量,三次分析结果分别为 25.12、25.21和25.09,计算平均偏差和相对平均偏差。如 果真实百分含量为25.10,计算绝对误差和相对误差。 • 解:平均值 • 平均偏差 • 相对平均偏差=(0.05/25.14)×1000‰=2‰ • 绝对误差E=25.14-25.10=+0.04(%) • 相对误差=(+0.04/25.10)×1000‰=+2‰ X = + + = 2512 2521 2509 3 2514 . . . . (%) d = + + = 0 02 0 07 0 05 3 0 05 . . . . (%)
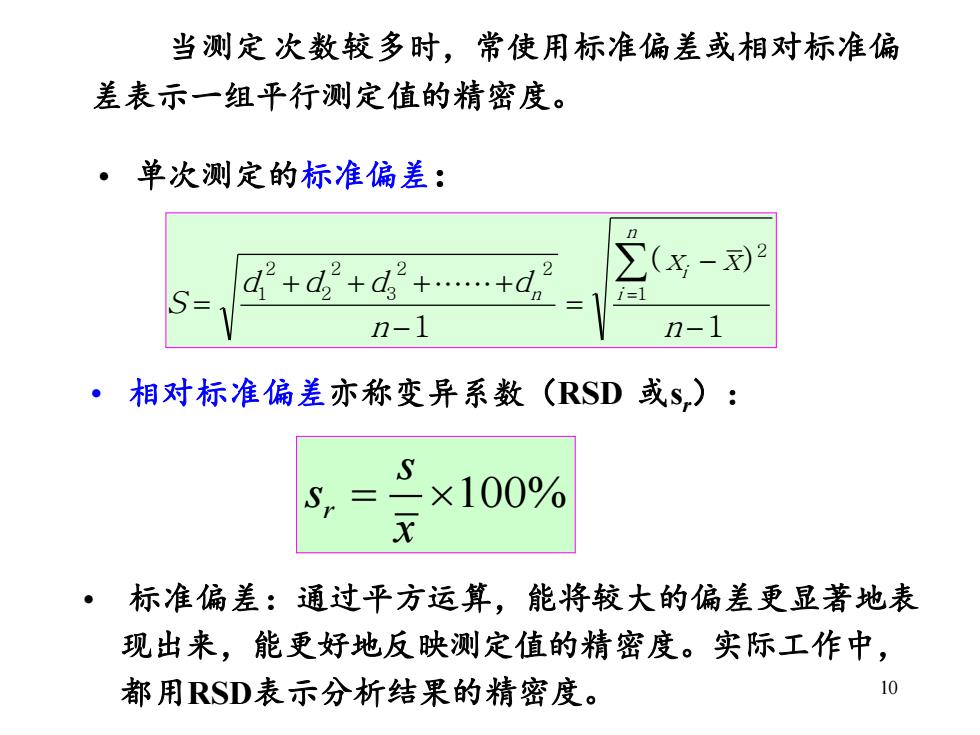
当测定次数较多时,常使用标准偏差或相对标准偏 差表示一组平行测定值的精密度。 ·单次测定的标准偏差: n (x-利 S= d+d+d2+.+d2 i=1 n-1 n-1 ·相对标准偏差亦称变异系数(RSD或S): S ×100% X ·标准偏差:通过平方运算,能将较大的偏差更显著地表 现出来,能更好地反映测定值的精密度。实际工作中, 都用RSD表示分析结果的精密度。 10
10 当测定 次数较多时,常使用标准偏差或相对标准偏 差表示一组平行测定值的精密度。 • 单次测定的标准偏差: • 相对标准偏差亦称变异系数(RSD 或sr): r 100% s s x = • 标准偏差:通过平方运算,能将较大的偏差更显著地表 现出来,能更好地反映测定值的精密度。实际工作中, 都用RSD表示分析结果的精密度。 S d d d d n x x n n i i n = + + + + − = − − = 1 2 2 2 3 2 2 2 1 1 1 ( )