
Chapter 8 Atomic Structure 8.1 The atomic structure of hydrogen x 8.2 The atomic structure of many-electron atoms x 8.3 Periodic law of elements
8.1 The atomic structure of hydrogen 8.2 The atomic structure of many-electron atoms 8.3 Periodic law of elements Chapter 8 Atomic Structure

8.1 The atomic structure of hydrogen 8.1.1 The hydrogen spectrum and Bohr's theory 8.1.2 The dual nature of the electron 8.1.3 Schrodinger equation and quantum numbers 8.1.4 The ground state of H atoms 8.1.5 The excited state of HAtoms 回
8.1.1 The hydrogen spectrum and Bohr’s theory 8.1 The atomic structure of hydrogen 8.1.5 The excited state of H Atoms 8.1.4 The ground state of H atoms 8.1.3 Schrödinger equation and quantum numbers 8.1.2 The dual nature of the electron
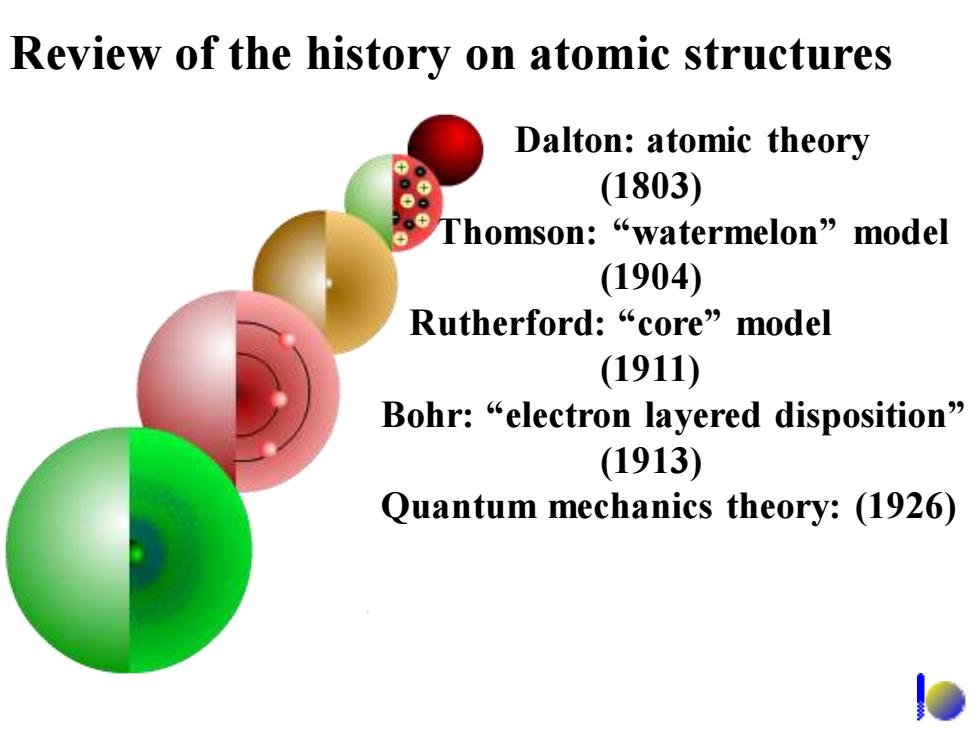
Review of the history on atomic structures Dalton:atomic theory (1803) Thomson:“watermelon”nodel (1904) Rutherford:“core”model (1911) Bohr:“electron layered disposition'” (1913) Quantum mechanics theory:(1926)
Review of the history on atomic structures Dalton: atomic theory (1803) Thomson: “watermelon” model (1904) Rutherford: “core” model (1911) Bohr: “electron layered disposition” (1913) Quantum mechanics theory: (1926)

8.1.1 The hydrogen spectrum and Bohr's theory 1.Light:a component of electromagnetic radiation 103m 1m 10-3m 10-6m 10-9m 10-12m 10-15m Long waves Radio waves Infrared Ultraviolet X-rays Gamma rays red orange green grass blue purple v⅓ 5×1014 6×1014 7×1014
1. Light: a component of electromagnetic radiation 8.1.1 The hydrogen spectrum and Bohr’s theory red orange green grass blue purple
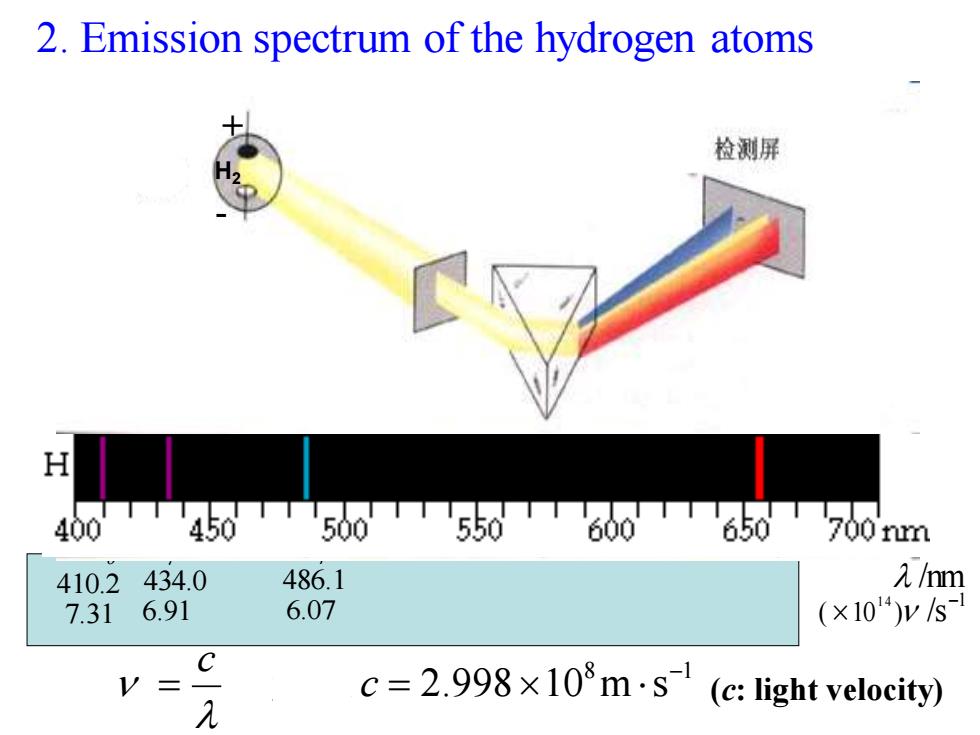
2.Emission spectrum of the hydrogen atoms 检测屏 H 400TTT450T500550T600T650700nm 410.2434.0 486.1 1/m 7.31 6.91 6.07 (×104)ys- C V= 元 c=2.998×103m·s(c:light velocity))
2. Emission spectrum of the hydrogen atoms 8 1 2.998 10 m s − = c = c 光速 Hα 656.3 4.57 Hβ 486.1 6.07 Hγ 434.0 6.91 Hδ 410.2 7.31 /nm1 ( 10 ) /s 1 4 − H2 + - (c: light velocity)

The features of hydrogen spectrum: discontinuous spectrum (line spectrum) the frequency of the visible line spectrum meets with the following empirical equation: v=3289x10(s n=3 red红(Ha) n=4 blueness青(HB) n=3,4,5,6,. n=5 blue-purple蓝紫HY)) n=6 purple紫(H6) But what does 2,n,3.289X1015mean in the empirical equation?Unclear at that time
• discontinuous spectrum (line spectrum) • the frequency of the visible line spectrum meets with the following empirical equation: 1 2 2 1 5 )s 1 2 1 3.289 10 ( − = − n v n= 3,4,5,6, … But what does 2,n,3.289×1015 mean in the empirical equation? Unclear at that time The features of hydrogen spectrum: n = 3 red 红(Hα) n = 4 blueness 青(Hβ) n = 5 blue-purple 蓝紫(Hγ) n = 6 purple 紫(Hδ)

3.Bohr's theory Three major assumptions of Bohr's theory DAn electron in an atom could be located only in certain orbits that have particular radii and energies; 2Usually,an electron would remain in the orbit which is the most close to the nucleus.The atom is said to be in its ground state under this condition,which corresponds to the most stable energy state;Energy absorbed by the atom causes the electron to move from the orbits close to the nucleus to those far from it,then the atom is said to be in an excited state
3.Bohr’s theory Three major assumptions of Bohr’s theory : ①An electron in an atom could be located only in certain orbits that have particular radii and energies; ②Usually, an electron would remain in the orbit which is the most close to the nucleus. The atom is said to be in its ground state under this condition, which corresponds to the most stable energy state; Energy absorbed by the atom causes the electron to move from the orbits close to the nucleus to those far from it, then the atom is said to be in an excited state

3An electron originally in a higher energy orbit will fall back to a lower energy orbit.As a result,a photon with energy hv is given off. hclh=hv=E2-E E:the energy of an orbit E2-E1 h:Planck's constant h The H spectra can be well explained with Bohr's theory
③An electron originally in a higher energy orbit will fall back to a lower energy orbit. As a result, a photon with energy h is given off. h E E h E E 2 1 2 1 − = = − E:the energy of an orbit h:Planck’s constant The H spectra can be well explained with Bohr’s theory hc/ =
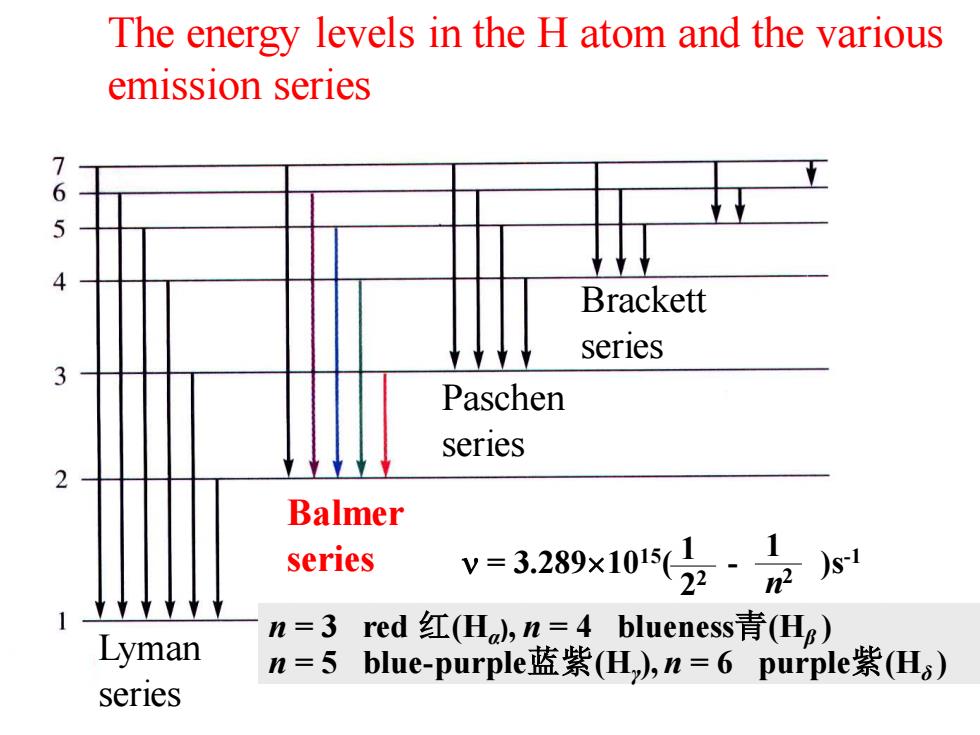
The energy levels in the H atom and the various emission series 7 6 Brackett series Paschen series Balmer series v=3280x105·0 Lyman n=3red红(Ha,n=4 blueness青(Hg) n=5blue-purplej蓝紫(H),n=6 purple紫(H) series
The energy levels in the H atom and the various emission series Balmer series Lyman series Paschen series Brackett series n = 3 red 红(Hα ), n = 4 blueness青(Hβ ) n = 5 blue-purple蓝紫(Hγ ), n = 6 purple紫(Hδ ) = 3.2891015( - )s 1 -1 2 2 1 n 2

y=3.289×1015(1 n n2>n1 △E=hv =6.626×1034J-s×3.289×1015( 之 =2.179×1018(1 2 RH:Rydberg constant, 2.179×1018J
-1 2 2 2 1 15 )s 1 1 3.289 10 ( n n v = − n2 n1 E = hv RH:Rydberg constant, 2.179×10-18J. ) 1 1 ( 2 2 2 1 H n n E = R − )J 1 1 2.179 10 ( 2 2 2 1 -1 8 n n = − -1 2 2 2 1 3 4 1 5 )s 1 1 6.626 10 J s 3.289 10 ( n n = − −