
耕作学实验指导书 河北农业大学农学院 作物栽培与耕作系 2005年8月修订
耕作学实验指导书 河北农业大学农学院 作物栽培与耕作系 2005 年 8 月修订

目录 实验一作物种类与复种形式的确定.1 实验二作物布局优化方法之一原理与基本方法. .5 实验三作物布局优化方法之二一最优化计算机软件的应用.10 实验四轮作制度设计.12 实验五土地耕作制设计.15 实验六土壤施肥制的设计.17 附录1选修实验目录.32
1 目 录 实验一 作物种类与复种形式的确定.1 实验二 作物布局优化方法之—— 原理与基本方法.5 实验三 作物布局优化方法之二 — 最优化计算机软件的应用.10 实验四 轮作制度设计.12 实验五 土地耕作制设计.15 实验六 土壤施肥制的设计.17 附录 1 选修实验目录.32

实验一种植制度的农业资源分析 一一作物类型与复种形式的确定 一、目的意义: 农业的稳产高产是以作物与其环境的高度统一与适应为基础的。依据当地的 气候、土壤及生产经济条件确定所种植的作物种类及复种方式,是安排农业生产 的首要问题。在我们还不能大面积控制作物环境的条件下,因地制宜,适地适作 是农业费省效宏的有效手段。本实验旨在掌握各作物生态适应性及所规划地区生 态条件的基础上,运用所掌握的生态学与耕作学知识,学会分析种植制度与资源 关系的方法,为耕作制度设计奠定基础。 二、原则: 1.以作物与其环境的统一为总原则。不同地区在地理、地形、地貌、气候, 土壤及生产条件诸方面存在差异,而各种作物又要求不同的生活环境,只有使作 物与环境相互统一,组成一个协调的生态系统,作物才能稳产高产。 2.从大农业观出发,农林草综合发展,在充分利用农业资源,大力发展商品 生产的同时,要积极保护农业资源,保证农业生态系统的良好循环,以同时获得 高的经济效益和生态效益。 3.既要考虑因地制宜,适地适作,又要注意满足人民群众及社会的多种需要, 在发展粮食生产的同时,发展经济作物、果品蔬菜及饲料绿肥作物的生产。 三、依据: 1.作物对热量的要求: 热量是决定作物种类与复种方式的首要条件。多种作物在其系统发育中形成 了对热量要求的不同类型。因此,可将作物分为耐寒作物、低温作物、中温作物 及喜温作物,它们对温度的要求如附表1。 某作物在此地能否种植,首先取决于当地生长季内的积温状况。当一个生长 季内的积温除能满足一茬作物需要(考虑一定的保证率,一般80%以上)尚有剩余 时,就可考虑复种。复种形式可根据热量及其它条件采取一年两熟、二年三熟等 熟制类型。根据条件可采取套作复种或平作复种。以冬小麦为前茬的平作复种作 需≥0℃积温,如附表2。 2.作物对水分的要求
2 实验一 种植制度的农业资源分析 ——作物类型与复种形式的确定 一、目的意义: 农业的稳产高产是以作物与其环境的高度统一与适应为基础的。依据当地的 气候、土壤及生产经济条件确定所种植的作物种类及复种方式,是安排农业生产 的首要问题。在我们还不能大面积控制作物环境的条件下,因地制宜,适地适作 是农业费省效宏的有效手段。本实验旨在掌握各作物生态适应性及所规划地区生 态条件的基础上,运用所掌握的生态学与耕作学知识,学会分析种植制度与资源 关系的方法,为耕作制度设计奠定基础。 二、原则: 1.以作物与其环境的统一为总原则。不同地区在地理、地形、地貌、气候, 土壤及生产条件诸方面存在差异,而各种作物又要求不同的生活环境,只有使作 物与环境相互统一,组成—个协调的生态系统,作物才能稳产高产。 2.从大农业观出发,农林草综合发展,在充分利用农业资源,大力发展商品 生产的同时,要积极保护农业资源,保证农业生态系统的良好循环,以同时获得 高的经济效益和生态效益。 3.既要考虑因地制宜,适地适作,又要注意满足人民群众及社会的多种需要, 在发展粮食生产的同时,发展经济作物、果品蔬菜及饲料绿肥作物的生产。 三、依据: 1.作物对热量的要求: 热量是决定作物种类与复种方式的首要条件。多种作物在其系统发育中形成 了对热量要求的不同类型。因此,可将作物分为耐寒作物、低温作物、中温作物 及喜温作物,它们对温度的要求如附表 1。 某作物在此地能否种植,首先取决于当地生长季内的积温状况。当一个生长 季内的积温除能满足—茬作物需要(考虑一定的保证率,—般 80%以上)尚有剩余 时,就可考虑复种。复种形式可根据热量及其它条件采取一年两熟、二年三熟等 熟制类型。根据条件可采取套作复种或平作复种。以冬小麦为前茬的平作复种作 需≥0℃积温,如附表 2。 2.作物对水分的要求:

水分是影响作物配置的主要因素,根据作物的生物学特性及需水系数可将其 分为喜水作物与耐旱作物两大类。各类作物的蒸腾系数及需水特性如附表3。 但应注意,同一作物的产量水平不同,需水系数有变化。另外,一个作物对 干旱及涝渍的忍耐程度也反映了它的需水特性。 根据作物的需水特性,查明当地的自然降水,水分分布及地上地下供水对作 物各生育期需水满足程度(变率和保证率),以此来确定当地的主导作物和次级作 3.作物对土壤的要求: 土壤是作物生长的基质,是水肥气热的提供者,它综合反映着气候和地力条 件。如果说热量和水分决定着作物种植地带和区域,那么在同一地带或地区内的 不同生态区,究竟种哪些作物及各作物间的比例如何,则在很大程度上取决于士 壤,特别是土壤的质地、沙粘、酸碱度、盐分及地力等。不同作物对土壤有不同 的要求,如甘薯、豆类、花生等适宜种于地势高燥、通透性较好的沙质土壤上: 而小麦、玉米、高梁则宜种于肥力较高的壤质、粘壤质土壤上,有的作物对瘠薄、 盐碱等特种土壤有较好的适应性,各种作物对土壤的要求如附表4。另外,地形和 农田微地貌也影响作物布局,应一并考虑。 四、方法步骤: 1.调查了解本地区的自然条件、生产及社会经济条件。 ()气侯条件:包括一年内的温度变化及年均温,各农业界限的积温量。年极 端温度及日期,年初终霜及年无霜期,年降水分布及降水量,空气温度及蒸降比, 日照风力资料,冷冻、旱涝及干热风、冰雹等灾害性天气的发生规律。 (②)土壤条件:包括地形、地貌、土壤种类及土壤肥力,各种作物的生产性能 等,绘制12000~4000的土壤类型分布图。 (3)水文资料:地上、地下水源,水质,水位,年地下水开采量及最大可开采 量。 (④)生产条件:这里主要是考虑农业生产条件对土壤肥力及环境的改善对作物 的影响,包括每亩耕地可灌水、施肥数量及农业机械的作用程度。 (⑤)作物条件:当地作物布局的演变历史,历年各作物产量,各作物对当地灾 害性气候的反应。通过分析可初步评价原有作物在当地的生态适应性,为以后工 作奠定基础。 3
3 水分是影响作物配置的主要因素,根据作物的生物学特性及需水系数可将其 分为喜水作物与耐旱作物两大类。各类作物的蒸腾系数及需水特性如附表 3。 但应注意,同一作物的产量水平不同,需水系数有变化。另外,一个作物对 干旱及涝渍的忍耐程度也反映了它的需水特性。 根据作物的需水特性,查明当地的自然降水,水分分布及地上地下供水对作 物各生育期需水满足程度(变率和保证率),以此来确定当地的主导作物和次级作 物。 3.作物对土壤的要求: 土壤是作物生长的基质,是水肥气热的提供者,它综合反映着气候和地力条 件。如果说热量和水分决定着作物种植地带和区域,那么在同一地带或地区内的 不同生态区,究竟种哪些作物及各作物间的比例如何,则在很大程度上取决于土 壤,特别是土壤的质地、沙粘、酸碱度、盐分及地力等.不同作物对土壤有不同 的要求,如甘薯、豆类、花生等适宜种于地势高燥、通透性较好的沙质土壤上; 而小麦、玉米、高梁则宜种于肥力较高的壤质、粘壤质土壤上,有的作物对瘠薄、 盐碱等特种土壤有较好的适应性,各种作物对土壤的要求如附表 4。另外,地形和 农田微地貌也影响作物布局,应一并考虑。 四、方法步骤: 1. 调查了解本地区的自然条件、生产及社会经济条件。 (1) 气侯条件:包括一年内的温度变化及年均温,各农业界限的积温量。年极 端温度及日期,年初终霜及年无霜期,年降水分布及降水量,空气温度及蒸降比, 日照风力资料,冷冻、旱涝及干热风、冰雹等灾害性天气的发生规律。 (2) 土壤条件:包括地形、地貌、土壤种类及土壤肥力,各种作物的生产性能 等,绘制 1:2000~4000 的土壤类型分布图。 (3) 水文资料:地上、地下水源,水质,水位,年地下水开采量及最大可开采 量。 (4) 生产条件:这里主要是考虑农业生产条件对土壤肥力及环境的改善对作物 的影响,包括每亩耕地可灌水、施肥数量及农业机械的作用程度。 (5) 作物条件:当地作物布局的演变历史,历年各作物产量,各作物对当地灾 害性气候的反应。通过分析可初步评价原有作物在当地的生态适应性,为以后工 作奠定基础

(6)根据市场和自身需求制订计划(目标)产量。 2.根据确定作物类型与复种方式的原则,依据当地的热量、水分、土壤及生 产等条件拟定当地的种植制度,并给以相应的评述。 五、实验材料: 1.南皮县各月逐旬温度、降水、日照材料。附表5、6。 2.南皮县徐朗中村土壤类型分布图。图1。 3.生产条件:春季可供水72000方。 六、作业:试拟订本村作物组成及复种类型、方式,并给予相应的评述
4 (6) 根据市场和自身需求制订计划(目标)产量。 2. 根据确定作物类型与复种方式的原则,依据当地的热量、水分、土壤及生 产等条件拟定当地的种植制度,并给以相应的评述。 五、实验材料: 1.南皮县各月逐旬温度、降水、日照材料。附表 5、6。 2.南皮县徐朗中村土壤类型分布图。图 1。 3.生产条件:春季可供水 72000 方。 六、作业:试拟订本村作物组成及复种类型、方式,并给予相应的评述

实验二作物布局的调整与设计 一、目的意义: 作物布局是指在一个地区或一个生产单位所种植的作物种类及各作物面积比 例的安排。作物布局是组织农业生产的一项重要战略措施,它关系到能否因地制 宜:充分而合理地利用当地农业资源:达到农业生产的高产、稳产、增益的问题。 一个地区采用不同的作物布局方案,会收到不同的经济及生态效果。作物布 局方案的拟定属于多变量、多目标的复杂问题,它不仅要考虑当地的自然条件, 而且受到当地的社会经济条件技术水平及国家、集体、个人对于农业生产要求的 制约,依靠一般的定性分析方法很难对这种具有多个因素、多项目标的复杂问题 进行综合的考虑与平衡,找出最优的方案。最优化技术中的线性规划能够帮助我 们对此类复杂问题做出定量分析,并得出最优方案。因此,作物布局的线性规划 就是利用线性规划的理论与技术来解决在一定的自然条件和社会经济资源条件下 能够达到最佳技术、经济及生态效果的作物最佳配置比例的最优化技术方法。 通过本实验,了解从线性规划方法来制定作物布局方案的原理和方法,培养 系统分析,综合平衡的能力。 二、线性规划方法的作用和意义: 线性规划是系统工程中最优化技术方法之一。它主要解决二方面的问题。其 一是“省”一一如何用最少的人力、物力、财力等资源来完成既定的(定量的)任务: 其二是“多”一一如何合理地充分地利用现有的资源(人力、物力、财力等资源) 来完成最大量的任务。 线性规划设计是在完成了对大量定性资料及对系统的定性的描述性的分析基 础上,为了进一步明确各变量之间的关系,协调与寻求各部门生产的最优比例与 组合而进行的定量分析。它是在电子计算机的帮助下,依靠建立数学模型的方法, 经过多次的反馈、修正完成的。 三、线性规划设计的一般步骤: 1.资料的收集:在确定了所需要研究系统的范围之后,需要进行对系统的考 察和资料的收集,包括系统的性质、特点,系统的组成分,组成分间的制约、协 同、转化关系及其定性的资料,系统与环境之间的关系等。 2.制定规划目标:规划目标即人们对所研究的系统所追求的目标。一般选择 5
5 实验二 作物布局的调整与设计 —、目的意义: 作物布局是指在—个地区或一个生产单位所种植的作物种类及各作物面积比 例的安排。作物布局是组织农业生产的一项重要战略措施,它关系到能否因地制 宜;充分而合理地利用当地农业资源;达到农业生产的高产、稳产、增益的问题。 一个地区采用不同的作物布局方案,会收到不同的经济及生态效果。作物布 局方案的拟定属于多变量、多目标的复杂问题,它不仅要考虑当地的自然条件, 而且受到当地的社会经济条件技术水平及国家、集体、个人对于农业生产要求的 制约,依靠一般的定性分析方法很难对这种具有多个因素、多项目标的复杂问题 进行综合的考虑与平衡,找出最优的方案。最优化技术中的线性规划能够帮助我 们对此类复杂问题做出定量分析,并得出最优方案。因此,作物布局的线性规划 就是利用线性规划的理论与技术来解决在一定的自然条件和社会经济资源条件下 能够达到最佳技术、经济及生态效果的作物最佳配置比例的最优化技术方法。 通过本实验,了解从线性规划方法来制定作物布局方案的原理和方法,培养 系统分析,综合平衡的能力。 二、线性规划方法的作用和意义: 线性规划是系统工程中最优化技术方法之一。它主要解决二方面的问题。其 一是“省”——如何用最少的人力、物力、财力等资源来完成既定的(定量的)任务; 其二是“多”——如何合理地充分地利用现有的资源(人力、物力、财力等资源) 来完成最大量的任务。 线性规划设计是在完成了对大量定性资料及对系统的定性的描述性的分析基 础上,为了进一步明确各变量之间的关系,协调与寻求各部门生产的最优比例与 组合而进行的定量分析。它是在电子计算机的帮助下,依靠建立数学模型的方法, 经过多次的反馈、修正完成的。 三、 线性规划设计的一般步骤: 1.资料的收集:在确定了所需要研究系统的范围之后,需要进行对系统的考 察和资料的收集,包括系统的性质、特点,系统的组成分,组成分间的制约、协 同、转化关系及其定性的资料,系统与环境之间的关系等。 2.制定规划目标:规划目标即人们对所研究的系统所追求的目标。一般选择

能够表示此系统的特性,人们所追求的诸如产品总产量总产值、净收益、低成本 等作为目标:规划的结果是求出其极值。规划目标是线性规划设计的核心,约束 条件的建立要求以目标来确定。 3.建立约束条件:为了实现所追求的目标安排生产时,受到的各种限制及人 为的客观要求等均可作为约束条件,这往往要依靠规划前的一系列定性分析及以 往的经验来确定,如自然资料限制,社会资源、财力资源限制以及人为要求限制(必 须量限制)等。 4.建立模型:就是将原来的生产问题抽象为数学问题。首先根据问题的性质 确定目标函数,然后根据问题的内部关系建立约束方程即一组线性等式或不等 式)。这里关键的是变量参数的确定,它直接关系着规划的效果与成败,这往往需 要规划前的大量调查、测算与实验,并进行一些必要的定性、定量分析。 5.问题的求解:求解线性规划问题的方法很多,应用最普遍的方法是单纯形 法,原则上,此法可以求解一些线性规划问题。当所研究的问题很复杂时,并可 借助电子计算机求解。 6.结果的灵敏度分析:所谓灵敏度就是目标函数的最优值对于约束条件的单 位变化的反应灵敏度。对于每个约束条件进行灵敏度分析,有助于我们认识那些 灵敏度高的约束,可提醒我们在对此约束所做的调查,试验以及数据的处理都应 具有较高的精度。通过灵敏度分析,还可进一步判断在规划中影响限制最优目标 的主要因素。 四、线性规划问题的举例与求解: (一)举例:一块农田的95亩小麦收获后,准备种植三种秋作,玉米、谷子 和甘薯。历年三种作物的平均产量为600公斤、400公斤、300公斤,并已知玉米 每生产600公斤需要有机肥8车,化肥50公斤,投工12个,生产400公斤谷子 需有机肥5车,化肥20公斤,投工10个,生产300公斤甘薯需有机肥2车.投 工16个.但因条件限制,供给此块农田的有机肥只有400车,化肥2000公斤, 投工1200个。问如何制定种植计划才能使总产量最高。 这实际上是一个求在一定资源条件下,如何合理安排各作物生产的比例,以 获得最高生产效益的问题。 为了便于分析,列出此问题的数据表: 6
6 能够表示此系统的特性,人们所追求的诸如产品总产量总产值、净收益、低成本 等作为目标;规划的结果是求出其极值。规划目标是线性规划设计的核心,约束 条件的建立要求以目标来确定。 3.建立约束条件:为了实现所追求的目标安排生产时,受到的各种限制及人 为的客观要求等均可作为约束条件,这往往要依靠规划前的一系列定性分析及以 往的经验来确定,如自然资料限制,社会资源、财力资源限制以及人为要求限制(必 须量限制)等。 4.建立模型:就是将原来的生产问题抽象为数学问题。首先根据问题的性质 确定目标函数,然后根据问题的内部关系建立约束方程(即一组线性等式或不等 式)。这里关键的是变量参数的确定,它直接关系着规划的效果与成败,这往往需 要规划前的大量调查、测算与实验,并进行一些必要的定性、定量分析。 5.问题的求解:求解线性规划问题的方法很多,应用最普遍的方法是单纯形 法,原则上,此法可以求解一些线性规划问题。当所研究的问题很复杂时,并可 借助电子计算机求解。 6.结果的灵敏度分析:所谓灵敏度就是目标函数的最优值对于约束条件的单 位变化的反应灵敏度。对于每个约束条件进行灵敏度分析,有助于我们认识那些 灵敏度高的约束,可提醒我们在对此约束所做的调查,试验以及数据的处理都应 具有较高的精度。通过灵敏度分析,还可进一步判断在规划中影响限制最优目标 的主要因素。 四、线性规划问题的举例与求解: (一)举例:一块农田的 9 5 亩小麦收获后,准备种植三种秋作,玉米、谷子 和甘薯。历年三种作物的平均产量为 6 00 公斤、400 公斤、300 公斤,并已知玉米 每生产 600 公斤需要有机肥 8 车,化肥 50 公斤,投工 12 个,生产 400 公斤谷子 需有机肥 5 车,化肥 2 0 公斤,投工 1 0 个,生产 300 公斤甘薯需有机肥 2 车.投 工 1 6 个.但因条件限制,供给此块农田的有机肥只有 400 车,化肥 2000 公斤, 投工 1200 个。问如何制定种植计划才能使总产量最高。 这实际上是一个求在一定资源条件下,如何合理安排各作物生产的比例,以 获得最高生产效益的问题。 为了便于分析,列出此问题的数据表:
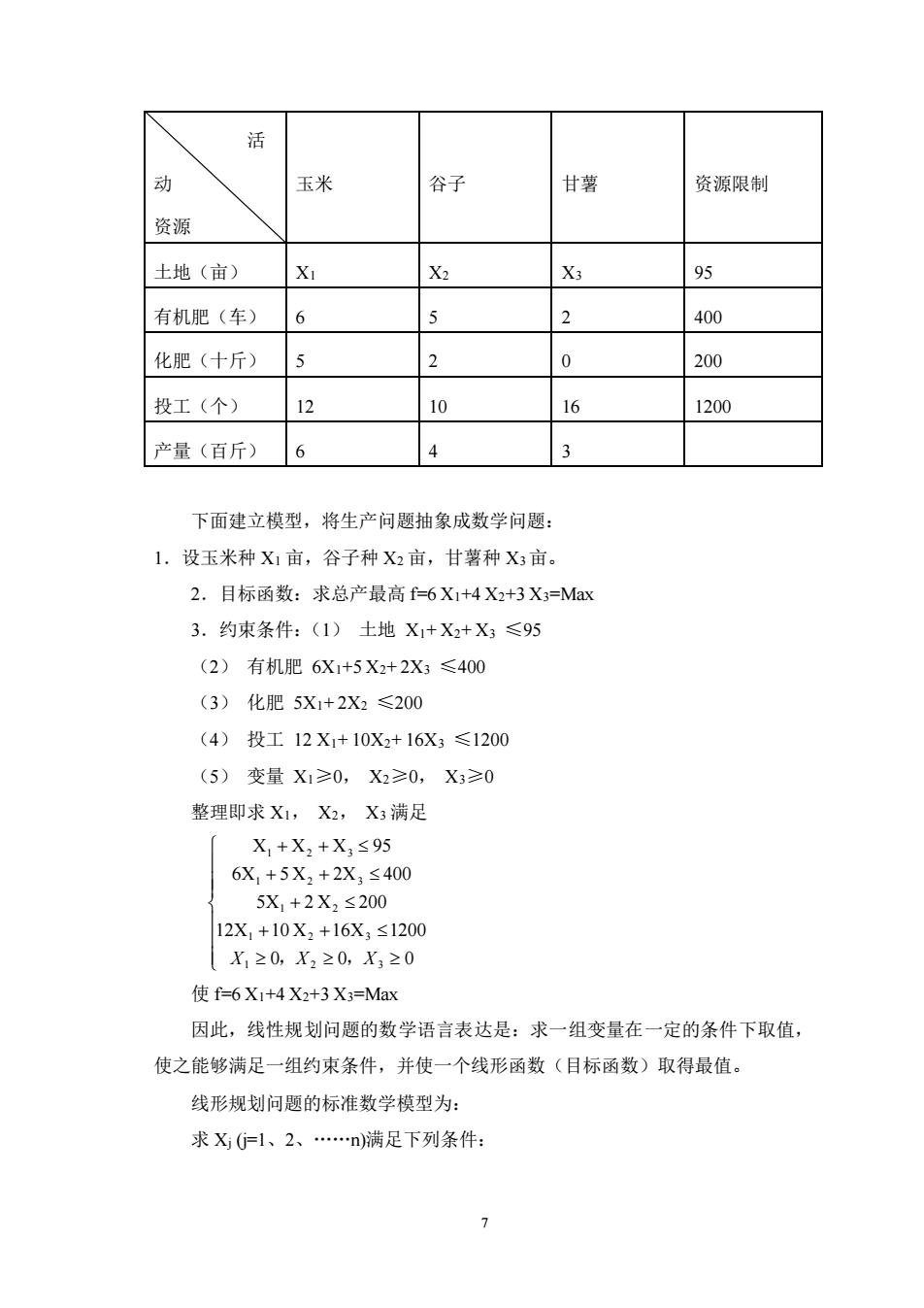
活 动 玉米 谷子 甘薯 资源限制 资源 土地(亩) X2 X3 95 有机肥(车) 6 2 400 化肥(十斤) 5 2 0 200 投工(个) 12 10 16 1200 产量(百斤) 6 3 下面建立模型,将生产问题抽象成数学问题: 1.设玉米种X1亩,谷子种X2亩,甘薯种X3亩。 2.目标函数:求总产最高-6X1+4X2+3X3=Ma 3.约束条件:(1)土地X1+X2+X3≤95 (2)有机肥6X1+5X2+2X3≤400 (3)化肥5X1+2X2≤200 (4)投工12X1+10X2+16X3≤1200 (5)变量X1≥0,X2≥0,X3≥0 整理即求X1,X2,X3满足 X1+X,+X,≤95 6X,+5X2+2X,≤400 5X,+2X,≤200 12X1+10X2+16X3≤1200 X120,X220,X3≥0 使f=6X1+4X2+3X3=Max 因此,线性规划问题的数学语言表达是:求一组变量在一定的条件下取值, 使之能够满足一组约束条件,并使一个线形函数(目标函数)取得最值。 线形规划问题的标准数学模型为: 求X心=1、2、n)满足下列条件 1
7 活 动 资源 玉米 谷子 甘薯 资源限制 土地(亩) X1 X2 X3 95 有机肥(车) 6 5 2 400 化肥(十斤) 5 2 0 200 投工(个) 12 10 16 1200 产量(百斤) 6 4 3 下面建立模型,将生产问题抽象成数学问题: 1.设玉米种 X1 亩,谷子种 X2 亩,甘薯种 X3亩。 2.目标函数:求总产最高 f=6 X1+4 X2+3 X3=Max 3.约束条件:(1) 土地 X1+ X2+ X3 ≤95 (2) 有机肥 6X1+5 X2+ 2X3 ≤400 (3) 化肥 5X1+ 2X2 ≤200 (4) 投工 12 X1+ 10X2+ 16X3 ≤1200 (5) 变量 X1≥0, X2≥0, X3≥0 整理即求 X1, X2, X3 满足 + + + + + + + 0 0 0 12X 10 X 16X 1200 5X 2 X 200 6X 5 X 2X 400 X X X 95 1 2 3 1 2 3 1 2 1 2 3 1 2 3 X ,X ,X 使 f=6 X1+4 X2+3 X3=Max 因此,线性规划问题的数学语言表达是:求一组变量在一定的条件下取值, 使之能够满足一组约束条件,并使一个线形函数(目标函数)取得最值。 线形规划问题的标准数学模型为: 求 Xj (j=1、2、.n)满足下列条件:
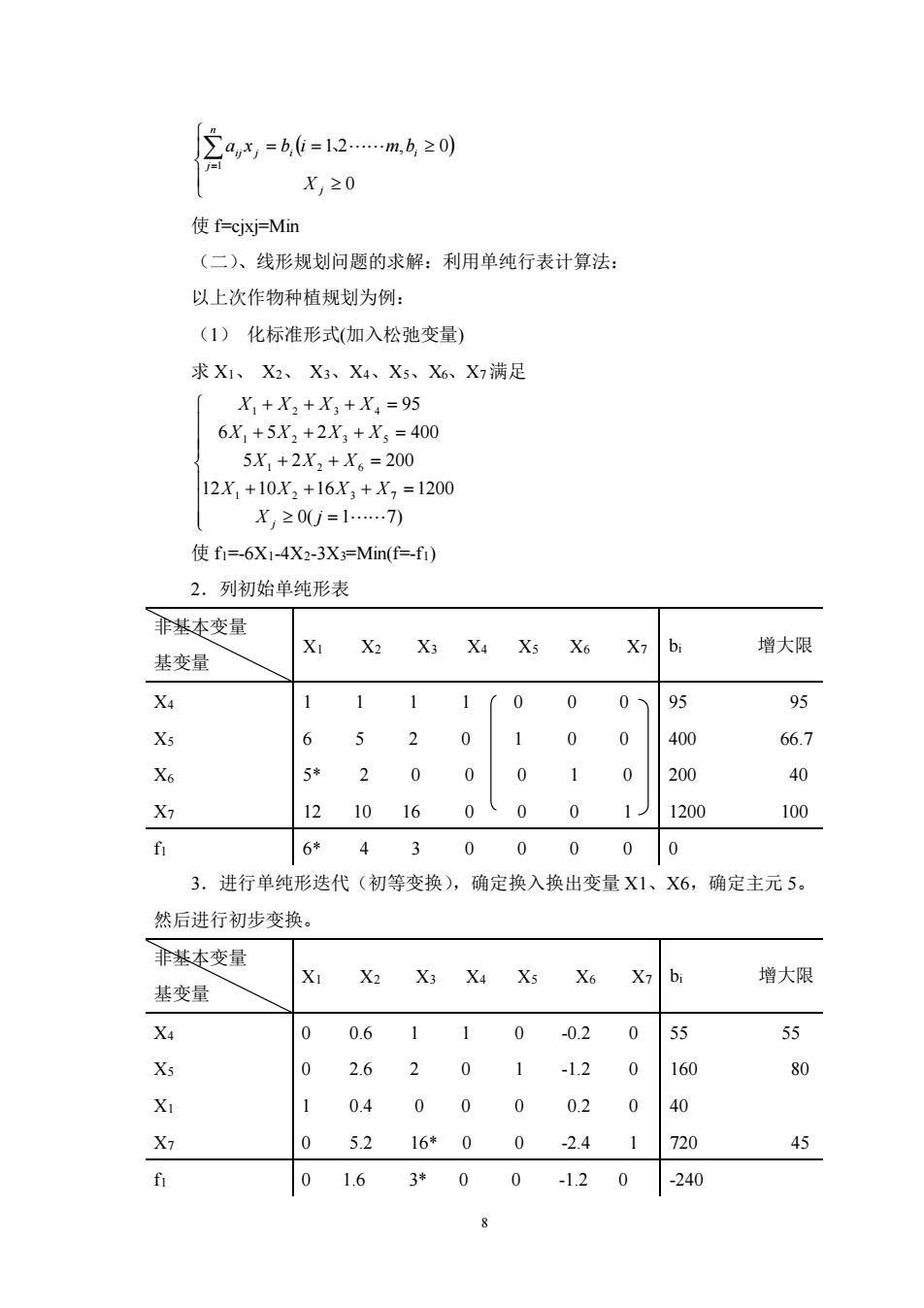
2ax,=b6=12.m.620) X,≥0 使f=cjxj=Mim (二)、线形规划问题的求解:利用单纯行表计算法: 以上次作物种植规划为例: (1)化标准形式(加入松弛变量) 求X1、X2、X3、X4、X5、X6、X7满足 X+X2+X,+X=95 6X,+5X2+2X3+X5=400 5X1+2X2+X。=200 12X1+10X2+16X3+X7=1200 X,≥0U=1小.7 fi=-6X1-4X2-3X3=Min(f=-fi) 2.列初始单纯形表 非基本变量 X 七 X: 增大限 基变量 10 0 0 95 8 6 5 2 0 0 0 400 66.7 X6 2 0 0 0 1 0 200 % X7 12101600 0 1 1200 100 6 430 00 0 0 3.进行单纯形选代(初等变换),确定换入换出变量X1、X6, 确定主元5。 然后进行初步变换。 非基本变量 XI X2 X3 X4 X5 X6 增大限 基变量 X4 0 0.6 110 -0.2 0 55 55 Xs 0 2.6 2 0 1 -1.2 0 160 80 X 1 0.4000 0.2 40 X7 05.216*00-2.41 720 45 0 1.6 3*00-120 -240
8 ( ) = = = 0 1 2 , 0 1 j n j ij j i i X a x b i 、m b 使 f=cjxj=Min (二)、线形规划问题的求解:利用单纯行表计算法: 以上次作物种植规划为例: (1) 化标准形式(加入松弛变量) 求 X1、 X2、 X3、X4、X5、X6、X7满足 = + + + = + + = + + + = + + + = 0( 1 7) 12 10 16 1200 5 2 200 6 5 2 400 95 1 2 3 7 1 2 6 1 2 3 5 1 2 3 4 X j X X X X X X X X X X X X X X X j 使 f1=-6X1-4X2-3X3=Min(f=-f1) 2.列初始单纯形表 非基本变量 基变量 X1 X2 X3 X4 X5 X6 X7 bi 增大限 X4 X5 X6 X7 1 1 1 1 0 0 0 6 5 2 0 1 0 0 5* 2 0 0 0 1 0 12 10 16 0 0 0 1 95 95 400 66.7 200 40 1200 100 f1 6* 4 3 0 0 0 0 0 3.进行单纯形迭代(初等变换),确定换入换出变量 X1、X6,确定主元 5。 然后进行初步变换。 非基本变量 基变量 X1 X2 X3 X4 X5 X6 X7 bi 增大限 X4 X5 X1 X7 0 0.6 1 1 0 -0.2 0 0 2.6 2 0 1 -1.2 0 1 0.4 0 0 0 0.2 0 0 5.2 16* 0 0 -2.4 1 55 55 160 80 40 720 45 f1 0 1.6 3* 0 0 -1.2 0 -240
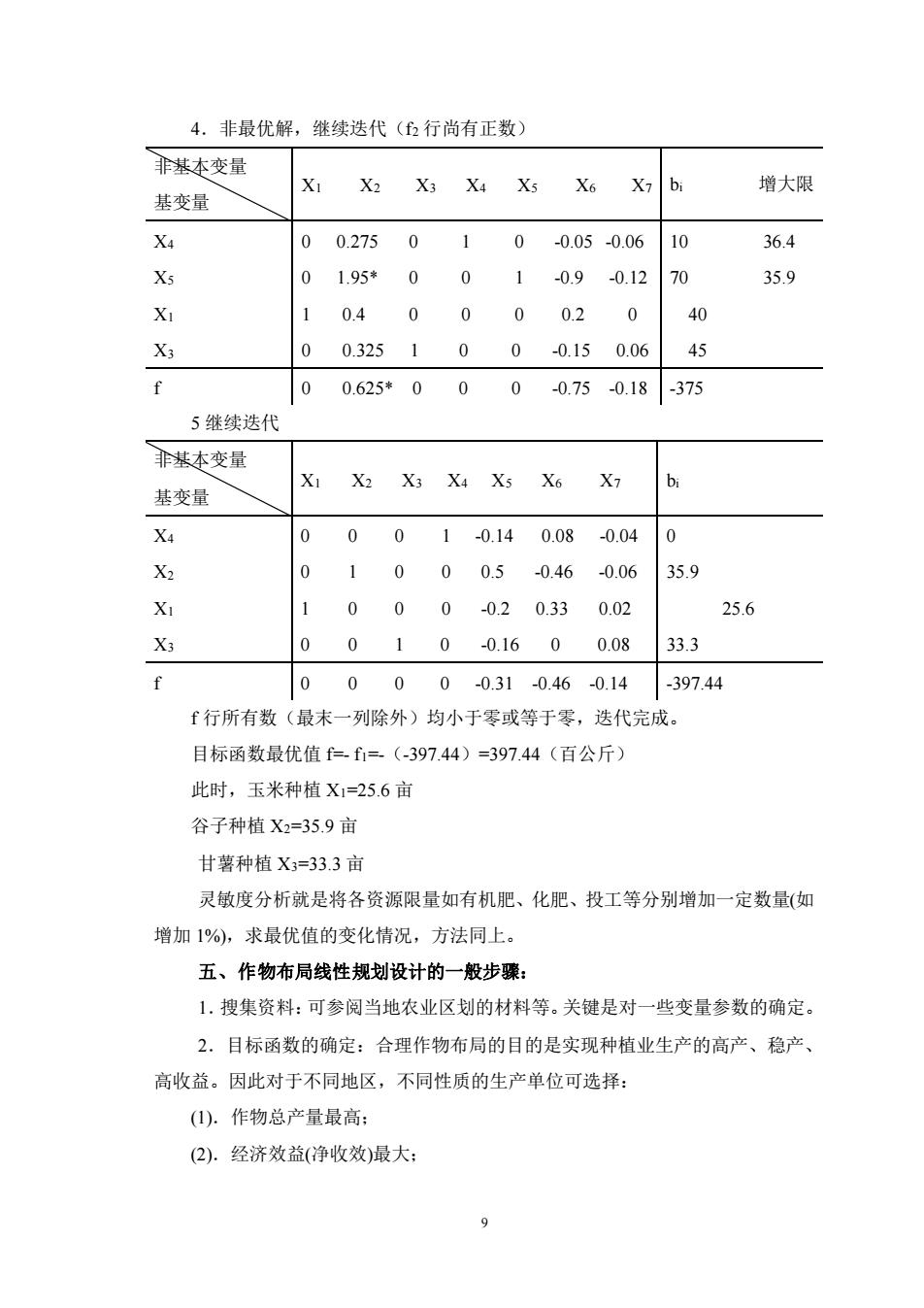
4.非最优解,继续迭代(6行尚有正数) 非基本变量 X X2 X3 X4 X5 X6 b 增大限 基变量 0 0.27501 0-0.050.06 10 36.4 七 0 1.95*001-0.90.12 70 35.9 0.40000.2 0 % X; 00.3251 00-0.150.06 45 0 0.625*000-0.750.18-375 5继续迭代 基枣变量 X X> 基变量 X3 X4 X5 X6 Xa 0 001-0.140.08-0.040 X2 1 0 00.5 -0.46 0.06 35.9 000-020.33 0.02 25.6 X3 0010-0.1600.0833.3 00 00-0.31-0.46-0.14 -397.44 「行所有数(最末一列除外)均小于零或等于零,迭代完成。 目标函数最优值仁f=(-397.44)=397.44(百公斤) 此时,玉米种植X1=25.6亩 谷子种植X2=35.9亩 甘薯种植X3=33.3亩 灵敏度分析就是将各资源限量如有机肥、化肥、投工等分别增加一定数量(如 增加1%),求最优值的变化情况,方法同上。 五、作物布局线性规划设计的一般步骤 1.搜集资料:可参阅当地农业区划的材料等。关键是对一些变量参数的确定。 2.目标函数的确定:合理作物布局的目的是实现种植业生产的高产、稳产、 高收益。因此对于不同地区,不同性质的生产单位可选择: ().作物总产量最高: (2).经济效益(净收效)最大: 9
9 4.非最优解,继续迭代(f2 行尚有正数) 非基本变量 基变量 X1 X2 X3 X4 X5 X6 X7 bi 增大限 X4 X5 X1 X3 0 0.275 0 1 0 -0.05 -0.06 0 1.95* 0 0 1 -0.9 -0.12 1 0.4 0 0 0 0.2 0 0 0.325 1 0 0 -0.15 0.06 10 36.4 70 35.9 40 45 f 0 0.625* 0 0 0 -0.75 -0.18 -375 5 继续迭代 非基本变量 基变量 X1 X2 X3 X4 X5 X6 X7 bi X4 X2 X1 X3 0 0 0 1 -0.14 0.08 -0.04 0 1 0 0 0.5 -0.46 -0.06 1 0 0 0 -0.2 0.33 0.02 0 0 1 0 -0.16 0 0.08 0 35.9 25.6 33.3 f 0 0 0 0 -0.31 -0.46 -0.14 -397.44 f 行所有数(最末一列除外)均小于零或等于零,迭代完成。 目标函数最优值 f=- f1=-(-397.44)=397.44(百公斤) 此时,玉米种植 X1=25.6 亩 谷子种植 X2=35.9 亩 甘薯种植 X3=33.3 亩 灵敏度分析就是将各资源限量如有机肥、化肥、投工等分别增加一定数量(如 增加 1%),求最优值的变化情况,方法同上。 五、作物布局线性规划设计的一般步骤: 1.搜集资料:可参阅当地农业区划的材料等。关键是对一些变量参数的确定。 2.目标函数的确定:合理作物布局的目的是实现种植业生产的高产、稳产、 高收益。因此对于不同地区,不同性质的生产单位可选择: (1).作物总产量最高; (2).经济效益(净收效)最大;