
2.3。随机变量函数的分布 离散型随机变量函数的概率分布 g(X)g(x)g(x) g(Xn) P2 Pn 注意 离散型随机变量函数的概率分布分以下两步来求: (1)由yg(x)计算出随机变量Y的所有取值y1y2,yn, (2)P(Yyn)为yn对应的随机变量X的取值的概率和
注意 离散型随机变量函数的概率分布分以下两步来求: (1)由y=g(x)计算出随机变量Y的所有取值y1 ,y2 ,...,yn ,...; (2)P(Y=yn )为yn 对应的随机变量X的取值的概率和. X x1 x2 ... xn ... g(X) g(x1 ) g(x2 ) … g(xn ) … P p1 p2 ... pn ... 离散型随机变量函数的概率分布: 2.3. 随机变量函数的分布

连续型随机变量函数的概率密度函数 定理1 设Xfx(x),y=g(x)是x的单调可导函数,其导数不为0 值域为(a,b),-oo<a<b<+o,记x-h(y)为y-g(x)的反函数,则 Y=gX)的概率密度函数为 fx[h(y)h'(y) a<y<b fy(y)= 0 其它
定理1 设X~fX(x),y=g(x)是x的单调可导函数,其导数不为0, 值域为(a,b),-∞<a<b<+∞,记x=h(y)为y=g(x)的反函数,则 Y=g(X)的概率密度函数为: = 0 其它 f [ h( y )] | h ( y )| a y b f ( y ) X Y 连续型随机变量函数的概率密度函数

第3拿 随机向量 ·随机向量及其概率分布 ·随机向量的联合分布函数 随机变量函数的分布
第3章 随机向量 •随机向量及其概率分布 •随机向量的联合分布函数 •随机变量函数的分布

第3.1节 随机向量及其概率分布 例如射击一次.问击中否?击中几环?击中点的坐标?击中 点到靶心的距离? 1.n维随机向量 以n个随机变量X1,X2,…,X为分量的向量 X=(X,X2,…,Xn)称为n维随机向量 以下主要研究二维离散型及连续型随机向量的情形。 2.二维离散型随机向量的联合概率分布、边缘概率分布 定义如果二维随机向量(X,Y)的全部取值数对为有限 个或至多可列个,则称随机向量(X,Y)为离散型的。 易见,二维随机向量X,Y)为离散型的等价于它的每个分量 X与Y分别都是一维离散型的
1. n 维随机向量 以 n 个随机变量 X1,X2,…,Xn 为分量的向量 X=(X1 ,X2 ,…,Xn )称为n维随机向量。 以下主要研究二维离散型及连续型随机向量的情形。 2. 二维离散型随机向量的联合概率分布、边缘概率分布 定义 如果二维随机向量(X,Y)的全部取值数对为有限 个或至多可列个,则称随机向量(X,Y)为离散型的。 易见,二维随机向量(X,Y)为离散型的等价于它的每个分量 X与Y分别都是一维离散型的。 第3.1节 随机向量及其概率分布 例如射击一次.问击中否?击中几环?击中点的坐标?击中 点到靶心的距离?

联合概率分布 称p,P(X=X,Yy),(i,j=1,2…,)为X,Y)的联合概率分布.其 中E={(y),ij=1,2,}为(仪,Y)的取值集合,表格形式如下: y2 y p11 P12 X2 P21 P22 P2j ●●。 Pi Pi2 ij 。。● 。●● 联合概率分布性质 ①p20;j1,2 ②∑∑P=1; 计算P{X,Y)eD)=∑P, (xiyi)eD
称pij=P(X=xi ,Y=yj ),(i,j=1,2,…,)为(X,Y)的联合概率分布.其 中E={(xi ,yj ),i,j=1,2,...}为(X,Y)的取值集合,表格形式如下: X x1 x2 … x i … y1 y2 … y j … p11 p12 … p1j … p21 p22 … p2j … … … … … … pi1 pi2 … p i j … … … … … … Y 计算P{(X,Y)∈D }= x y D ij i j p ( ) , 联合概率分布性质 ① pij≥0 ;i,j=1,2,… ②∑∑pij = 1; 联合概率分布

边缘概率分布 (1)定义随机向量X=(X1,X2,…,X)中每一个X,的分布, 称为X关于X的边缘分布。 (2)边缘分布列 对于离散型随机向量X,Y),分量X,Y的分布列称为 边缘分布列 若X,Y)的联合概率分布为pP{(X=x,Y=y),ij户1,2,,则 P(X=x)=P(X=x)Y=(i=1,2....) ∑P(X=x)n=》=∑P(X=Y=y,)=∑P, = 同理 PY=y,)=∑P (=1,2,) 般地,记:PX=x) P(Y=y) 概率分布表如下:
(1) 定义 随机向量X=(X1 ,X2 ,…,Xn)中每一个Xi的分布, 称为X关于Xi的边缘分布。 (2) 边缘分布列 对于离散型随机向量(X,Y),分量X,Y的分布列称为 边缘分布列。 若(X,Y)的联合概率分布为pij=P{X=xi ,Y=yj ),i,j=1,2,...,则 ( ) {( ) [ ( )]} i i j j P X x P X x Y y = = = = {( ) ( )} i j j = = = P X x Y y ( , ) i j j = = = P X x Y y = j ij p (i=1,2,...) 同理 ( )j ij i P Y y p = = 一般地,记: P(X=xi ) Pi . P(Y=yj ) P. j (j=1,2,...) 概率分布表如下: 边缘概率分布

Y y…y…Pa Xj P11P12…P1y· Pu. X2 P21P22…P2j P2. Xi p1p2…P : p1p.2…卫
X Y . j y y y 1 2 x i xx 21 i1 i2 i j 2 1 2 2 2 j 1 1 1 2 1 j p p p p p p p p p Pi .2 . 1 . i ppp P. j p.1 p.2 p. j

独立性若X,Y)的联合概率分布满足 PX=xi,Y-y)=PX-xi)P(Y=yi) 称X与Y独立。 例1某盒子中有形状相同的2个白球,3个黑球。从中 一个个取球,令 第次取白球 i=1,2 第次取黑球 分放回或不放回情形 求:(1)Y,Y,)的联合概率分布, (2)边缘概率分布 (3)讨论Y与Y的独立性
独立性 若(X,Y)的联合概率分布满足 P{X=xi ,Y=yj )=P(X=xi )P(Y=yj ) 称X与Y独立。 例1 某盒子中有形状相同的2个白球, 3个黑球。从中 一个个取球,令 (3) Y Y 。 (2) ; : (1)(( Y , Y ) ; i 1,2 0 i 1 i Y 1 2 1 2 i 讨 论 与 的独立性 边缘概率分布 求 的联合概率分布 分放回或不放回情形 第 次取黑球 第 次取白球 = =
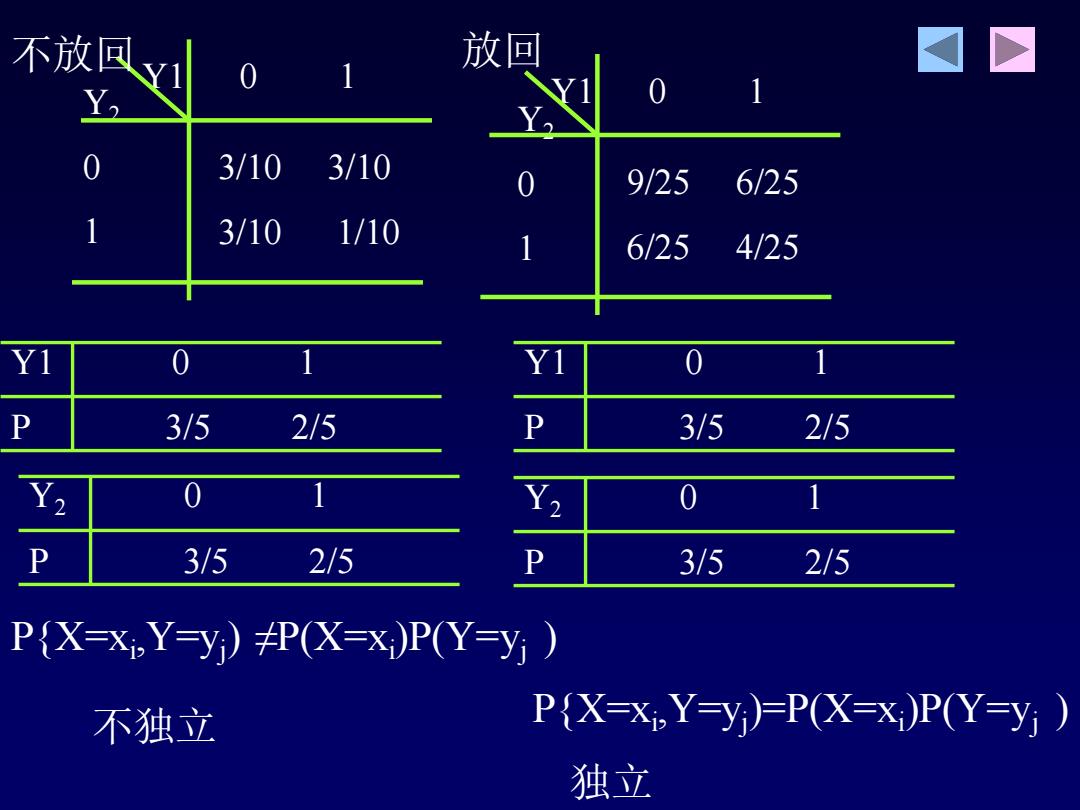
不放回 y 0 1 放回 Y 3/10 3/10 9/25 6/25 3/10 1/10 6/254/25 YI 0 1 0 1 P 3/5 2/5 P 3/5 2/5 Y 0 1 Y 0 1 P 3/52/5 P 3/5 2/5 PX=xi,Y=y)P(X-x)P(Y=y 不独立 P{X=X,Yy尸PX=xP(Y=y) 独立
Y2 0 1 Y1 0 1 3/10 3/10 3/10 1/10 Y1 0 1 P 3/5 2/5 Y2 0 1 P 3/5 2/5 Y1 0 1 P 3/5 2/5 Y2 0 1 P 3/5 2/5 Y2 0 1 Y1 0 1 9/25 6/25 6/25 4/25 不放回 放回 P{X=xi ,Y=yj ) ≠P(X=xi )P(Y=yj ) 不独立 独立 P{X=xi ,Y=yj )=P(X=xi )P(Y=yj )
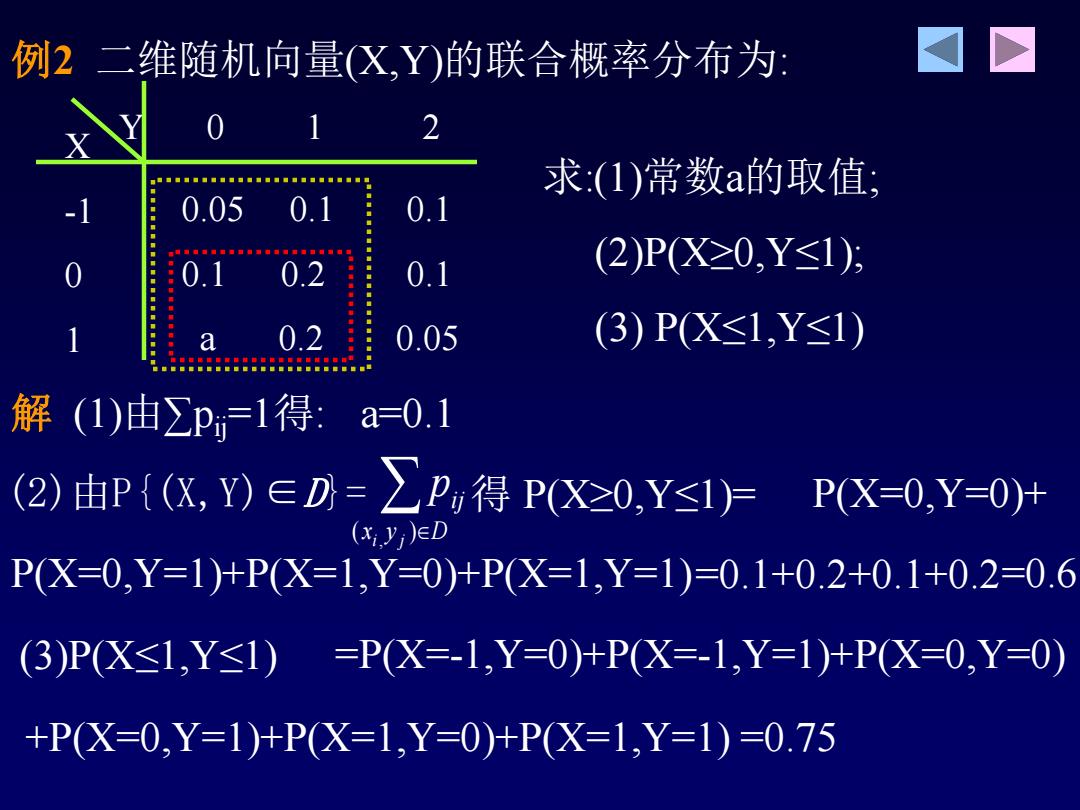
例2二维随机向量X,Y)的联合概率分布为: 求:(1)常数a的取值: 0.05 0.1 0.1 0.1 0.2 0.1 (2)PX20,Y≤1)月 0.05 (3)PX≤1,Y≤1) 解(1)由2P,1得: a=0.1 (2)P{(X,Y)∈D=∑P,得PX0,Y≤1)= PX=0,Y=0)+ (xiyi)ED PX=0,Y=1)+PX=1,Y=0)+PX=1,Y=1)=0.1+0.2+0.1+0.2=0.6 (3)P(X≤1,Y≤1) =PX=-1,Y=0)+P(X=-1,Y=1)+PX=0,Y=0) +PX=0,Y=1)+PX=1,Y=0)+PX=1,Y=1)=0.75
例2 二维随机向量(X,Y)的联合概率分布为: X -1 0 1 Y 0 1 2 0.05 0.1 0.1 0.1 0.2 0.1 a 0.2 0.05 求:(1)常数a的取值; (2)P(X≥0,Y≤1); (3) P(X≤1,Y≤1) 解 (1)由∑pij=1得: a=0.1 (2)由P{(X,Y)∈D}= x y D ij i j p ( ) , 得 P(X≥0,Y≤1)= P(X=0,Y=0)+ P(X=0,Y=1)+P(X=1,Y=0)+P(X=1,Y=1)=0.1+0.2+0.1+0.2=0.6 (3)P(X≤1,Y≤1) =P(X=-1,Y=0)+P(X=-1,Y=1)+P(X=0,Y=0) +P(X=0,Y=1)+P(X=1,Y=0)+P(X=1,Y=1) =0.75