第5章极限定理初步 5.1内容框图 大数定理 中心极限定理 辛软大数定理 贝努里大数定理 林德贝格一列维极限定理 德莫哇佛一拉普拉斯极限定理 应用 5.2基本要求 (1)了解贝努里大数定理和辛钦大数定理 (2)理解并掌握独立同分布的中心极限定理及二项分布的中心极限定理. 5.3内容概要 1)大数定理 概率论中用来阐明随机试验的平均结果具有稳定性的一系列定理都叫大数定理,这里大 数指试验次数足够多,试验的平均结果用随机变量表示就是∑ 5:,那么稳定性是指稳定 在哪里呢?当然是稳定在它的期望值 而稳定的含义就是以概率收敛,即一定 条件下有:对任意£>0, P三-之小1将迪:当立E相时 分布(=1,2,…)且期望有限时,就得到辛钦大数定理 93
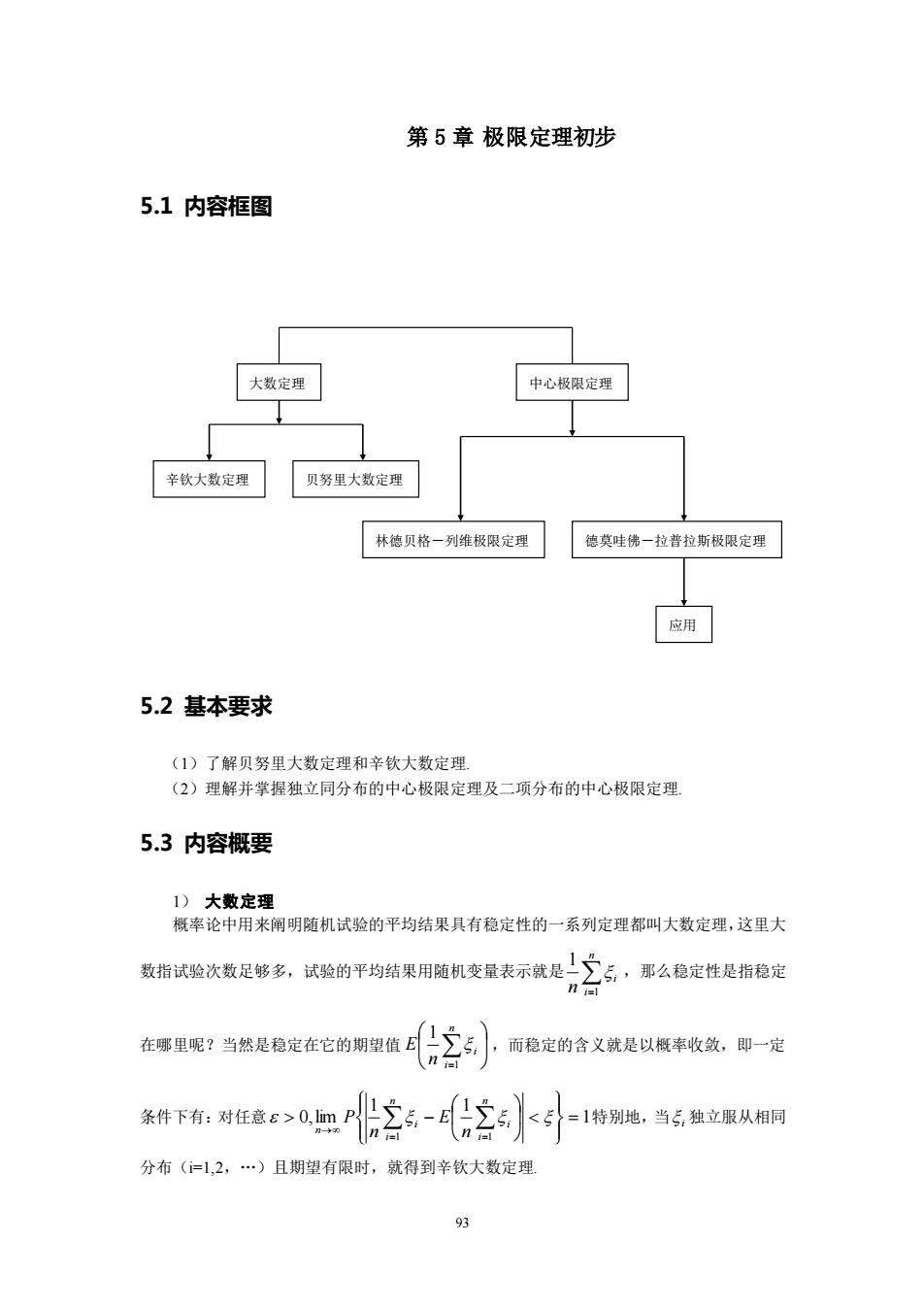
93 第 5 章 极限定理初步 5.1 内容框图 5.2 基本要求 (1)了解贝努里大数定理和辛钦大数定理. (2)理解并掌握独立同分布的中心极限定理及二项分布的中心极限定理. 5.3 内容概要 1) 大数定理 概率论中用来阐明随机试验的平均结果具有稳定性的一系列定理都叫大数定理,这里大 数指试验次数足够多,试验的平均结果用随机变量表示就是 = n i i n 1 1 ,那么稳定性是指稳定 在哪里呢?当然是稳定在它的期望值 = n i i n E 1 1 ,而稳定的含义就是以概率收敛,即一定 条件下有:对任意 1 1 1 0,lim 1 1 = − = = → n i n i i i n n E n P 特别地,当 i 独立服从相同 分布(i=1,2,…)且期望有限时,就得到辛钦大数定理. 大数定理 中心极限定理 辛钦大数定理 贝努里大数定理 林德贝格-列维极限定理 德莫哇佛-拉普拉斯极限定理 应用

当5相互独立且服从相同的两点分布时,得到的就是贝努里大数定理 贝努里大数定理 设4,是在n次独立重复试验(n重贝努里试验)中辜件A发生的次数,p=P(A)是 每次试验时事件A发生的概率,则对任何ε>0,有 贝努里大数定理表明,频率作为概率的近似。 辛钦大数定理 设51,52,…,5m,…是相互独立的服从同一分布的随机变量序列,它们的数学期望是一 个有限值E5=4(i=1,2,…),则对任何8>0,有 贝努里大数定理是辛钦大数定理的特例,辛钦大数定理是贝努里大数定理的推广。 2)中心极限定理 中心极限定理就是用来阐述,一定条件下大量的随机变量的和近似服从正态分布的一系 列定理即和的标准化近似服从标准正态分布 2-42 N0,1). ② 我们在求解有关中心极限定理的各类问题时,主要是用到上面的这个式子特别地,当: (=1,2,…)独立同分布且E5,=μ,D5=02时,上式可化简为 2 ~N(0,1) √no 这就是林德贝格列维中心极限定理 当5,相互独立且都服从两点分布P{5,=1}=p,P{5,=0}=1一p时,上式可简化为 un -np -N(0,) np(1-p) g
94 当 i 相互独立且服从相同的两点分布时,得到的就是贝努里大数定理. 贝努里大数定理 设 n 是在 n 次独立重复试验( n 重贝努里试验)中事件 A 发生的次数, p = P(A) 是 每次试验时事件 A 发生的概率,则对任何 0 ,有 lim =1 − → p n P n n 。 贝努里大数定理表明,频率作为概率的近似。 辛钦大数定理 设 1 , 2 , , n , 是相互独立的服从同一分布的随机变量序列,它们的数学期望是一 个有限值 E i = ( i = 1,2, ),则对任何 0 ,有 1 1 lim 1 = − = → n i i n n P 。 贝努里大数定理是辛钦大数定理的特例,辛钦大数定理是贝努里大数定理的推广。 2) 中心极限定理 中心极限定理就是用来阐述,一定条件下大量的随机变量的和近似服从正态分布的一系 列定理.即和的标准化近似服从标准正态分布. ~ (0,1) 1 1 1 N D E n i i n i n i i i − = = = . 我们在求解有关中心极限定理的各类问题时,主要是用到上面的这个式子.特别地,当 i (i=1,2,…)独立同分布且 E i =μ,D 1 =σ2 时,上式可化简为 ~ (0,1) 1 N n n i i = 这就是林德贝格列维中心极限定理. 当 i 相互独立且都服从两点分布 P{ i =1}=p,P{ i =0}=1-p 时,上式可简化为 ( ) ~ (0,1) 1 N np p np n − −
这就是二项分布的中心极限定理 在概率论中还有其他许多的中心极限定理.求解有关中心极限定理问题的关键就是要凑 出上面的式子(参见本章5.2节例2), 林德贝格一列维中心极限定理(独立同分布中心极限定理) 设51,52,…,5,…是相互独立的服从同一分布的随机变量序列,它们的数学期望和方 差都存在,分别为E5,=4和D5,=o2>0(i=1,2,…),则对任何x,当n→∞时, 有 2 ≤X V2元1ed山=). 当n充分大时,近似有 2-u -≈N(0,1)。 ng? 德莫哇佛一拉普拉斯极限定理(二项分布中心极限定理) 若4n是n次独立重复试验(n重贝努里试验)中事件A发生的次数,0<p<1是事件 1在每次试验中发生的概率,g=1-P,p付)=。 x e2,则 J2π (1)对任意的有限区间[a,1,当a<-吧≤b及n→∞时,有 npq Piun=k Cpgk lim lim- 1 k-np 1→0 1 -p2-1, 2npq npqnpq 2mpq (2)对任何x,当n→oo时,有 ImP4。~p → ≤x7= npq 4n-吧一N0,)。 npq 95
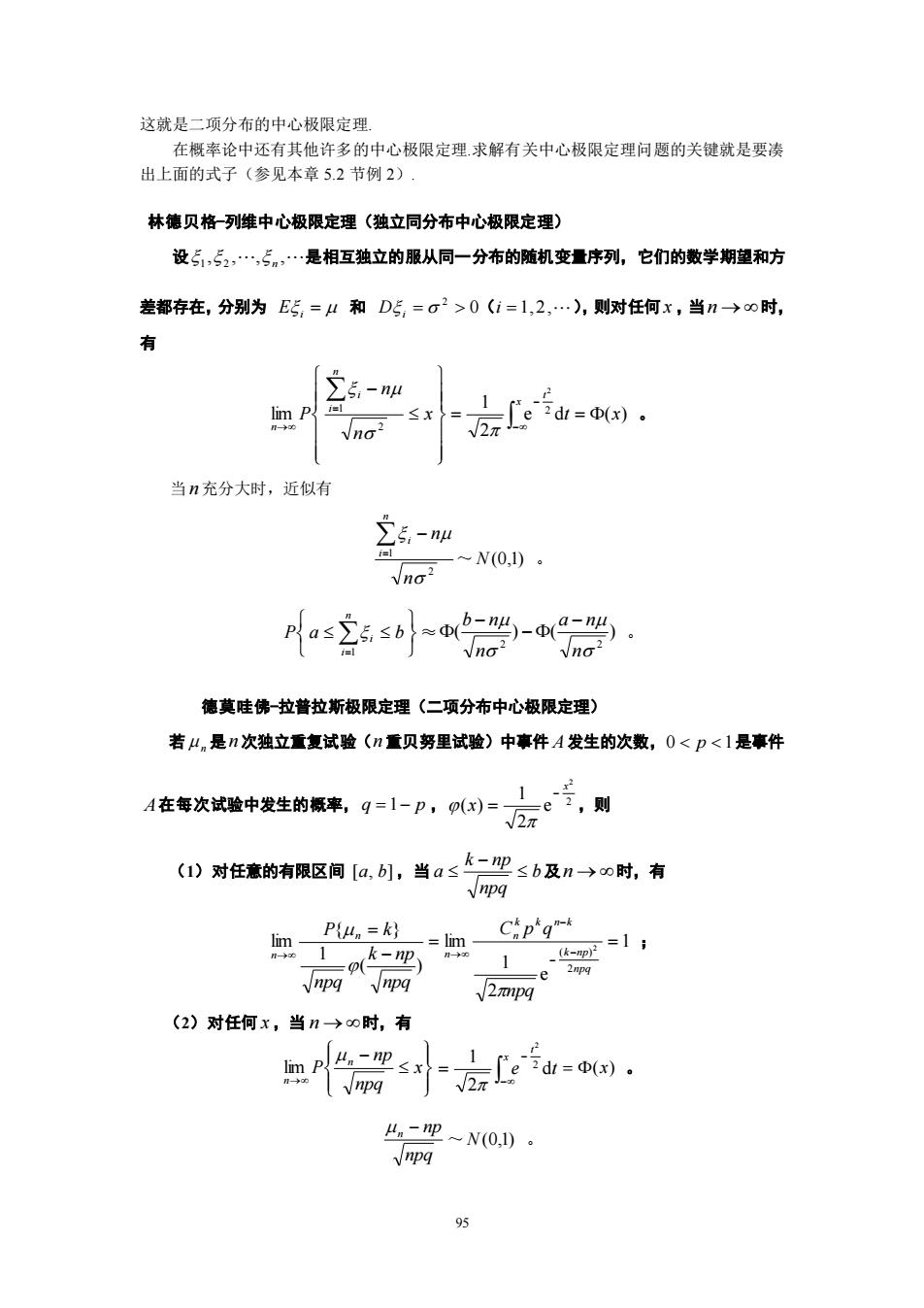
95 这就是二项分布的中心极限定理. 在概率论中还有其他许多的中心极限定理.求解有关中心极限定理问题的关键就是要凑 出上面的式子(参见本章 5.2 节例 2). 林德贝格-列维中心极限定理(独立同分布中心极限定理) 设 1 , 2 , , n , 是相互独立的服从同一分布的随机变量序列,它们的数学期望和方 差都存在,分别为 E i = 和 0 2 D i = ( i = 1,2, ),则对任何 x ,当 n → 时, 有 e d ( ) 2 1 lim 2 2 1 2 x t x n n P x t n i i n = = − − − = → 。 当 n 充分大时,近似有 2 1 n n n i i − = ~ N(0,1) 。 = P a b n i i 1 ≈ ( ) ( ) 2 2 n a n n b n − − − 。 德莫哇佛-拉普拉斯极限定理(二项分布中心极限定理) 若 n 是 n 次独立重复试验( n 重贝努里试验)中事件 A 发生的次数, 0 p 1 是事件 A 在每次试验中发生的概率, q = 1− p , 2 2 e 2 1 ( ) x x − = ,则 (1)对任意的有限区间 [a, b] ,当 b npq k np a − 及 n → 时,有 = − = → ( ) 1 { } lim npq k np npq P k n n 1 e 2 1 lim 2 ( ) 2 = − − − → npq k np k k n k n n npq C p q ; (2)对任何 x ,当 n → 时,有 − → x npq np P n n lim − − = x t e dt 2 1 2 2 = (x) 。 npq np n − ~ N(0,1)

德莫哇佛一拉普拉斯极限定理的一些应用 用正态分布近似计算二项分布的概率: PE≤对≈=),Pa≤5≤b≈(b-吗)-Φ-四)。 npa npq npg 5.4自测题五 一、判断题(正确用“+”,错误用“一”) 1.设5,52,…5,…为一列相互独立的且均服从参数入=3的指数分布的随机变量,则 ▣2--0 >0) () 2.把一枚硬币抛n次,只要n充分大,正面向上发生的频率与0.5的误差就可以小于任意给 定的一个正数& () 3.设4n为n重贝努里试验中事件A发生的次数,p为事件A每次发生的概率,则当n充分 大时,有 台-小小--同司 () 4.把一枚硬币连抛2000次,根据中心极限定理,出现正面向上不超过1000次的概率约为 中0等于2 () 5.设,相互独立且5U1,)仁12,则m之=0 () m→on i=l 6.设为n重贝努里试验中事件A发生的次数,则当n很大时,近似服从正态分布. () 7.设儿,为抛一个骰子n次出现点数为5的次数,则m凸= () nn 6 8.设5,服从参数为入的普阿松分布,5,相互独立,则当n很大时, 之5近似服从正态分布 N(n,n22) () 9n重贝努里试验中,当n充分大时,事件A发生的频率与其发生的概率p的误差不超过' 的概率约为2l/Vp1-p)-1 () 号
96 德莫哇佛-拉普拉斯极限定理的一些应用 用正态分布近似计算二项分布的概率: P{ x}≈ ( ) npq x − np , P{a b}≈ ( ) ( ) npq a np npq b np − − − 。 5.4 自测题五 一、 判断题(正确用“+”,错误用“-”) 1. 设 1 , 2 ,… n ,…为一列相互独立的且均服从参数λ=3 的指数分布的随机变量,则 0 3 1 1 lim 1 = − = → n i i n n P ( 0) . ( ) 2. 把一枚硬币抛 n 次,只要 n 充分大,正面向上发生的频率与 0.5 的误差就可以小于任意给 定的一个正数 . ( ) 3. 设 n 为 n 重贝努里试验中事件 A 发生的次数,p 为事件 A 每次发生的概率,则当 n 充分 大时,有 ( ) − − − p p n p n P n 1 2 1 . ( ) 4. 把一枚硬币连抛 2000 次,根据中心极限定理,出现正面向上不超过 1000 次的概率约为 Φ(0)等于 2 1 . ( ) 5. 设 i 相互独立且 i ~∪(-1,1) (i=1,2,…),则 0 1 lim 1 = = → n i i n n . ( ) 6. 设 为 n 重贝努里试验中事件 A 发生的次数,则当 n 很大时, 近似服从正态分布. ( ) 7. 设 5 n 为抛一个骰子 n 次出现点数为 5 的次数,则 6 1 lim 5 = → n n n . ( ) 8. 设 i 服从参数为λ的普阿松分布, i 相互独立,则当 n 很大时, = n i i 1 近似服从正态分布 ( ) 2 2 N n,n . ( ) 9. n 重贝努里试验中,当 n 充分大时,事件 A 发生的频率与其发生的概率 p 的误差不超过 n 1 的概率约为 2(1/ np(1− p))−1 . ( )

二、选择题 1.设4n为n次独立重复试验中事件A出现的次数,p是事件A在每次试验中出现的概率, e为大于零的数, 则 (A)0 (B)1 ()2 2.设5,52,…独立同服从于指数分布E(入),则( )正确 26-m (A)lim P i=l -≤x=Φ(x) (B)lim P i= ≤x=(x) n n - 5- (C)lim P ≤x =(x) (D)lim P i=l ≤x=D(x) √nz 3.设4n为n次独立重复试验中事件A出现的次数,p为事件A在每次试验中出现的概率, q=1-p,6为大于零的数, 则P怡- wm同1@-网】 (C)1 (D)0 4.设5U(-1,1)=1,2,)且相互独立,则()是不正确的 (A)5i,52,…5n,…序列服从大数定理 (B)51,52,…5m,…序列服从中心极限定理 (C) lim i=l 0)(D)m15=0 →on 5.设5,P(入)=1,2,)且相互独立,则对8>0有(). 97
97 二、 选择题 1. 设 n 为 n 次独立重复试验中事件 A 出现的次数,p 是事件 A 在每次试验中出现的概率, ε为大于零的数,则 = − → p n P n n lim ( ). (A) 0 (B) 1 (C) 2 1 (D) 2 −1 pq n 2. 设 1 , 2 ,…独立同服从于指数分布 E(λ),则( )正确. (A) x (x) n n P n i i n = − = → 1 lim (B) x (x) n n P n i i n = − = → 1 lim (C) x (x) n P n i i n = − = → 1 lim (D) x (x) n n P n i i n = − = → 1 lim 3. 设 n 为 n 次独立重复试验中事件 A 出现的次数,p 为事件 A 在每次试验中出现的概率, q = 1− p, 为大于零的数,则 − p n P n ( ). (A) 2 −1 pq n (B) − pq n 2 1 (C) 1 (D) 0 4. 设 i ~U(-1,1)(i=1,2,…)且相互独立,则( )是不正确的. (A) 1 , 2 ,… n ,…序列服从大数定理 (B) 1 , 2 ,… n ,…序列服从中心极限定理 (C) lim 1 1 = = → n P n i i n ( 0 ) (D) 0 1 lim 1 = = → n i i n n 5. 设 i ~P(λ)(i=1,2,…)且相互独立,则对 >0 有( )

wPz-1-a叫 B月 -小小网》 (e)r 空-s-叫 Pz-s-40团 ( 1+x -1≤x0有 98
98 (A) − − = n n P n i i 2 1 1 1 (B) ( ) − − − = 1 2 1 1 1 n n P n i i (C) − − = n n P n i i 2 1 1 1 (D) ( ) − − − = 1 2 1 1 1 n n P n i i 6. 设 i 独立同分布,其概率密度均为 ( ) − + = 0 1 1 x x x 其他 0 1 1 0 − x x ,则当 n 充分大时,近似 地有( ). (A) ~ (0,1) 1 N n i i = (B) ~ (0,1) 6 1 N n n i i = (C) ~ (0,1) 1 1 N n n i i = (D) ~ (0,1) 6 1 N n n i i = 7. 设 i (i=1,2,…,100)相互独立,且均服从 P(0.03),则 = 3 1 n i P i ( ) (A) 1-Φ(3) (B) Φ(3) (C) 0.5 (D) 1-Φ(0.03) 8. 设 1 2 100 , ..., 是独立同分布的,且 i ~ b(1, p),则下面不正确的是( ). (A) b( p) i i ~ 100, 100 1 = (B) P a b (b) (a) i i − = 100 1 (C) p i i = 100 100 1 1 (D) ( ) ( ) − − − − − = p p a p p p b p P a b i i 10 1 100 10 1 100 100 1 9. 设 1 , 2 ,… n ,…为一列独立同分布的随机变量,且 E i =0,D i =σ2,则对 0 有

w=P2>=0 m=P20(=1,2…),则对任意e>0,m 5.测量某一长度为a的物体,假定各次测量结果相互独立,且服从正态分布N(a,0.22),若 以Xm表示n次测量结果的平均值,为使P区。-d≤0.1≥0.95,则n应不小于 6.设X,X2,…,Xm,…是相互独立的随机变量序列,且都服从参数为入的普阿松分布, 则当n充分大时, ∑X,近似服从 7.从一大批次品率为0.03的产品中随机抽取1000件该种产品,则其中的次品数X的精确 分布为 :其近似分布为 :若利用德莫哇佛拉普拉斯中心极限定理计算, 则P{20≤X≤40}= 8.某厂产品次品率为1%,今任取500个,则根据中心极限定理估计其中次品不超过5个的 概率为 99
99 ( ). (A) 0 1 lim 1 2 = = → n i i n n P (B) 0 1 lim 1 2 = = → n i i n n P (C) 0 1 lim 1 2 2 = − = → n i i n n P (D) 0 1 lim 1 2 2 = − = → n i i n n P 三、 填空题 1. 设 1 , 2 ,…为相互独立的随机变量序列,且 i (i=1,2…)服从参数为λ的普阿松分布, 记 (x) e dx x x 2 2 2 1 − − = ,则 = − = → x n n P n i i n 1 lim _______. 2. 设ξ表示 n 次独立重复试验中事件 A 出现的次数,p 是事件 A 在每次试验中的出现概率, 记 (x) e dx x x 2 2 2 1 − − = ,则 Pa b _______. 3. 设 X1 , X2 ,…, X n ,…是独立同分布的随机变量序列,且 Xi ~U(0,a)(i=1,2,…).则当 n 充分大时, = = n i Xi n X 1 1 近似服从_______. 4. 设 X1 , X2 , … , X n , … 是 相 互 独 立 同 分 布 的 随 机 变 量 序 列 , 且 ( ) , ( ) 0 2 E Xi = D Xi = (i=1,2,…),则对任意ε>0, = − = → n i i n P X n 1 lim _____. 5. 测量某一长度为 a 的物体,假定各次测量结果相互独立,且服从正态分布 ( ) 2 N a,0.2 ,若 以 X n 表示 n 次测量结果的平均值,为使 PX n − a 0.1 0.95 ,则 n 应不小于_______. 6. 设 X1 , X2 ,…, X n ,…是相互独立的随机变量序列,且都服从参数为λ的普阿松分布, 则当 n 充分大时, = n i Xi 1 近似服从_______. 7. 从一大批次品率为 0.03 的产品中随机抽取 1000 件该种产品,则其中的次品数 X 的精确 分布为________;其近似分布为_______;若利用德莫哇佛 拉普拉斯中心极限定理计算, 则 P{20≤X≤40}=________. 8. 某厂产品次品率为 1%,今任取 500 个,则根据中心极限定理估计其中次品不超过 5 个的 概率为_______

9.设5,52,5n,…独立同分布,且E5=a(k=1,2,3,4),a4≠a匠,则当n充分大时根据 中心极限定理有、 ni= 5.5自测题五答案 一、1.+;2.-:3.+;4.+:5.-:6.+:7.-;8-:9.+ 二、1.B:2.A:3.A:4.D:5.A:6.B:7.C:8.B:9.C b-np a-np 三、1.Φ(x):2.① 3.N aa 4.1:5.15:6.Nnz,n: npg 、npq 212n 5.6典型例题 例1作加法时,对每个加数四舍五入取整,各个加数的取整误差可以认为是相互独立的, 都服从(-0.5,0.5)上的均匀分布。现在有1200个数相加,问取整误差总和的绝对值超过12 的概率是多少? 解设各个加数的取整误差为5(i=1,2,…,1200)。因为5,~U(-0.5,0.5),所 以u=E5,=-05,+05=0,g2=D5=05+05Y= 2 1212 (i=12,1200。 设取整误差的总和为7=∑:,因为n=1200数值很大,由定理5.3可知,这时近似 有7=立5~N0g,a),其中,m=120x0=0,na2=120x7=10· 所以,取整误差总和的绝对值超过12的概率为 P>-1129s2--a 1-[w73-o0-12+-12 100
100 9. 设 1 , 2 ,… n ,…独立同分布,且 ( ) 2 4 2 E ak k 1,2,3,4 ,a a k i = = ,则当 n 充分大时根据 中心极限定理有 ~ 1 1 2 = n i i n _______. 5.5 自测题五答案 一、 1. +;2.-;3.+;4. +;5.-;6. +;7.-;8.-;9.+ 二、 1. B;2. A;3. A;4. D;5. A;6. B;7. C;8. B;9. C 三、 1. Φ(x);2. − − − npq a np npq b np ;3. n a a N 12 , 2 2 ;4. 1;5. 15;6. N(n,n) ; 7. b(1000,0.03),N(30,29.1), 1 0.9356 29.1 10 2 − ;8. 0.5;9. − n a a N a 2 4 2 2 , 5.6 典型例题 例 1 作加法时,对每个加数四舍五入取整,各个加数的取整误差可以认为是相互独立的, 都服从 (−0.5,0.5) 上的均匀分布。现在有 1200 个数相加,问取整误差总和的绝对值超过 12 的概率是多少? 解 设各个加数的取整误差为 i ( i = 1,2, ,1200 )。因为 i ~U(−0.5,0.5) ,所 以 0 2 0.5 0.5 = − + = E i = , 12 1 12 (0.5 0.5) 2 2 = + = D i = ( i = 1,2, ,1200 )。 设取整误差的总和为 = = n i i 1 ,因为 n =1200 数值很大,由定理 5.3 可知,这时近似 有 = = n i i 1 ~ ( , ) 2 N n n ,其中, n = 1200 0 = 0 , 100 12 1 1200 2 n = = 。 所以,取整误差总和的绝对值超过 12 的概率为 P 12 =1− P−12 12≈ − − − − − ) 12 ) ( 12 1 ( 2 2 n n n n − − − − = − ) 100 12 0 ) ( 100 12 0 1 ( = 1− (1.2) + (−1.2)

=2[1-Φ(1.2)]=2×(1-0.8849)=0.2302。 例2某互联网站有10000个相互独立的用户,己知每个用户在平时任一时刻访问该网 站的概率为0.2。求: (1)在任一时刻,有1900~2100个用户访问该网站的概率: (2)在任一时刻,有2100个以上的用户访问该网站的概率。 解这可以看作是一个独立重复试验序列,A={访问网站},A={不访问网站}, p=P(A)=0.2,q=P(A)=1-p=0.8。 设访问网站的用户数为5,显然5服从二项分布,即5~b(n,p)。由于n=10000很 大,由德莫哇佛-拉普拉斯极限定理可知,这时近似有5~N(p,pq),其中 p=10000×0.2=2000,pg=2000×0.8=1600。 (1)有1900~2100个用户访问该网站的概率为 P1900≤5s2100,≈Φ(2100-巴)- 1900-2) npq npq =(210-20)-01900-200 )=Φ(2.5)-(-2.5) √1600 V1600 =2Φ(2.5)-1=2×0.9938-1=0.9876。 (2)有2100个以上的用户访问该网站的概率为 P5>2100,=1-P45≤21001≈1-2100-吧)=1-02100-2000 npq V1600 =1-Φ(2.5)=1-0.9938=0.0062。 例3某车间有200台独立工作的车床,各台车床开工的概率都是0.6,每台车床开 工时要耗电1千瓦。问供电所至少要供给这个车间多少千瓦电力,才能以99.9%的概率保 证这个车间不会因供电不足而影响生产。 解200台车床独立工作,可看作200次独立重复试验,事件A={车床开工},A={ 车床不开工},p=P(A)=0.6,9=P(A)=1-p=0.4。 设5是实际开工的车床数,5~b(n,p),由德莫哇佛-拉普拉斯极限定理可知,这时近 101
101 = 2[1− (1.2)] = 2 (1− 0.8849) = 0.2302 。 例 2 某互联网站有 10000 个相互独立的用户,已知每个用户在平时任一时刻访问该网 站的概率为 0.2。求: (1)在任一时刻,有 1900~2100 个用户访问该网站的概率; (2)在任一时刻,有 2100 个以上的用户访问该网站的概率。 解 这可以看作是一个独立重复试验序列, A = { 访问网站 }, A = { 不访问网站 } , p = P(A) = 0.2, q = P(A) =1− p = 0.8。 设访问网站的用户数为 ,显然 服从二项分布,即 ~b(n, p) 。由于 n =10000 很 大,由 德莫哇 佛- 拉普拉 斯极限 定理 可知, 这时 近似有 ~ N(np , npq) ,其中 np = 10000 0.2 = 2000, npq = 2000 0.8 = 1600。 (1)有 1900~2100 个用户访问该网站的概率为 P{1900 2100}≈ ) 1900 ) ( 2100 ( npq np npq np − − − ) 1600 1900 2000 ) ( 1600 2100 2000 ( − − − = = (2.5) − (−2.5) = 2(2.5) −1 = 20.9938−1= 0.9876 。 (2)有 2100 个以上的用户访问该网站的概率为 P{ 2100} = 1− P{ 2100}≈ ) 2100 1 ( npq − np − ) 1600 2100 2000 1 ( − = − = 1− (2.5) =1−0.9938 = 0.0062 。 例 3 某车间有 200 台独立工作的车床,各台车床开工的概率都是 0.6,每台车床开 工时要耗电 1 千瓦。问供电所至少要供给这个车间多少千瓦电力,才能以 99.9%的概率保 证这个车间不会因供电不足而影响生产。 解 200 台车床独立工作,可看作 200 次独立重复试验,事件 A = { 车床开工 },A = { 车床不开工 }, p = P(A) = 0.6, q = P(A) =1− p = 0.4 。 设 是实际开工的车床数, ~b(n, p) ,由德莫哇佛-拉普拉斯极限定理可知,这时近

似有5~N(p,pg),其中p=200×0.6=120,pg=120×0.4=48。 设b是供给电力的千瓦数,要不影响生产,开工车床数必须小于b,这件事的概率为 P{0≤5≤b}≈Φ( -120)-④0-120 V48 V48 52)--172a29-0-62晨2. 48 48 由题意可知,要有 P0≤5≤6}≈Φb-12 )=0.999, V48 查表可得 6-120=3.0902,所以b=120+3.0902×V48=141.4095。 48 取b=142,即供电142千瓦,就能以99.9%的概率保证这个车间不会因供电不足而影 响生产。换句话说,每天8小时的工作时间中最多只有0.1%的时间,即0.48分钟会受到 影响。 例4设在独立重复试验序列中,每次试验时事件A发生的概率为0.75,分别用 切比雪夫不等式和德莫哇佛-拉普拉斯极限定理估计试验次数需多大,才能使事件A发 生的频率落在0.74~0.76之间的概率至少为0.90。 解 设4,为在n次独立重复试验中事件A发生的次数,么就是A发生的频率。 n (1)用切比雪夫不等式估计。 由于4n~b(n,p),p=0.75,因此E4n=p=0.75n,D4n=npg=0.1875n, 由切比雪夫不等式可得 P0.74≤≤0.76=P4n-0.75n≤0.01m=Pn-E4n≤0.01m n ≥1-Dw,7=1-0.1875n=1-1875, (0.01n)2 (0.01n)2 n 因此,要P40.74≤么≤0,76≥09,就要有1-1875≥09,即n≥1875 1-0.9 =18750。 n 可见,用切比雪夫不等式估计,需做18750次重复试验,才能保证A出现的频率在 0.74~0.76之间的概率至少为0.90。 (2)用德莫哇佛-一拉普拉斯极限定理估计。 4m~b(,p),其中p=0.75,由德莫哇佛-拉普拉斯极限定理可知,这时近似有 102
102 似有 ~ N(np , npq) ,其中 np = 200 0.6 = 120, npq = 120 0.4 = 48 。 设 b 是供给电力的千瓦数,要不影响生产,开工车床数必须小于 b ,这件事的概率为 P{0 b}≈ ) 48 0 120 ) ( 48 120 ( − − − b ≈ ) ( 17.32) 48 120 ( − − − b ≈ ) 48 120 ( − b ) 48 120 0 ( − − = b , 由题意可知,要有 P{0 b}≈ ) 48 120 ( − b = 0.999, 查表可得 48 b −120 = 3.0902 ,所以 b =120 + 3.0902 48 =141.4095 。 取 b =142 ,即供电 142 千瓦,就能以 99.9%的概率保证这个车间不会因供电不足而影 响生产。换句话说,每天 8 小时的工作时间中最多只有 0.1%的时间,即 0.48 分钟会受到 影响。 例 4 设在独立重复试验序列中,每次试验时事件 A 发生的概率为 0.75 ,分别用 切比雪夫不等式和德莫哇佛--拉普拉斯极限定理估计试验次数 n 需多大,才能使事件 A 发 生的频率落在 0.74 ~0.76 之间的概率至少为 0.90 。 解 设 n 为在 n 次独立重复试验中事件 A 发生的次数, n n 就是 A 发生的频率。 (1)用切比雪夫不等式估计。 由于 n ~b(n, p) , p = 0.75 ,因此 E n = np = 0.75n ,D n = npq = 0.1875n , 由切比雪夫不等式可得 {0.74 0.76} n P n = P{ 0.75n 0.01n} n − = P{ E 0.01n} n − n 2 (0.01 ) 1 n D n − 2 (0.01 ) 0.1875 1 n n = − n 1875 = 1− , 因此,要 {0.74 0.76} n P n 0.9 ,就要有 0.9 1875 1− n ,即 18750 1 0.9 1875 = − n 。 可见,用切比雪夫不等式估计,需做 18750 次重复试验,才能保证 A 出现的频率在 0.74 ~ 0.76 之间的概率至少为 0.90 。 (2)用德莫哇佛--拉普拉斯极限定理估计。 n ~b(n, p) ,其中 p = 0.75 ,由德莫哇佛--拉普拉斯极限定理可知,这时近似有