
抽象代数1 YUNCHENG UNIVERSITY 运城学院
抽 象 代 数1 运 城 学 院

1.1集合 教学目的: 1.复习集合,子集,集合相等等概念 2.复习集合关系及运算的定义和性质 3.理解阶、差集、幂集的定义
1.1 集合 教学目的: 1. 复习集合,子集,集合相等等概念 2. 复习集合关系及运算的定义和性质 3. 理解阶、差集、幂集的定义
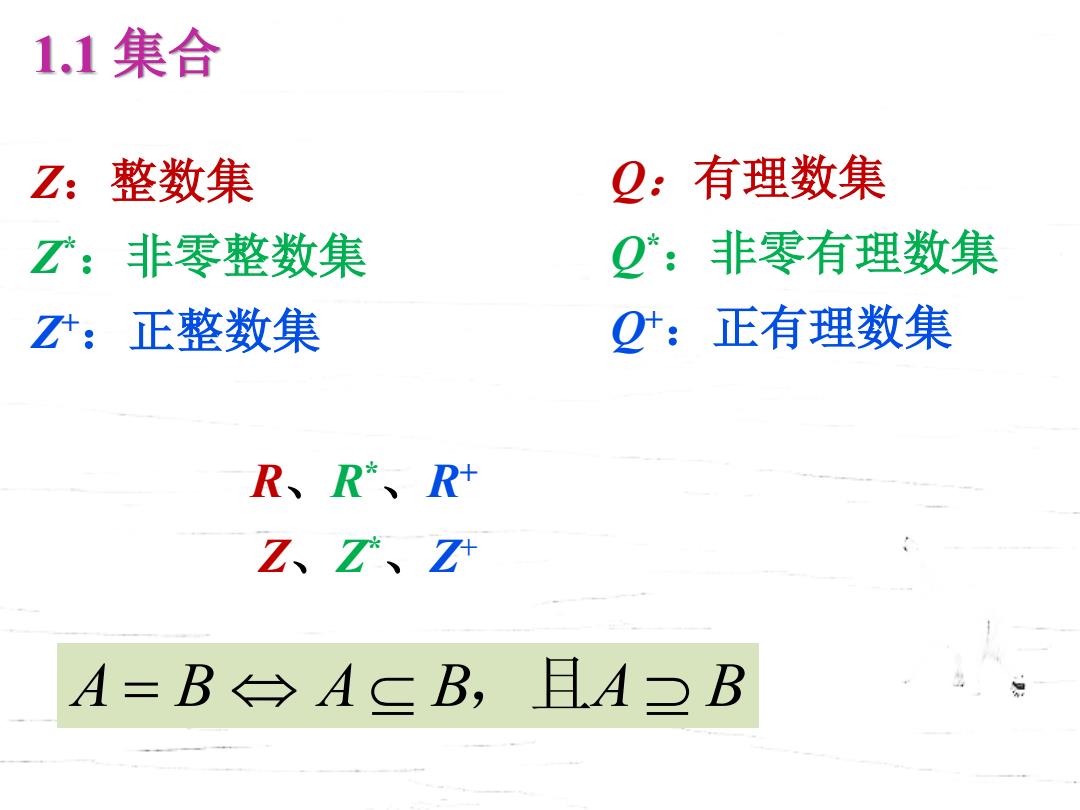
1.1集合 Z:整数集 Q:有理数集 Z:非零整数集 Q:非零有理数集 Z:正整数集 Q:正有理数集 R、R*、R Z、Zr、Z A=B→AcB,且ADB
1.1 集合 Z:整数集 Z* :非零整数集 Z+:正整数集 R、R* 、R+ Z、Z* 、Z+ Q:有理数集 Q* :非零有理数集 Q+:正有理数集 A B A B A B = ,且

1.1集合 如果集合A含有无穷多个元素,则记为A0; 如果A含有n个元素,则记为A=n。 称A为集合A的阶, 即为集合A中元素的个数。 称集合A-B={aa∈A,且a走B} 为集合A与B的差集 易知有A-B=A∩B
1.1 集合 如果集合A含有无穷多个元素,则记为 ; 如果A含有n个元素,则记为 。 称 为集合A的阶,即为集合A中元素的个数。 A = A n= A 称集合 为集合A与B的差集 易知有 A B a a A a B − = { } ,且 A B A B − =

1.1集合 集合A有很多子集,将A的所有子集放在一起 (包括空集①)也组成一个集合,称为A的幂集, 记作P(A)。 当A=n时,有P(A)=2
1.1 集合 集合A有很多子集,将A的所有子集放在一起 (包括空集 )也组成一个集合,称为A的幂集, 记作P(A)。 当 时,有 A n= ( ) =2n P A

1.2映射与变换 教学目的: 1.理解映射,单射,满射,双射,逆映射、变 换、置换、映射乘法的定义及例子 2.理解映射的象及逆象的定义 3.了解置换的多种写法
1.2 映射与变换 教学目的: 1. 理解映射,单射,满射,双射,逆映射、变 换、置换、映射乘法的定义及例子 2. 理解映射的象及逆象的定义 3. 了解置换的多种写法

1.2映射与变换 设A、B是两个集合,如果有一个法则φp,它对于 A中每个元素x,在B中都有唯一确定的元素y与 它对应,则称0为从A到B的映射。这种关系常表 示为 p:A→B 或p:x→y或y=φ(x) x→y 且称y为x在p之下的像,称x为y在p之下的原像 或逆像
1.2 映射与变换 设A、B是两个集合,如果有一个法则φ,它对于 A中每个元素x,在B中都有唯一确定的元素y与 它对应,则称φ为从A到B的映射。这种关系常表 示为 或 φ: x→y 或 y=φ(x) 且称y为x在φ之下的像,称x为y在φ之下的原像 或逆像。 : A B x y → →

1.2映射与变换 由定义可知,映射必须满足三个条件: 1)A中每个元素都有像 2)A中元素的像是唯一的 3)A中元素的像在B里
1.2 映射与变换 由定义可知,映射必须满足三个条件: 1) A中每个元素都有像 2) A中元素的像是唯一的 3) A中元素的像在B里
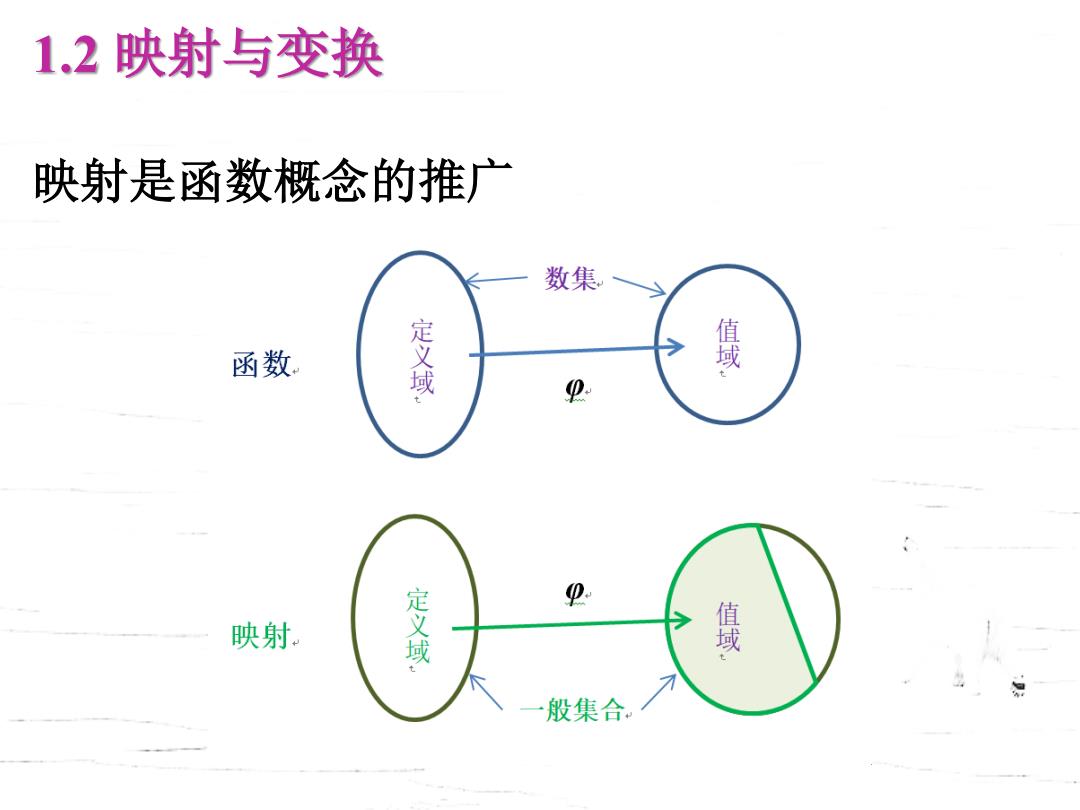
1.2映射与变换 映射是函数概念的推广 数集 函数。 定义域 傷 2 映射。 定义域 0 壤 般集合
1.2 映射与变换 映射是函数概念的推广

1.2映射与变换 设0为A到B的一个映射, 如果B中每个元素在A中都有逆像,则称0为A到 B的一个满射。 如果A中不同的元素在B中的像也不同,则称φ是 从A到B的一个单射。 如果φ既是满射又是单射,则称φ是从A到B的 个双射,或一一映射
1.2 映射与变换 设φ为A到B的一个映射, 如果B中每个元素在A中都有逆像,则称φ为A到 B的一个满射。 如果A中不同的元素在B中的像也不同,则称φ是 从A到B的一个单射。 如果φ既是满射又是单射,则称φ是从A到B的一 个双射,或一一映射