第24卷第6期 大学数学 Vol.24.No.6 2008年12月 COLLEGE MATHEMATICS Dec.2008 水塔水流量问题的广义线性回归解法 陆元鸿 (华东理工大学数学系,上海200237) [摘要]对估计水塔的水流量问题,给出一种直接对水位进行估计的广义线性回归解法,克服了由于加 水过程带来的水位数据跳跃式变化的困难,同时又避免了由水位数据估计水流量产生的误差, [关键词]水流量;广义线性回归 [中图分类号]029:0212[文献标识码]B[文章编号]1672-1454(2008)06-0124-06 1引 言 1991年国际数模竞赛(MCM1991)A题提出了一个估计水塔水流量的问题: 某个小镇上有一个高40英尺、底面直径57英尺的圆柱形水塔,每天向小镇上的居民供应生活用 水,每隔一段时间测量一次水塔中的水位,测得数据见表1(精度在0.5%以内,其中有两次水泵开动向 水塔中加水的过程,在加水过程中,没有水位记录): 表1 编号 时刻(秒) 水位(0.01英尺) 编号 时刻(秒) 水位(0.01英尺) 1 0 3175 15 46636 3350 2 3316 3110 16 49953 3260 3 6635 3054 17 53936 3167 4 10619 2994 18 57254 3087 5 13937 2947 19 60574 3012 6 17921 2892 20 64554 2927 > 21240 2850 21 68535 2842 8 25223 2795 22 71854 2767 9 28543 2752 23 75021 2697 10 32284 2697 24 79254 水泵开动 11 35932 水泵开动 25 82649 水泵开动 12 39332 水泵开动 26 85968 3475 13 39435 3550 27 89953 3397 14 43318 3445 28 93270 3340 要求估计所有时刻(包括水泵开动期间)流出水塔的水流量∫()的变化情况,并估计一天的总用 水量. 这个问题的最困难之处,是有两次水泵开动加水的过程.由于插人了两次加水过程,水位出现了未 知的跳跃式的变化,要想用常规的回归分析方法或插值方法对水位进行估计,似乎是不可能的.因此,在 这一年竞赛中获得特等奖的3个美国参赛队(Hiram College队,Ripon College队,University of Alaska-Fairbanks队),无一例外地采用了这样的做法:先设法用水位数据估计出水流量的数据(从水塔 流出的水流量是连续变化的,没有跳跃),再从水流量数据出发,用回归分析方法或插值方法估计水流量 [收稿日期]2006-08-16

第6期 陆元鸿:水塔水流量问题的广义线性回归解法 125 ()的变化,他们的做法,虽然也能得到问题的解,但是,由于他们的水流量数据是估计出来的,比起原 始数据来,显然多了一重误差,在此基础上再进行回归或插值,结果必然误差很大,所以,这样做,显然不 是一种很理想的方法, 本文给出了一种直接对水位进行估计的广义线性回归解法,克服了由于加水过程使水位数据跳跃 式变化的困难,同时又避免了从水位数据出发对水流量数据进行估计带来的误差。 2 模型的建立 为了简化问题,我们先不考虑加水过程,假定自始至终水塔中只有水流出,没有水加入, 设在时刻,水塔中水位为 H=H(t), 水塔中的总水量为 H(). 其中,D=47英尺,是水塔的底面直径 在时刻,流出水塔的水流量 f(t)=- 4H门= drD H() 反过来,则有 H(t)=H。- 4 D。 f(t)dt. 其中H。=H(0)是t=0时的水位 由于小镇上每天的用水情况周而复始,每天几乎都是相同的,所以可以认为流量f(t)是以一天时 间T=86400秒为周期的周期函数.我们知道,任何以T为周期的周期函数,都可以展开为下列形式的 Fourier级数: f(t)=a+a1cos )+6sin(学)+aeos()+sin()十. 作为近似,我们取级数前面的这5项(如果希望得到更精确的结果,还可以取更多的项).对它积分 后可得 H()=H。- =[fod 4 &[ata,eo()+sin()十a:os()+6sin(受)] 4 =A++asin(受)十Aeos(受)十asin()十Aeos()+e。 其中A,BA,A,B,g是常数,e是随机误差。 在这个方程中,函数关系显然是非线性的,但是,通过适当的变量代换,可以将它化为线性.这种可 以化为线性的非线性回归方程,称为广义线性回归方程 令x1=t,x: n(受)=o(受)=n(受)=c0(赞上式化为 H=B+Bx1十Ax2十Ax3十Ax4+Bxs+e 我们就得到了一个多元线性回归方程 用多元线性回归方法,从水位日和时间t的观测数据出发,可以直接求出它的解。 以上是在不考虑加水过程的情况下得到的结果.下面我们进一步把加水过程考虑进去, 设加水速度是均匀的,在第一次加水和第二次加水的过程中,由于加水使得水位上升的速度分别是 两个未知常数B和B. 第一次加水,相当于在水位函数式中加上一项A4(t),其中

126 大学数学 第24卷 0, 132284, u(t)= 1-32284, 32284≤185968. 把两次加水过程考虑进去,回归方程成为 H=B+8+Br:+Br3+Bx+8xs+u(t)+Bv(t)+e. 令x6=u(t),x,=o(t),上式就化为线性回归方程 H=A+月x1+Ax2+Ax3+Ax4十Ax十Ax6+Bx,十e 利用回归分析数学计算软件,可以求得未知参数B,A,A,月,B,A,R,B的估计A,B,A,A,月, B,B,,得到水位H的表达式 H=A+Ax1+月x2+月x1十Bx+Bxs+B6x6+Bx =a+a+an(受)十aco(件))+am(赞)+acos)+au(0+a0。 上述表达式中的水位H的变化,实际上包括两部分:一部分是由于小镇用水引起的水位的下降,一 部分是由于水泵加水引起的水位的上升, 从表达式中去掉代表加水过程的两项:Bu(t)和B,o(t),就得到了在不考虑加水过程的情况下纯粹 因为小镇用水引起水位日随时间:变化的函数表达式 He)=A+a+Asin()+aeos(受)十asin()十acos(樱)】 再对它求导,就得到在不考虑加水过程的情况下水流量f()随时间t变化的函数式: f=-gHe [a+aos)一Am(受)+a.()-an(受] 要求出一天24小时即T=86400秒的总用水量,可以将t=0和t=T代人(去掉加水过程的)水位 H(t)的函数式,求出一天开始时的水位和一天终了时的水位 H(0)=B+80+B2sin(0)+Bscos(0)+Bsin(0)+Bcos(0) =A十B十A, H(T)=A+月T+B2sin(2π)+月cos(2r)+B,sin(2π)+Acos(2π) =A十AT+B+A, 水位之差是 H(0)-H(T)=-BT. 得到这么一个简单的结果,其实是很自然的.因为,在水位H()的函数表达式中,除了B以外,其他各 项都是以一天时间T为周期的周期项,经过一个周期T以后,这些项的值又返回到了初始状态,前后一 减,自然就消去了 然后,用下式就可以计算出一天的总用水量 CH() 3问题的求解 用数学软件对广义线性回归方程 H=A+a+民sm(受)十aeos(受)+Asin()十Aeos()十gu+B)+e
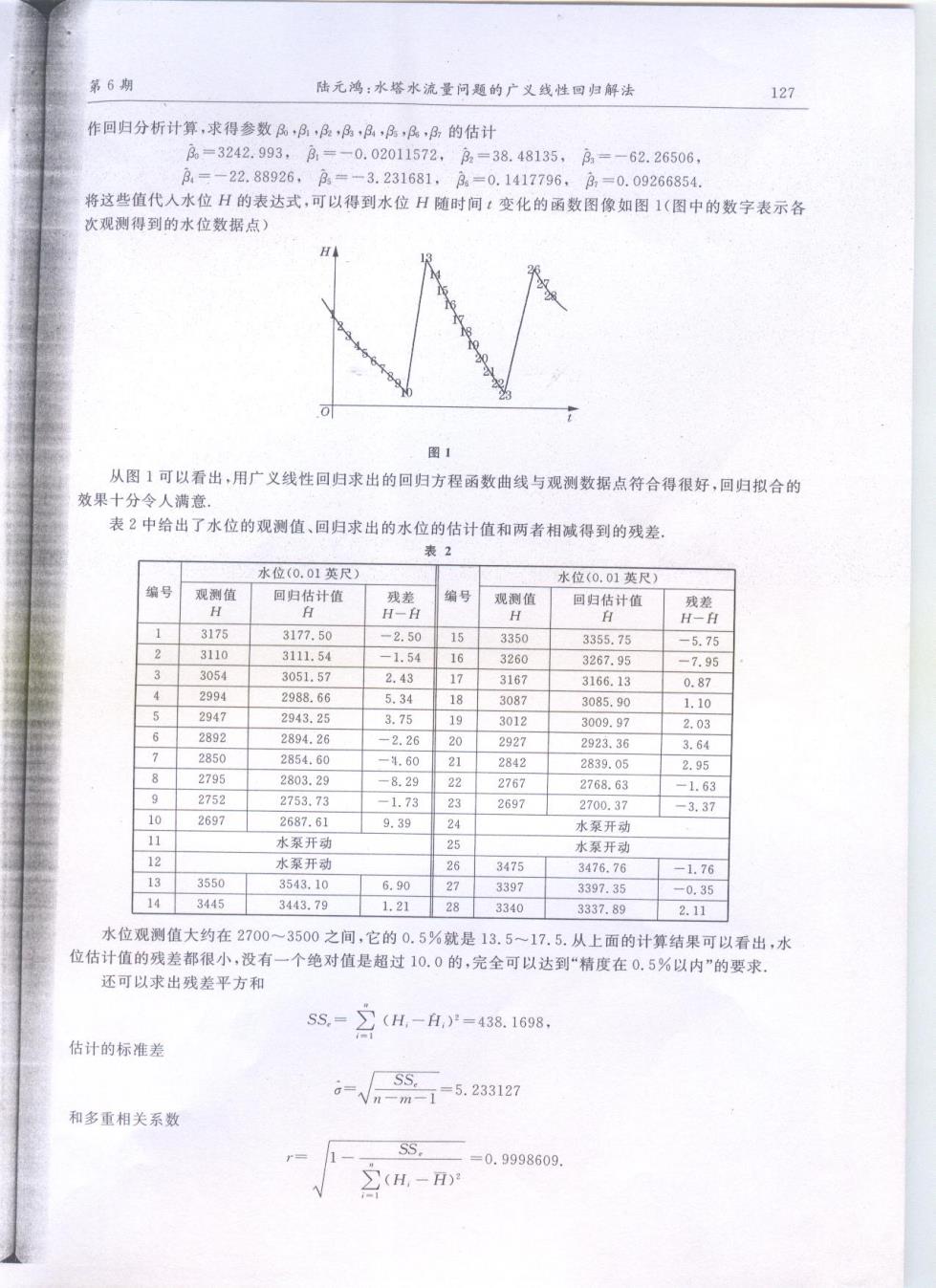
第6期 陆元鸿:水塔水流量问题的广义线性回归解法 127 作回归分析计算,求得参数R,B,A,A,A,A,A,B的估计 A=3242.993,B=-0.02011572,32=38.48135, B=-62.26506, A=-22.88926,A=-3.231681,6=0.1417796,月,=0.09266854. 将这些值代入水位H的表达式,可以得到水位H随时间t变化的函数图像如图1(图中的数字表示各 次观测得到的水位数据点) H 图1 从图1可以看出,用广义线性回归求出的回归方程函数曲线与观测数据点符合得很好,回归拟合的 效果十分令人满意。 表2中给出了水位的观测值、回归求出的水位的估计值和两者相减得到的残差 表2 水位(0.01英尺) 水位(0.01英尺)】 编号 观测值 回归估计值 残差 编号 观测值 H 9 回归估计值 残差 H-H H H H-H 3175 3177.50 -2.50 15 3350 3355.75 -5.75 2 3110 3111.54 -1.54 16 3260 3267.95 -7.95 3 3054 3051.57 2.43 17 3167 3166.13 0.87 4 2994 2988.66 5.34 18 3087 3085.90 1.10 5 2947 2943.25 3.75 19 3012 3009.97 2.03 6 2892 2894.26 -2.26 20 2927 2923.36 3.64 2850 2854.60 -4.60 2 2842 2839.05 2.95 6 2795 2803.29 -8.29 22 2767 2768.63 -1.63 9 2752 2753.73 -1.73 23 2697 2700.37 -3.37 10 2697 2687.61 9.39 24 水泵开动 11 水泵开动 25 水泵开动 12 水泵开动 26 3475 3476.76 -1.76 13 3550 3543.10 6.90 27 3397 3397.35 -0.35 14 3445 3443.79 1.21 28 3340 3337.89 2.11 水位观测值大约在2700~3500之间,它的0.5%就是13.5~17.5.从上面的计算结果可以看出,水 位估计值的残差都很小,没有一个绝对值是超过10.0的,完全可以达到“精度在0.5%以内”的要求. 还可以求出残差平方和 s5=2(H-A,=4381698. 估计的标准差 SS. =√n-m-1 =5.233127 和多重相关系数 SS. =0.9998609. 2(H-D

128 大学数学 第24卷 残差平方和、估计的标准差都很小,多重相关系数非常接近1,这些都说明我们所作的回归效果很好。 从水位H的表达式中去掉代表加水过程的两项:u(t)和B,(),就得到了在不考虑加水过程的情 况下水位H随时间:变化的函数式 H)=a+a+sim()十acos(件)+asm(赞)十acos(受) 对它求导,就得到在不考虑加水过程的情况下水流量f(:)随时间1变化的函数式 )-- 4 dt" 识[a云+ao(件))一An(受)+am(学)一a血(骨】 流量f(t)随时间t变化的函数图像如图2所示. 从图2可以看出,前面一段时间,有一个很大的低谷,这段时间, 应该是对应于夜间,在夜间,小镇上用水是很少的.以后,有一个高 峰,这应该是对应于上午,上午是一日中小镇用水的高峰.然后,在中 午,有一个小小的低谷.到了下午,又有一个高峰,但是不如上午那么 高.由此就可以知道小镇在一天中用水的变化情况.如果我们在建立 广义线性回归模型时,Fourier级数的项取得更多一些,得到的小镇上 的用水情况,还可以表现出更复杂、更精细的起伏变化 86400 同时,可以按下式计算出小镇一天的总用水量 图2 平[Ho)-HD]=-PaT=3141593X5 4 ×0.02011572×0.01×86400 =44349.5(英尺3)=331756(加仑)=1255.54(米3). 这个计算结果,与3个获得MCM1991特等奖的参赛队求出的总用水量(338000加仑,330000加仑和 326600加仑)都很接近.但是,我们求出的值,应该比他们更精确一些. 我们还可以从广义回归方程中两个加水项系数的估计值(即加水使水位上升的速度) A=0.1417796,B=0.09266854 算出两次水泵加水的加水量。 第一次水泵加水,从32284秒开始,到39435秒结束,加水量是 79A×(39435-3284)=3.141593X57×0.141796×0.01×39435-32284 D 4 =25871.4(英尺)=193531(加仑)=732.60(米1). 第二次水泵加水,从75021秒开始,到85968秒结束,加水量是 a×(85968-75021)-3.141593X57×0.0926854X0.01x(85968-75021d πD 4 =25886.1(英尺3)=193641(加仑)=733.01(米3). 我们可以看到:两次水泵加水的水量几乎相等,两次加水量的总和(387172加仑)比小镇一天的总 用水量多一些,这些,应该说都是很合理的. 最后,还要指出一点:表面上看起来,我们求出的水泵加水量,与给定的水泵加水开始时刻和结束时 刻有关.其实,由于在水泵加水过程中,没有水位的观测数据,我们的回归分析,只是对加水过程前后的 观测数据进行拟合,因此,不管加水过程内部的情况如何,回归求出的加水前后水量的变化总是一样的。 给定的水泵加水时间的长短,只会影响到估计出来的加水速度(系数A。和,)的快慢,不会影响到求出 的加水量的大小,也不会影响到其他回归系数的估计. 所以,尽管水泵加水的开始时刻和结束时刻,题目中没有明确给出,我们只能大致设定一个数值,但 是,它们设得早一些或晚一些,实际上都没有关系,最后的计算结果,仍然是一样的

129 第6期 陆元鸿:水塔水流量问题的广义线性回归解法 [参考文献] [1]Briercheck S,McCoy B and Pavalko W.A polynomial model for estimating water flow[J].The UMAP Journal, 1991,12(3):201-208. [2]Daley L.Helgemo D and Kenny J.Pump up the volume[J].The UMAP Journal,1991.12(3):209-222 [3] Baumgarter A.Rao A and Roberts E.Go with the flow[J].The UMAP Journal,1991,12(3):223-230. [4]叶其孝.数学建模教育与国际数学建模一《工科数学》专辑M们.合肥:《工科数学》杂志社,1995。 [5] 陆元鸿.数理统计方法[M门.上海:华东理工大学出版社,2005, Generalized Linear Regression Applied to the Problem on Estimating the Flow from a Water Tank LU Yuan-hong (Department of Mathematies,East China University of Science&Technology,Shanghai 200237) Abstract:To the problem on estimating water flow from a tank,generalized linear regression is applied to figure out the level in the tank directly.This approach overcomes the difficulty that the pump refills the tank-causing a sudden increase in the water level,and avoids the additional error of estimating water flow rate from water level data. Key words:water flow;generalized linear regression