
抽象代数 2.1~2.3 YUNCHENGUNIVERSITY 运城学院
抽 象 代 数 2.1~2.3 运 城 学 院

在自习室里 学弟:做我女朋友吧! 学妹:如果1×1≠1, 我就答应你。 我抄起《抽象代数》递给男孩,“你的世 界,由你来定义。 加油吧,学弟,学长只能帮你到这儿了
在自习室里 学弟:做我女朋友吧! 学妹:如果1×1≠1,我就答应你。 我抄起《抽象代数》递给男孩,“你的世 界,由你来定义。” 加油吧,学弟,学长只能帮你到这儿了

2.1群 教学内容: 1.理解群、半群、单位元、逆元的定义 2.群中单位元唯一,逆元唯一,消去律成立 3.知道一些群的例子 4.了解半群是群的条件
2.1 群 教学内容: 1. 理解群、半群、单位元、逆元的定义 2. 群中单位元唯一,逆元唯一,消去律成立 3. 知道一些群的例子 4. 了解半群是群的条件

2.1群 如果非空集合G,有代数运算。,且满足 1)结合律成立,即对任意的a,b,c∈G,有 (aob)oc=ao(boc); 2)G中有元素e,叫做G的左单位元,满足对任意 的a∈G,有ea=a; 3)对任意的a∈G,在G中有元素a1,叫做a的 左逆元,满足aloa=e; 则称G对这个代数运算作成一个群
2.1 群 如果非空集合G,有代数运算◦,且满足 1) 结合律成立,即对任意的 ,有 (a◦b)◦c=a◦(b◦c); 2) G中有元素e,叫做G的左单位元,满足对任意 的 ,有e◦a=a; 3) 对任意的 ,在G中有元素a -1,叫做a的 左逆元,满足a -1 ◦a=e; 则称G对这个代数运算作成一个群。 a b c G , , a G a G

2.1群 如果对任意的a,b∈G,有 aob=boa 则称群G为交换(Abe)群,否则群G称为非交换 群
2.1 群 如果对任意的 ,有 a◦b=b◦a 则称群G为交换(Abel)群,否则群G称为非交换 群。 a b G ,

2.1群 例1:全体非零有理数对数的普通乘法作成非零 有理数乘群。 全体正有理数对数的普通乘法作成正有理数乘群。 整数集Z对数的普通乘法不作成群 数域F上全体阶满秩方阵对矩阵的普通乘法作 成群,称为n阶线性群,记为GLnF)
2.1 群 例1:全体非零有理数对数的普通乘法作成非零 有理数乘群。 全体正有理数对数的普通乘法作成正有理数乘群。 整数集Z对数的普通乘法不作成群。 数域F上全体n阶满秩方阵对矩阵的普通乘法作 成群,称为n阶线性群,记为GLn (F)

2.1群 例2:整数集Z关于运算ab=a+b+4是一个群。 例3:正整数集Z+关于运算ab=ab不是一个群。 例4:n次单位根群: U=(cos+isin 2kπ 2kπ k=1,2,…,n-1} n n 关于数的普通乘法是群,含有n个元素
2.1 群 例2:整数集Z关于运算a◦b=a+b+4是一个群。 例3:正整数集Z+关于运算a◦b=ab不是一个群。 例4:n次单位根群: 关于数的普通乘法是群,含有n个元素。 2 2 {cos sin 1, 2, , 1} n k k U i k n n n = + = −
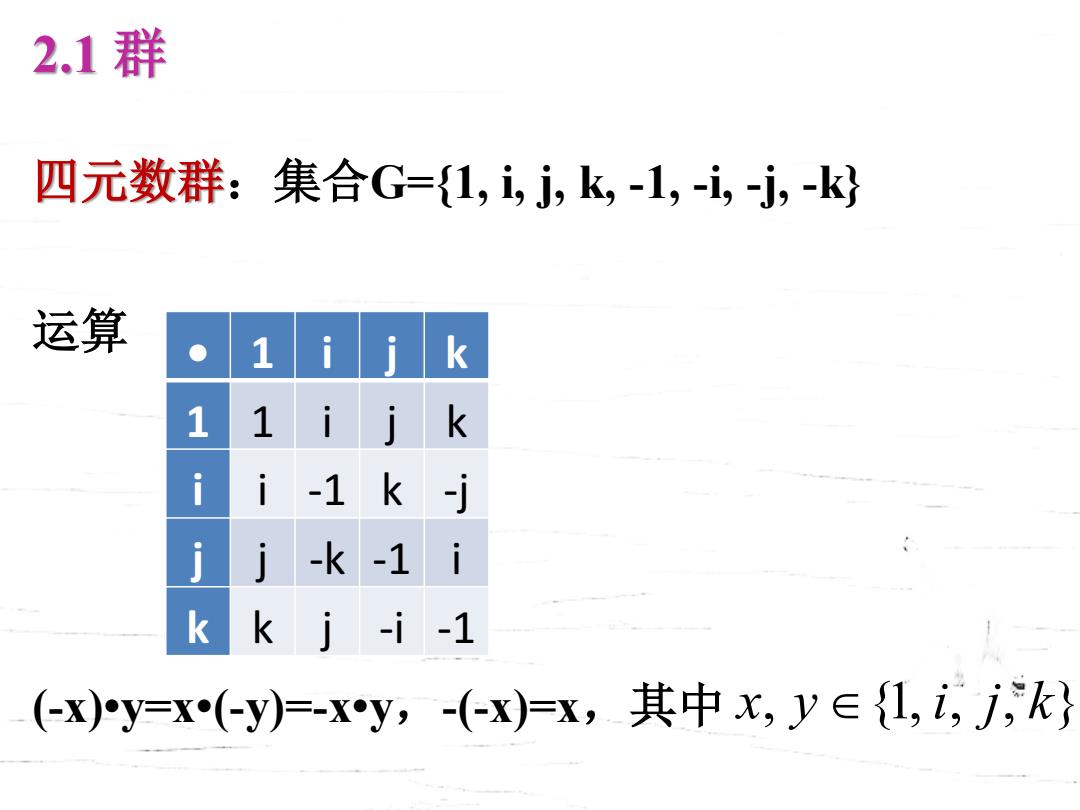
2.1群 四元数群:集合G={1,i,j,k,-1,i,j,k 运算 1 1iik i i-1 k -j j-k-1 i kk j-i-1 (x)y=x(-y)=-xy,-(-x)=x,其中x,y∈{L,i,j,k}
2.1 群 四元数群:集合G={1, i, j, k, -1, -i, -j, -k} 运算 (-x)•y=x•(-y)=-x•y,-(-x)=x,其中 • 1 i j k 1 1 i j k i i -1 k -j j j -k -1 i k k j -i -1 x y i j k , {1, , , }

2.1群 1)群定义中包含4个条件:有运算、满足结合律、 有左单位元、有左逆元。 2)群包含一个集合、一个运算,二者作为一个 整体才是群。 3)群中的运算常称为“乘法”,在不引起混淆时, ab也可记为ab
2.1 群 1) 群定义中包含4个条件:有运算、满足结合律、 有左单位元、有左逆元。 2) 群包含一个集合、一个运算,二者作为一个 整体才是群。 3) 群中的运算常称为“乘法”,在不引起混淆时, a◦b也可记为ab

2.1群 4)群中包含的元素可能有限,也可能无限,如果 一个群包含有限多个元素。就称为有限群,否则 称为无限群。 5)有限群G包含n个元素时,称n为群G的阶,并 记为G=n,无限群的阶为无限。 群G的阶即为集合G的阶
2.1 群 4) 群中包含的元素可能有限,也可能无限,如果 一个群包含有限多个元素。就称为有限群,否则 称为无限群。 5) 有限群G包含n个元素时,称n为群G的阶,并 记为 ,无限群的阶为无限。 群G的阶即为集合G的阶 G n=