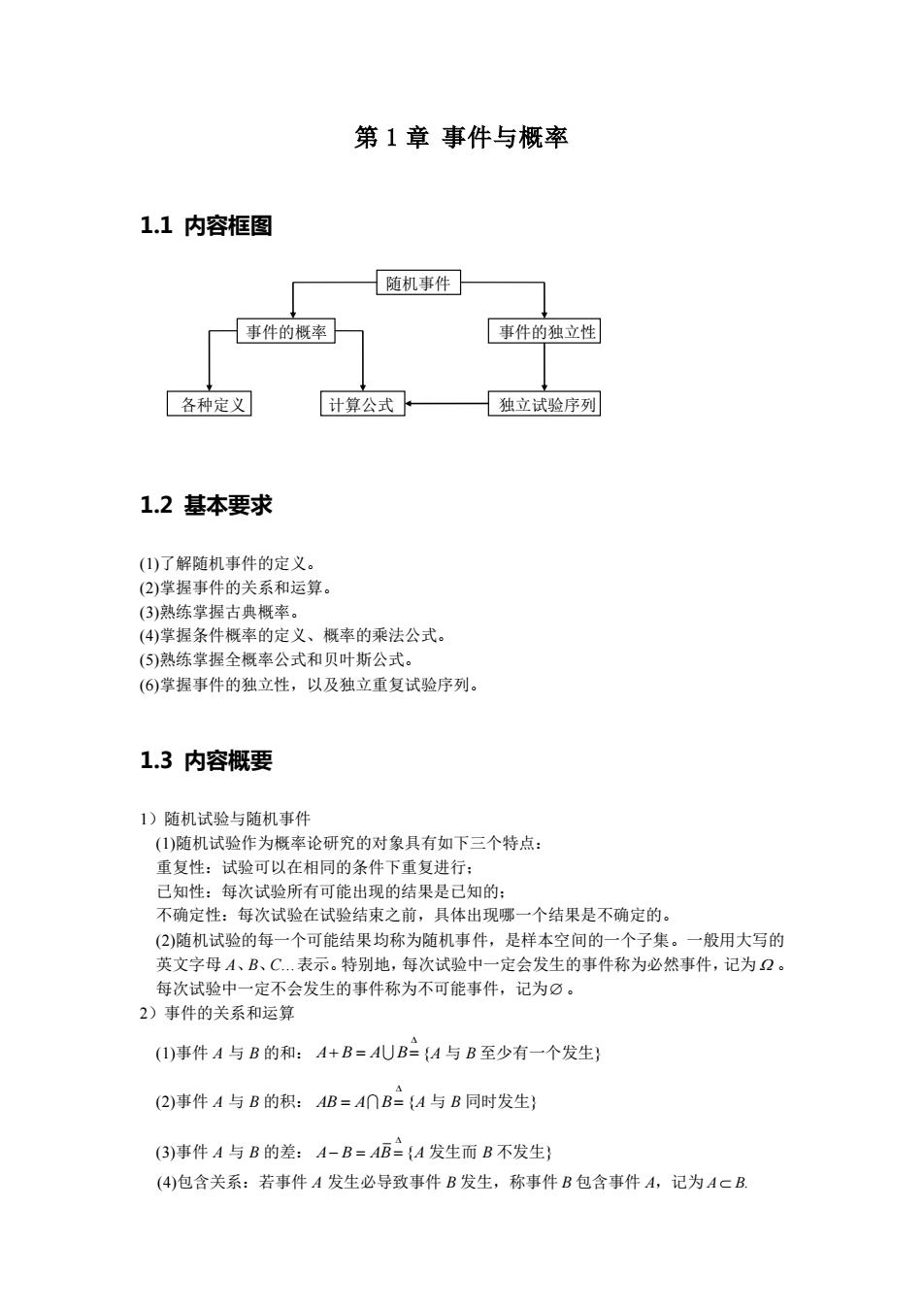
第1章事件与概率 1.1内容框图 随机事件 事件的概率 事件的独立性 各种定义 计算公式 独立试验序列 1.2基本要求 (1)了解随机事件的定义。 (2)掌握事件的关系和运算。 (3)熟练掌握古典概率。 (4)掌握条件概率的定义、概率的乘法公式。 (⑤)熟练掌握全概率公式和贝叶斯公式。 (6)掌握事件的独立性,以及独立重复试验序列。 1.3内容概要 1)随机试验与随机事件 (1)随机试验作为概率论研究的对象具有如下三个特点: 重复性:试验可以在相同的条件下重复进行: 己知性:每次试验所有可能出现的结果是己知的: 不确定性:每次试验在试验结束之前,具体出现哪一个结果是不确定的。 (2)随机试验的每一个可能结果均称为随机事件,是样本空间的一个子集。一般用大写的 英文字母A、B、C.表示。特别地,每次试验中一定会发生的事件称为必然事件,记为2。 每次试验中一定不会发生的事件称为不可能事件,记为⑦。 2)事件的关系和运算 (I)事件A与B的和:A+B=AUB={A与B至少有一个发生} (2)事件A与B的积:AB=A∩B={A与B同时发生} (3)事件A与B的差:A-B=AB={A发生而B不发生} (4)包含关系:若事件A发生必导致事件B发生,称事件B包含事件A,记为AcB
第 1 章 事件与概率 1.1 内容框图 随机事件 事件的概率 事件的独立性 各种定义 计算公式 独立试验序列 1.2 基本要求 (1)了解随机事件的定义。 (2)掌握事件的关系和运算。 (3)熟练掌握古典概率。 (4)掌握条件概率的定义、概率的乘法公式。 (5)熟练掌握全概率公式和贝叶斯公式。 (6)掌握事件的独立性,以及独立重复试验序列。 1.3 内容概要 1)随机试验与随机事件 (1)随机试验作为概率论研究的对象具有如下三个特点: 重复性:试验可以在相同的条件下重复进行; 已知性:每次试验所有可能出现的结果是已知的; 不确定性:每次试验在试验结束之前,具体出现哪一个结果是不确定的。 (2)随机试验的每一个可能结果均称为随机事件,是样本空间的一个子集。一般用大写的 英文字母 A、B、C…表示。特别地,每次试验中一定会发生的事件称为必然事件,记为 。 每次试验中一定不会发生的事件称为不可能事件,记为 。 2)事件的关系和运算 (1)事件 A 与 B 的和: A B A B + = = {A 与 B 至少有一个发生} (2)事件 A 与 B 的积: AB A B = = {A 与 B 同时发生} (3)事件 A 与 B 的差: A B AB − = = {A 发生而 B 不发生} (4)包含关系:若事件 A 发生必导致事件 B 发生,称事件 B 包含事件 A,记为 A B

(5)相等关系:若ACB且BCA,则称A与B相等,记为A=B. (⑥互不相容(互斥):若事件A与B不可能同时发生,即AB=⑦,则称A与B互不相容。 ()互相对立(互逆):若A与B同时满足:A+B=2,AB=O,则称A与B互相对立,B 为A的对立事件,记为B=A。 3)古典概率与几何概率 (1)古典概型具有两个特征: 有限性:样本点的个数为有限个: 等可能性:每个样本点发生的可能性相等。 在古典概型中,事件A的概率为 A包含的样本点数 P(A)= 样本点总数 (2)几何概型具有两个特征: ①试验的结果是无限且不可列的: ②每个结果发生的可能性是均匀的。 在几何概型中,事件A的概率为 P(A)=M. Mo 其中M与M。分别为事件A与样本空间2的几何度量。 4)概率的性质与运算公式 (1)0≤P(4)≤1,P(2)=1,P(O)=0。 (2)有限可加性:若A,A,…,An互不相容,则 (3)P(A)=1-P(4). (4)P(A-B)=P(AB)=P(A)-P(AB) 特别地,当BcA时,有P(A-B)=P(A)-P(B) (5)加法公式:对任意事件A、B、C,有 P(A+B)=P(A)+P(B)-P(AB) P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) (6条件概率:当P(B)>0时,P(4B)=P4 P(B) (7)乘法公式:对任意两个事件A、B,当P(4)>0,P(B)>0时有 P(AB)=P(A)P(BIA)=P(B)P(AB) (⑧)全概率公式:设事件组B,B,,B,互不相容,且PB)>0,事件AcB,则有 P()=P(B)P(AIB) i= (9)贝叶斯公式:设事件组B,A,B,互不相容,且P(B)>0,事件AcB,则有
2 (5)相等关系:若 A B 且 B A ,则称 A 与 B 相等,记为 A B = . (6)互不相容(互斥):若事件 A 与 B 不可能同时发生,即 AB = ,则称 A 与 B 互不相容。 (7)互相对立(互逆):若 A 与 B 同时满足: A B AB + = = , ,则称 A 与 B 互相对立,B 为 A 的对立事件,记为 B A = 。 3)古典概率与几何概率 (1)古典概型具有两个特征: 有限性:样本点的个数为有限个; 等可能性:每个样本点发生的可能性相等。 在古典概型中,事件 A 的概率为 (2)几何概型具有两个特征: ①试验的结果是无限且不可列的; ②每个结果发生的可能性是均匀的。 在几何概型中,事件 A 的概率为 ( ) = MA P A M 其中 M M A与 分别为事件 A 与样本空间 的几何度量。 4)概率的性质与运算公式 (1) 0 ( ) 1, ( ) 1, ( ) 0 = = P A P P 。 (2)有限可加性:若 1 2 , , , A A A n 互不相容,则 1 1 ( ) = = = n n i i i i P A P A (3) P A P A ( ) 1 ( ) = − 。 (4) P A B P AB P A P AB ( ) ( ) ( ) ( ) − = = − 特别地,当 B A 时,有 P A B P A P B ( ) ( ) ( ) − = − (5)加法公式: 对任意事件 A、B、C,有 P A B P A P B P AB ( ) ( ) ( ) ( ) + = + − P A B C P A P B P C P AB P BC P AC P ABC ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) + + = + + − − − + (6)条件概率:当 P B( ) 0 时, ( ) ( | ) ( ) = P AB P A B P B (7)乘法公式:对任意两个事件 A、B,当 P A P B ( ) 0, ( ) 0 时有 P AB P A P B A P B P A B ( ) ( ) ( | ) ( ) ( | ) = = (8)全概率公式:设事件组 1 2 , , , B B B n 互不相容,且 P B( ) 0 i ,事件 1 = = i n i i A B ,则有 1 ( ) ( ) ( | ) = = n i i i P A P B P A B (9)贝叶斯公式:设事件组 1 2 , , , B B B n 互不相容,且 P B( ) 0 i ,事件 1 = = i n i i A B ,则有 A包含的样本点数 样本点总数 P A( ) =

P(B)= P(B)P(AIB) (k=1,2,… P(B)P(AI B,) 5)事件的独立性 (I)定义:①对事件A与B,若P(AB)=P(A)P(B),则称A与B相互独立。 ②对n个事件A,4,…,An,如果其中任意m(2≤m≤m)个事件A,4,…,4都 有P4,A,,4)=P4)P4)…P4)则称4,4,,An相互独立。 (2)性质: ①当P(A)>0时,事件A与B相互独立一P(B)=P(B|A)。 特别地,必然事件2及不可能事件⑦与任一事件A都是相互独立的。 ②若事件A与B相互独立,则A与B,A与B,A与B也相互独立。 ③若事件A,4,,An相互独立,则其中任意m(2≤m≤)个事件仍相互独立。 6)独立试验序列(n重贝努利试验) (1)独立试验序列(n重贝努利试验)满足三个条件: ①每次试验只有两个结果:A与A: ②各次试验中,概率P(4)=pO0,则P(B1A)=0。 11.如果事件A与B相互独立,则A与B必互不相容
3 1 ( ) ( | ) ( ) ( 1,2, ) ( ) ( | ) = = = k k k n i i i P B P A B P B k P B P A B 5)事件的独立性 (1)定义:①对事件 A 与 B,若 P AB P A P B ( ) ( ) ( ) = ,则称 A 与 B 相互独立。 ②对 n 个事件 1 2 , , , A A A n ,如果其中任意 m m n (2 ) 个事件 1 2 , , , i i im A A A 都 有 1 2 1 2 ( , , , ) ( ) ( ) ( ) = i i i i i i m m P A A A P A P A P A ,则称 1 2 , , , A A A n 相互独立。 (2)性质: ①当 P A( ) 0 时,事件 A 与 B 相互独立 = P B P B A ( ) ( | ) 。 特别地,必然事件 及不可能事件 与任一事件 A 都是相互独立的。 ②若事件 A 与 B 相互独立,则 A 与 B , A 与 B , A 与 B 也相互独立。 ③若事件 1 2 , , , A A A n 相互独立,则其中任意 m m n (2 ) 个事件仍相互独立。 6)独立试验序列(n 重贝努利试验) (1)独立试验序列(n 重贝努利试验)满足三个条件: ①每次试验只有两个结果:A 与 A ; ②各次试验中,概率 P A p p ( ) (0 1) = 保持不变; ③各次试验的结果相互独立。 (2)性质:若在 n 重贝努利试验中,事件 A 发生的概率为 p p (0 1) ,则在 n 次试验中事 件 A 恰好发生 k 次的概率为 ( ) ( 0,1,2, , ; 1 ) − = = = − k k n k P k C p q k n q p n n 其中 1.4 自测题一 一、判断题(对用“+”,错用“ − ”) 1.设 A,B 是两个事件,则事件 A 与 B 都不发生可表示成 AB 。 ( ) 2.设 A,B 是两个事件,则事件 A 发生而事件 B 不发生可表示为 A AB − 。( ) 3.从编号为 1 到 10 的十张卡片中任取一张,若以 A 表示卡片编号是奇数,B 表示卡片编号 小于 5,则 A B 表示取到的卡片编号是 6,8 或 10. ( ) 4.设 A,B 是两个事件,若 B A ,则 A B = 。 ( ) 5.设 A,B 是两个事件,则 A B A B − + 。 ( ) 6.设 A,B 是两个事件,则 AB BA A B AB + = + − 。 ( ) 7. 如果事件 A 与 B 是对立事件,则 A 与 B 必互不相容。 ( ) 8.概率为零的事件必为不可能事件。 9. 设 A,B 是任意两个事件,则必有 P A B P A P B ( ) ( ) ( ) − = − 。 ( ) 10. 如果事件 A 与 B 互不相容,且 P A( ) 0 ,则 P B A ( | ) 0 = 。 ( ) 11. 如果事件 A 与 B 相互独立,则 A 与 B 必互不相容。 ( )

12.如果事件A与B互不相容,则A与B也互不相容。 13.如果事件A与B相互独立,则A与B也相互独立。 14.袋中有大小相同的2个白球和4个黑球,现随机地将球从袋中逐一摸出,则第1次摸出 白球的概率必大于第3次摸出白球的概率。 () 15.两个箱子,第一个箱子中有4个黑球,2个白球,第二个箱子中有3个黑球,3个白球。 现随机取一个箱子,再从这个箱子中取一个球,若己知取出的是白球,则此球是从第二个箱 子中取出的可能性大。 () 二、填空题: 1.从10位同学中随机抽取3人担任不同职务,问共有种取法,从10位同 学中随机派3人参加会议,共有种取法。 2.某射手向目标射击3次,记4=“第i次命中目标”(i=1,2,3),则“前两次至少有 一次未命中目标”可表示为 3.概率的统计定义为 古典概率公式P(A)= 4.袋中有4个黑球,3个白球,大小、形状相同:一次随机摸出4个球,其中恰有3个白 球的概率为。 5.从一副52张的扑克牌中,随机地抽取5张,则其中至少有一张A的概率为_ 6.设A,B都是随机事件,若BcA,且P(A)=0.8,P(B)=04,则P(B|A)= 7.将P(A),P(A+B),P(AB),P(A)+P(B)按从小到大排列成为 8.已知P(A)=0.5,P(B=0.6,P(B|A)=0.8则P(4什B)= 9.设A、B为随机事件,P()=0.7,P(A-B)=0.3,则P(A+B)=。 10.已知P(A)=0.4,P(A+B)=0.7,那么,当A、B互不相容时,P(B)=;当A、B 互相独立时,P(B)= 11.甲、乙两厂生产的电池放在一起,己知其中有75%是甲厂生产,有25%是乙厂 生产的。甲厂电池的次品率为0.02,乙厂电池的次品率为0.04。现从中任意取出 的一个电池,则它是次品的概率为 12.设盒子中有10个木质球,6个玻璃球,玻璃球有2个为红色,4个为蓝色:木 质球有3个为红色,7个为蓝色。现从盒中任取一球,用A表示“取到蓝色球”, B表示“取到玻璃球”,则P(B|A)= 13.独立掷10枚均匀硬币,恰好出现一次正面的概率为 14.甲、乙两人独立地对同一目标各射击一次,其命中率分别为0.7和0.5。现己 知目标被命中,则它是乙射中的概率为
4 12. 如果事件 A 与 B 互不相容,则 A 与 B 也互不相容。 ( ) 13. 如果事件 A 与 B 相互独立,则 A 与 B 也相互独立。 ( ) 14. 袋中有大小相同的 2 个白球和 4 个黑球,现随机地将球从袋中逐一摸出,则第 1 次摸出 白球的概率必大于第 3 次摸出白球的概率。 ( ) 15.两个箱子,第一个箱子中有 4 个黑球,2 个白球,第二个箱子中有 3 个黑球,3 个白球。 现随机取一个箱子,再从这个箱子中取一个球,若已知取出的是白球,则此球是从第二个箱 子中取出的可能性大。 ( ) 二、填空题: 1.从 10 位同学中随机抽取 3 人担任不同职务,问共有______种取法,从 10 位同 学中随机派 3 人 参加会议,共有______种取法。 2. 某射手向目标射击3次,记 Ai =“第 i 次命中目标”( i = 1,2,3),则“前两次至少有 一次未命中目标”可表示为_________。 3. 概率的统计定义为_________________, 古典概率公式 P(A)= ____________。 4. 袋中有 4 个黑球,3 个白球,大小、形状相同;一次随机摸出 4 个球,其中恰有 3 个白 球的概率为______。 5.从一副 52 张的扑克牌中,随机地抽取 5 张,则其中至少有一张 A 的概率为___. 6. 设 A,B 都是随机事件,若 B A ,且 P A( ) 0.8 = , P B( ) 0.4 = ,则 P B A ( | ) = ________。 7. 将 P A P A B P AB P A P B ( ), ( ), ( ), ( ) ( ) + + 按从小到大排列成为_________________. 8. 已知 P(A)=0.5, P(B)=0.6, P(B| A) =0.8 则 P(A+B) =________。 9.设 A、B 为随机事件, P A P A B ( ) 0.7, ( ) 0.3, = − = 则 P A B ( ) ___ + = 。 10. 已知 P(A)=0.4, P(A+B)=0.7, 那么, 当 A、B 互不相容时,P(B)= ____;当 A、B 互相独立时,P(B)= _______。 11.甲、乙两厂生产的电池放在一起,已知其中有 75%是甲厂生产,有 25%是乙厂 生产的。甲厂电池的次品率为 0.02,乙厂电池的次品率为 0.04。现从中任意取出 的一个电池,则它是次品的概率为_______。 12.设盒子中有 10 个木质球,6 个玻璃球,玻璃球有 2 个为红色,4 个为蓝色;木 质球有 3 个为红色,7 个为蓝色。现从盒中任取一球,用 A 表示“取到蓝色球”, B 表示“取到玻璃球”,则 P B A ( | ) = ________。 13. 独立掷 10 枚均匀硬币,恰好出现一次正面的概率为______。 14.甲、乙两人独立地对同一目标各射击一次,其命中率分别为 0.7 和 0.5。现已 知目标被命中,则它是乙射中的概率为________

15.如图线路中元件A、B、C能正常工作的概率均为)且各元件独立工作,则 线路能正常工作的概率为 三、选择题: 1.在含有正品和次品的甲,乙产品中各抽取一件产品检验,记事件A={抽到甲产品是正品 且乙产品是次品},则事件A的对立事件A表示()。 (A){抽到甲产品是次品且乙产品是正品}:(B){抽到甲,乙产品都是次品}: (C){抽到甲产品是次品或乙产品是正品};(D){抽到甲,乙产品都是正品} 2.打靶3发,事件4表示“击中i发”(1=01,2,3),则事件A+4,+4表示()。 (A)全部击中:(B)至少击中一发:(C)击中3发:(D)至多击中3发 3.对任意二事件A,B,与A+B=B不等价的是()。 (A)ACB; (B)BCA; (C)AB=(D)AB= 4.将6本不同的外文书,4本不同的中文书,任意放入书架,则4本中文书放在一起的概 率为()。 (A) 4171 101 (B)7: 10 (C) 4161 (D) 101 10 5.向单位圆x2+y2<1内随机地投下3点,则这3点恰有2点落在第一象限内的概率为()。 w6 (B)3 64 (c)9 (D) 64 4 6.n张奖券中有m张是有奖的,现有k个人购买,每人一张,其中至少有一个人中奖的概 率为()。 容;m总01会;0器 Ck 7.设A、B是两个事件,则下列等式中()是不正确的。 (A)当A与B独立时,P(AB)=P(A)P(B): (B)当A与B互斥时,P(AB)=P(A)P(B)方 (C)当A与B互斥时,P(AB)=0; (D)P(AB)=P(A)P(BA). 8.设P(4)=0.8,P(B)=0.7,P(AB)=0.8,则下列结论正确的是()。 (A)事件A与B互不相容: (B)ACB: (C)事件A与B互相独立: (D)P(A+B)=P(A)+P(B). 9.每次试验成功的概率为p0<p<),则在3次独立重复试验中至少失败一次的概率为 ()。 (A)1-p)3;(B)1-p3;(C)31-p);(D)1-(1-p)3
5 15.如图线路中元件 A、B、C 能正常工作的概率均为 1 2 ,且各元件独立工作,则 线路能正常工作的概率为___________. 三、选择题: 1. 在含有正品和次品的甲,乙产品中各抽取一件产品检验,记事件 A ={抽到甲产品是正品 且乙产品是次品},则事件 A 的对立事件 A 表示( )。 (A) {抽到甲产品是次品且乙产品是正品}; (B){抽到甲,乙产品都是次品}; (C) {抽到甲产品是次品或乙产品是正品}; (D){抽到甲,乙产品都是正品}. 2.打靶 3 发,事件 Ai 表示“击中 i 发”( i = 0,1,2,3 ),则事件 A A A 1 2 3 + + 表示( )。 (A)全部击中;(B)至少击中一发;(C)击中 3 发;(D)至多击中 3 发. 3.对任意二事件 AB, ,与 A B B + = 不等价的是( )。 (A) ; (B) ; (C) ; (D) . A B B A AB AB = = 4.将 6 本不同的外文书,4 本不同的中文书,任意放入书架,则 4 本中文书放在一起的概 率为( )。 (A) 4!7! 10! ; (B) 7 10 ; (C) 4!6! 10! ; (D) 4 10 . 5. 向单位圆 2 2 x y + 1 内随机地投下3点,则这3点恰有2点落在第一象限内的概率为( )。 (A) 16 1 ; (B) 64 3 ; (C) 64 9 ; (D) 4 1 . 6. n 张奖券中有 m 张是有奖的,现有 k 个人购买,每人一张,其中至少有一个人中奖的概 率为( )。 (A) 1 1 k m n m k n C C C − − ; (B) k n m C ; (C) 1 k n m k n C C − − ; (D) 1 k r m k r n C = C . 7. 设 A、B 是两个事件,则下列等式中( )是不正确的。 (A) 当 A 与 B 独立时 ,P(AB)=P(A)P(B); (B) 当 A 与 B 互斥时,P(AB)=P(A)P(B); (C) 当 A 与 B 互斥时,P(AB) =0; (D) P(AB)=P(A)P(B|A). 8. 设 P A P B P A B ( ) 0.8, ( ) 0.7, ( | ) 0.8 = = = ,则下列结论正确的是( )。 (A)事件 A 与 B 互不相容; (B) A B ; (C)事件 A 与 B 互相独立; (D) P A B P A P B ( ) ( ) ( ) + = + . 9.每次试验成功的概率为 p p (0 1) ,则在 3 次独立重复试验中至少失败一次的概率为 ( )。 (A) 3 (1 ) − p ; (B) 3 1− p ; (C) 3(1 ) − p ; (D) 3 1 (1 ) − − p . A B C

10.事件A,B同时出现的概率P(AB)=0,则()。 (A)A,B不相容: (B)AB未必是不可能事件: (C)AB是不可能事件: (D)AB独立. 1 L已知P=PB)=PCE,PAB)=PBC9=0,P(AC=G,则事件A、B、C全不 发生的概率为()。 (A) 16: (B) 4 (c) 4 (D) 6 2已知P0=P4+)=克,则PB)=( (A)1/4: (B)1/3;(C)1/2;(D)1/12 13.设A、B为任意两个事件,且ACB,P(B)>0,则下列结论中必然成立的是()。 (A)P(A)P(AB);(D)P(4A)≥P(AB) 14.飞机在雨天晚点的概率为70%,在晴天晚点的概率为20%,气象台预报明天有雨的概率 为40%,则明天飞机晚点的概率为()。 (A)0.6;(B)0.7;(C)0.4;(D)0.2. 15.每次试验的成功概率为p(0<p<1),进行重复试验,直到第10次试验才取得4次成功 的概率为()。 (A)Ciop'(1-p):(B)Cop'(1-p):(C)Cop'(1-p)s:(D)Cp'(1-p). 1.5自测题一答案 一、1.-;2.+:3+4.-:5.+:6.+:7.+:8.-;9.-;10.+;11.-:12.-;13.+;14 -:15.+。 二、1720,120:24码=A+4:3频率的稳定值,4包的拼本数:4药:5 样本点总数 -答s0341:6.05:7P4B)sP0sPA+B)sPA+PB):807:906:10.03,05 1.0.025:12. 合39:14方5 三、1.C:2.B:3.D:4.A:5.C:6.C:7.B:8.C;9.B:10.B:11.A;12.A: 13.B:14.C:15.B。 1.6典型例题 例1掷一颗骰子,观察掷出的点数。这个试验共有6个样本点,它们是: 0:表示掷出i点(i=1,2,…,6), 样本空间可以写成2={01,02,03,04,05,06}。也可以写成2={1,2,3,4,5,6},其中, 6
6 10.事件 A , B 同时出现的概率 P AB ( ) 0 = ,则 ( )。 (A) , A B 不相容; (B)AB 未必是不可能事件; (C)AB 是不可能事件; (D) , A B 独立. 11.已知 1 ( ) ( ) ( ) 4 P A P B P C = = = , P AB P BC ( ) ( ) 0 = = , 3 ( ) 16 P AC = ,则事件 A 、 B 、C 全不 发生的概率为( )。 (A) 7 16 ; (B) 3 4 ; (C) 1 4 ; (D) 9 16 . 12. 已知 1 1 ( ) , ( ) 4 2 P A P A B = + = ,则 P AB ( ) = ( )。 (A)1/4; (B)1/3; (C)1/2 ; (D)1/12. 13.设 A 、 B 为任意两个事件,且 A B , P B( ) 0 ,则下列结论中必然成立的是( )。 (A) P A P A B ( ) ( | ) ; (B) P A P A B ( ) ( | ) ; (C) P A P A B ( ) ( | ) ; (D) P A P A B ( ) ( | ) . 14.飞机在雨天晚点的概率为 70%,在晴天晚点的概率为 20%,气象台预报明天有雨的概率 为 40%,则明天飞机晚点的概率为( )。 (A)0.6; (B)0.7; (C)0.4 ; (D)0.2. 15. 每次试验的成功概率为 p p (0 1) ,进行重复试验,直到第 10 次试验才取得 4 次成功 的概率为( )。 (A) 4 4 6 10 C p p (1 ) − ;(B) 3 4 6 9 C p p (1 ) − ;(C) 4 4 5 9 C p p (1 ) − ;(D) 3 3 6 9 C p p (1 ) − . 1.5 自测题一答案 一、1. − ;2.+;3.+;4. − ;5. +;6. +;7.+;8. -;9. − ;10.+;11. − ;12. − ;13.+;14. − ;15.+。 二、1.720, 120;2. A A A A 1 2 1 2 = + ;3. 频率的稳定值, 样本点总数 A包含的样本点数 ;4. 4 35 ;5. 5 48 5 52 1 0.341 C C − ;6.0.5;7. P(AB) P(A) P(A + B) P(A) + P(B) ;8.0.7;9.0.6;10.0.3, 0.5; 11. 0.025;12. 4 11 ;13. 10 2 10 ;14. 1 17 ;15. 3 8 。 三、1.C;2. B;3. D;4. A;5.C;6. C;7.B;8. C;9. B;10. B;11. A;12. A; 13. B;14. C;15. B。 1.6 典型例题 例 1 掷一颗骰子,观察掷出的点数。这个试验共有 6 个样本点,它们是: i :表示掷出 i 点 ( i = 1 , 2 ,… ,6 ) , 样本空间可以写成 = 1 ,2 ,3 ,4 ,5 ,6 。也可以写成 = 1,2,3,4,5,6,其中

1,2,3,4,5,6分别表示出现的点数。这个随机试验的样本空间是由6个元素(6个样本 点)组成的集合。 例2抛掷两枚均匀的硬币,观察它们向上的一面是正面还是反面。对于这个试验,可 以有下列两种不同的考虑方法: (1)两枚硬币分别考虑,分别看它们是“正面向上”还是“反面向上”,这时共有4 个样本点,它们是: ⊙1:表示第一枚为正面,第二枚为正面:⊙2:表示第一枚为正面,第二枚为反面: ⊙,:表示第一枚为反面,第二枚为正面:04:表示第一枚为反面,第二枚为反面。 样本空间为2={@1,02,03,04}。 (2)两枚硬币一起考虑,看两枚硬币中总共出现几个“正面向上”,这时只有3个样本 点,它们是: 0:表示两个反面:02:表示一个正面,一个反面:0,:表示两个正面。 样本空间可以写成2={@1,02,03}。它也可以写成2={0,1,2},其中,0,1,2分别表 示出现正面的次数。 这个例子说明:样本点的选取和样本空间的构造不是唯一的,同一个试验,随着考虑角 度的不同,样本点的选取和样本空间的构造可以是不一样的。 例3在相同条件下接连不断地向同一个目标射击,直到第一次击中为止,观察直到击 中为止所需要的射击次数。因为射击次数可以是任何正整数,所以在这个试验中,样本点有 无穷多个,但是这些样本点可以排成一列,一一列举出来(可以一一列举出来的无穷多个, 称为“可列无穷多个”),即: 0:表示到击中为止需要射击i次(i=1,2,3,…), 样本空间可以表示为2={0,02,…}。它也可以表示为2={1,2,3}。其中,1,2,… 分别表示出现正面的次数。 例4在一批显像管中,任意取一只,测试它的使用寿命1。因为使用寿命1可以取 (0,+∞)中的任何一个值,所以在这个试验中,样本点有无穷多个,而且不能一一列举出来 (不能一一列举出来的无穷多个,称为“不可列无穷多个”)。这个试验的样本空间可以表示 为2={t|t>0},2中的每一点都是样本点。 例5摇奖机中有编号为0,1,2,…,9的10个奖球,随机摇出一个奖球。设事件A是 “摇出一个号码大于5的奖球”,事件B是“摇出一个号码为奇数的奖球”。 (1)写出这一试验的样本点和样本空间: (2)将下列事件表示成样本点的集合,并分别说明它们是什么事件: >
7 1,2,3,4,5,6 分别表示出现的点数。这个随机试验的样本空间是由 6 个元素(6 个样本 点)组成的集合。 例 2 抛掷两枚均匀的硬币,观察它们向上的一面是正面还是反面。对于这个试验,可 以有下列两种不同的考虑方法: (1)两枚硬币分别考虑,分别看它们是“正面向上”还是“反面向上”,这时共有 4 个样本点,它们是: 1 :表示第一枚为正面,第二枚为正面; 2 :表示第一枚为正面,第二枚为反面; 3 :表示第一枚为反面,第二枚为正面; 4 :表示第一枚为反面,第二枚为反面。 样本空间为 = 1 ,2 ,3 ,4 。 (2)两枚硬币一起考虑,看两枚硬币中总共出现几个“正面向上”,这时只有 3 个样本 点,它们是: 1 :表示两个反面; 2 :表示一个正面,一个反面; 3 :表示两个正面。 样本空间可以写成 = 1 ,2 ,3 。它也可以写成 = 0,1,2 ,其中,0,1,2 分别表 示出现正面的次数。 这个例子说明:样本点的选取和样本空间的构造不是唯一的,同一个试验,随着考虑角 度的不同,样本点的选取和样本空间的构造可以是不一样的。 例 3 在相同条件下接连不断地向同一个目标射击,直到第一次击中为止,观察直到击 中为止所需要的射击次数。因为射击次数可以是任何正整数,所以在这个试验中,样本点有 无穷多个,但是这些样本点可以排成一列,一一列举出来(可以一一列举出来的无穷多个, 称为“可列无穷多个”),即: i :表示到击中为止需要射击 i 次 ( i = 1, 2, 3, ) , 样本空间可以表示为 = 1 ,2 , 。它也可以表示为 = 1,2,3 。其中,1,2,… 分别表示出现正面的次数。 例 4 在一批显像管中,任意取一只,测试它的使用寿命 t 。因为使用寿命 t 可以取 (0,+) 中的任何一个值,所以在这个试验中,样本点有无穷多个,而且不能一一列举出来 (不能一一列举出来的无穷多个,称为“不可列无穷多个”)。这个试验的样本空间可以表示 为 = t | t 0, 中的每一点都是样本点。 例 5 摇奖机中有编号为 0,1,2, ,9 的 10 个奖球,随机摇出一个奖球。设事件 A 是 “摇出一个号码大于 5 的奖球”,事件 B 是“摇出一个号码为奇数的奖球”。 (1)写出这一试验的样本点和样本空间; (2)将下列事件表示成样本点的集合,并分别说明它们是什么事件:

A,A,B,B,A+B,AB,A-B,B-A,A+B. 解 (1)样本点共有10个,它们是: 0,:表示摇出一个号码为i的奖球,(i=0,1,…,9), 样本空间为2={00,01,…,0g}· (2) A={06,0,0g,0g}={摇出一个号码大于5的奖球}, A={00,01,02,0,04,0}={摇出一个号码不大于5的奖球), B={01,03,⊙5,01,⊙g}={摇出一个号码为奇数的奖球}, B={00,02,04,06,0g}=(摇出一个号码为偶数的奖球}, A+B={01,03,0,06,07,0g,⊙,}={摇出一个号码大于5或为奇数的奖球}, AB={01,0,}={摇出一个号码大于5而且为奇数的奖球}, A-B=AB={@6,Og}={摇出一个号码大于5而且为偶数的奖球}, B-A=BA={01,0,05}={摇出一个号码为奇数但号码不大于5的奖球), A+B=AB={0o,⊙2,04}={摇出一个号码为偶数而且号码不大于5的的奖球}。 例6设一个工人生产了4个零件。A,表示第i个零件是正品(i=1,2,3,4),试用 A,A2,A3,A4表示下列事件: (1)4个零件中没有一个是次品:(2)4个零件中至少有一个是次品: (3)4个零件中只有一个是次品;(4)4个零件中至少有三个不是次品。 解 (1)AA2A3A4:(2)AA2A3A4: (3)A444+A 444+A444+A444: (4)AAAA:+A444+A 444:+4 44 4:+4444. 例7设A,B,C是随机事件,试证(A+B)-AB=AB+AB。 证由事件差的定义、德摩根定律及分配律可知:
8 A , A , B , B , A + B , AB , A − B , B − A , A + B 。 解 (1)样本点共有 10 个,它们是: i :表示摇出一个号码为 i 的奖球,( i = 0, 1, , 9 ), 样本空间为 { , , , } = 0 1 9 。 (2) { , , , } A = 6 7 8 9 ={摇出一个号码大于 5 的奖球}, { , , , , , } A = 0 1 2 3 4 5 ={摇出一个号码不大于 5 的奖球}, { , , , , } B = 1 3 5 7 9 ={摇出一个号码为奇数的奖球}, { , , , , } B = 0 2 4 6 8 ={摇出一个号码为偶数的奖球}, { , , , , , , } A+ B = 1 3 5 6 7 8 9 ={摇出一个号码大于 5 或为奇数的奖球}, { , } AB = 7 9 ={摇出一个号码大于 5 而且为奇数的奖球}, { , } A − B = AB = 6 8 ={摇出一个号码大于 5 而且为偶数的奖球}, { , , } B − A = BA = 1 3 5 ={摇出一个号码为奇数但号码不大于 5 的奖球}, A + B { , , } = A B = 0 2 4 ={摇出一个号码为偶数而且号码不大于 5 的的奖球}。 例 6 设一个工人生产了 4 个零件。 Ai 表示第 i 个零件是正品 (i = 1,2,3,4) ,试用 1 2 3 4 A , A , A , A 表示下列事件: (1)4 个零件中没有一个是次品 ; (2)4 个零件中至少有一个是次品 ; (3)4 个零件中只有一个是次品 ; (4)4 个零件中至少有三个不是次品 。 解 (1) A1A2A3A4 ; (2) A1A2A3A4 ; (3) A1A2A3A4 + A1 A2A3A4 + A1A2 A3A4 + A1A2A3 A4 ; (4) A1A2A3A4 + A1 A2A3A4 + A1A2 A3A4 + A1A2A3 A4 + A1A2A3A4 。 例 7 设 A , B ,C 是随机事件,试证 (A+ B) − AB = AB + AB 。 证 由事件差的定义、徳摩根定律及分配律可知:
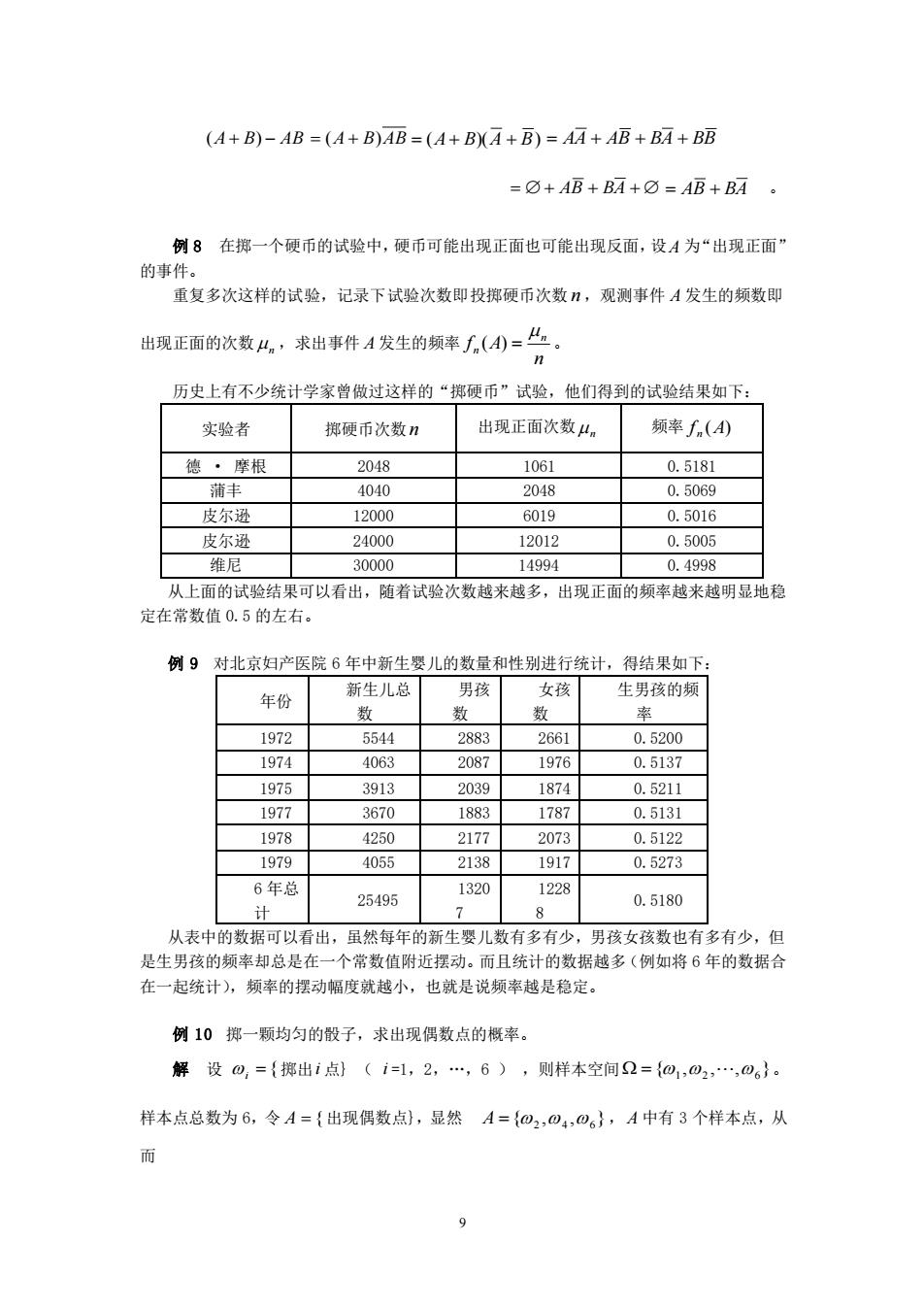
(A+B)-AB=(A+B)AB=(A+B)(A+B)=AA+AB+BA+BB =O+AB+BA+O=AB+BA。 例8在掷一个硬币的试验中,硬币可能出现正面也可能出现反面,设A为“出现正面” 的事件。 重复多次这样的试验,记录下试验次数即投掷硬币次数n,观测事件A发生的频数即 出现正面的次数4,求出事件A发生的频率f,(4)=“。 n 历史上有不少统计学家曾做过这样的“掷硬币”试验,他们得到的试验结果如下: 实验者 掷硬币次数n 出现正面次数4n 频率fn() 德·摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 皮尔逊 12000 6019 0.5016 皮尔逊 24000 12012 0.5005 维尼 30000 14994 0.4998 从上面的试验结果可以看出,随着试验次数越来越多, 出现正面的频率越来越明显地稳 定在常数值0.5的左右。 例9对北京妇产医院6年中新生婴儿的数量和性别进行统计,得结果如下: 年份 新生儿总 男孩 女孩 生男孩的频 数 数 数 率 1972 5544 2883 2661 0.5200 1974 4063 2087 1976 0.5137 1975 3913 2039 1874 0.5211 1977 3670 1883 1787 0.5131 1978 4250 2177 2073 0.5122 1979 4055 2138 1917 0.5273 6年总 1320 1228 25495 0.5180 计 7 8 从表中的数据可以看出,虽然每年的新生婴儿数有多有少,男孩女孩数也有多有少,但 是生男孩的频率却总是在一个常数值附近摆动。而且统计的数据越多(例如将6年的数据合 在一起统计),频率的摆动幅度就越小,也就是说频率越是稳定。 例10掷一颗均匀的骰子,求出现偶数点的概率。 解设@={掷出i点}(i=1,2,…,6),则样本空间2={01,⊙2,…,06}。 样本点总数为6,令A={出现偶数点),显然A={@2,⊙4,⊙6},A中有3个样本点,从 而 9
9 (A + B) − AB = (A + B)AB = (A+ B)(A + B) = AA + AB + BA + BB = + AB + BA + = AB + BA 。 例 8 在掷一个硬币的试验中,硬币可能出现正面也可能出现反面,设 A 为“出现正面” 的事件。 重复多次这样的试验,记录下试验次数即投掷硬币次数 n ,观测事件 A 发生的频数即 出现正面的次数 n ,求出事件 A 发生的频率 n f A n n ( ) = 。 历史上有不少统计学家曾做过这样的“掷硬币”试验,他们得到的试验结果如下: 实验者 掷硬币次数 n 出现正面次数 n 频率 f (A) n 德 · 摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 皮尔逊 12000 6019 0.5016 皮尔逊 24000 12012 0.5005 维尼 30000 14994 0.4998 从上面的试验结果可以看出,随着试验次数越来越多,出现正面的频率越来越明显地稳 定在常数值 0.5 的左右。 例 9 对北京妇产医院 6 年中新生婴儿的数量和性别进行统计,得结果如下: 年份 新生儿总 数 男孩 数 女孩 数 生男孩的频 率 1972 5544 2883 2661 0.5200 1974 4063 2087 1976 0.5137 1975 3913 2039 1874 0.5211 1977 3670 1883 1787 0.5131 1978 4250 2177 2073 0.5122 1979 4055 2138 1917 0.5273 6 年总 计 25495 1320 7 1228 8 0.5180 从表中的数据可以看出,虽然每年的新生婴儿数有多有少,男孩女孩数也有多有少,但 是生男孩的频率却总是在一个常数值附近摆动。而且统计的数据越多(例如将 6 年的数据合 在一起统计),频率的摆动幅度就越小,也就是说频率越是稳定。 例 10 掷一颗均匀的骰子,求出现偶数点的概率。 解 设 = { i 掷出 i 点} ( i =1,2,…,6 ) ,则样本空间 { , , , } = 1 2 6 。 样本点总数为 6,令 A = { 出现偶数点},显然 { , , } A = 2 4 6 , A 中有 3 个样本点,从 而

PA=3-1」 62 我们也可以把这个随机现象用另一个样本空间来描述,把掷骰子的结果分为两种情况: 0,表示“出现奇数点”,02表示“出现偶数点”。这时样本空间可以表示为2={0,02}。 。,所以 然奇数点和偶数点出现的可能性是相同的,从而有P(@)=P(@2)= P(4④=P(O)=2· 1 从上例可以看出,同一随机试验可用不同的样本空间加以描述,但必须注意,样本点总 数与事件A包含的样本点数的计算都要在同一样本空间中进行。 例11某种福利彩票的中奖号码由3位数字组成,每一位数字都可以是0~9中的任何 一个数字,求中奖号码的3位数字全不相同的概率。 解设事件A={中奖号码的3位数字全不相同}。 由于每一位数有10种选择,因此3位数共有103种选择,即样本点总数为103个。要3 位数各不相同,相当于要从10个数字中任选3个作无重复的排列,共有P。种选择,即A包 含的样本点数为P。个。因此, P(A)= P8_10×9×8_18 103- 100025 从这个例子可以看出,古典概型的计算往往归结为“计数”问题,经常会用到排列组合 的技巧。我们再举几个例子。 例12N个产品中,已知有M个次品,从中任取n个,求取出的n个产品中恰有m个 次品的概率。 解从N个产品中任取n个,有CW种不同取法,所以样本点总数为C”。 设A={取出的n个产品中恰有m个次品},这相当于先从M个次品中取出m个次品, 有CW种取法,再从N-M个正品中取出n-m个正品,有CM种取法,共有CWCM 种不同取法,即A中的样本点数为CWC”。 因此,取出的n个产品中恰有m个次品的概率为 P(A)= CC。 CN 0
10 2 1 6 3 P(A) = = 。 我们也可以把这个随机现象用另一个样本空间来描述,把掷骰子的结果分为两种情况: 1 表示“出现奇数点”, 2 表示“出现偶数点”。这时样本空间可以表示为 { , } = 1 2 。 显然奇数点和偶数点出现的可能性是相同的,从而有 2 1 ( ) ( ) P 1 = P 2 = ,所以 2 1 ( ) ( ) P A = P 2 = 。 # 从上例可以看出,同一随机试验可用不同的样本空间加以描述,但必须注意,样本点总 数与事件 A 包含的样本点数的计算都要在同一样本空间中进行。 例 11 某种福利彩票的中奖号码由 3 位数字组成, 每一位数字都可以是 0~9 中的任何 一个数字,求中奖号码的 3 位数字全不相同的概率。 解 设事件 A = { 中奖号码的 3 位数字全不相同 }。 由于每一位数有 10 种选择,因此 3 位数共有 3 10 种选择,即样本点总数为 3 10 个。要 3 位数各不相同,相当于要从 10 个数字中任选 3 个作无重复的排列,共有 3 P10 种选择,即 A 包 含的样本点数为 3 P10 个。因此, 3 3 10 10 ( ) P P A = 25 18 1000 10 9 8 = = 。 # 从这个例子可以看出,古典概型的计算往往归结为“计数”问题,经常会用到排列组合 的技巧。我们再举几个例子。 例 12 N 个产品中,已知有 M 个次品,从中任取 n 个,求取出的 n 个产品中恰有 m 个 次品的概率。 解 从 N 个产品中任取 n 个,有 n CN 种不同取法,所以样本点总数为 n CN 。 设 A = {取出的 n 个产品中恰有 m 个次品},这相当于先从 M 个次品中取出 m 个次品, 有 m CM 种取法,再从 N − M 个正品中取出 n −m 个正品,有 n m CN M − − 种取法,共有 m CM n m CN M − − 种不同取法,即 A 中的样本点数为 m CM n m CN M − − 。 因此,取出的 n 个产品中恰有 m 个次品的概率为 P(A) = n N n m N M m M C C C − − 。 #