
第1.5节 独立性及其应用 定义 若事件A与B满足P(AB)=P(A)PB), 则称A与B相互独立,简称A与B独立。 推论1 A.B为两个事件,若P(A)>0, 则A与B独立等价于PBA)=P(B). 若PB)>0, 则A与B独立等价于P(AB)=P(A) 推论2 在A与B,A与B,A与B,A与这四对事件中 若有一对独立,则另外三对也相互独立。 返回
返回 定义 若事件A与B满足 P(AB)=P(A)P(B), 则称A与B相互独立,简称A与B独立。 推论1 A.B为两个事件,若P(A)>0, 则A与B独立等价于P(B|A)=P(B). 若P(B)>0, 则A与B独立等价于P(A|B)=P(A). 第1.5节 独立性及其应用 推论2 在 A 与 B, 与 B,A 与 , 与 这四对事件中, 若有一对独立,则另外三对也相互独立。 A B A B

性质 若n个事件相互独立,则 P(A1A2…An)=P(A)P(A2)…P(An) P(A+A2++An)=1-P(4)P(A2)…P(An)) =1-(1-P(A)1-P(A2)…(1-P(An) 当P(A)=P(A2)=…=P(An)=p时,P(AA2…An)=p” P(A1+A2++An)=1-(1-p)". 返回
返回 性质 若n个事件相互独立,则 1 (1 ))(1 ( )) (1 ( )) ) 1 ) ( ) ( ) ) ) ( ) ( ) 1 2 1 2 1 2 1 2 1 2 n n n n n P A P A P A P A A A P A P A P A P A A A P A P A P A ( ( ( ( ( ) 1 (1 ) . ) ( ) ( ) ) 1 2 1 2 1 2 n n n n n P A A A p P A P A P A p P A A A p ( 当 ( 时, (

二项概率公式在n重贝努里试验中,如果“成功”在每 次试验中出现的概率为p,令B=在n次试验中“成功” 出现k次”,则 P(B)=Cp(1-p)”- (k=0,1,2,…,n 巴斯卡概率公式在n重贝努里试验中,如果第r次“成 功”出现在第n次试验中,则 P=C2p-(1-p)”-'p (r=1,2,…,n) 几何概率公式在n重贝努里试验中,如果第1次“成功” 出现在第n次试验中,则 P=(1-p)"-p 返回
返回 巴斯卡概率公式 在n重贝努里试验中,如果第r次“成 功” 出现在第n 次试验中,则 (1 ) ( 1,2, , ) 1 1 P C 1 p p p r n r r n r n 几何概率公式 在n重贝努里试验中,如果第1次“成功” 出现在第n 次试验中,则 P p p n 1 (1 ) 二项概率公式 在n重贝努里试验中,如果“成功”在每 次试验中出现的概率为p,令Bk=“在n 次试验中“成功” 出现k 次” ,则 P(B ) C p (1 p) (k 0,1,2, , n) k k n k k n

第2章 随机变量及分布 第2.1节 随机变量的概念 第2.2节 离散型随机变量 第2.3节 随即变量的分布 第2.4节 连续型随机变量 第2.5节 随机变量函数的分布 返回
返回 •第2.1节 随机变量的概念 •第2.3节 随即变量的分布 •第2.4节 连续型随机变量 •第2.5节 随机变量函数的分布 •第2.2节 离散型随机变量
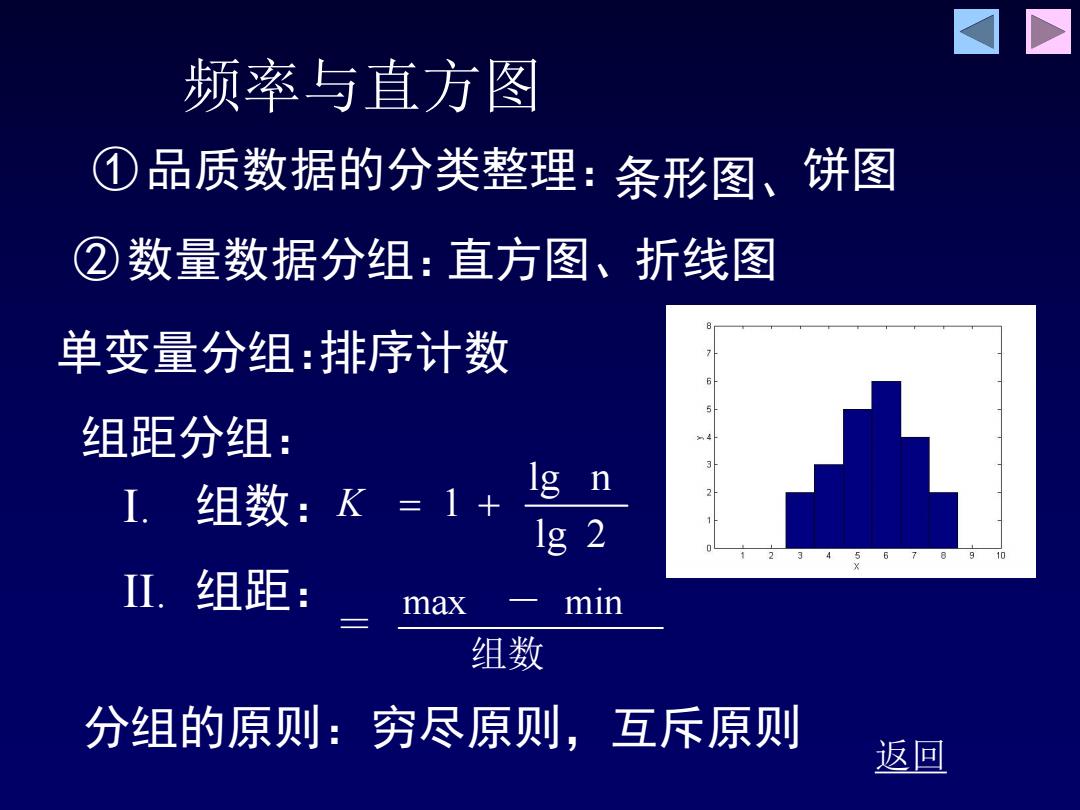
频率与直方图 ①品质数据的分类整理: 条形图、饼图 ②数量数据分组:直方图、折线图 单变量分组:排序计数 组距分组: I.组数:K=1+ lg n 1g2 10 Ⅱ.组距: max min 组数 分组的原则:穷尽原则,互斥原则 返回
返回 ①品质数据的分类整理: ②数量数据分组: 组距分组: 单变量分组: 条形图、饼图 直方图、折线图 I. 组数: II. 组距: lg 2 lg n K 1 组数 - = max min 排序计数 频率与直方图 分组的原则:穷尽原则,互斥原则

例:某商店连续40天的商品销售额(单位:万元)如下: 41 25 29 47 38 34 30 38 43 4 46 36 45 37 37 36 45 43 33 44 42 28 46 34 30 37 44 26 38 44 42 36 37 37 49 39 42 32 36 35 根据上面的数据进行适当分组,编制频数 分布表,并画出直方图。 返回
返回 例:某商店连续40天的商品销售额(单位:万元)如下: 根据上面的数据进行适当分组,编制频数 分布表,并画出直方图。 41 25 29 47 38 34 30 38 43 40 46 36 45 37 37 36 45 43 33 44 42 28 46 34 30 37 44 26 38 44 42 36 37 37 49 39 42 32 36 35
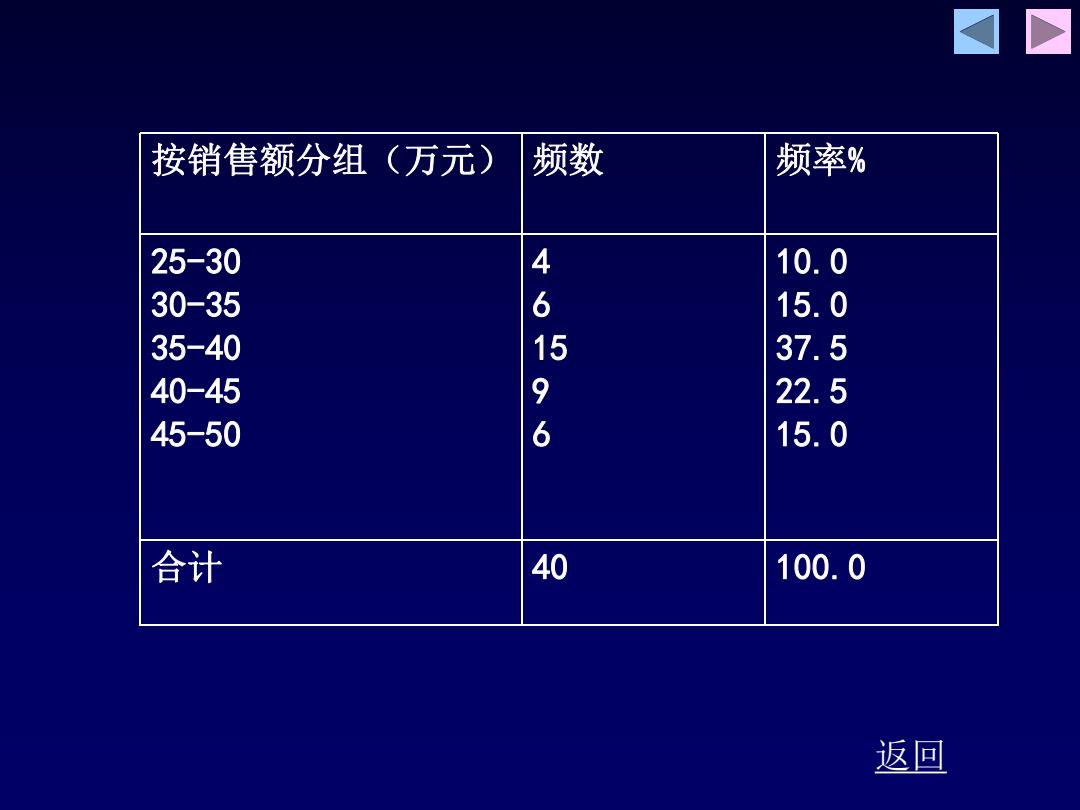
按销售额分组(万元) 频数 频率% 25-30 10.0 30-35 46 15.0 35-40 15 37.5 40-45 22.5 45-50 96 15.0 合计 40 100.0 返回
返回 按销售额分组(万元) 频数 频率% 25-30 30-35 35-40 40-45 45-50 4 6 15 9 6 10.0 15.0 37.5 22.5 15.0 合计 40 100.0
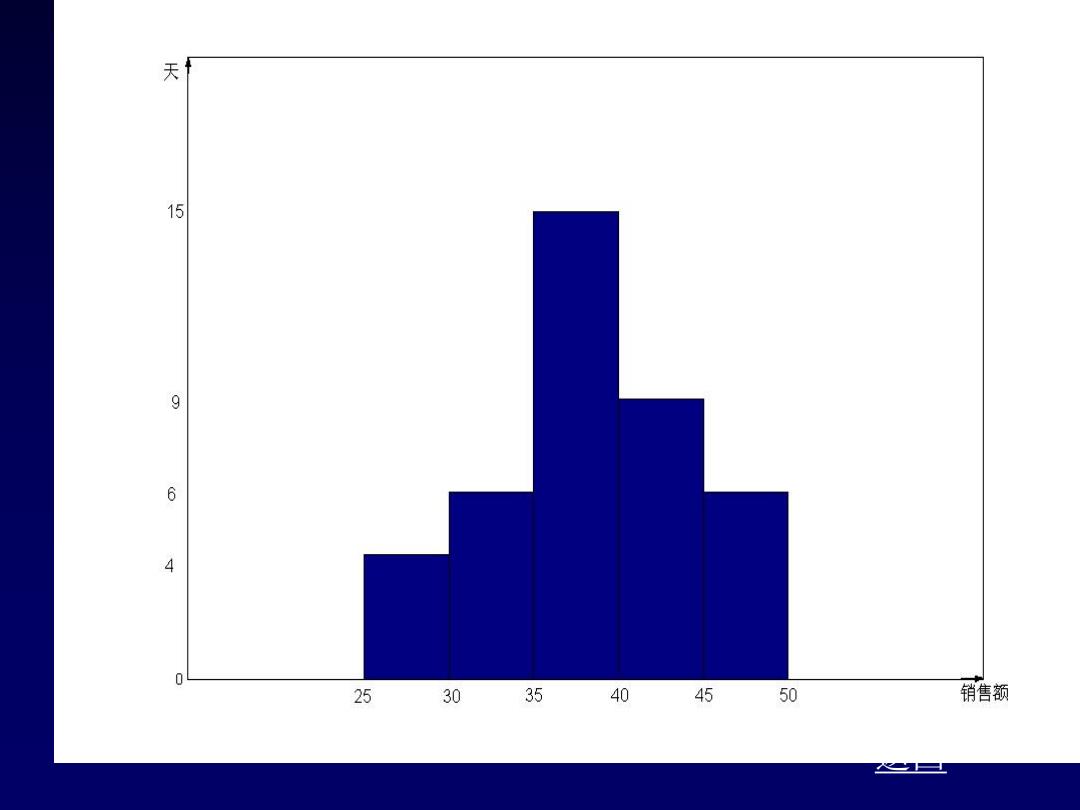
天 15 9 6 4 0 25 3035 40 45 50 销售额
返回

数据分布特征的测度 1、分布的集中趋势: (1)众数:出现频率最高的值,用M。记之。 算法(1)例1,2,4,4,5,6 则M。=4 1,2,3,3,4,5,6,6,7则M。=3orM。=6 返回
返回 数据分布特征的测度 1、分布的集中趋势: (1)众数:出现频率最高的值, 用 记之。 算法(1) 例 1,2,4,4,5,6 则 1,2,3,3,4,5,6,6,7 则 M0 M0 4 M0 3or M0 6

(2)中位数:中间位置的数, 用M。记之。 算法(1)例1,2,3,4,5,6,7则M。=4 1,2,3,4,5,6 则M。=岁=3.5 返回
返回 (2)中位数:中间位置的数, 用 记之。 算法(1) 例 1,2,3,4,5,6,7 则 1,2,3,4,5,6 则 Me Me 4 3.5 2 3 4 Me