
目录 《空间解析几何》课程教学大纲 .1 《数学分析》课程教学大纲 10 《高等代数》课程教学大纲. 29 《常微分方程》课程教学大纲 40 《复变函数》课程教学大纲 48 《近世代数》课程教学大纲 .56 《概率论》课程教学大纲 67 《实变函数》课程教学大纲 75 《数值分析》课程教学大纲. 85 《数理统计》课程教学大纲 .96 《普通物理》课程教学大纲 102 《高级语言程序设计》课程教学大纲 .108 《数学软件与数学建模》课程教学大纲 .117 《抽象代数》课程教学大纲 .121 《微分几何》课程教学大纲 125 《点集拓扑》课程教学大纲 128 《运筹学》课程教学大纲 135 《泛函分析》课程教学大纲 138 《数学物理方程》课程教学大纲 141 《群论选讲》课程教学大纲, 144 《回归分析》课程教学大纲. 147 《离散数学》课程教学大纲 150 《实分析》课程教学大纲 155 《数学史与数学文化》课程教学大纲, 159 《数学前沿简介》课程教学大纲. 162 《科技论文写作》课程教学大纲 165 《中学数学解题学》课程教学大纲 169 《初等数论》课程教学大纲 173 《初等代数研究》课程教学大纲. …177 《初等几何研究》课程教学大纲 180 《现代数学教学技术》课程教学大纲: 183 《中小学数学名师论坛》课程教学大纲! 186 《中学数学竞赛》课程教学大纲… 190 《中学数学课程标准与教材研究》课程教学大纲 .194 《中学数学教学设计》课程教学大纲」 199 《中学数学综合实践活动》课程教学大纲 206
目 录 《空间解析几何》课程教学大纲..............................................................................................................1 《数学分析》课程教学大纲....................................................................................................................10 《高等代数》课程教学大纲....................................................................................................................29 《常微分方程》课程教学大纲................................................................................................................40 《复变函数》课程教学大纲....................................................................................................................48 《近世代数》课程教学大纲....................................................................................................................56 《概率论》课程教学大纲........................................................................................................................67 《实变函数》课程教学大纲....................................................................................................................75 《数值分析》课程教学大纲....................................................................................................................85 《数理统计》课程教学大纲....................................................................................................................96 《普通物理》课程教学大纲..................................................................................................................102 《高级语言程序设计》课程教学大纲..................................................................................................108 《数学软件与数学建模》课程教学大纲..............................................................................................117 《抽象代数》课程教学大纲..................................................................................................................121 《微分几何》课程教学大纲..................................................................................................................125 《点集拓扑》课程教学大纲..................................................................................................................128 《运筹学》课程教学大纲......................................................................................................................135 《泛函分析》课程教学大纲..................................................................................................................138 《数学物理方程》课程教学大纲..........................................................................................................141 《群论选讲》课程教学大纲..................................................................................................................144 《回归分析》课程教学大纲..................................................................................................................147 《离散数学》课程教学大纲..................................................................................................................150 《实分析》课程教学大纲......................................................................................................................155 《数学史与数学文化》课程教学大纲..................................................................................................159 《数学前沿简介》课程教学大纲..........................................................................................................162 《科技论文写作》课程教学大纲..........................................................................................................165 《中学数学解题学》课程教学大纲......................................................................................................169 《初等数论》课程教学大纲..................................................................................................................173 《初等代数研究》课程教学大纲..........................................................................................................177 《初等几何研究》课程教学大纲..........................................................................................................180 《现代数学教学技术》课程教学大纲..................................................................................................183 《中小学数学名师论坛》课程教学大纲..............................................................................................186 《中学数学竞赛》课程教学大纲..........................................................................................................190 《中学数学课程标准与教材研究》课程教学大纲..............................................................................194 《中学数学教学设计》课程教学大纲..................................................................................................199 《中学数学综合实践活动》课程教学大纲..........................................................................................206
《空间解析几何》课程教学大纲 一、课程基本信息 课程 课程 5101010 空间解析几何 编号 名称 学分/学时 4学分/64学时 开课时间 第1学期 课程性质 专业基础课 先修课程 无 课程基本 考核方式 考试(平时30%、期末考试70%) 情况 课程负责人 教材: 《空间解析几何》(第四版),吕林根、许子道编,高等教育出版 社,2006年。 教材及 参考书目: 0 《空间解析几何》,黄宣国编,复旦大学出版社,2005年: 参考书 ② 《解析几何简明教程》,吴光磊,田畴编,高等教育出版社,2003 年: ③《解析几何教程》,廖华奎,王宝福编,科学出版社,2007年。 《空间解析几何》是数学与应用数学师范本科专业开设的一门重要的专业基础课, 是初等数学通向高等数学的桥梁,是用代数的方法研究几何图形的一门学科。课程讲授 向量代数的基本知识,利用代数的方法去研究空间中的曲面和曲线的位置关系,探讨柱 课程 面、锥面、旋转曲面和常见的二次曲面的几何性质。通过对本课程的学习,使学生对中 简介 学数学中的相关内容有更深刻的认识与体会,使学生学会并掌握用代数方法解决几何问 题,培养学生严密的逻辑推理能力、空间想象能力、计算能力以及解决实际问题的能 力,都有着十分重要的意义。本课程是《数学分析》和《微分几何》等后续课程的基 础。 学习目标1:掌握空间解析几何的基本概念、基本理论和求曲线与曲面方程的方法,曲 线与曲面的各种位置关系以及几种典型二次曲面的方程与几何性质。 学习目标2:培养学生严密的逻辑推理能力、空间想象能力、计算能力以及解决实际问 课程学习目标 题的能力。 学习目标3:了解空间解析几何课程的地位,为进一步学习《数学分析》和《微分几 何》等后续课程,打下坚实的基础
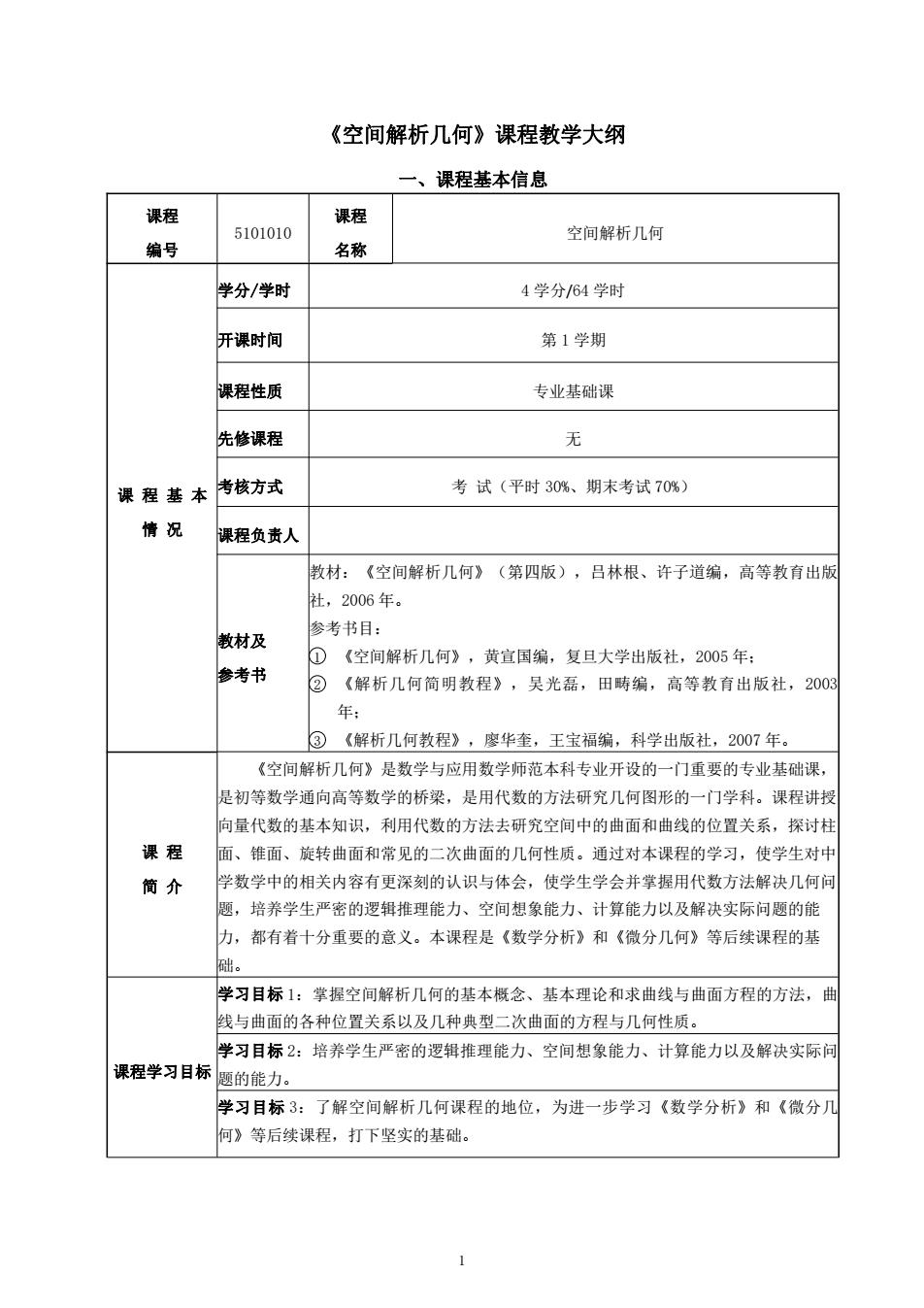
《空间解析几何》课程教学大纲 一、课程基本信息 课程 编号 5101010 课程 名称 空间解析几何 课 程 基 本 情 况 学分/学时 4 学分/64 学时 开课时间 第 1 学期 课程性质 专业基础课 先修课程 无 考核方式 考 试(平时 30%、期末考试 70%) 课程负责人 教材及 参考书 教材:《空间解析几何》(第四版),吕林根、许子道编,高等教育出版 社,2006 年。 参考书目: 1 《空间解析几何》,黄宣国编,复旦大学出版社,2005 年; 2 《解析几何简明教程》,吴光磊,田畴编,高等教育出版社,2003 年; 3 《解析几何教程》,廖华奎,王宝福编,科学出版社,2007 年。 课 程 简 介 《空间解析几何》是数学与应用数学师范本科专业开设的一门重要的专业基础课, 是初等数学通向高等数学的桥梁,是用代数的方法研究几何图形的一门学科。课程讲授 向量代数的基本知识,利用代数的方法去研究空间中的曲面和曲线的位置关系,探讨柱 面、锥面、旋转曲面和常见的二次曲面的几何性质。通过对本课程的学习,使学生对中 学数学中的相关内容有更深刻的认识与体会,使学生学会并掌握用代数方法解决几何问 题,培养学生严密的逻辑推理能力、空间想象能力、计算能力以及解决实际问题的能 力,都有着十分重要的意义。本课程是《数学分析》和《微分几何》等后续课程的基 础。 课程学习目标 学习目标 1:掌握空间解析几何的基本概念、基本理论和求曲线与曲面方程的方法,曲 线与曲面的各种位置关系以及几种典型二次曲面的方程与几何性质。 学习目标 2:培养学生严密的逻辑推理能力、空间想象能力、计算能力以及解决实际问 题的能力。 学习目标 3:了解空间解析几何课程的地位,为进一步学习《数学分析》和《微分几 何》等后续课程,打下坚实的基础。 1

二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 了解空间解析几何的发展史,以及它对几何、代数和数学 份析的发展起到的重要作用:掌握教育学、心理学和数学教育 的基本理论和基本方法:学习人类文明进步与文化发展的通识 2.3知识整合 课程学习目标1、3 知识:具有整合数学、教育学和心理学等数理知识的能力,并 会利用现代教育技术对所学的一定知识进行知识重构:熟悉中 小学数学以及教育法规的内容。 具备良好的数学素养,深入理解并掌握平面解析几何与空 间解析几何中的基本理论和方法,并能获得较强的逻辑推理能 力、空间想象能力、计算能力和解决实际问题的能力。初步掌 2.4教学能力 握数学学科的基本思想方法,具有较强的独立学习能力和创新裸程学习目标1、2、3 思维方式:了解数学教学领域的一些最新研究成果和教学方 法:懂得教育教学基本规律,掌握现代教育教学、心理学的基 本理论。 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章:向量与坐标(可支撑课程学习目标1、2) 1.教学目的和要求 理解向量及与之有关的概念,坐标系的建立。掌握向量的运算与向量乘法概念与性质,向 量共线、共面的充要条件,在直角坐标系下,用坐标进行向量的运算,数量积、向量积、混合 积和双重向量积的概念与性质。会用向量法进行有关的几何证明。 2.教学内容 第1.1节:向量的概念 第1.2节:向量的加法 第1.3节:数量乘向量 第1.4节:向量的线性关系与向量的分解 第1.5节:标架与坐标 第1.6节:向量在轴上的射影
二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 2.3 知识整合 了解空间解析几何的发展史,以及它对几何、代数和数学 分析的发展起到的重要作用;掌握教育学、心理学和数学教育 的基本理论和基本方法;学习人类文明进步与文化发展的通识 知识;具有整合数学、教育学和心理学等数理知识的能力,并 会利用现代教育技术对所学的一定知识进行知识重构;熟悉中 小学数学以及教育法规的内容。 课程学习目标 1、3 2.4 教学能力 具备良好的数学素养,深入理解并掌握平面解析几何与空 间解析几何中的基本理论和方法,并能获得较强的逻辑推理能 力、空间想象能力、计算能力和解决实际问题的能力。初步掌 握数学学科的基本思想方法,具有较强的独立学习能力和创新 思维方式;了解数学教学领域的一些最新研究成果和教学方 法;懂得教育教学基本规律,掌握现代教育教学、心理学的基 本理论。 课程学习目标 1、2、3 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章:向量与坐标(可支撑课程学习目标 1、2) 1 . 教学目的和要求 理解向量及与之有关的概念,坐标系的建立。掌握向量的运算与向量乘法概念与性质,向 量共线、共面的充要条件,在直角坐标系下,用坐标进行向量的运算,数量积、向量积、混合 积和双重向量积的概念与性质。会用向量法进行有关的几何证明。 2 . 教学内容 第 1.1 节:向量的概念 第 1.2 节:向量的加法 第 1.3 节:数量乘向量 第 1.4 节:向量的线性关系与向量的分解 第 1.5 节:标架与坐标 第 1.6 节:向量在轴上的射影 2

第1.7节:两向量的数量积 第1.8节:两向量的向量积 第1.9节:三向量的混合积 第1.10节:三向量的双重向量积 3.重点:数量积、向量积、混合积和双重向量积的概念以及其性质,向量的线性关系与向量的 分解。 4.难点:向量积、混合积和双重向量积的概念,向量共线和共面条件,用向量法进行有关的几 何证明。 5.学时:20学时 第二章轨迹与方程(可支撑课程学习目标2、3) 1.教学目的和要求 了解平面曲线、空间曲线和曲面的概念。理解曲线方程和曲面方程的各种形式的方程,球坐 标系与柱坐标系如何建立的。掌握曲线(或曲面)的参数方程与普通方程的相互转化,给出轨 迹求方程。 2.教学内容 第2.1节:平面曲线的方程 第2.2节:曲面的方程 第2.3节:空间曲线的方程 3.教学重点:曲线方程和曲面方程的各种形式的方程,曲线(或曲面)的参数方程与普通方程 的相互转化,如何根据轨迹的几何特征,写出其方程。 4.教学难点:曲线(或曲面)的参数方程与普通方程的相互转化。 5.学时:6学时 第三章平面与空间直线(可支撑课程学习目标1、2、3) 1.教学目的和要求 理解平面的法向量、离差,直线的方向向量、方向角、方向余弦和方向数,异面直线的距 离和公垂线的概念。掌握两平面相交、平行、重合的条件,直线与平面相交、平行以及直线在 平面上的条件,直线与直线异面、共面、相交、平行、垂直、重合的条件。会求平面的点法 式、截距式和一般式的方程,直线的坐标式参数、对称式和一般式的方程,以及直线的一般式 方程与对称式方程的相互转化,点到平面的距离,点与平面的离差,点到直线的距离,两平面 的夹角,直线与平面的夹角,两直线的夹角,两异面直线的距离与公垂线方程,平面束中的一 个平面的方法
第 1.7 节:两向量的数量积 第 1.8 节:两向量的向量积 第 1.9 节:三向量的混合积 第 1.10 节:三向量的双重向量积 3 . 重点:数量积、向量积、混合积和双重向量积的概念以及其性质,向量的线性关系与向量的 分解。 4 . 难点:向量积、混合积和双重向量积的概念,向量共线和共面条件,用向量法进行有关的几 何证明。 5 . 学时:20 学时 第二章 轨迹与方程(可支撑课程学习目标 2、3) 1 . 教学目的和要求 了解平面曲线、空间曲线和曲面的概念。理解曲线方程和曲面方程的各种形式的方程,球坐 标系与柱坐标系如何建立的。掌握曲线(或曲面)的参数方程与普通方程的相互转化,给出轨 迹求方程。 2 . 教学内容 第 2.1 节:平面曲线的方程 第 2.2 节:曲面的方程 第 2.3 节:空间曲线的方程 3 . 教学重点:曲线方程和曲面方程的各种形式的方程,曲线(或曲面)的参数方程与普通方程 的相互转化,如何根据轨迹的几何特征,写出其方程。 4 . 教学难点:曲线(或曲面)的参数方程与普通方程的相互转化。 5 . 学时:6 学时 第三章 平面与空间直线(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 理解平面的法向量、离差,直线的方向向量、方向角、方向余弦和方向数,异面直线的距 离和公垂线的概念。掌握两平面相交、平行、重合的条件,直线与平面相交、平行以及直线在 平面上的条件,直线与直线异面、共面、相交、平行、垂直、重合的条件。会求平面的点法 式、截距式和一般式的方程,直线的坐标式参数、对称式和一般式的方程,以及直线的一般式 方程与对称式方程的相互转化,点到平面的距离,点与平面的离差,点到直线的距离,两平面 的夹角,直线与平面的夹角,两直线的夹角,两异面直线的距离与公垂线方程,平面束中的一 个平面的方法。 3

2.教学内容 第3.1节:平面的方程 第3.2节:平面与点的相关位置 第3.3节:两平面的相关位置 第3.4节:空间直线的方程 第3.5节:直线与平面的相关位置 第3.6节:空间直线与点的相关位置 第3.7节:空间两直线的相关位置 第3.8节:平面束 3.教学重点:平面与空间直线的各种形式的方程,平面与平面、直线与直线、平面与直线、平 面与点、直线与点的相关位置。 4.教学难点:平面和空间直线的方程的建立。 5.学时:16学时 第四章柱面、锥面、旋转曲面与二次曲面(可支撑课程学习目标1、2、3) 1.教学目的和要求 理解柱面、柱面的方向、准线和母线,锥面、锥面的顶点、准线和母线,旋转曲面、旋转 曲面的旋转轴和母线的概念,椭球面、双曲面和抛物面的概念、标准方程、性质和图形。掌握 柱面、锥面和旋转曲面方程的建立以及其图形,以直线族研究单叶双曲面和双曲抛物面。 2.教学内容 第4.1节:柱面 第4.2节:锥面 第4.3节:旋转曲面 第4.4节:椭球面 第4.5节:双曲面 第4.6节:抛物面 第4.7节:单叶双曲面与双曲抛物面的直母线 3.重点:建立柱面、锥面和旋转曲面方程的方法,求解以坐标轴为轴的旋转曲面方程的方法, 二次曲面图形的特征。 4.难点:柱面、锥面、旋转曲面、椭球面、双曲面和抛物面图形的画法,直母线方程,以直线 族研究单叶双曲面和双曲抛物面。 5.学时:14学时
2 . 教学内容 第 3.1 节:平面的方程 第 3.2 节:平面与点的相关位置 第 3.3 节:两平面的相关位置 第 3.4 节:空间直线的方程 第 3.5 节:直线与平面的相关位置 第 3.6 节:空间直线与点的相关位置 第 3.7 节:空间两直线的相关位置 第 3.8 节:平面束 3 . 教学重点:平面与空间直线的各种形式的方程,平面与平面、直线与直线、平面与直线、平 面与点、直线与点的相关位置。 4 . 教学难点:平面和空间直线的方程的建立。 5 . 学时:16 学时 第四章 柱面、锥面、旋转曲面与二次曲面(可支撑课程学习目标 1、2、3) 1 .教学目的和要求 理解柱面、柱面的方向、准线和母线,锥面、锥面的顶点、准线和母线,旋转曲面、旋转 曲面的旋转轴和母线的概念,椭球面、双曲面和抛物面的概念、标准方程、性质和图形。掌握 柱面、锥面和旋转曲面方程的建立以及其图形,以直线族研究单叶双曲面和双曲抛物面。 2 .教学内容 第 4.1 节:柱面 第 4.2 节:锥面 第 4.3 节:旋转曲面 第 4.4 节:椭球面 第 4.5 节:双曲面 第 4.6 节:抛物面 第 4.7 节:单叶双曲面与双曲抛物面的直母线 3 .重点:建立柱面、锥面和旋转曲面方程的方法,求解以坐标轴为轴的旋转曲面方程的方法, 二次曲面图形的特征。 4 .难点:柱面、锥面、旋转曲面、椭球面、双曲面和抛物面图形的画法,直母线方程,以直线 族研究单叶双曲面和双曲抛物面。 5 . 学时:14 学时 4
第五章二次曲线的一般理论(可支撑课程学习目标1、3) 1.教学目的和要求 了解二次曲线按其渐近方向或中心的分类。理解二次曲线的渐近方向、中心、奇异点、正 常点、渐近线和切线的概念。会求二次曲线的渐近线、切线和直径,判断二次曲线与直线的相 关位置。 2.教学内容 第5.1节:二次曲线与直线的相关位置 第5.2节:二次曲线的渐近方向、中心、渐近线 第5.3节:二次曲线的切线 第5.4节:二次曲线的直径 3.教学重点:二次曲线的渐近方向、中心、渐近线、切线和直径,判断二次曲线与直线的相 关位置,求二次曲线的渐近线,切线和直径。 4.教学难点:求二次曲线的渐近线,切线和直径。 一.学时:8学时 (二)《空间解析几何》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标1 课程学习目标2 课程学习目标3 第1.1-1.10节 H H 第2.1-2.3节 M 第3.1-3.8节 H H 夕 第4.1-4.7节 H M H 第5.1-5.4节 H M (三)《空间解析几何》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 学习目标1:掌握空间解析几何的基本概念、 1.本课程以课堂讲授为主,结合课堂提问进行 基本理论和求曲线与曲面方程的方法,曲线与 教学,同时对适合的内容以多媒体辅助教学。 曲面的各种位置关系及几种典型二次曲面的方 注重向量代数的基本知识,空间曲线和曲面的 程与几何性质。 方程的建立以及其性质的详细讲解:注重逻辑 学习目标2:培养学生严密的逻辑推理能力、 思维能力、空间想象能力、计算能力以及解决 空间想象能力、计算能力以及解决实际问题的 实际问题的能力的培养。 能力。 5
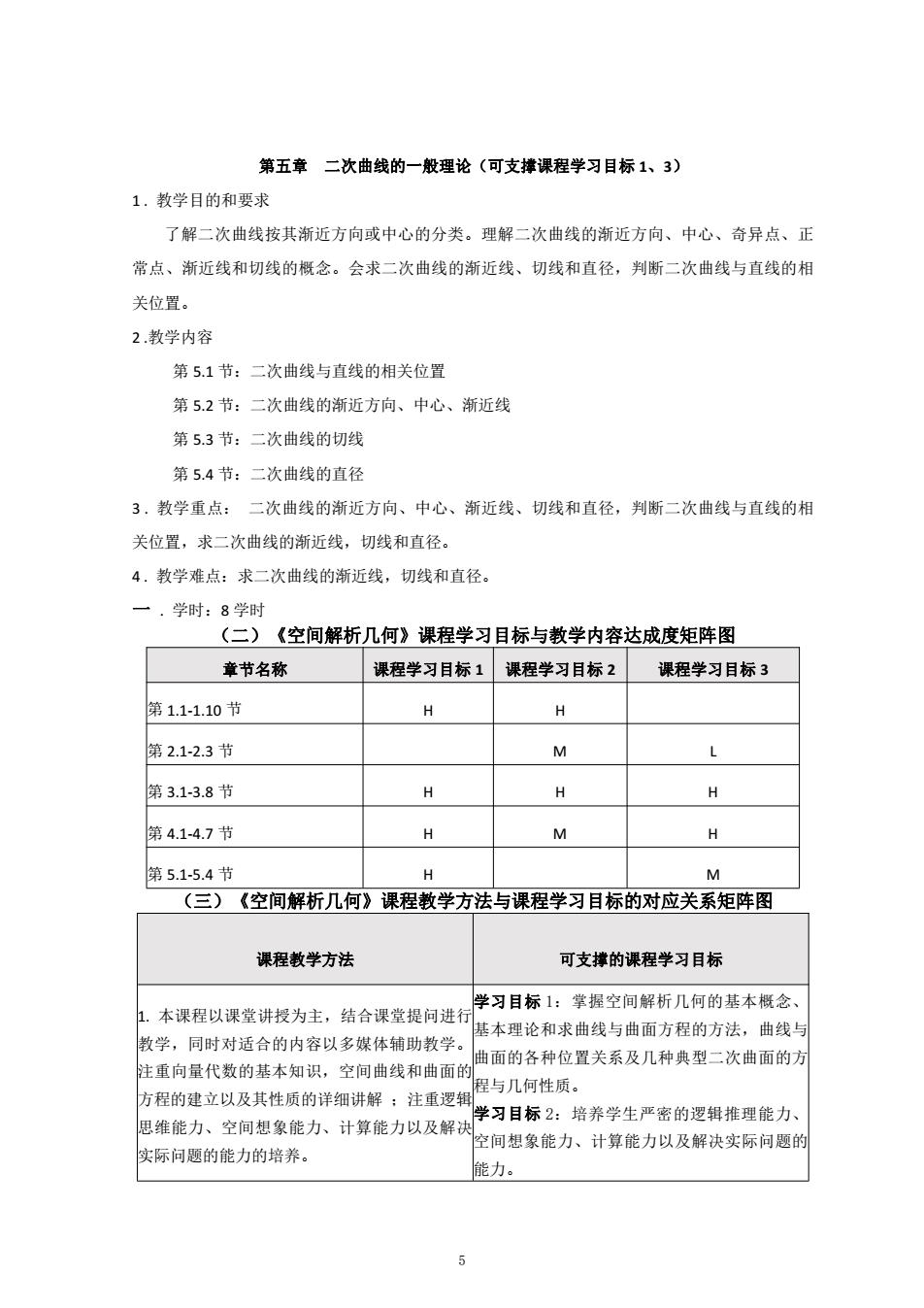
第五章 二次曲线的一般理论(可支撑课程学习目标 1、3) 1 . 教学目的和要求 了解二次曲线按其渐近方向或中心的分类。理解二次曲线的渐近方向、中心、奇异点、正 常点、渐近线和切线的概念。会求二次曲线的渐近线、切线和直径,判断二次曲线与直线的相 关位置。 2 .教学内容 第 5.1 节:二次曲线与直线的相关位置 第 5.2 节:二次曲线的渐近方向、中心、渐近线 第 5.3 节:二次曲线的切线 第 5.4 节:二次曲线的直径 3 . 教学重点: 二次曲线的渐近方向、中心、渐近线、切线和直径,判断二次曲线与直线的相 关位置,求二次曲线的渐近线,切线和直径。 4 . 教学难点:求二次曲线的渐近线,切线和直径。 一 . 学时:8 学时 (二)《空间解析几何》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标 1 课程学习目标 2 课程学习目标 3 第 1.1-1.10 节 H H 第 2.1-2.3 节 M L 第 3.1-3.8 节 H H H 第 4.1-4.7 节 H M H 第 5.1-5.4 节 H M (三)《空间解析几何》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 1. 本课程以课堂讲授为主,结合课堂提问进行 教学,同时对适合的内容以多媒体辅助教学。 注重向量代数的基本知识,空间曲线和曲面的 方程的建立以及其性质的详细讲解 ;注重逻辑 思维能力、空间想象能力、计算能力以及解决 实际问题的能力的培养。 学习目标 1:掌握空间解析几何的基本概念、 基本理论和求曲线与曲面方程的方法,曲线与 曲面的各种位置关系及几种典型二次曲面的方 程与几何性质。 学习目标 2:培养学生严密的逻辑推理能力、 空间想象能力、计算能力以及解决实际问题的 能力。 5
学习目标3:了解空间解析几何课程的地位, 为进一步学习《数学分析》和《微分几何》等 后续课程,打下坚实的基础。 2.注意运用启发式教学,对基本概念和基本理 论的学习,建立起空间观念,注意培养学生的学习目标2:培养学生严密的逻辑推理能力、 逻辑思维、空间想象能力和计算能力,培养学空间想象能力、计算能力以及解决实际问题的 生的理论联系实际问题的能力,从而培养学生能力。 学习数学的兴趣。 3.注意运用互动式教学法,从而引导学生参与 课堂,进而培养学生独立思考、参与讨论的习学习目标3:了解空间解析几何课程的地位, 惯,让学生了解空间解析几何课程的地位,讲伪进一步学习《数学分析》和《微分几何》等 授《空间解析几何》与《数学分析》和《微分后续课程,打下坚实的基础。 几何》等后续课程的联系。 (四)《空间解析几何》课程学习目标与考核内容、考核方式的关系矩阵图 课程学习目标 考核内容 考核方式 理解向量及与之有关的概念。掌握向量的运算与向 量乘法、数量积、向量积、混合积和双重向量积的概念 与性质,向量共线、共面的充要条件,在直角坐标系 下,用坐标进行向量的运算。 了解平面曲线、空间曲线和曲面的概念。掌握曲线 或曲面)的参数方程与普通方程的相互转化,给出轨迹求 方程。 理解平面的法向量,离差,直线的方向向量、方向.平时课堂表现、作业 角、方向余弦和方向数,异面直线的距离和公垂线的概完成情况 课程学习目标1 念。掌握两平面相交、平行、重合,直线与平面相交、2.期末考试 平行以及直线在平面上,直线与直线异面、共面、相 交、平行、垂直、重合的条件。会求平面(或直线)的 各种形式的方程,点与平面的离差,直线的一般方程与 对称式方程的相互转化,公垂线方程,平面束中的一个 平面。 理解柱面、柱面的方向、准线和母线,锥面、锥面 的顶点、准线和母线,旋转曲面、旋转曲面的旋转轴和 母线的概念。掌握椭球面、双曲面和抛物面的概念及其 6
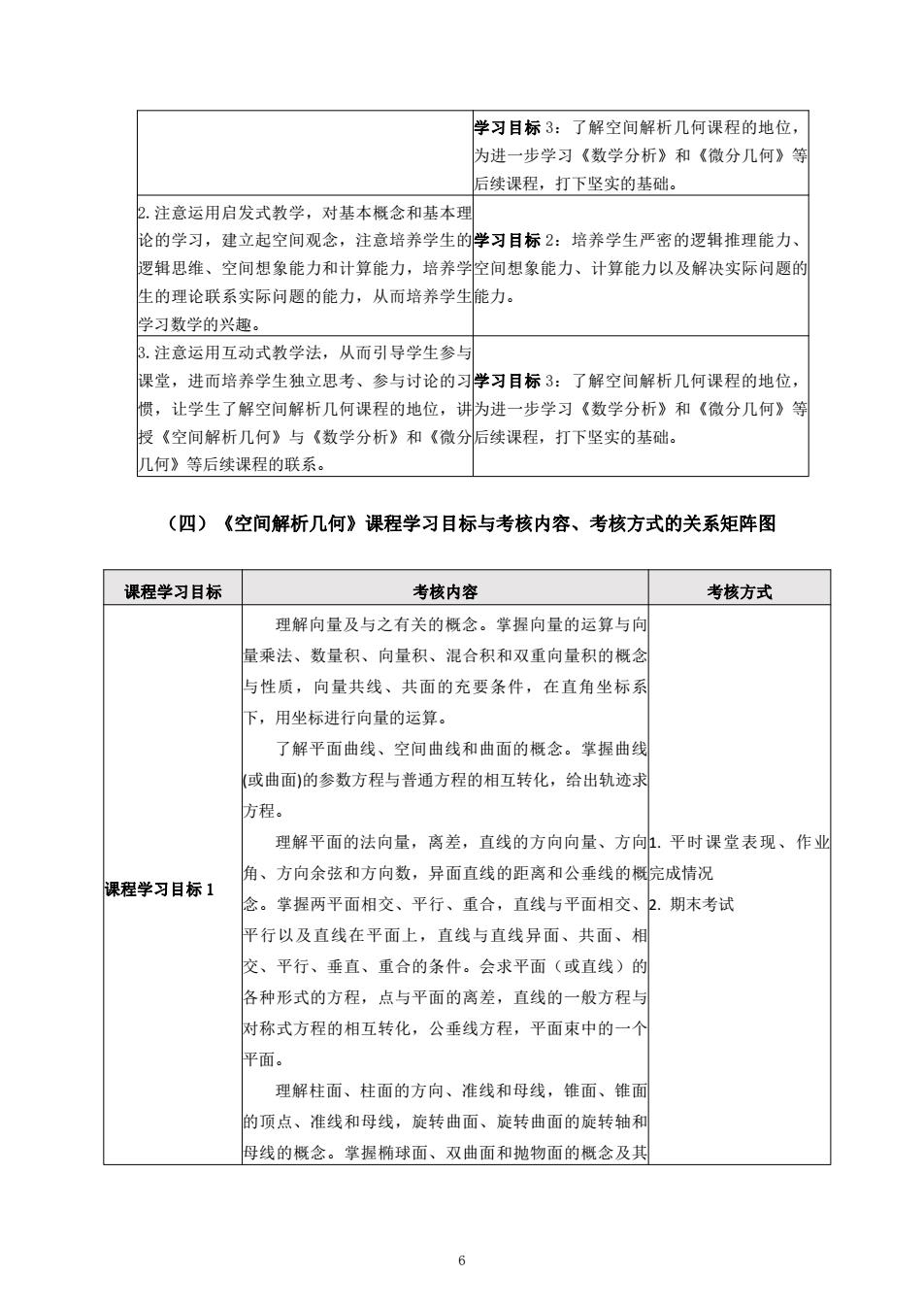
学习目标 3:了解空间解析几何课程的地位, 为进一步学习《数学分析》和《微分几何》等 后续课程,打下坚实的基础。 2.注意运用启发式教学,对基本概念和基本理 论的学习,建立起空间观念,注意培养学生的 逻辑思维、空间想象能力和计算能力,培养学 生的理论联系实际问题的能力,从而培养学生 学习数学的兴趣。 学习目标 2:培养学生严密的逻辑推理能力、 空间想象能力、计算能力以及解决实际问题的 能力。 3.注意运用互动式教学法,从而引导学生参与 课堂,进而培养学生独立思考、参与讨论的习 惯,让学生了解空间解析几何课程的地位,讲 授《空间解析几何》与《数学分析》和《微分 几何》等后续课程的联系。 学习目标 3:了解空间解析几何课程的地位, 为进一步学习《数学分析》和《微分几何》等 后续课程,打下坚实的基础。 (四)《空间解析几何》课程学习目标与考核内容、考核方式的关系矩阵图 课程学习目标 考核内容 考核方式 课程学习目标 1 理解向量及与之有关的概念。掌握向量的运算与向 量乘法、数量积、向量积、混合积和双重向量积的概念 与性质,向量共线、共面的充要条件,在直角坐标系 下,用坐标进行向量的运算。 了解平面曲线、空间曲线和曲面的概念。掌握曲线 (或曲面)的参数方程与普通方程的相互转化,给出轨迹求 方程。 理解平面的法向量,离差,直线的方向向量、方向 角、方向余弦和方向数,异面直线的距离和公垂线的概 念。掌握两平面相交、平行、重合,直线与平面相交、 平行以及直线在平面上,直线与直线异面、共面、相 交、平行、垂直、重合的条件。会求平面(或直线)的 各种形式的方程,点与平面的离差,直线的一般方程与 对称式方程的相互转化,公垂线方程,平面束中的一个 平面。 理解柱面、柱面的方向、准线和母线,锥面、锥面 的顶点、准线和母线,旋转曲面、旋转曲面的旋转轴和 母线的概念。掌握椭球面、双曲面和抛物面的概念及其 1. 平时课堂表现、作业 完成情况 2. 期末考试 6
性质,以直线族研究单叶双曲面和双曲抛物面。 了解二次曲线按其渐近方向或中心的分类。理解 次曲线的渐近方向、中心、奇异点、正常点、渐近线和 切线的概念。会求二次曲线的渐近线、切线和直径。判 断二次曲线与直线的相关位置。 用向量法求三角形和平行四边形的面积,平行六面 体的体积,以及进行有关的几何证明。 . 平时课堂表现、作业 求点到平面(直线)的距离,面与面、线与线和线 完成情况 课程学习目标2 与面的距离,直线与直线、平面与平面和直线与平面的 . 期末考试 夹角。 曲线、平面、柱面、锥面、旋转曲面、椭球面、双 曲面和抛物面的图形。 1. 平时课堂表现、作业 1. 曲线(或曲面)的一般方程与参数方程的转化: 完成情况 课程学习目标3 2. 掌握柱面、锥面和旋转曲面方程的建立: 2.期末考试 椭球面、双曲面和抛物面的标准方程。 (五)课程考核方法 1.平时课堂表现、作业完成情况(30%) 2.期末考试(闭卷,70%) (六)课程成绩评定方法及其与课程学习目标的关系 平时课堂表现、作业完成情况(30%)、期末考试(闭卷,70%) 课程学习目标 期末考试(闭卷) 课程分目标达成评价方法 成绩评定方法 课程学习目标1 约70% 课程学习目标2 约15% 分目标达成度=0.3×(平时课堂表现、作 课程学习目标3 约15% 业完成情况)+0.7×(期末考试) 合计 100 (七)课程学习目标与评分标准的对应关系 评分标准 课程学习目标 90-100 80-89 60-79 0-59 优 良 中/及格 不及格 ①能准确理解向量及与①理解向量及与之①基本理解向量及对于空间解析几何的 课程学习目标1 之有关的概念。熟练掌握有关的概念。掌握向与之有关的概念。基基本概念、基本理论
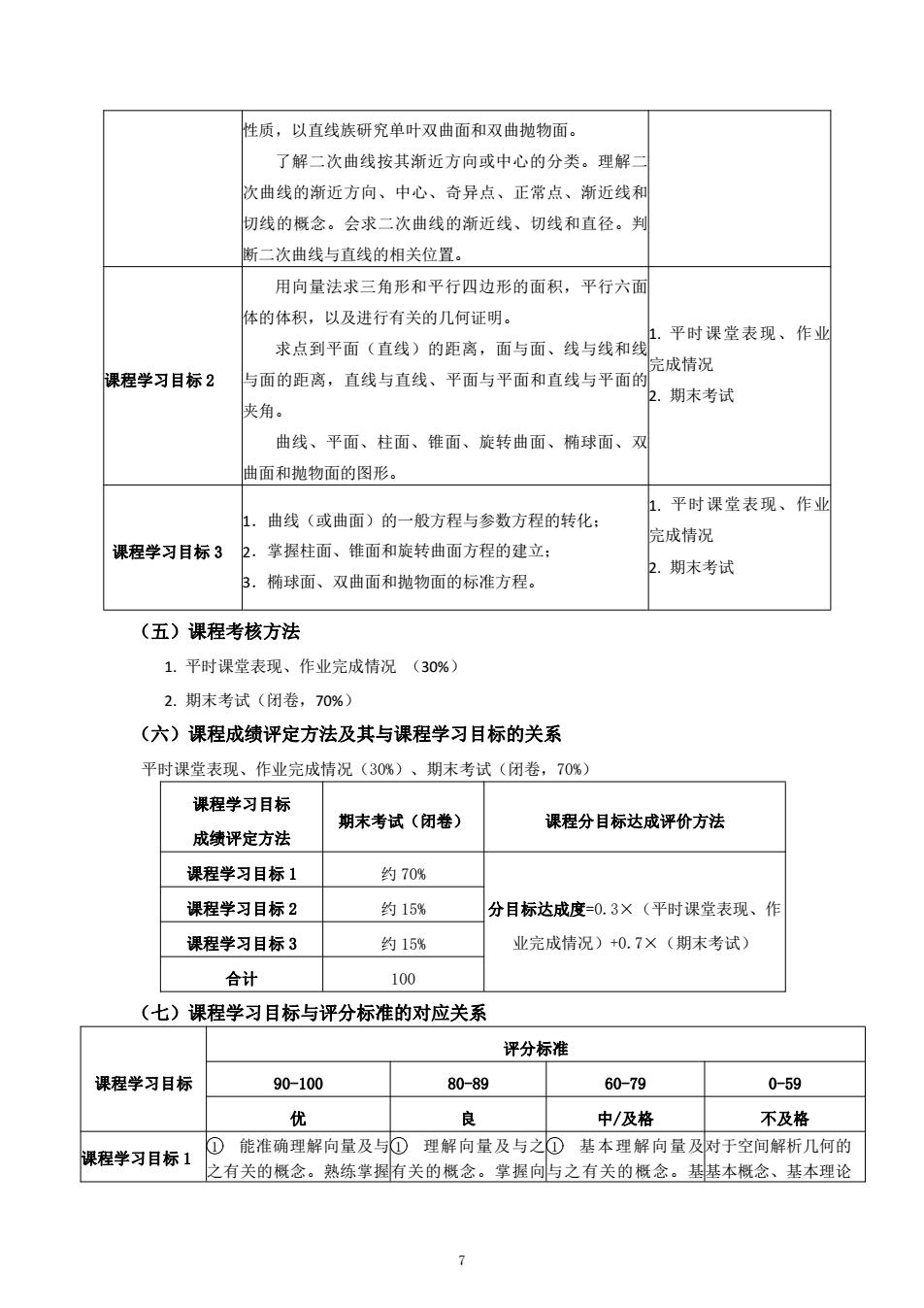
性质,以直线族研究单叶双曲面和双曲抛物面。 了解二次曲线按其渐近方向或中心的分类。理解二 次曲线的渐近方向、中心、奇异点、正常点、渐近线和 切线的概念。会求二次曲线的渐近线、切线和直径。判 断二次曲线与直线的相关位置。 课程学习目标 2 用向量法求三角形和平行四边形的面积,平行六面 体的体积,以及进行有关的几何证明。 求点到平面(直线)的距离,面与面、线与线和线 与面的距离,直线与直线、平面与平面和直线与平面的 夹角。 曲线、平面、柱面、锥面、旋转曲面、椭球面、双 曲面和抛物面的图形。 1. 平时课堂表现、作业 完成情况 2. 期末考试 课程学习目标 3 1.曲线(或曲面)的一般方程与参数方程的转化; 2.掌握柱面、锥面和旋转曲面方程的建立; 3.椭球面、双曲面和抛物面的标准方程。 1. 平时课堂表现、作业 完成情况 2. 期末考试 (五)课程考核方法 1. 平时课堂表现、作业完成情况 (30%) 2. 期末考试(闭卷,70%) (六)课程成绩评定方法及其与课程学习目标的关系 平时课堂表现、作业完成情况(30%)、期末考试(闭卷,70%) 课程学习目标 成绩评定方法 期末考试(闭卷) 课程分目标达成评价方法 课程学习目标 1 约 70% 分目标达成度=0.3×(平时课堂表现、作 业完成情况)+0.7×(期末考试) 课程学习目标 2 约 15% 课程学习目标 3 约 15% 合计 100 (七)课程学习目标与评分标准的对应关系 课程学习目标 评分标准 90-100 80-89 60-79 0-59 优 良 中/及格 不及格 课程学习目标 1 1 能准确理解向量及与 之有关的概念。熟练掌握 1 理解向量及与之 有关的概念。掌握向 1 基本理解向量及 与之有关的概念。基 对于空间解析几何的 基本概念、基本理论 7

向量的运算与向量乘法、量的运算与向量乘本掌握向量的运算与和求轨迹方程的方法 数量积、向量积、混合积法、数量积、向量向量乘法、数量积、 掌握比较欠缺。 和双重向量积的概念与性积、混合积和双重向向量积、混合积和双 质,向量共线、共面的充量积的概念与性质,重向量积的概念与性 要条件,在直角坐标系向量共线、共面的充质,向量共线、共面 下,用坐标进行向量的运腰条件,在直角坐标的充要条件,在直角 算。 系下,用坐标进行向坐标系下,用坐标进 ② 了解平面曲线、空间量的运算。 行向量的运算 曲线和曲面的概念。熟练②了解平面曲线、②了解平面曲线、 掌握曲线(或曲面)的参数空间曲线和曲面的概空间曲线和曲面的概 方程与普通方程的相互转念。掌握曲线(或曲念。基本掌握曲线(或 化,给出轨迹求方程。 面)的参数方程与普通曲面)的参数方程与普 ③能准确理解平面的法方程的相互转化,给通方程的相互转化, 向量,离差,直线的方向出轨迹求方程。 给出轨迹求方程。 向量、方向角、方向余弦③能理解平面的法能基本理解平面的法 和方向数,异面直线的距向量,离差,直线的向量,离差,直线的 离和公垂线的概念。熟练方向向量、方向角、方向向量、方向角、 掌握两平面相交、平行、方向余弦和方向数, 方向余弦和方向数, 重合的条件,直线与平面异面直线的距离和公异面直线的距离和公 相交、平行以及直线在平垂线的概念。掌握两垂线的概念。基本掌 面上的条件,直线与直线平面相交、平行、重 握两平面相交、平 异面、共面、相交、平合的条件,直线与平行、重合的条件,直 行、垂直、重合的条件。面相交、平行以及直线与平面相交、平行 能熟练求出平面(或直线在平面上的条件,以及直线在平面上的 线)的各种形式的方程,直线与直线异面、共条件,直线与直线异 点与平面的离差,直线的面、相交、平行、垂面、共面、相交、平 般方程与对称式方程的直、重合的条件。能行、垂直、重合的条 相互转化,公垂线方程,求出平面(或直线) 件。能基本求出平面 平面束中的一个平面。 的各种形式的方程, (或直线)的各种形 4 能准确理解柱面、柱点与平面的离差,直式的方程,点与平面 面的方向、准线和母线,线的一般方程与对称的离差,直线的一般 锥面、锥面的顶点、准线式方程的相互转化, 方程与对称式方程的 和母线,旋转曲面、旋转公垂线方程,平面束相互转化,公垂线方 曲面的旋转轴和母线的概中的一个平面。 程,平面束中的一个 念。熟练掌握椭球面、双④能理解柱面、柱 平面。 曲面和抛物面的概念及其面的方向、准线和母③能基本理解柱 性质,以直线族研究单叶线,锥面、锥面的顶面、柱面的方向、准 双曲面和双曲抛物面。 点、准线和母线,旋线和母线,锥面、锥 ⑤了解二次曲线按其渐转曲面、旋转曲面的面的顶点、准线和母 近方向或中心的分类。能旋转轴和母线的概线,旋转曲面、旋转 准确理解二次曲线的渐近念。掌握椭球面、双曲面的旋转轴和母线 方向、中心、奇异点、正曲面和抛物面的概念的概念。基本掌握椭 常点、渐近线和切线的概及其性质,以直线族球面、双曲面和抛物
向量的运算与向量乘法、 数量积、向量积、混合积 和双重向量积的概念与性 质,向量共线、共面的充 要条件,在直角坐标系 下,用坐标进行向量的运 算。 2 了解平面曲线、空间 曲线和曲面的概念。熟练 掌握曲线(或曲面)的参数 方程与普通方程的相互转 化,给出轨迹求方程。 3 能准确理解平面的法 向量,离差,直线的方向 向量、方向角、方向余弦 和方向数,异面直线的距 离和公垂线的概念。熟练 掌握两平面相交、平行、 重合的条件,直线与平面 相交、平行以及直线在平 面上的条件,直线与直线 异面、共面、相交、平 行、垂直、重合的条件。 能熟练求出平面(或直 线)的各种形式的方程, 点与平面的离差,直线的 一般方程与对称式方程的 相互转化,公垂线方程, 平面束中的一个平面。 4 能准确理解柱面、柱 面的方向、准线和母线, 锥面、锥面的顶点、准线 和母线,旋转曲面、旋转 曲面的旋转轴和母线的概 念。熟练掌握椭球面、双 曲面和抛物面的概念及其 性质,以直线族研究单叶 双曲面和双曲抛物面。 5 了解二次曲线按其渐 近方向或中心的分类。能 准确理解二次曲线的渐近 方向、中心、奇异点、正 常点、渐近线和切线的概 量 的 运 算 与 向 量 乘 法 、 数 量 积 、 向 量 积、混合积和双重向 量积的概念与性质, 向量共线、共面的充 要条件,在直角坐标 系下,用坐标进行向 量的运算。 2 了解平面曲线、 空间曲线和曲面的概 念。掌握曲线(或曲 面)的参数方程与普通 方程的相互转化,给 出轨迹求方程。 3 能理解平面的法 向量,离差,直线的 方向向量、方向角、 方向余弦和方向数, 异面直线的距离和公 垂线的概念。掌握两 平面相交、平行、重 合的条件,直线与平 面相交、平行以及直 线在平面上的条件, 直线与直线异面、共 面、相交、平行、垂 直、重合的条件。能 求出平面(或直线) 的各种形式的方程, 点与平面的离差,直 线的一般方程与对称 式方程的相互转化, 公垂线方程,平面束 中的一个平面。 4 能理解柱面、柱 面的方向、准线和母 线,锥面、锥面的顶 点、准线和母线,旋 转曲面、旋转曲面的 旋 转 轴 和 母 线 的 概 念。掌握椭球面、双 曲面和抛物面的概念 及其性质,以直线族 本掌握向量的运算与 向量乘法、数量积、 向量积、混合积和双 重向量积的概念与性 质,向量共线、共面 的充要条件,在直角 坐标系下,用坐标进 行向量的运算 2 了解平面曲线、 空间曲线和曲面的概 念。基本掌握曲线(或 曲面)的参数方程与普 通方程的相互转化, 给出轨迹求方程。 能基本理解平面的法 向量,离差,直线的 方向向量、方向角、 方向余弦和方向数, 异面直线的距离和公 垂线的概念。基本掌 握两平面相交、平 行、重合的条件,直 线与平面相交、平行 以及直线在平面上的 条件,直线与直线异 面、共面、相交、平 行、垂直、重合的条 件。能基本求出平面 (或直线)的各种形 式的方程,点与平面 的离差,直线的一般 方程与对称式方程的 相互转化,公垂线方 程,平面束中的一个 平面。 3 能 基 本 理 解 柱 面、柱面的方向、准 线和母线,锥面、锥 面的顶点、准线和母 线,旋转曲面、旋转 曲面的旋转轴和母线 的概念。基本掌握椭 球面、双曲面和抛物 和求轨迹方程的方法 掌握比较欠缺。 8

念。能熟练求出二次曲线研究单叶双曲面和双面的概念及其性质, 的渐近线、切线和直径。 曲抛物面。 以直线族研究单叶双 能准确判断二次曲线与直⑤能理解二次曲线曲面和双曲抛物面。 线的相关位置。 的渐近方向、中心、④能基本理解二次 奇异点、正常点、渐曲线的渐近方向、中 近线和切线的概念。心、奇异点、正常 能求出二次曲线的渐点、渐近线和切线的 近线、切线和直径。概念。能基本求出 会判断二次曲线与直次曲线的渐近线、切 线的相关位置。 线和直径。会判断 些二次曲线与直线的 相关位置。 ① 能熟练用向量法求三①能用向量法求三 ①基本会用向量法 对于用向量法求三角 角形和平行四边形的面角形和平行四边形的 求三角形和平行四边 形和平行四边形的面 积,平行六面体的体积,面积,平行六面体的 形的面积,平行六面 积,平行六面体的体 以及进行有关的几何证体积,以及进行有关体的体积,以及进行 积,以及进行有关的 明: 的几何证明: 些简单的几何证 几何证明:求点到平 ②能熟练求出点到平面②能求出点到平面明: 面(或直线)的距 (或直线)的距离,面与(或直线)的距离,②能基本求出点到 离,面与面、线与线 面、线与线和线与面的距面与面、线与线和线平面(或直线)的距 和线与面的距离,直 离,直线与直线、平面与与面的距离,直线与离,面与面、线与线 线与直线、平面与平 课程学习目标2 平面和直线与平面的夹直线、平面与平面和和线与面的距离,直 面和直线与平面的夹 角: 直线与平面的夹角: 线与直线、平面与平 角:曲线、平面、柱 能熟练画出曲线、平③能画出曲线、平面和直线与平面的夹 面、锥面、旋转曲 面、柱面、锥面、旋转曲面、柱面、锥面、旋角: 面、椭球面、双曲面 面、椭球面、双曲面和抛转曲面、椭球面、双③ 能基本画出曲 和抛物面的图形缺乏 物面的图形。 曲面和抛物面的图线、平面、柱面、锥 了解与掌握。 形。 面、旋转曲面、椭球 面、双曲面和抛物面 的图形。 ①熟练掌握曲线(或曲O掌握曲线(或曲( ①基本掌握曲线 对于曲线(或曲面) 面)的一般方程与参数方面)的一般方程与参 (或曲面)的一般方 的方程,柱面、锥面 程的转化: 数方程的转化: 程与参数方程的转 和旋转曲面方程的建 ②熟练掌握柱面、锥面② 掌握柱面、锥面化: 立,椭球面、双曲面 和旋转曲面方程的建立: 和旋转曲面方程的建 ②基本掌握柱面、 和抛物面的标准方程 课程学习目标3 ③熟练掌握椭球面、双立: 锥面和旋转曲面方程 缺乏了解和掌握。 曲面和抛物面的标准方③掌握椭球面、双【 的建立: 程。 曲面和抛物面的标准 ③基本掌握椭球 方程。 面、双曲面和抛物面 的标准方程。 9
念。能熟练求出二次曲线 的渐近线、切线和直径。 能准确判断二次曲线与直 线的相关位置。 研究单叶双曲面和双 曲抛物面。 5 能理解二次曲线 的渐近方向、中心、 奇异点、正常点、渐 近线和切线的概念。 能求出二次曲线的渐 近线、切线和直径。 会判断二次曲线与直 线的相关位置。 面的概念及其性质, 以直线族研究单叶双 曲面和双曲抛物面。 4 能基本理解二次 曲线的渐近方向、中 心 、 奇 异 点 、 正 常 点、渐近线和切线的 概念。能基本求出二 次曲线的渐近线、切 线和直径。会判断一 些二次曲线与直线的 相关位置。 课程学习目标 2 1 能熟练用向量法求三 角形和平行四边形的面 积,平行六面体的体积, 以及进行有关的几何证 明; 2 能熟练求出点到平面 (或直线)的距离,面与 面、线与线和线与面的距 离,直线与直线、平面与 平面和直线与平面的夹 角; 3 能熟练画出曲线、平 面、柱面、锥面、旋转曲 面、椭球面、双曲面和抛 物面的图形。 1 能用向量法求三 角形和平行四边形的 面积,平行六面体的 体积,以及进行有关 的几何证明; 2 能求出点到平面 (或直线)的距离, 面与面、线与线和线 与面的距离,直线与 直线、平面与平面和 直线与平面的夹角; 3 能画出曲线、平 面、柱面、锥面、旋 转曲面、椭球面、双 曲 面 和 抛 物 面 的 图 形。 1 基本会用向量法 求三角形和平行四边 形的面积,平行六面 体的体积,以及进行 一些简单的几何证 明; 2 能基本求出点到 平面(或直线)的距 离,面与面、线与线 和线与面的距离,直 线与直线、平面与平 面和直线与平面的夹 角; 3 能基本画出曲 线、平面、柱面、锥 面、旋转曲面、椭球 面、双曲面和抛物面 的图形。 对于用向量法求三角 形和平行四边形的面 积,平行六面体的体 积,以及进行有关的 几何证明;求点到平 面 ( 或 直 线 ) 的 距 离,面与面、线与线 和线与面的距离,直 线与直线、平面与平 面和直线与平面的夹 角;曲线、平面、柱 面 、 锥 面 、 旋 转 曲 面、椭球面、双曲面 和抛物面的图形缺乏 了解与掌握。 课程学习目标 3 1 熟练掌握曲线(或曲 面)的一般方程与参数方 程的转化; 2 熟练掌握柱面、锥面 和旋转曲面方程的建立; 3 熟练掌握椭球面、双 曲面和抛物面的标准方 程。 1 掌握曲线(或曲 面)的一般方程与参 数方程的转化; 2 掌握柱面、锥面 和旋转曲面方程的建 立; 3 掌握椭球面、双 曲面和抛物面的标准 方程。 1 基本掌握曲线 (或曲面)的一般方 程与参数方程的转 化; 2 基本掌握柱面、 锥面和旋转曲面方程 的建立; 3 基本掌握椭球 面、双曲面和抛物面 的标准方程。 对于曲线(或曲面) 的方程,柱面、锥面 和旋转曲面方程的建 立,椭球面、双曲面 和抛物面的标准方程 缺乏了解和掌握。 9