医用高等数学第7版 说课 0 知识点名称: 型未定式的洛必达法则 作者: 单位: 人民卫宝敛版社 PEOPLE'S MEDICAL PUBLISHING HOUSE
全国高校数学微课程教学设计竞赛 作者 : 单位 : 说 课 知识点名称: 型未定式的洛必达法则 0 0 医用高等数学第7版
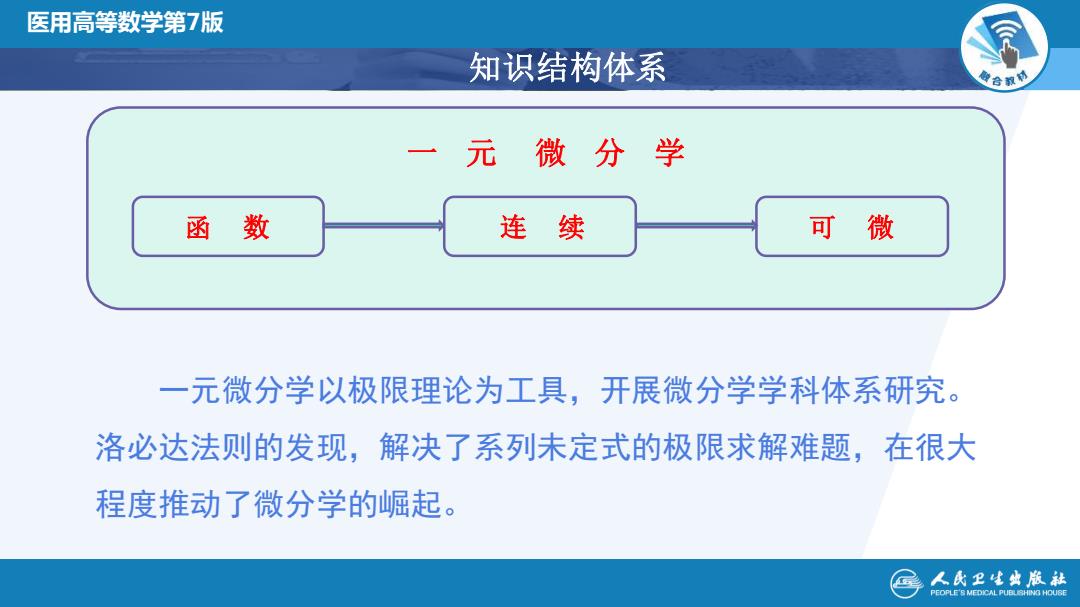
医用高等数学第7版 知识结构体系 色合教0 一元微分学 函数 连续 可微 一元微分学以极限理论为工具,开展微分学学科体系研究。 洛必达法则的发现,解决了系列未定式的极限求解难题,在很大 程度推动了微分学的崛起。 人民卫生典版社 PEOPLE'S MEDICAL PUBUSHING HOUSE
全国高校数学微课程教学设计竞赛 知识结构体系 一 元 微 分 学 连 续 医用高等数学第7版 函 数 可 微 一元微分学以极限理论为工具,开展微分学学科体系研究。 洛必达法则的发现,解决了系列未定式的极限求解难题,在很大 程度推动了微分学的崛起

医用高等数学第7版 教学目标 色合教0 知识 未定式的分类、洛必达法则 能力 熟练运用洛必达法则、培养学生创新实践能力 情感 提升学生学习数学的兴趣 人民卫生典版社 PEOPLE'S MEDICAL PUBLSHING HOUSE
全国高校数学微课程教学设计竞赛 能力 情感 知识 未定式的分类、洛必达法则 熟练运用洛必达法则、培养学生创新实践能力 提升学生学习数学的兴趣 医用高等数学第7版 教学目标

医用高等数学第7版 教学内容 色合教0 重点难点 掌握 未定式的分类和洛必达法则 熟悉 洛必达法则求极限的方法 了解 洛必达法则在带参函数模型中的应用 人民卫生典版社 PEOPLE'S MEDICAL PUBLSHING HOUSE
全国高校数学微课程教学设计竞赛 重点难点 熟悉 了解 掌握 未定式的分类和洛必达法则 洛必达法则求极限的方法 洛必达法则在带参函数模型中的应用 教学内容 医用高等数学第7版
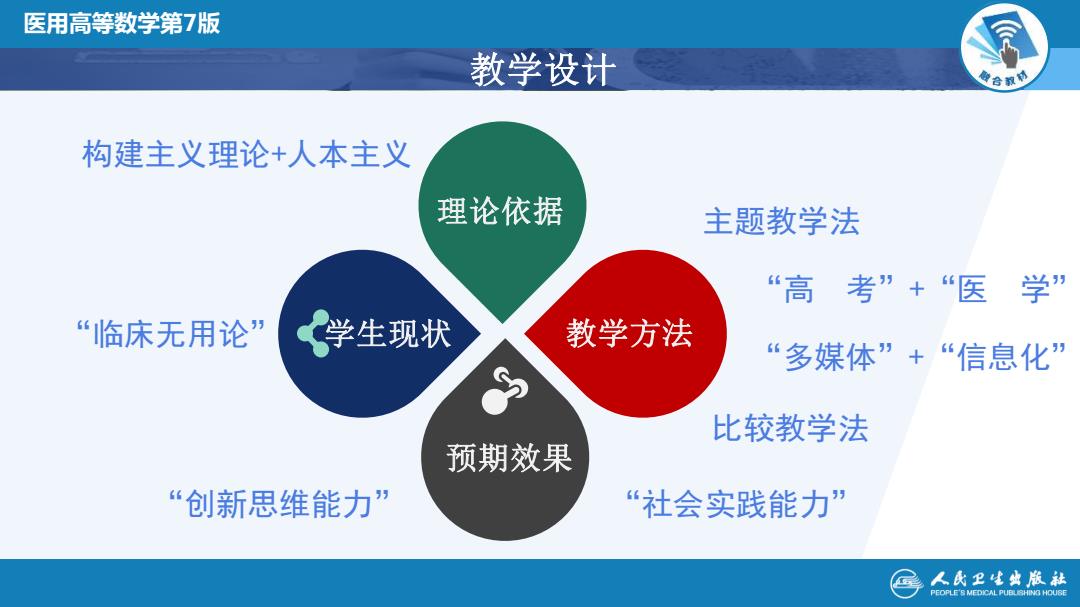
医用高等数学第7版 教学设计 色合教0 构建主义理论+人本主义 理论依据 主题教学法 “高考”+“医学” “临床无用论 学生现状 教学方法 “多媒体”+“信息化” 比较教学法 预期效果 “创新思维能力” “社会实践能力” 人民卫生典版社 PEOPLE'S MEDICAL PUBUSHING HOUSE
全国高校数学微课程教学设计竞赛 医用高等数学第7版 教学设计 学生现状 教学方法 理论依据 预期效果 构建主义理论+人本主义 主题教学法 “临床无用论” “创新思维能力” “社会实践能力” “高 考”+“医 学” “多媒体”+“信息化” 比较教学法

医用高等数学 安徽联盟高校同课异构教学竞赛 色合教0 0 知识点名称: 型未定式的洛必达法则 作者: 谷 单位: 人民卫建典版社 PEOPLE'S MEDICAL PUBUSHING HOUSE
全国高校数学微课程教学设计竞赛 医用高等数学 作者 : 单位 : 知识点名称: 型未定式的洛必达法则 0 0 安徽联盟高校同课异构教学竞赛
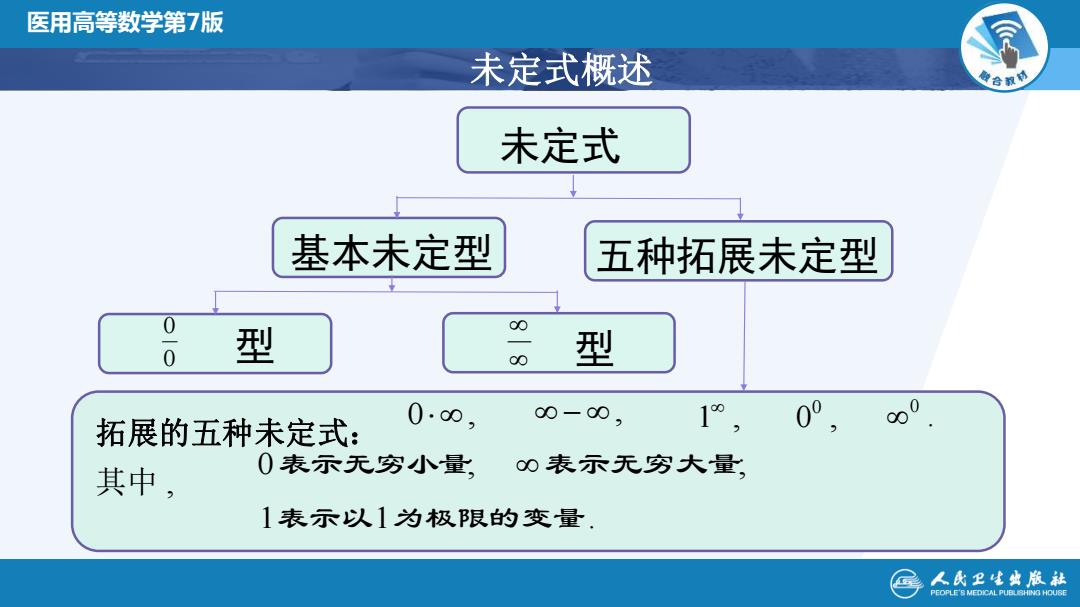
医用高等数学第7版 未定式概述 色合教0 未定式 基本未定型 五种拓展未定型 0 00 0 型 00 型 拓展的五种未定式: 0.0, 00-00, 1°, 00 00 其中, 0表示无穷小量 0表示无穷大量 1表示以1为极限的变量. 人民卫生典版社 PEOPLE'S MEDICAL PUBUSHING HOUSE
全国高校数学微课程教学设计竞赛 未定式概述 型 未定式 基本未定型 五种拓展未定型 0 型 0 0 , − , 1 , 0 , 0 . 0 其中 , 0表示无穷小量; 表示无穷大量; 1表示以1为极限的变量. 拓展的五种未定式: 医用高等数学第7版

医用高等数学第7版 教学主题 思合教0 。型未定式的洛必达法则应用 之高考函数摸型求解 人民卫建典版社 PEOPLE'S MEDICAL PUBUSHING HOUSE
全国高校数学微课程教学设计竞赛 医用高等数学第7版 型未定式的洛必达法则应用 之高考函数模型求解 0 0 教 学 主 题

医用高等数学第7版 问题背景 生物益生菌有益于人体胃肠 道健康。统计研究发现,在特 定的温度环境下,其保质期服 2 从某函数分布。 在已知函数模型及特定条件,如何确定保存温度? 人民卫生典版社 PEOPLE'S MEDICAL PUBLSHING HOUSE
全国高校数学微课程教学设计竞赛 问 题 背 景 生物益生菌有益于人体胃肠 道健康。统计研究发现,在特 定的温度环境下,其保质期服 从某函数分布。 在已知函数模型及特定条件,如何确定保存温度? 医用高等数学第7版

医用高等数学第7版 洛必达法则 色合教0 设在某一极限过程中 0 (1)lim f(x)=0,limg(x)=0, 0 00 lim f(x)=co,limg(x)=o, 00 (2)在该极限过程中,f'(x),g'(x)存在,且g'(x)≠0, (3)lim f'(x) 存在或为无穷大, 今天主要讲述。型洛必 g'(x) 达法则在函数带参问题中 则有 lim 1x) lim '(x) 8(x) g'(x) 的实践价值和解题效度 人民卫生典版社 PEOPLE'S MEDICAL PUBUSHING HOUSE
全国高校数学微课程教学设计竞赛 设在某一极限过程中 0 0 (1) lim f (x) = 0 , lim g(x) = 0 , lim ( ) , lim ( ) , f x = g x = (2) 在该极限过程中, f (x), g (x)存在, 且 g (x) 0 , , ( ) ( ) (3) lim 存在或为无穷大 g x f x . ( ) ( ) lim ( ) ( ) lim g x f x g x f x 则有 = 洛 必 达 法 则 今天主要讲述 型洛必 达法则在函数带参问题中 的实践价值和解题效度. 0 0 医用高等数学第7版