
3.3定积分的应用 3.3.1微元法 3.3.2定积分在几何上的应用 3.3.3连续函数的平均值 3.3.4定积分在物理上的应用 涵 3.3.5定积分在医学上的应用
3.3.3 连续函数的平均值 3.3.1 微元法 3.3 定积分的应用 3.3.2 定积分在几何上的应用 3.3.4 定积分在物理上的应用 3.3.5 定积分在医学上的应用
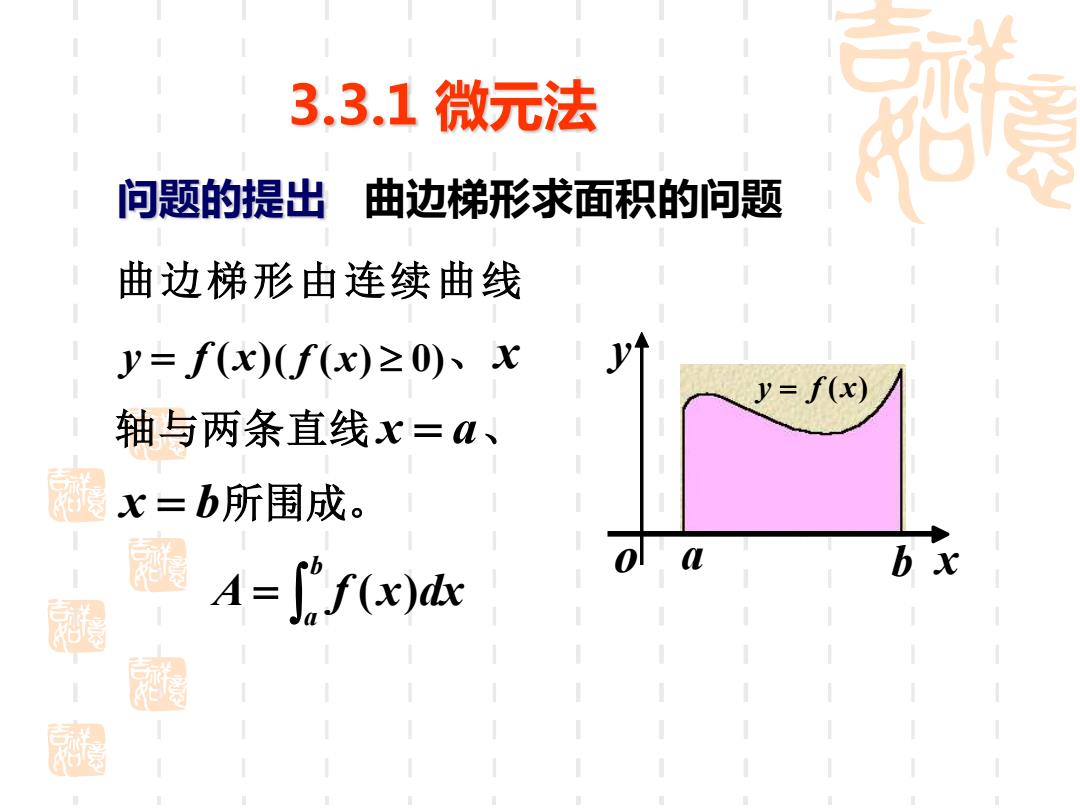
3.3.1微元法 问题的提出 曲边梯形求面积的问题 曲边梯形由连续曲线 y=f(x)(f(x)≥0)、x y=f(x) 轴与两条直线x=a、 调 x=b所围成。 冠A=f b x
曲边梯形求面积的问题 = b a A f (x)dx 曲边梯形由连续曲线 y = f (x)( f (x) 0)、x 轴与两条直线 x = a、 x = b所围成。 a b x y o y = f (x) 问题的提出 3.3.1 微元法

面积表示为定积分的步骤如下 (1)把区间[a,b]分成n个长度为△x,的小区间, 相应的曲边梯形被分为n个小窄曲边梯形,第i 个小窄曲边梯形的面积为△A,则A=∑△4, i=1 (2)计算△A的近似值 △A:≈f(5)△x:5:∈△x, (3)求和,得A的近似值A≈∑f(传)△x· i=1
面积表示为定积分的步骤如下 (1)把区间[a,b]分成n个长度为 i x 的小区间, 相应的曲边梯形被分为n个小窄曲边梯形,第i 个小窄曲边梯形的面积为 Ai,则 (2)计算Ai的近似值 i i xi A f ( ) i xi (3)求和,得A的近似值 ( ) . 1 i i n i A f x = = = n i A Ai 1

(4)求极限,得A的精确值 A=Iim∑f传)△x,=f(x)dc 元→0 i=1 面积元素 提示 若用△A表示任一小区间 [比,x+△上的窄曲边梯形的面积,' f(x) 则A=∑△A,并取△A≈f(x), 于是A≈∑f(x) A-limf()df()dx. o a xx+dx b x
a b x y o y = f (x) (4) 求极限,得A的精确值 i i n i A = f x = → lim ( ) 1 0 = b a f (x)dx 提示 若用A 表示任一小区间 [x, x + x]上的窄曲边梯形的面积, 则A = A,并取A f (x)dx, 于是 A f (x)dx A = lim f (x)dx ( ) . = b a f x dx x x + dx dA 面 积 元 素

观察上述四步我们发现,第2步最关键,因为最后的 被积表达式的形式就是在这一步被确定的,这只要把近似 式f(5)△x,中的变量记号改变一下即可(5换为x;△x,换为dc), 而后两步可以合并成一步:在区间4,b上无限累加, 即在[4,b上积分.至于第1步,它只是指明所求量具有可 加性,这是F能用定积分计算的前提,于是,上述四步 简化后形成实用的微元法
2 ( ) ( ; ). i i i i f x x x dx 观察上述四步我们发现,第 步最关键,因为最后的 被积表达式的形式就是在这一步被确定的,这只要把近似 式 中的变量记号改变一下即可 换为 换为 [ , ] [ , ] a b a b F 而后两步可以合并成一步:在区间 上无限累加, 即在 上积分.至于第1步,它只是指明所求量具有可 加性,这是 能用定积分计算的前提,于是,上述四步 简化后形成实用的微元法

微元法的一般步骤: 1)根据问题的具体情况,选取一个变量例如X为 积分变量,并确定它的变化区间[M,b]: 2)设想把区间a,b]分成n个小区间,取其中任一 小区间并记为x,x+,求出相应于这小区间的 部分量△A的近似值.如果△A能近似地表示为a,b] 潮 上的一个连续函数在x处的值f(x)与c的乘积, 就把f(x)dx称为量U的元素且记作A,即 dA=f(x)dx;
微元法的一般步骤: 1)根据问题的具体情况,选取一个变量例如x为 积分变量,并确定它的变化区间[a,b]; 2)设想把区间[a,b]分成 n 个小区间,取其中任一 小区间并记为[x, x + dx],求出相应于这小区间的 部分量A的近似值.如果A能近似地表示为[a,b] 上的一个连续函数在x处的值 f (x)与dx的乘积, 就把 f (x)dx称为量U的元素且记作dA,即 dA f x dx = ( ) ;

3)以所求量A的元素f(x)d为被积表达式,在 区间[a,b1上作定积分,得A=∫么f(x) 即为所求量A的积分表达式. 这个方法通常叫做微元分析法,简称微元法,又称 元素法。 应用方向: 平面图形的面积;体积;平面曲线的弧长;功; 水压力;引力和平均值等 。 #
3)以所求量 A 的元素 f (x)dx为被积表达式,在 区间[a,b]上作定积分,得 ( ) b a A f x dx = , 即为所求量 A 的积分表达式. 这个方法通常叫做微元分析法,简称微元法,又称 元素法。 应用方向: 平面图形的面积;体积;平面曲线的弧长;功; 水压力;引力和平均值等。 #
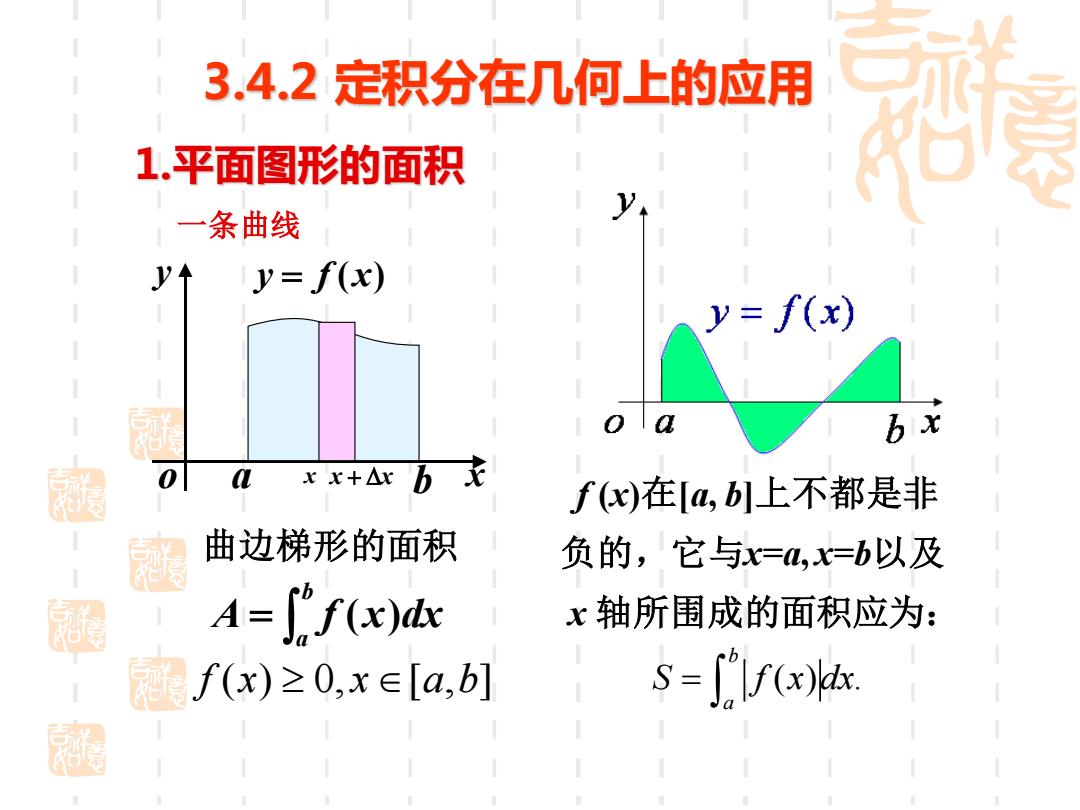
3.4.2定积分在几何上的应用 1.平面图形的面积 一条曲线 y=f(x) y=f(x) bx L xx+△ :b f(x)在[a,b]上不都是非 曲边梯形的面积 负的,它与x=4,x=b以及 湖 A=[f(x)dx x轴所围成的面积应为: f(x)≥0,x∈[a,b] s -["lf(x)x
x y o y = f (x) a b 曲边梯形的面积 = b a A f (x)dx x x + x 1.平面图形的面积 f x x a b ( ) 0, [ , ] f (x)在[a, b]上不都是非 x 轴所围成的面积应为: 负的,它与x=a, x=b以及 ( ) . b a S f x dx = 3.4.2 定积分在几何上的应用 一条曲线
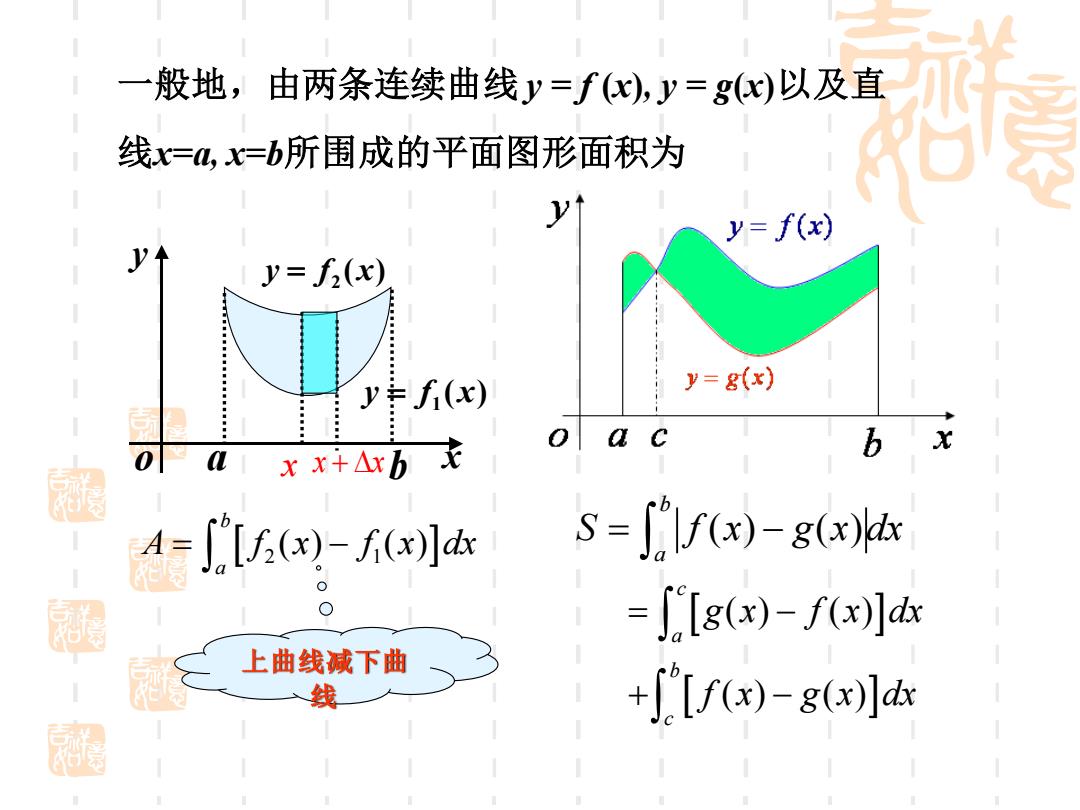
一 般地,由两条连续曲线y=f(x),y=gx)以及直 线x=4,x=b所围成的平面图形面积为 y=f(x) y=f(x) f(x) y y=g(x) a c 0 xx+△rbt A= 〔[(ax)-(x]d s=["lf(x)-g(x) 0 ∫[g(x)-f(x]dr 上曲线减下曲 线 +J[f(x)-g(x)]dx
( ) ( ) ( ) ( ) c a b c g x f x dx f x g x dx = − + − 一般地,由两条连续曲线 y = f (x), y = g(x)以及直 线x=a, x=b所围成的平面图形面积为 x y o ( ) y = f 1 x ( ) y = f 2 x a b 2 1 ( ) ( ) b a A f x f x dx = − x x x + 上曲线减下曲 线 ( ) ( ) b a S f x g x dx = −
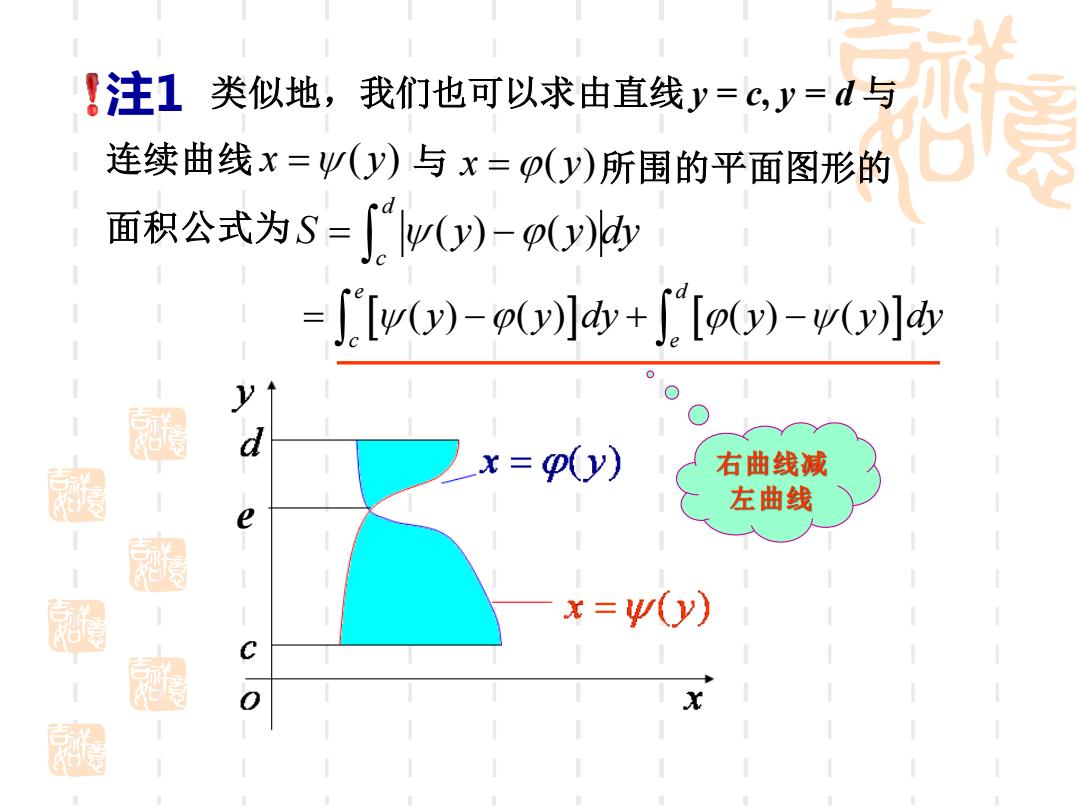
!注1类似地,我们也可以求由直线y=c,y=d与 连续曲线x=W(y)与x=p(y)所围的平面图形的 面积公式为S=∫(y)-o(y) ∫[w0)-p]+[o)-w(]d 0 y d x=o(y) 右曲线减 涵 左曲线 x=Ψ(y) X
( ) ( ) ( ) ( ) e d c e = − + − y y dy y y dy 注1 类似地,我们也可以求由直线 y = c, y = d 与 连续曲线 x y = ( ) 与 x y = ( ) 所围的平面图形的 面积公式为 右曲线减 左曲线 e ( ) ( ) d c S y y dy = −