
2.1导数的概念 2.1.1两个实例 2.1.2导数的定义 2.1.3导数的几何意义 凝 2.1.4函数的可导性与连续性之间的关系
2.1.1 两个实例 2.1.2 导数的定义 2.1.4 函数的可导性与连续性之间的关系 2.1 导数的概念 2.1.3 导数的几何意义

2.1.1两个实例 1、变速直线运动的瞬时速度(物理物体 ) 已知作变速直线运动物体的运动方程为5=5(). 当时刻t=t时,物体的位置坐标为so=s(t6) 问物体在时刻的瞬时速度是多少 分析:首先考虑物体在时刻附近很短一段时间内 的运动。 S T T to to+At
1、变速直线运动的瞬时速度(物理物体) 已知作变速直线运动物体的运动方程为s =s (t). 当时刻 t = t0 时,物体的位置坐标为s0= s( t0 ). 分析:首先考虑物体在时刻t0附近很短一段时间内 的运动。 2.1.1 两个实例 问物体在时刻t0的瞬时速度是多少 t0 t0 +Δt

当t从增加到t十△t时,相应地s在△这段时间 内的位移为△s=s(t,+△t)-s(), 而在△t时间内物体的平均速度为 △S s(to+At)-s(to)s(t)-s(to) △t △t t-to 随着△的减小,平均速度)就愈接近质点在时刻 t的瞬时速度(简称速度).但无论△t取得怎样小, 平均速度总不能精确刻画质点在时刻t=的运动 变化率
0 0 ( ) ( ) . s s t t s t v t t + − = = 而在 ∆t 时间内物体的平均速度为 随着∆t 的减小,平均速度 v 就愈接近质点在时刻 t0的瞬时速度(简称速度). 但无论∆t 取得怎样小, 平均速度总不能精确刻画质点在时刻 t = t0的运动 变化率。 0 0 ( ) ( ) . s t s t t t − = − 当 t 从 t0 增加到 t0+ ∆t 时,相应地s 在∆t这段时间 内的位移为 0 0 s = + s t t t ( ) ( ) − s

采取“极限”的手段:如果平均速度As 当 △t △t→0时的极限存在,则自然地把此极限(记为v) 定义为物体在t=时的瞬时速度或速度: v=lim △S lim s+△)-()=v() △t→0 △t △t-→0 △t 该极限值就是t时刻的瞬时速度y(t)
0 0 0 0 ( ) ( ) lim lim t t s s t t t v t t → → + − = = 采取“极限”的手段:如果平均速度 →t 0 时的极限存在, , s v t = 当 则自然地把此极限(记为v ) 定义为物体在t = t0 时的瞬时速度或速度: 该极限值就是t0 时刻的瞬时速度 v(t0 )。 = v t( 0 )

2、细胞的增殖速度(生物问题) 设细胞在某时刻t的总数为N(),在时刻t+△t的总数为 N(t+△t),细胞在△t时间内的平均增长率为: V= N(t+△)-N()△N(t) (t+△t)-t △t 当△→0时,平均增殖速度的极限就是细胞在时刻t的 瞬时增殖速度。 lim AN() lim N(t+△t)-N(t) △t→0 △t △t-→0 △t
设细胞在某时刻t 的总数为N(t),在时刻 t +∆t 的总数为 N(t +∆t ),细胞在∆t 时间内的平均增长率为: ( ) ( ) ( ) ( ) N t t N t N t V t t t t + − = = + − 当∆t →0时,平均增殖速度的极限就是细胞在时刻t 的 瞬时增殖速度。 ( ) 0 0 ( ) ( ) lim lim t t N t N t t N t t t → → + − = 2、细胞的增殖速度(生物问题)

3、曲线的切线斜率 (数学问题) y=f(x) 设曲线L的方程为 y=f(x),P(xo,yo) △y 1) 为L上的一个定点 yo 为求曲线y=fx)在 X0△x X 点P的切线,可在 曲线上取邻近于P的点P(x。+△x,y,+△y),算出 两 割线P,P的斜率:anB=A少-f+)-fC, △x △x
3、曲线的切线斜率 (数学问题) 0 0 P x x y y ( ) + + , , 设曲线L的方程为 0 0 0 y f x P x y = ( ) ( ) , , 为 L上的一个定点. 点 P0 的切线,可在 曲线上取邻近于P0 的点 割线 P0 P 的斜率: x y O y f x = ( ) 0 x 0 y x y y P0 P 为求曲线 y = f (x) 在 0 0 ( ) ( ) tan y f x x f x x x + − = = , 算出

割线的极限位置——切线位置 60 50 40 30 20 10 0 1.251.51.7522.252.52.753
割线的极限位置——切线位置
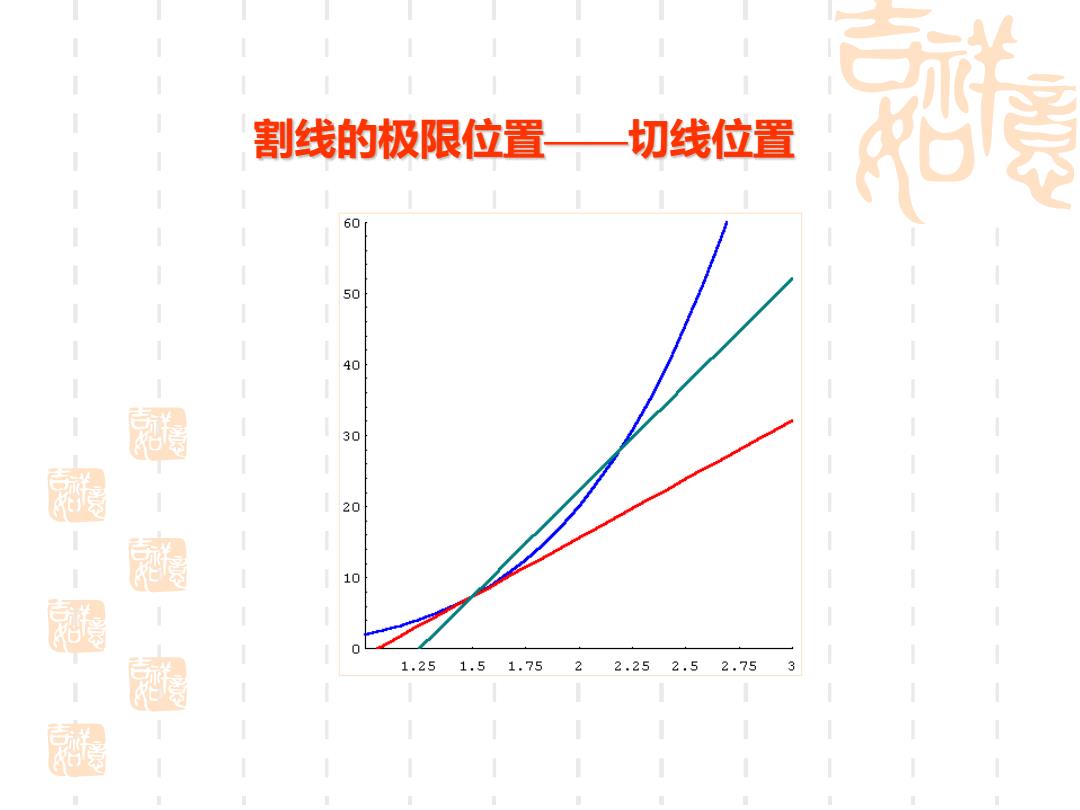
割线的极限位置——切线位置 60 50 40 30 20 10 0 1.251.51.7522.252.52.753
割线的极限位置——切线位置

割线的极限位置——切线位置 60 50 40 30 20 10 0 1.251.51.7522.252.52.753
割线的极限位置——切线位置
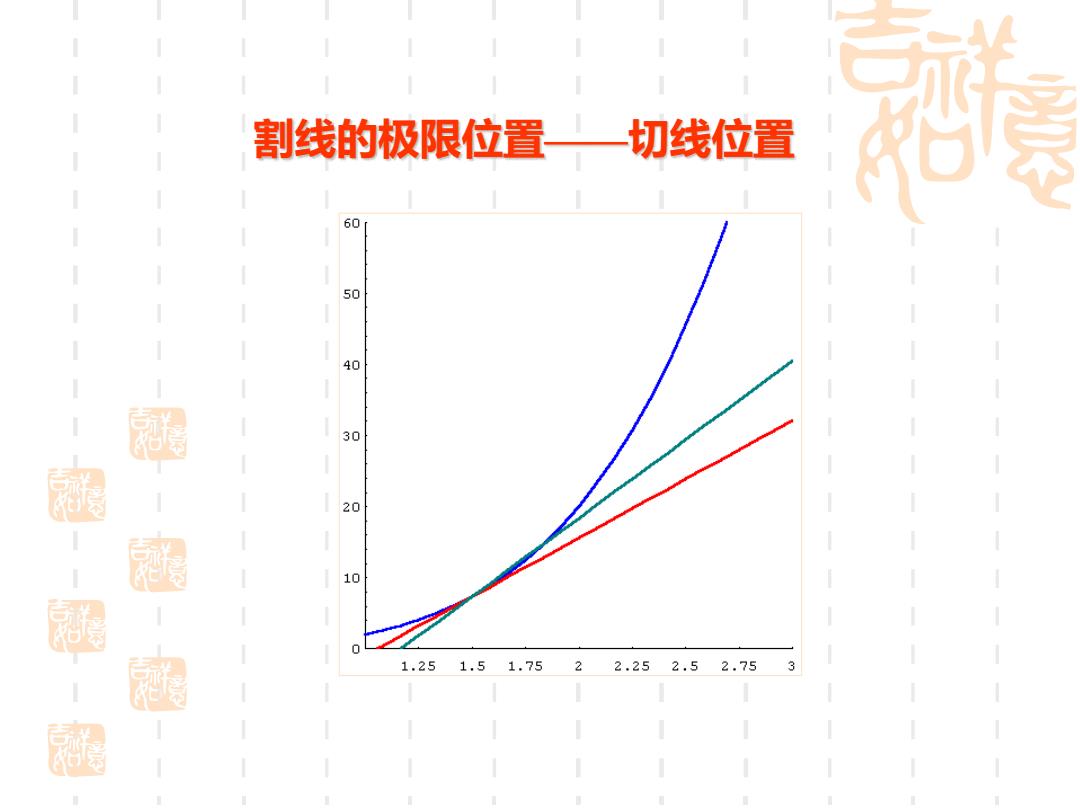
割线的极限位置——切线位置 60 50 40 30 20 10 0 1.251.51.7522.252.52.753
割线的极限位置——切线位置