
第1章向量与坐标 §1.1向量的概念 1.下列情形中的向量终点各构成什么图形? (1)把空间中一切单位向量归结到共同的始点: (2)把平行于某一平面的一切单位向量归结到共同的始点: (3)把平行于某一直线的一切向量归结到共同的始点: (4)把半行于某一直线的一切单位向量归结到共同的始点, [解]:(1)单位球面: (2)单位圆 (3)直线: (4)相距为2的两点 2.设点O是正六边形ABCDEF的中心, 在向量OA、OB、OC、OD、OE、 OF、AB、BC、C⑦、D正、F B 和FA中,哪些向量是相等的? [解]:图1-1,在正六边形ABCDEF中, 相等的向量对是: 图1-1 OA和EF:OB和FA:OC和AB:OE和CD,OF和DE, 3.设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB.BC CD DA的中点,求证:KL=NM.当ABCD是空间四边形时,这等式是杏也成立? [证明]:如1图1-2,连结AC,则在△BAC中, 24C.K立与4C方向相同:布AD1C KL丛 中,NM丛AC.NM与AC方向相同,从而 KL=NM A.KL与NM方向相同,所以KL= NM. 4.如图1-3,设ABCD-EFGH是一个平行六面 体,在下列各对向量中,找出相等的向量和 B 互为相反向量的向量: (1)AB、CD:(2)AE、CG: (3) AC、EG: (4)AD、GF: (S)BE、Ca [解]:相等的向量对是(2)、(3)和(5): 图1—3 互为反向量的向量对是(1)和(4)。 §1.3 数量乘向量 1.要使下列各式成立,向量a,b应满足什么条件? )后+=6- (2)a+=+时 (3)后+=同- (4)后--同+

(5)--=日- [解]:(1)a,b所在的直线垂直时有a+--: (2)a.i同向时有6+=同+例 (3)同≥尽且a,6反向时有后+=- (4)a,6反向时有后-=日+ (5)a,b同向,1 同≥时有6-=同-风 2.设L、M、N分别是△ABC的三边BC、CA、AB的中点,证明:三中线向量AL BM CN 可以构成一个三角形 [证明]: AL=(4B+C) 所-+G CN =(CA+CB) :.AL+BM+CN=-(4B+4C+BA+BC+C4+CB)=0 从而三中线向量AL,BM,CN构成一个三角形。 3.设L、M、N是△ABC的三边的中点,O是任意一点,证明 OA+OB+OC=OL+OM+ON [证明]OA=OL+LA OB =OM+MB OC-ON+NC ..OA+OB+OC =OL+OM+ON+(LA+MB+NC) =OL+OM+ON-(AL+BM+CN) 山上题结论知:AL+BM+CN=0 ..0A+0B+OC=OL+OM+ON 4.用向量法证明,半行四边行的对角线互相兴分. [证明]:图1-4,在半行四边形ABCD中,O是对角线AC,BD的交点 D AD=OD-OA BC=OC-OB /0 但AD=BC ·.OD-OA=OC-OB 图1-4 OA+OC=OD+0B 山于(OA+OC)∥AC,(OB+OD)∥BD,而AC不半行于BD, ...0A+OC=OD+0B=0, 从而OA=OC,OB=OD
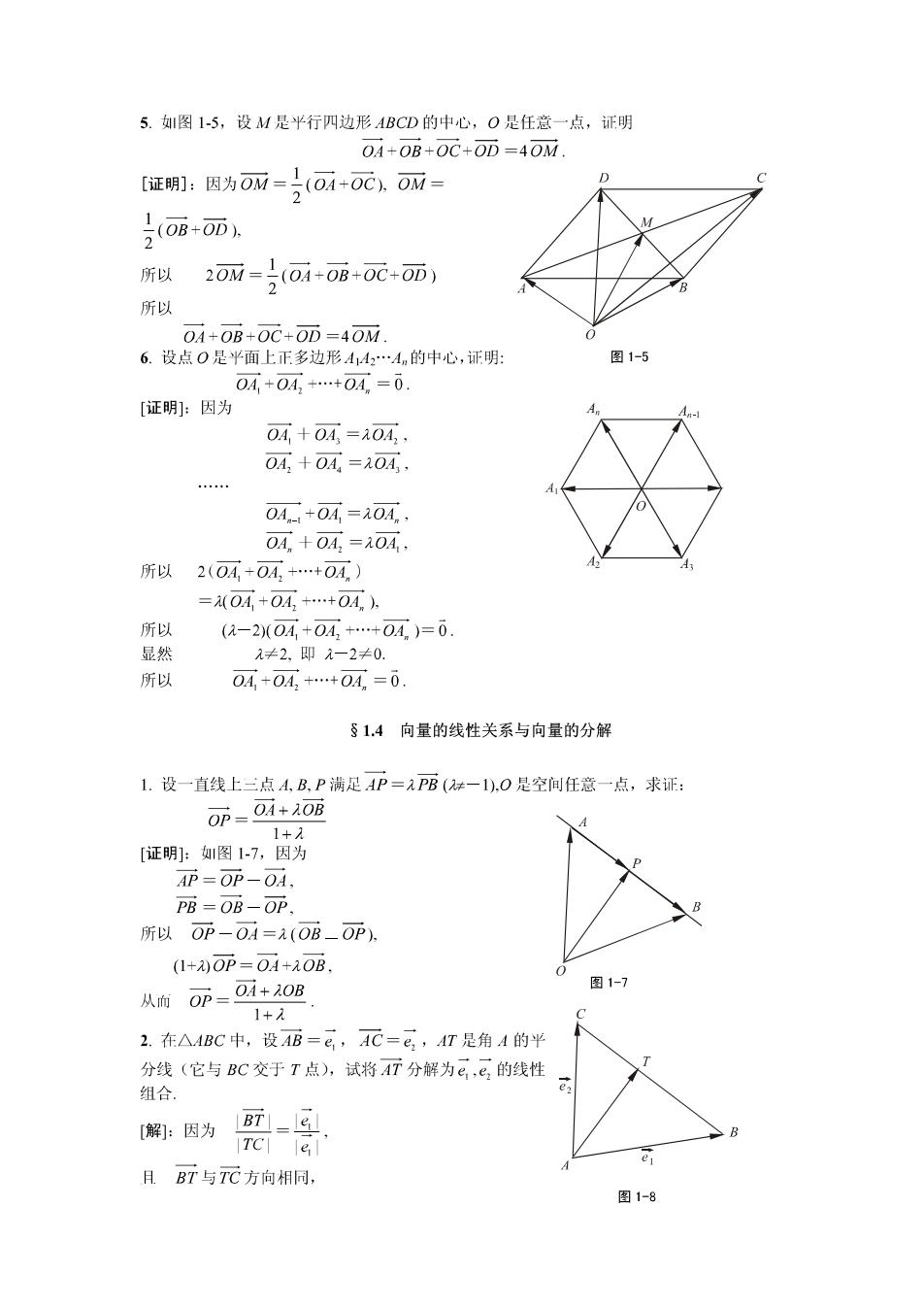
5.1图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明 0A+0B+0C+OD=40M [证明]:因为OM=(OA+0C,OM= 0 08-0 M 所以 20丽-0i+0+0元+0n, 所以 0A+0B+OC+OD =40M 0 6.设点O是平面上正多边形A142…An的中心,证明: 图1-5 OA,+OA2+…+OAn=0 [证明]:因为 OA+04,=104,, 0A,+0A=20A, *… 0An+0A=0A. OA,+04,=104,, 所以2(OA,+OA,++OA,) =(OA,+OA2+…+OA。)片 所以 (1-2(0A,+0A,+…+0A)=0 显然 ≠2.即元-2≠0. 所以 0A+0A,++0A=0 §1.4向量的线性关系与向量的分解 1.设一直线上三点A,B,P满足AP=元PB(+一1),O是空间任意一点,求证: 0p- OA+OB 1+ [证明]:图1-7,因为 AP=OP-OA, PB=OB-OP 所以OP-OA=(OB-OP). (1+)OP=04+1OB 从而 0p=O1+20B 图1-7 1+元 2.在△4BC中,设AB=e,AC=G,AT是角A的平 分线(它与BC交于T点),试将AT分解为e,C,的线性 组合 [解]:因为 BTe 月BT与TC方向相同, 图1-8

所以 B7=ST元 e 山上题结论有 e+ e -e, A7= e, le,le+lele, 1+19 le+le, e, 3.用向量法证明:P是△ABC重心的充要条件是 PA+PB+PC=0 [证明]:“三”若P为△ABC的重心,则 CP=2PE=PA+PB. 图1-9 从而PA+PB-CP=0. 即PA+PB+PC=0. “∈”若PA+PB十PC=0, 则PA+PB=一PC=CP 取E,F,G分别为AB,BC,CA之中点,则有 PE=(P4+PB). 从而CP=2PE. 同理可证BP=2PG,AP=2PF.故P为△ABC的重心. 4.证明三个向量a=-g,+3e,+2e,b=4e,-6e,+2e,c=-3e,+12e,+11g共面, 其中a能杏用b,c线性表示?能表示,写出线性表示关系式. [证明]:山于向量,e,g不共面,即它们线性无关. 考虑表达式a+ub+vc=0,即 1(-e+3e+2e)+u(4e,-6e,+2e,)+v(-3e,+12e十11e)=0, 或(-2+4-3v)e,+(32-6u+12)e2+(2+2u+11)e=0. 山于e,,g线性无关,故有 -1+44-3y=0, 31-6十12y=0, 2元+24+11v=0. 解得2=-10,u=-1,v=2. 山于1=一10≠0,所以ā能用b,c线性表示 a=-05+5 10 5.图1-10,OA,OB,OC是二个两两不共线的向量,月OC=OA+uOB,试证A,B,C 三点共线的充要条件是+u=1. B [证明]:“→”因为A,B,C共线,从而有 AC//CB. 月有m≠一1,使AC=mCB, OC-OA=m (OB-OC). (1+m)OC=0A+mOB, 图1-10

0c=,101+,m0B 1+m 1+m 但已知OC=1OA+uOB.山OC对OA,OB分解的唯一性可得 ≈、1 、n 1+m 1+m 1+m=1. 从而左4一十m1+m “=”设+u=1.则有OC=OA十uOB=AOA十(1-)OB =OB+(OA-OB). OC-OB=(OA-OB), 所以BC=1BA」 从而BC∥BA. 故A,B,C三点共线。 §1.5标架与坐标 1.在空间直角坐标系{O:i,j,k}下,求P(2.一3,一1),Ma.b,c)关于 (1)坐标平面:(2)坐标轴:(3)坐标原点的各个对称点的坐标. [解]:M(a,b,c)关于xOy平面的对称点坐标为(a,b,一c), M(a,b,c)关于yOz平面的对称点坐标为(一a,b,c), M(a,b,c关于xOz半面的对称点坐标为(a,一b.c), M(a,b,c)关于x轴平面的对称点坐标为(a,一b,一c), M(a,b,c)关于y轴的对称点的坐标为(一a,b,一c), M(a,b,c)关于z轴的对称点的坐标为(一a,一b,c). 类似考虑P(2,-3,-1)即可. 2.已知向量a,b,c的分量如1下: (1)a={0,-1,2,i=0,2,-4},c={1,2,-1: (2)a={1,2,3},b={2,-1,0},c={0,5,6. 试判别它们是杏共面?能杏将c表成a,b的线性组合?若能表示,写出表示式. 0-1 2 [解](1)因为 02 -4 0.所以a,6,c三向量共面, 1 2 -1 又因为a,b的对应坐标成比例,即a1b,但c次a, 故不能将c表成a,b的线性组合 123 (2)因为2-10=0.所以a,6,c三向量共面 056 又因为a,方的对应坐标不成比例,即a石, 故可以将c表成a,b的线性组合. 设c=ā+ub,亦即{0,5,6}={1,2,3}+{2,一1,0} 从而

[1+24=0, 21-4=0, 3=6. 解得 =2,1=-1, 所以 c=2a-b 3.证明:四面体每一个项点与对面重心所连的线段共点,月这点到顶点的距离是它到对面重 心距离的二倍.用四面体的顶点坐标把交点坐标表示出来 [证明]:设四面体A14444A:对面重心为G.欲证A,G交于一点(i=1,2,3,4). 在4,G上取一点P,使4P=3PG,从而OP= OA +30G 1+3 设4(c,y,z(i=1,2,3,4),则 G x3+x3+x4当3+y3+y4 Z3+23+24 3 3 3 G25+x+x4 当+3+y42+23+24 、3 3 3 +x+,上+少,+业, G 21+22+24 3 G4+x+5,凸+少+丛、名+z+a 3 3 3 所以 x+3++y+3.上++丛名+3名+名+2 P1( 3 3 3一) 1+3 1+3 1+3 =P,(+++,+乃++y,名+名++区)】 4 4 4 同理得P=P=P4=P,所以AG:交于一点P,月这点到顶点距离等于这点到对面重心距离的 二倍. §1.6向量在轴上的射影 L.已知向量AB与单位向量e的夹角为150°,月AB-10,求射影向量:AB与射影:AB, 又如果e=e,求射影向量。AB与射影AB [解] 射影:AB=ABcos∠(e,AB)=10.COS150°=-5V5, 射影向量AB=-5V3e e=-e,∠(e,AB)=180-∠(e,AB)=30 ∴.射影元AB=AB cos∠(e,AB)=10.COS30°=5V3

射影向量。AB=5√3e 2试证明:射影(2a+入a,++na)=射影a+,射影,a, ++入n射影1an [证明]:用数学归纳法来证 当n=2时,有 射影(21a,+2a,)=射影(2,a,)+射影(2,a2)=1射影1a+2射影1a2. 假设当n=k时等式成立,即有 射影(2,a+…+,a)=射影1a++射影a: 欲证当n=k+1时亦然.事实上 射影(元a,+…+a:+a) =射影(a+…+a)十1ak] =射影(,a,+…+a)十射影(a1) =射影a++元射影a+1射影1a 故等式对自然数n成立. §1.7两向量的数性积 1.证明 (1)向量a垂直于向量(ab)c-(ac)1b [证明]: (2)在平面上1果mm2,月ā·m,=b·m,(i=1,2),则有=b [证明]:因为m水m,所以,对该半面上任意向量c=1m,十4m, (a-b)c=(a-b)2m十um,) =m,(a-b)tum (a-b) =ia i -b in )+u a m2 -b m,)=0, 故(a-b)Lc. 山c的任意性知a一b=0 从而a=b 2.已知向量a,i五相垂直,向量c与a,6的夹角都是60,月同-1同-2,月-3计算: ①)(a+b)2;(2)(a+b)(a-b);(3)3a-2b).b-3c):4)(a+2b-c)2 [解]: a+i}=a+2a6+6=1+2×0+22=5 2)a+ba-b)=a+6=1-22--3 (3)3a-2b).(6-3c)=3a.b-2b-9ac+6i.c 日-8-9x3.c0s60+6×2x3c0s60=-7岁 (4a+26-c2=a+4ab-2ac-4bc+462+c =1-2×3c0s60°-4×2×3c0s60°+4×22+32=11

3.用向量法证明以下各题: (1)三角形的余弦定理a2=b2+c2-2 bccos. (2)平行四边形成为菱形的充要条件是对角线互相垂直: (3)内接于半圆且以直径为一边的三角形为直角三角形: (4)三角形各边的垂直平分线共点月这点到各项点等距 (⑤)空间四边形对角线五相垂直的充要条件是对边半方和相等 证明:(1)如图1-21,△4BC中,设c=b,c=c,BC=a, .al=a,b|=b.c=c.a=b-c, 图1-11 a2=(i-cy2=62+c2-26.c=62+c2-26 llclcos4. 此即 a=b2+c2-2bccosA. (4)图1-22,设AB,BC边的垂直平分线PD,PE相交于P D,E,F为AB,BC,CA的中点,设PA=a,PB=b,PC=c, 则丽=万-a.死=-6,ā=8-,m=a-6 PE=(c+B). 因为PD⊥AB,PE⊥BC 所以 a-6x6-a)-=62-a-0 6-xc-i)=c-6=0 从而有a2=62=c2,即1aP=16=|c2, 图1-12 所以 5c+aa-8)a-e-0 所以PF⊥CA, 月1al=|b1=|cL 故三角形各边的垂直平分线共点月这点到各顶点等距. §1.8两向量的失性积 1.证明(a×b)2≤a2.62,并说明在什么情形下等号成立. [证明]:(a×b)2=|axbP=|a16sin2∠(a,b) aP bP=a2.62. 要使等号成立,必须sin2∠(a,b)=1,从而sin∠(a,b)=1, 故∠(a,6)=,即当a16时,等号成立 2 2.证明如果a+b+c=0,那么a×b=b×c=c×a,并说明它的几何意义. [证明]:山a+b+c=0,有(a+b+c)×c=0×c=0,但c×c=0, 于是a×c+b×c=0, 所以b×c=c×a. 同理山(a+b+c)×a=0,有c×a=a×b, 从而a×b=b×c=c×a

其几何意义是以三角形的任二边为邻边构成的平行四边形的面积相等. 3.如果非零向量=1,2,3)满足广=万×万,万=万×开,=万×,那么,2,乃是彼此 垂直的单位向量,并月按这次序构成右手系. [证明]:山矢性积的定义易知,5,彼此垂直,月构成右手系。 下证它们均为单位向量 因为 万=万x5,万=万x行, 所以=万店5k。=万I山 所以= 山于150,从而152=1,15=1. 同理可证15=1,5=1 从而万,5,5都是单位向量。 图1-13 4.用向量方法证明: (1)三角形的正弦定理 b C sinA sin B sinC (2)三角形面积的海伦Heron)公式,即三斜求积公式: △2=pp-ap-b)p-c). 式中p=)a+6d是三角形的半周长,△为三角形的面积 [证明]:()如图1-13,在△4BC中,设BC=a,C=b,AB=c, al=a,1B=b,Ic|=c,a+b+c=0. 从而有b×c=c×a=a×b, 所以lb×cl=|c×a|=|a×b, bcsinA=casinB=absinC, 于是 b sinA sin B sinC (2)同上题图,△ABC的面积为 所以 A=I(ax6Y. 4 因为 (a×b)2+(a-b)2=a262 所以 4-4a6-(a61 山于 a+6+c=0, 从而 a+6=-c,(a+6)2=c2 所以 a6=e-a-6-e2-i-6 故有 a2=a62-1e2-a2-b的 =Ga-e-d-2ab1e2-f-】

=Go6-Ic-o-6的 =I(a-b+e)(a-b-cH(e+a-bXc-a+b) 16 =62p2p-202p-2b2p-20 所以△2=p0p-a)0p-bp-c 或△=Vp(p-a)p-b(p-c) §1.9三向量的混合积 L.设a,i,c为三个非零向量,证明 (1)(a,B,c+aa+ub)=(a,B,c); (2)(a+b,b+c,c+a)=2(a,b,c). [证明]:(1)左端=(a×b)(c+入a+ub) =(a×bc+(axb)(0a)(a×b)(ub) =(a×b)yc+(a×b)a+u(a×b)b =(abc)th(ab a)tu(abb) =(a6c)=右端. (2)左端=[(i+c)x(c+a)](a+i) =[b×c+b×a+c×a](a+b) -(Bxc)a+(Bxa)a+(cxa)a+(Bxc)B+(Bxa)B+(cxa)b =(石ca)-(cai)2(a6c)右端. 2.设径矢0A=斤,OB=2,0C=乃,证明R=(G×)十(5×)十(G×) 垂直于ABC平面. [证明]:由于AB.R=(,-r)[(G×5)+(×5)+(G×)] =(555)+(555)+(55)-(G5)-(G55)-(G5) =(5)-(G535)=0, 所以AB⊥R」 同理可证ACLR. 所以R⊥平面ABC 3.i=ae +be,+ce,,i=ae +be,+ce,,w=ae,+be,+ces, a b c 试证明 (i,v,w)a:b:c(eees). a3 b3 Cs [证明]:a×= a(exe) ca (e,xe;) az b (e,×e2)+ b,c. C,a, ∴.(i,卫,w)=(a×)币