
3.2定积分 3.2.1两个实例 3.2.2定积分的概念 3.2.3定积分的性质 3.2.4微积分基本定理 3.2.5定积分的换元积分法和分部积分法 3.2.6广义积分
3.2 定积分 3.2.1 两个实例 3.2.2 定积分的概念 3.2.3 定积分的性质 3.2.4 微积分基本定理 3.2.5 定积分的换元积分法和分部积分法 3.2.6 广义积分
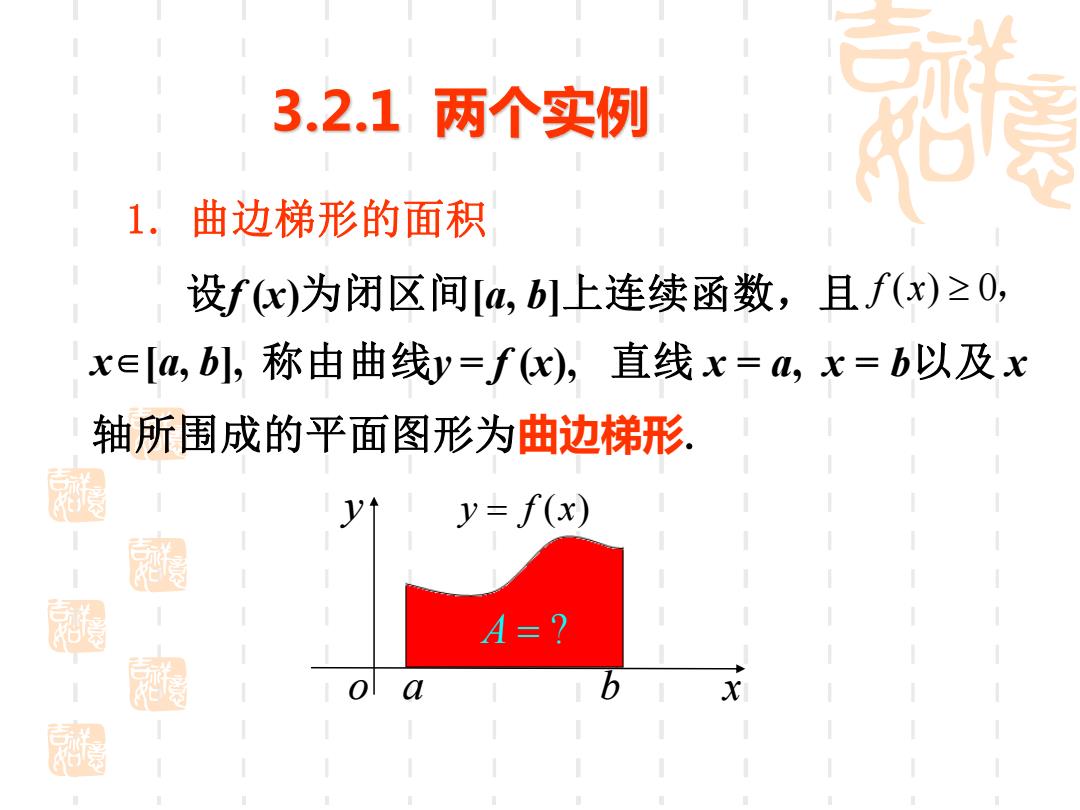
3.2.1两个实例 1.曲边梯形的面积 设fx)为闭区间[4,b上连续函数,且f(x)≥0, x∈[a,b,称由曲线y=fx),直线x=a,x=b以及x 轴所围成的平面图形为曲边梯形, 湖 V y=f(x) A=? 0 a X
o x y y = f (x) a b 轴所围成的平面图形为曲边梯形. 设f (x)为闭区间[a, b]上连续函数,且 f x( ) 0 , x∈[a, b], 称由曲线y = f (x), 直线 x = a, x = b以及 x 1. 曲边梯形的面积 3.2.1 两个实例 A = ?
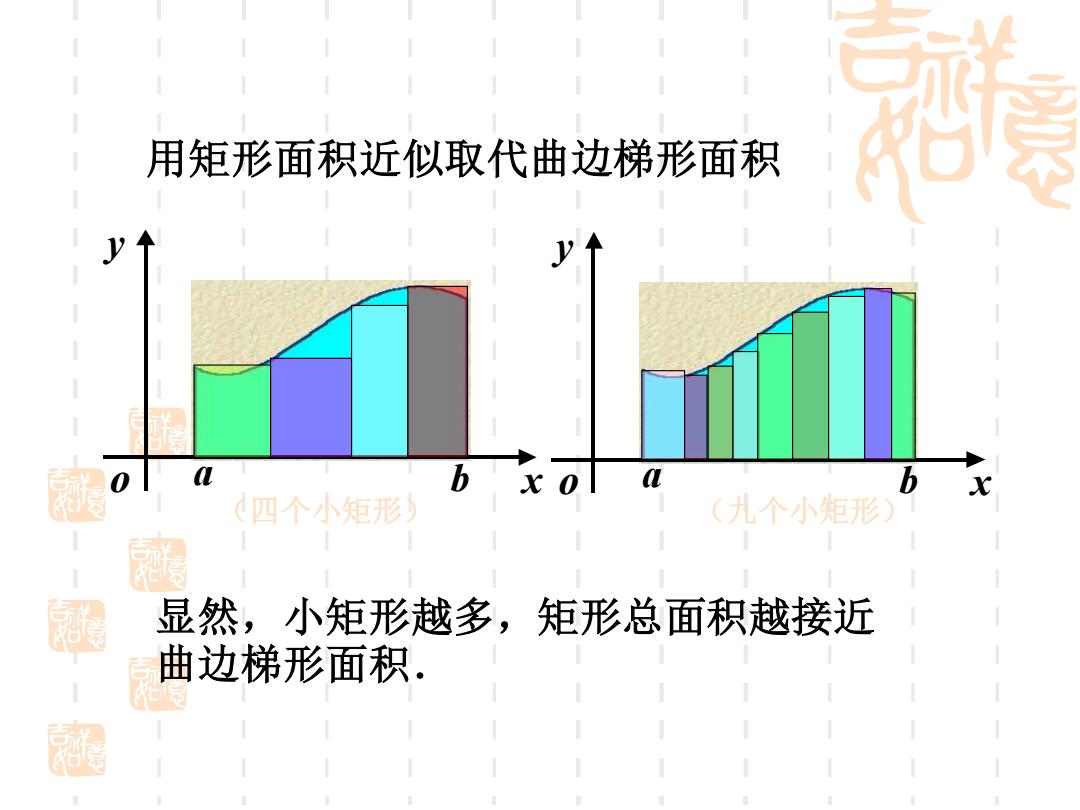
用矩形面积近似取代曲边梯形面积 0 L b 四个小矩形) (九个小矩形 显然,小矩形越多,矩形总面积越接近 曲边梯形面积
a b x y a b x o y o 用矩形面积近似取代曲边梯形面积 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. (四个小矩形) (九个小矩形)
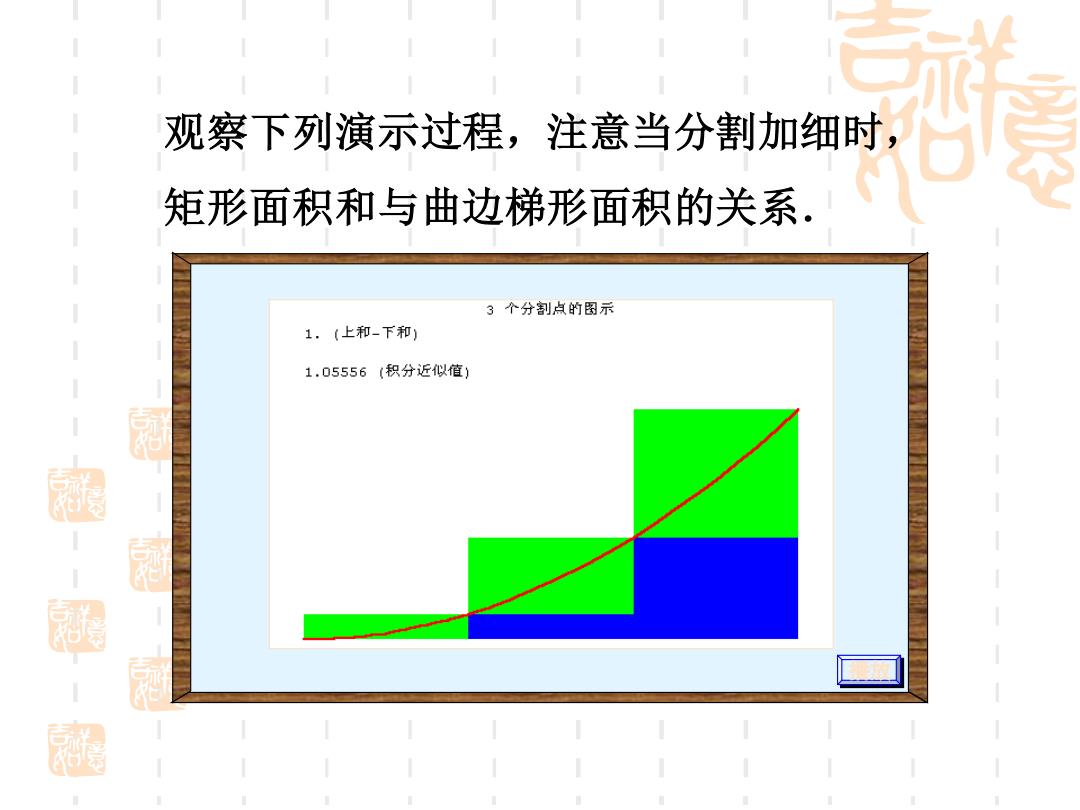
观察下列演示过程,注意当分割加细时 矩形面积和与曲边梯形面积的关系. 3个分割点的图示 1.(上和-下和) 1.05556(积分近似值) 极紅私
观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系. 播放
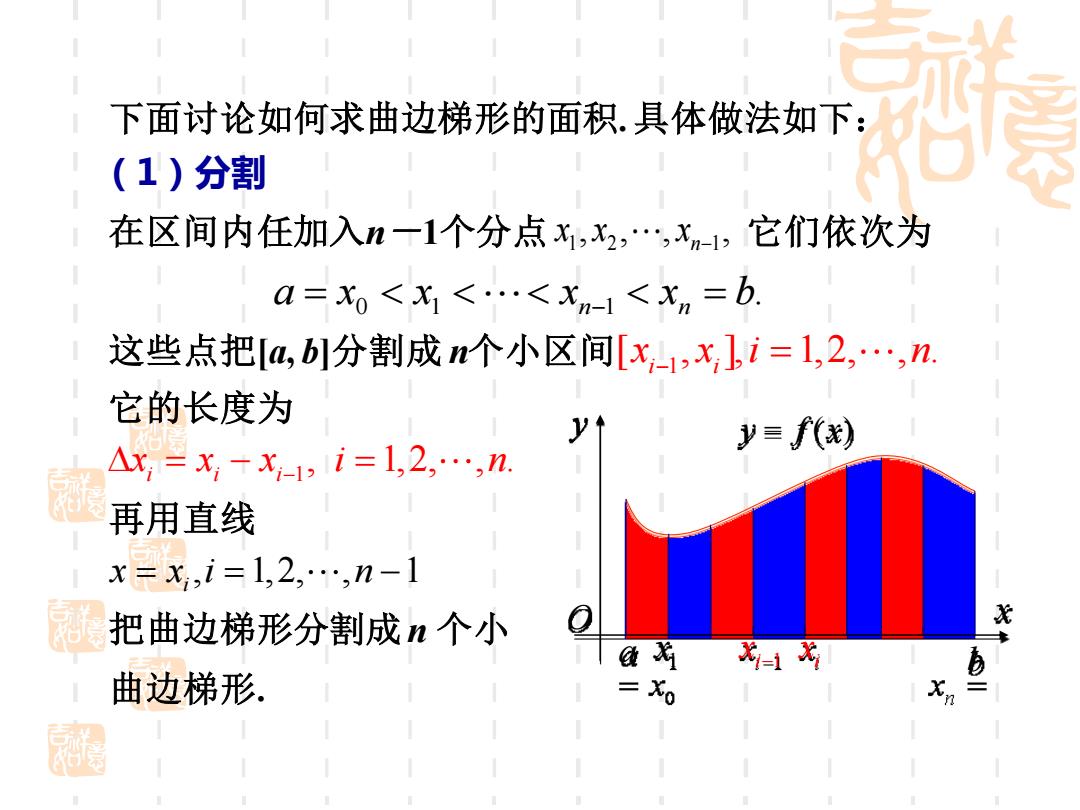
下面讨论如何求曲边梯形的面积.具体做法如下:。 (1)分割 在区间内任加入n一1个分点x,x2,,xm-,它们依次为 a=xo<x<..<Xn-1<X=b. 这些点把[a,b]分割成个小区间[x1,x,]i=1,2,…,n, 它的长度为 y三f() Ax,=x-X12i=1,2,…,n. 再用直线 x=x,i=1,2,…,n-1 把曲边梯形分割成n个小 位 11为 曲边梯形. 三0
. a = x0 x1 xn−1 xn = b 下面讨论如何求曲边梯形的面积. 具体做法如下: (1)分割 这些点把[a, b]分割成 n个小区间 1 [ , ], 1,2, , . i i x x i n − = 它的长度为 1 , 1,2, , . i i i x x x i n = − = − 再用直线 , 1,2, , 1 i x x i n = = − 把曲边梯形分割成n 个小 在区间内任加入n-1个分点 它们依次为 y = f (x) x y O a 1 b x i 1 x − i x 曲边梯形. , , , , 1 2 n−1 x x x
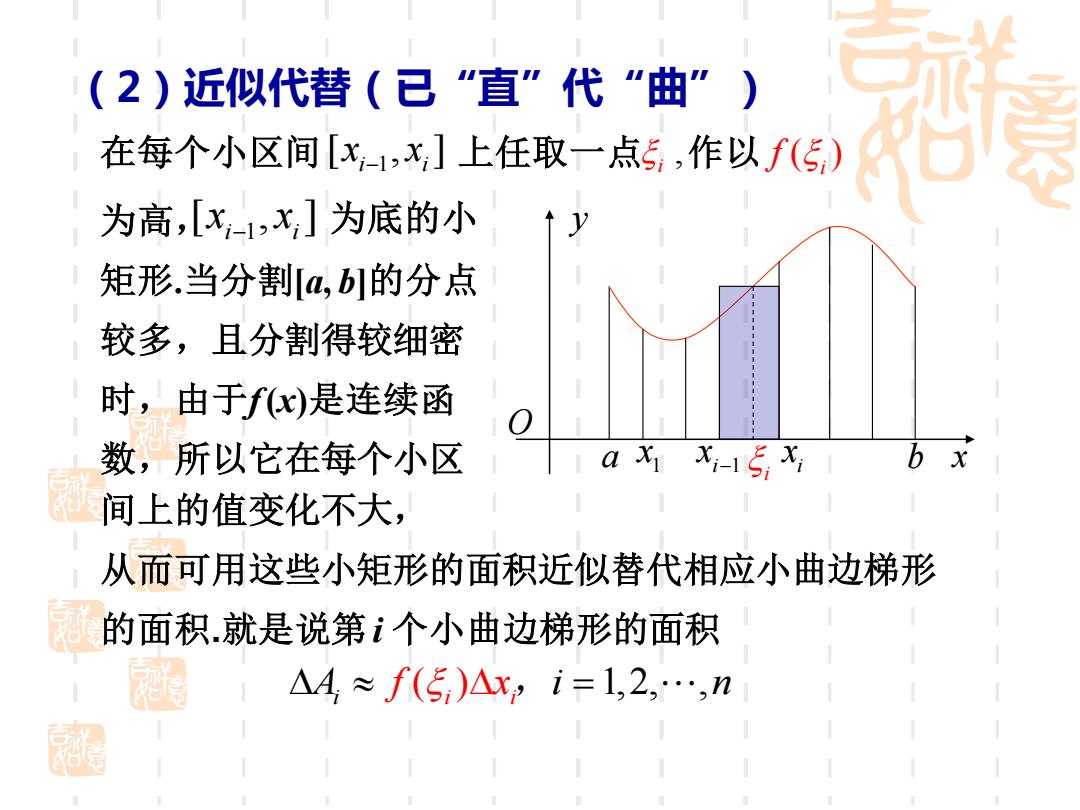
(2)近似代替(已“直”代“曲”) 在每个小区间[x-1,x]上任取一点5,作以f(5) 为高,[x1,x]为底的小 矩形.当分割4,b]的分点 较多,且分割得较细密 时,由于fx)是连续函 数,所以它在每个小区 ax1x-1x 间上的值变化不大, 从而可用这些小矩形的面积近似替代相应小曲边梯形 的面积就是说第i个小曲边梯形的面积 △4≈f(5)Axi=1,2,…,n
(2)近似代替(已“直”代“曲”) 在每个小区间 1 [ , ] i i x x − 上任取一点 , i 作以 ( )i f 为高, 1 [ , ] i i x x − 为底的小 矩形.当分割[a, b]的分点 较多,且分割得较细密 时,由于f (x)是连续函 数,所以它在每个小区 间上的值变化不大, 从而可用这些小矩形的面积近似替代相应小曲边梯形 的面积.就是说第i 个小曲边梯形的面积 ( ) 1,2, , i i i = A i n f x , x y O a x1 xi−1 xi b i
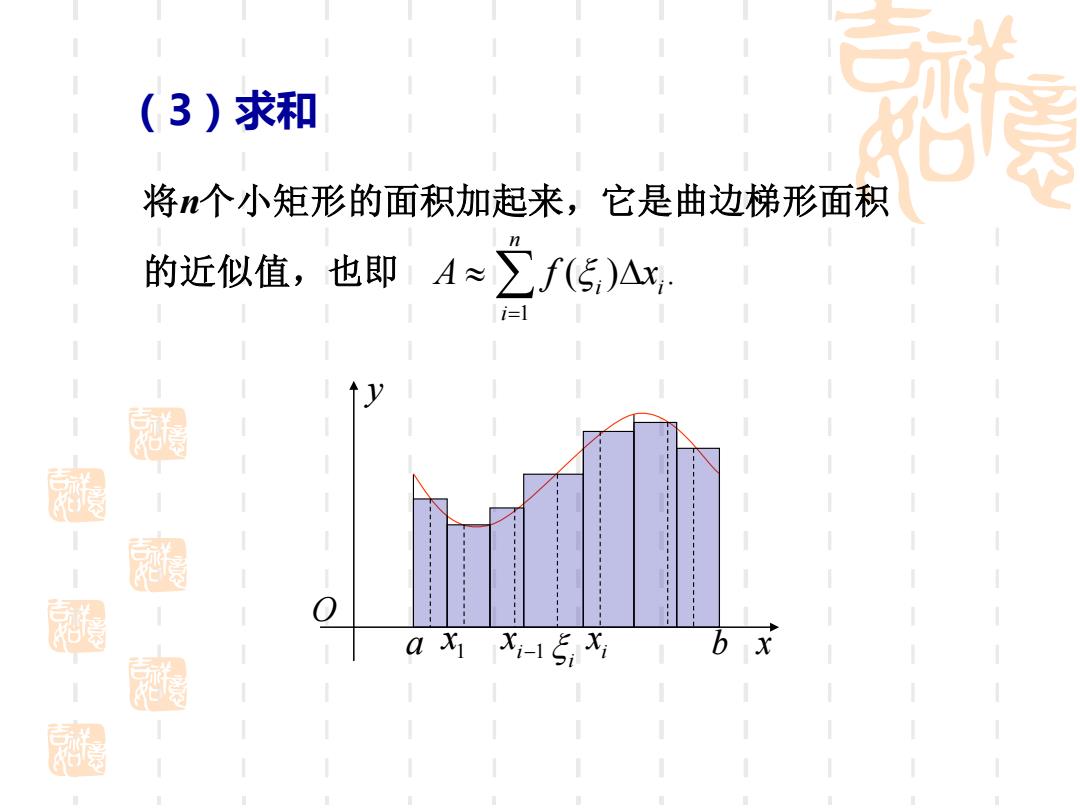
(3)求和 将个小矩形的面积加起来,它是曲边梯形面积 的近似值,也即A≈∑f(5)△x ax xi-1x X
1 ( ) . n i i i A f x = (3)求和 将n个小矩形的面积加起来,它是曲边梯形面积 的近似值,也即 x y O a x1 xi−1 xi b i

(4)取极限 显然,∑f(5,)△x,与区间[a,1的分割方法有关, i=1 也与5的选取有关.但是可以想象,当分点无限增 多,且对[,b无限细分时,如果此和式与某一常数 无限接近,且与分点x,以及点5的选取无关时, 则此常数应该是该曲边梯形的面积.令 元=max{Ax,Ax2,…△xn} 则 曲边梯形面积为 A=lim∑f(5,)Ax 1→0 i=l
多,且对[a, b]无限细分时,如果此和式与某一常数 (4)取极限 显然, 1 ( ) n i i i f x = 与区间[a, b]的分割方法有关, 也与 i 的选取有关. 但是可以想象,当分点无限增 无限接近,且与分点 i x 以及点 的选取无关时, 则此常数应该是该曲边梯形的面积. 令 = max{ , , } x x x 1 2 n 则 0 1 lim ( ) n i i i A f x → = = 曲边梯形面积为 i
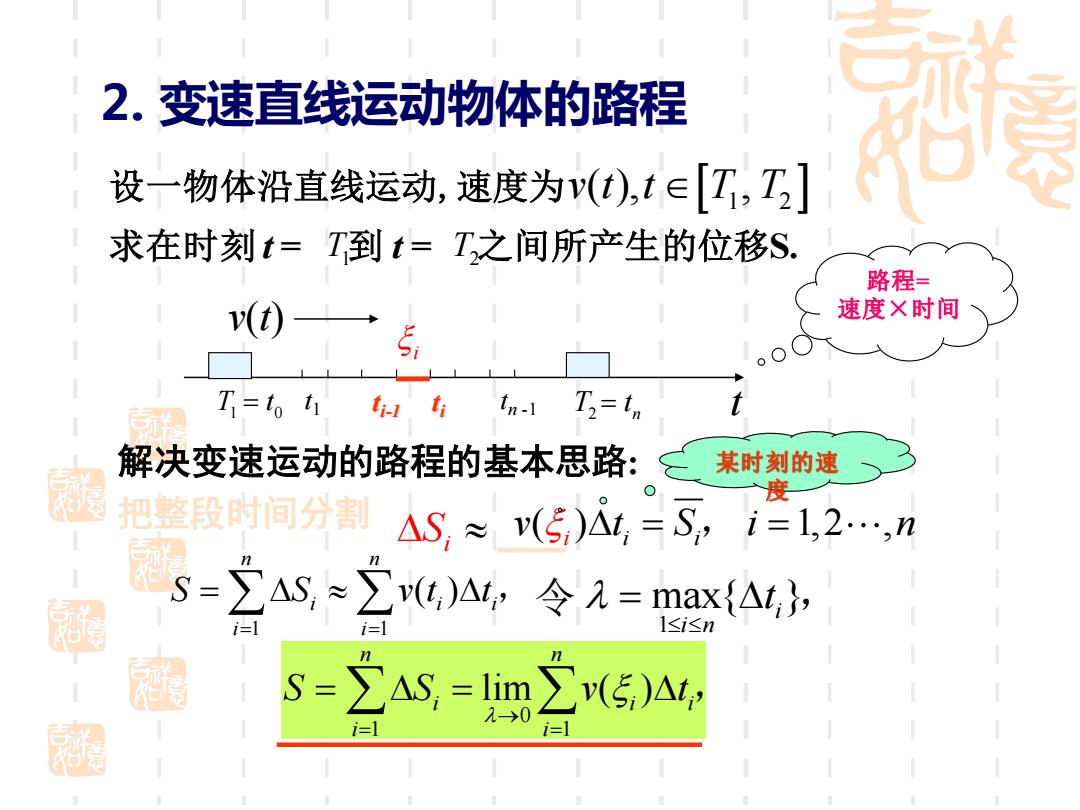
2.变速直线运动物体的路程 设一物体沿直线运动,速度为v(t),t∈[T,T,] 求在时刻t=T到t=T,之间所产生的位移S. 路程= v(t) 速度X时间 T=to t1 ti-l ti In-1 T=tn 解决变速运动的路程的基本思路: 某时刻的速 把整段时间分割 度 △S≈(5),=S,i=1,2…,n S=∑AS,≈∑t,)A,令=max{△t, i=1 S=∑AS,=lim∑(5)At;
2. 变速直线运动物体的路程 v t t T T ( ), , 1 2 ( ) 1,2 , i i i v t S i n = = , 设一物体沿直线运动,速度为 解决变速运动的路程的基本思路: 把整段时间分割 0 = t t t1 ti tn -1 v(t) n = t T1 T2 求在时刻 T2 t = 到 t = 之间所产生的位移S. T1 i S 路程= 速度×时间 , = = = n i i i n i i S S v t t 1 1 ( ) 1 max{ }i i n t 令 = , 0 1 1 lim ( ) n n i i i i i S S v t → = = = = , ti-1 i 某时刻的速 度

A=lim∑f(5)△x, 20=1 S=lim∑v(5,)△t, →0 i=1 (1)分割 (2)近似替代 (3)求和 (4)取极限
i n i A = f i x = → lim ( ) 1 0 0 1 lim ( ) n i i i S v t → = = (1)分割 (3)求和 (4)取极限 (2)近似替代