
2.3中值定理与导数的应用 2.3.1拉格朗日(Lagrange)中值定理 2.3.2洛必塔法则 2.3.3函数的单调性和极值 2.3.4函数的最大值与最小值 涵 2.3.5函数曲线的凹凸性与拐点 2.3.6函数曲线的渐近线 酒 2.3.7函数图形的描绘
2.3 中值定理与导数的应用 2.3.1 拉格朗日(Lagrange)中值定理 2.3.2 洛必塔法则 2.3.3 函数的单调性和极值 2.3.5 函数曲线的凹凸性与拐点 2.3.7 函数图形的描绘 2.3.6 函数曲线的渐近线 2.3.4 函数的最大值与最小值

2.3.1拉格朗日(Lagrange)中值定理 定理2-7(罗尔(Roe)定理) 若f(x)满足: (1)在a,b]上连续, (2)在(4,b)内可导, (3)f(0=f(b), 湖 则至少存在一点衫∈(a,b),使得f'(5)=0
定理2-7(罗尔(Rolle)定理) 若 f (x)满足: (1)在[a, b]上连续, (2)在(a, b)内可导, (3)f (a) = f (b), 则至少存在一点 ( , ) a b , 使得 f ( ) 0. = 2.3.1 拉格朗日(Lagrange)中值定理
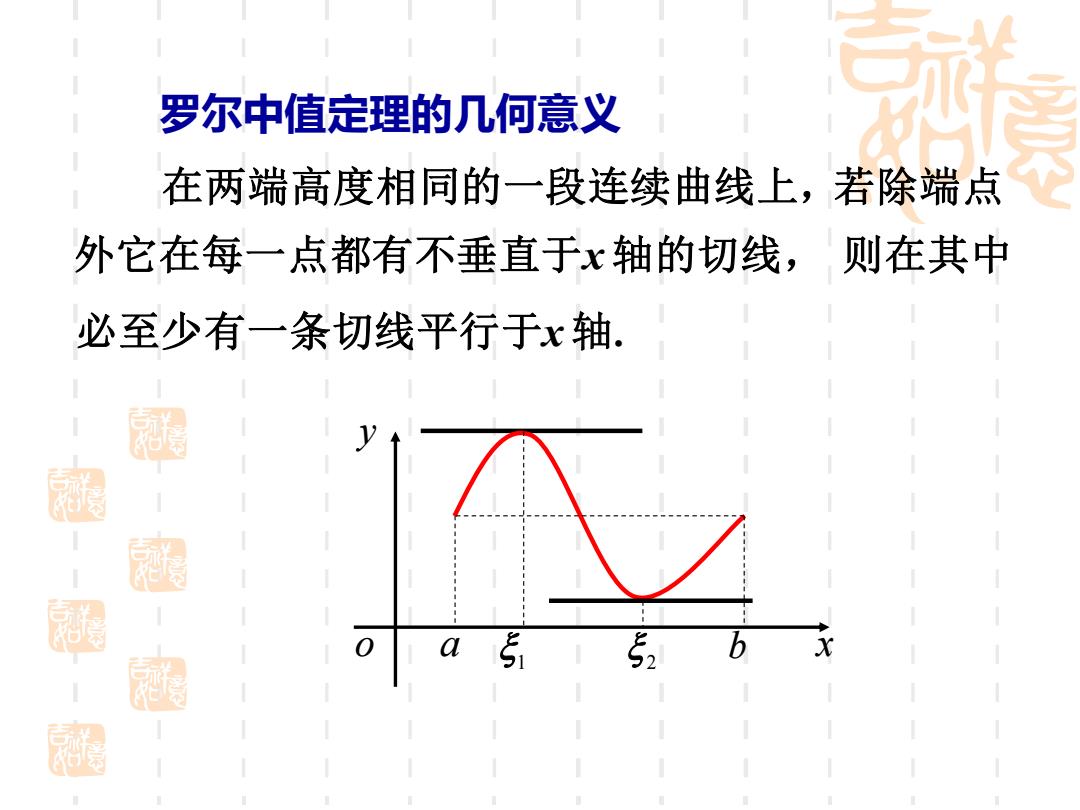
罗尔中值定理的几何意义 在两端高度相同的一段连续曲线上,若除端点 外它在每一点都有不垂直于x轴的切线,则在其中 必至少有一条切线平行于x轴. 51 b
罗尔中值定理的几何意义 o x y a b 1 2 在两端高度相同的一段连续曲线上,若除端点 外它在每一点都有不垂直于x 轴的切线, 则在其中 必至少有一条切线平行于x 轴

耐 定理2-8(拉格朗日(Lagrange)中值定理 (1) 如果函数fx)在闭区间4,b]上连续, 在开区间 (a,b)内可导,那么在(a,b)内至少有一点飞(a<<b), 使等式 f(b)-f(a=f'(5)b-a)成立 拉氏公式 结论亦可写成fb-f@='传 b-a
如果函数 f(x)在闭区间[a,b]上连续, 在开区间 (a,b)内可导,那么在(a,b)内至少有一点(a b), 使等式 f b f a f b a ( ) ( ) ( )( ) − = − 成立. (1) (2) ( ). ( ) ( ) = − − f b a f b f a 结论亦可写成 定理2-8(拉格朗日(Lagrange)中值定理) 拉氏公式
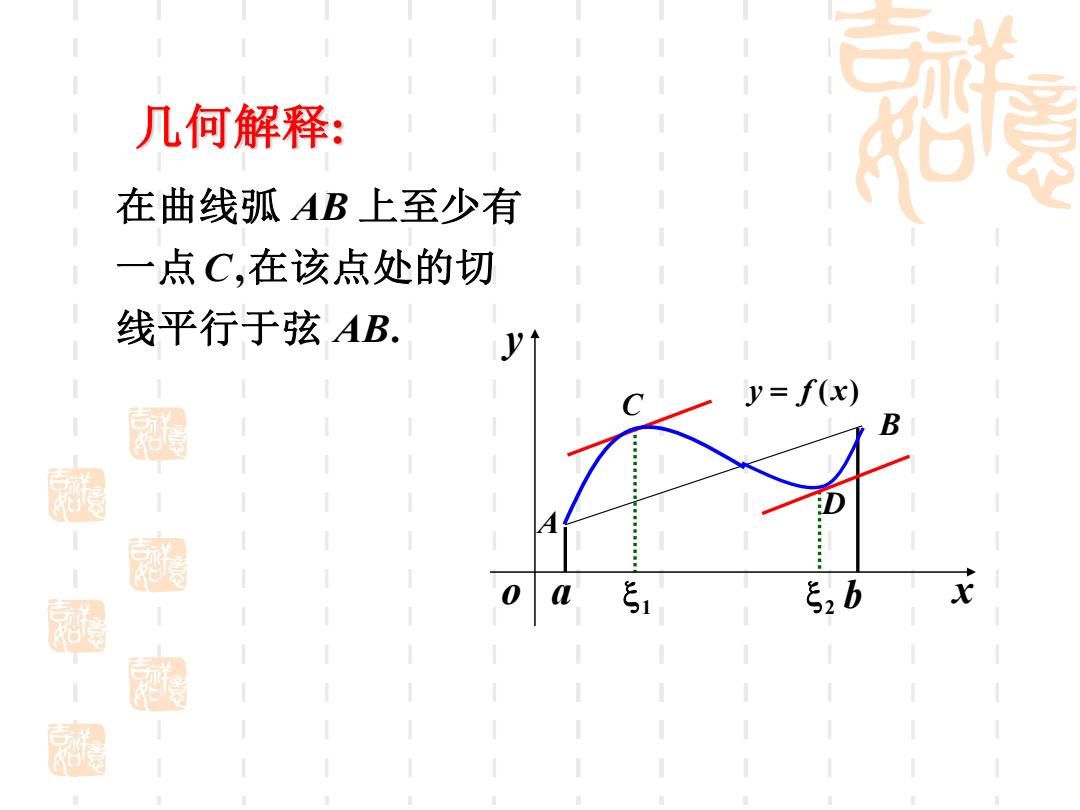
几何解释: 在曲线弧AB上至少有 一点C,在该点处的切 线平行于弦AB. y y=f(x) 涵 51 52b X
o a 1 2 b x y y = f (x) A B C D 几何解释: . , AB C AB 线平行于弦 一点 在该点处的切 在曲线弧 上至少有

!注 若fx)在a,b]上满足拉格朗日中值定理的条 件,则当f()=fb)时, 即得出罗尔中值定理的结 论.因此,罗尔中值定理是拉格朗日中值定理的 湿 一个特殊情形. 极腿
注 论. 因此,罗尔中值定理是拉格朗日中值定理的 一个特殊情形. 若f (x)在[a, b]上满足拉格朗日中值定理的条 件,则当f (a)=f (b)时,即得出罗尔中值定理的结

注意:拉氏公式精确地表达了函数在一个区间上的 增量与函数在这区间内某点处的导数之间的关系 推论1 如果对于任意x∈(a,b), 有f'(x)=0,则f(x)=c(c为常数) 推论2 如果对于任意x∈(a,b) 有f'(x)=g'(x),则f(x)=g(x)+c(c为常数) 井
推论1 推论2 ( , ) ( ) ( ) ( ) ( ) ( x a b f x g x f x g x c c = = + 如果对于任意 有 , 则 为常数) ( , ), ( ) 0 ( ) ( ) x a b f x f x c c = = 如果对于任意 有 , 则 为常数 注意: 拉氏公式精确地表达了函数在一个区间上的 增量与函数在这区间内某点处的导数之间的关系. #

2.3.2洛必塔法则 定义如果当x→a(或x→oo)时,两个函数f(x) 与g(x)都趋于零或都趋于无穷大,那末极限 im 称为或°型未定式(或不定式) x-→a. 0 00 (x→0) g(x) 例如, tanx In sin ax lim lim x-→0 0 Insin bx 本节将以导数为工具,给出计算未定式极限的一般方 凝 法,即洛比塔(L'Hospital)法则
定义 ( ) ( ) ( ) , ( ) ( ) , ( ) 0 lim . x a ( ) 0 x x a x f x g x f x → g x → → → 如果当 或 时 两个函数 与 都趋于零或都趋于无穷大 那 未定式 末极限 称为 或 型 或不定式 例如, , tan lim 0 x x x→ , lnsin lnsin lim 0 bx ax x→ 0 0 2.3.2 洛必塔法则 本节将以导数为工具,给出计算未定式极限的一般方 法,即洛比塔(L’Hospital)法则

定理2-9(洛必塔法则)设f(x),g(x)满足 ()当x→x,时,函数f(x)及g(x)都趋于零; (2)在点x,的某领域内(点x,本身可以除外), f'(x)及g(x)都存在且g'(x)≠0; (3)lim f'(x) 存在(或为无穷大); x→X0 g'(x) 型 0 则lim f(x) ≥i f'(x) x→X0 8(x) →x0 g'(x) 型 注1:当x→∞时,该法则仍然成立 注2:当f(x)及g(x)都趋于无穷大时 该法则仍然成立
0 0 0 0 0 0 (1) ( ) ( ) (2) ( ) ( ) ( ) 0; ( ) (3) lim ( ) ( ) ( ) lim lim . ( ) ( ) 当 及 在点 及 都存在且 x x x x x x x x f x g x x x f x g x g x f x g x f x f x g x g x → → → → = = 函数 零 则 时, 都趋于 ; 的某领域内(点 本身可以除外), 存在(或为无穷大); 定理2-9(洛必塔法则)设 满足 ( ) ( ) x f x g x 注1:当 →∞时,该法则仍然成立. 当 及 都趋于无穷大时, 该法则 注2: 仍然成立. f (x), g(x) 型 0 0 型

tanx 少例1 求lim量 x→0 〔8 解 原式=lim tanx)' sec"x lim =1. x→0 () x→0 1 少例2求lim x3-3x+2 i四x-x2-x+1 超 3x2-3 解原式=lim 6x 3 lim x13x2-2x-1-16x-2 2 蘭
例 1 解 . tan lim0 x x x → 求 0 (tan ) lim ( ) x x → x 1 sec lim 2 0 x x → = = 1 . 例 2 解 . 1 3 2 lim 3 2 3 1 − − + − + → x x x x x x 求 2 2 1 3 3 limx 3 2 1 x → x x− − − 6 2 6 lim1 − = → x x x . 23 = 00 00 原式 = 原式 =