
6.3可降阶的二阶微分方程 二阶及二阶以上的微分方程称为高阶微分方程: 高阶微分方程没有一般的求解方法,只有几种特 殊类型的可找到求解途径. 本节介绍三种容易降阶的高阶微分方程的求解方法: 6.3.1Jym=f)型 晟秋私 6.3.2y”=f化,y)型 极起 6.3.3y"=f0y,y)型
6. 3 .1 y (n) = f (x) 型 6. 3 .2 y = f (x, y) 型 6. 3 .3 y = f (y, y) 型 二阶及二阶以上的微分方程称为高阶微分方程. 高阶微分方程没有一般的求解方法,只有几种特 殊类型的可找到求解途径. 本节介绍三种容易降阶的高阶微分方程的求解方法. 6.3 可降阶的二阶微分方程

6.3.1m=fx)型 1.特点右端仅含有自变量x. 2.解法积分n次即可得通解 y=∫f(x)dc+C dy》=[f(x)+C]+C 凝 dy=∫[jf(x)+C+C]a+C
2. 解法 1. 特点 右端仅含有自变量 x . 积分 n 次即可得通解 . 1 ( 1) y f ( x ) dx C n = + − ( 2) 1 2 ( ) n y f x dx C dx C − = + + 1 2 ( ) . n y f x dx C dx C dx C = + + + 6. 3 .1 y (n) = f (x) 型

之例1解微分方程 2y四=0,y=1y"4)=2. Inx ”小== 解 c_1+C, 代入y"(1)=2, 得出C1=3. -- 极秋秘 =3x-Im'x-Imx+Cz 2
例1 解微分方程 解 代入 y(1) = 2, , (1) 0, (1) 1, (1) 2. ln 2 = y = y = y = x x y = = dx x x y y dx 2 ln , ln 1 C1 x x x = − − + = − − dx x x ln x 1 3 y = y dx ln ln , 2 1 3 2 2 = x − x − x + C 得出 C1 = 3

y-jy'd-3x-'x-lax+C 2 代入y'()=1, 得出C2=-2. y-J(3x-2lnx-Inx-2)db 3x-2x-x+C3 2 涵 代入y(①)=0,得出C,=2 所求特解 一 y=-2x-nx+月
y = y dx ln ln , 2 1 3 2 2 = x − x − x + C 代入 y(1) = 1, 代入 y (1) = 0, 得出 C3 = 所求特解 得出 C2 = −2. y = x − ln x − ln x − 2)dx 2 1 (3 2 ln , 2 2 2 3 3 2 2 x C x = x − x − + 2 1 . 2 1 ln 2 2 2 3 2 2 = − − x + x y x x
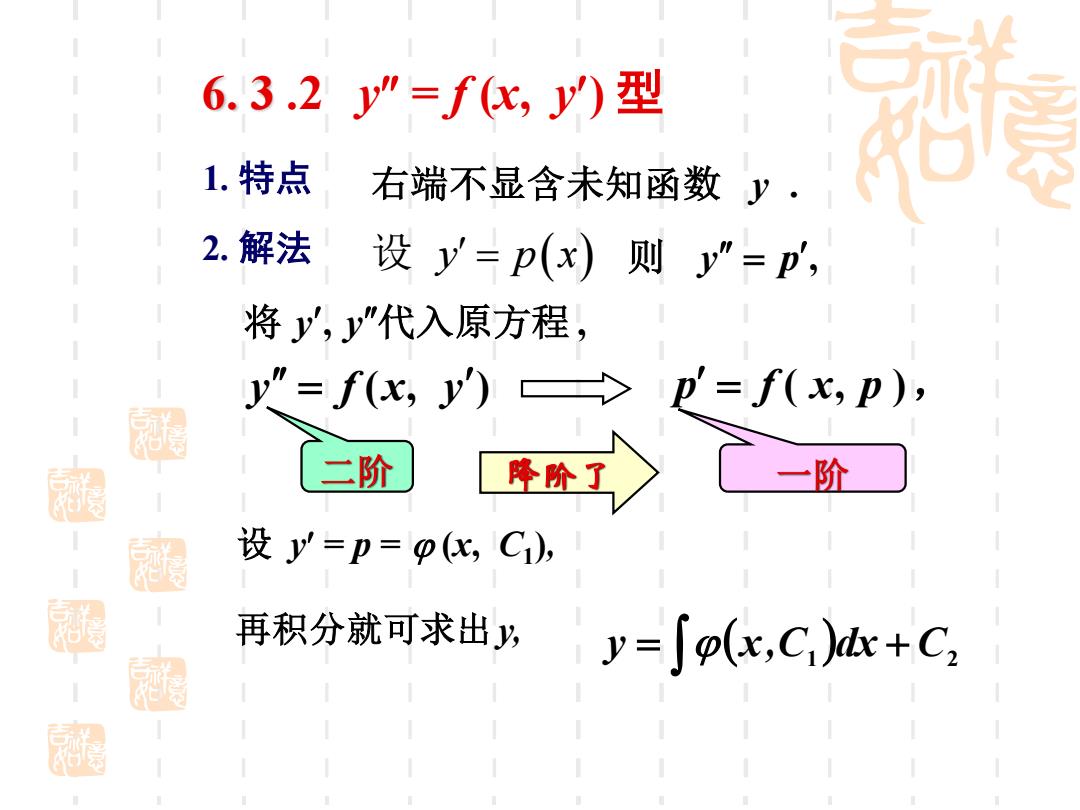
6.3.2y”=f化,y)型 1.特点 右端不显含未知函数y 2.解法 设y=p(x)则y”=p', 将y,y”代入原方程 y"=f(x,y'>p'=f(x,p), 二阶 降阶了 C一阶 -秋私 藏 设y'=p=p(,C1, 再积分就可求出gy=∫p(x,C)+C
设 y p x = ( ) 则 y = p , 1. 特点 右端不显含未知函数 y . 2. 解法 y = f (x, y ) p = f ( x, p ), 二阶 降阶了 一阶 设 y = p = (x, C1 ), 再积分就可求出 y, 将 y , y 代入原方程 , ( ) = C1 dx + C2 y x, 6. 3 .2 y = f (x, y) 型

例2求微分方程(1+x2)y”=2y的通解 解设y=p(),则y"=业, 代入原方程得 =2xp, 分离变量得 d迎 2x 1+x2 涵 两端积分得 In p=In(1+x2)+C, 即 p=y'=C11+x2) (C1=±C), 再积分得y=∫C0+x=Cx+9x+C 3
(1 ) 2 . 求微分方程 + x 2 y = xy 的通解 解 , dx dp 设 y p x = ( ) , 则 y = 代入原方程得 (1 ) 2 , 2 x p dx dp + x = ln ln (1 ) , 2 p = + x + C 例 2 , 1 2 2 dx x x p dp + 分离变量得 = 两端积分得 (1 ) ( ), 1 2 即 p = y = C1 + x C = C 2 3 1 1 1 2 (1 ) . 3 C y C x dx C x x C = + = + + 再积分得
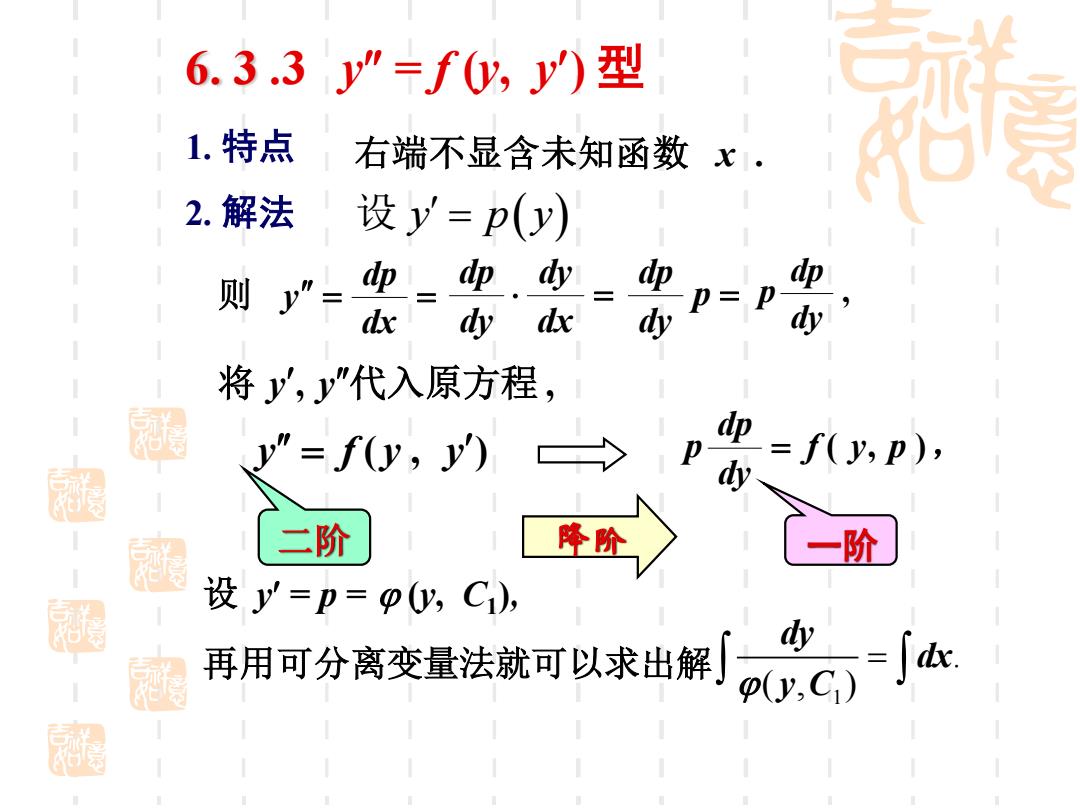
6.3.3y"=fy,y)型 1.特点 右端不显含未知函数x. 2.解法 设y=p(y) 则 dp dp dy dp dx dy dx y y 将y,y"代入原方程 y”=fy,y) =f(y,p), dy 二阶 降阶 一阶 设y=p=py,C), 再用可分离变量法就可以求出解 ca
设 y p y = ( ) = = dx dp 则 y 1. 特点 右端不显含未知函数 x . 2. 解法 y = f ( y , y ) f ( y, p ), dy dp p = 二阶 降阶 一阶 = dx dy dy dp p = dy dp , dy dp p 将 y , y 代入原方程 , 再用可分离变量法就可以求出解 1 . ( , ) dy dx y C = 设 y = p = (y, C1 ), 6. 3 .3 y = f (y, y) 型

少例3 求微分方程y”-y2=0的通解 解一右端不显含未知函数x, 设y=p则y”= - dp dx dy d 代入原方程得 yp .-p2=0. dy 利 当p≠0时,约去p并分离变量,得 dp dy 极秋私 两端积分得 In p=In y +InC
0 . 求微分方程 yy − y 2 = 的通解 解 一 0. 2 − p = dy dp y p 例 3 设 y = p = = dx dp 则 y 右端不显含未知函数 x , = dx dy dy dp , dy dp p 代入原方程得 当 p 0时,约去 p 并分离变量,得 , y dy p dp = 两端积分得 ln ln ln , p y C = +

aw sf-Cy入 两端积分得lnp=lny+lnC, 两端再分离变量得 少=Cdk y 两端再积分得 Iny=Cx+InC2, 西 于是 y=C,e.(C3=±C2) 涵 当p=0时,y为常数,包含在y=C3eCx中, -秋私 超 所以通解为y=C3eCx
两端积分得 1 3 3 2 . ( ) C x 于是 y C e C C = = p y C y1 即 = = 两端再积分得 两端再分离变量得 1 2 ln ln , y C x C = + 当 p = 0时, y 为常数, 包含在 中, C x y C e 1 = 3 所以通解为 . 1 3 C x y = C e ln ln ln , p y C = + 1 ( ) C C = 1 dy C dx y =

心例4求微分方程”+y2=0的通解 解一右端不显含未知函数x,可用前面介绍的降阶法. a 解二y+y=01→k00=0 →y'=C→ydy=Cd 技巧性较高, -y-G0 关键是配导 数的方程 从而通解为 y2=Cx+C
解二 1 yy = C 从而通解为 2 例 4 求微分方程 yy y + = 0 . 的通解 技巧性较高, 关键是配导 数的方程 2 yy y + = 0 ( ) 0 y d dx y = 1 ydy = C xd 2 1 2 1 2 = + y C x C2 1 2 1 2 y C x C = + 解一 右端不显含未知函数 x , 可用前面介绍的降阶法