
第4章柱面、锥面、旋转曲面与二次曲面 §4.1柱面 1、已知柱面的雅线为: (x-1)2+(y+3)2+(z-2)2=25 x+y-z+2=0 月(1)母线半行于x轴:(2)母线半行于直线x=y,z=C,试求这些柱面的方程。 解:(1)从方程 (x-1)2+(y+3)2+(z-2)2=25 x+y-z+2=0 中消去x,得到:(z-y-3)2+(y+3)2+(z-2)2=25 即:y2+22-Jz-6y-52-3=0 此即为要求的柱面方程。 (2)取准线上一点M(xo,yo,zo),过M。月平行于直线 x=y的直线方程为: 2=c x=xo+t xo =x-t y=yo+t → Yo=y-t Z=Z0 z0=2 而M。在准线上,所以 (x-1-1)2+(y-t+3)2+(2-2)2=25 x+y-z-2t+2=0 上式中消去1后得到:x2+y2+3z2-2xy-8x+8y-8z-26=0 此即为要求的柱面方程。 x=y2+z2 2、设柱面的准线为 ,母线垂直于准线所在的平面,求这柱面的方程。 x=2z 解:山题意知:母线平行于矢量1,0,一2} 任取准线上一点M,(xo,yo,zo),过M,的母线方程为: x=xo+1 Xo=x-t y=yo 2=z0-21 Zo=z+2t

而M。在准线上,所以: x-1=y2+(z+2t)2 x-t=2(z+2t) 消去1,得到:4x2+25y2+z2+4xz-20x-10z=0 此即为所求的方程。 3、求过二条平行直线x=y=z,x+1=y=z-1,与x-1=y+1=z-2的圆柱面方程。 解:过原点且垂直于已知二直线的平面为x+y+z=0:它与已知直线的交点为 0,0,0以仁山,0,山,行,-行,等,这三点所定的在平面x+y+z=0上的圆的圆心为 M515 21113 ,圆的方程为: 15 15 15 x+y+z=0 此即为欲求的圆柱面的准线。 又过推线上一点M,(化,,2),月方向为红,1,1的直线方程为: x=x+1 x=x-1 y=y+t yi=y-t (Z=z (Z =z-t 将此式代入准线方程,并消去t得到: 5(x2+y2+z2-xy-z-2x)+2x+11y-13z=0 此即为所求的圆柱面的方程。 4、已知柱面的准线为y0={x(),y(u),z()},母线的方向半行于矢量S={X,Y,Z}, 试证明柱面的矢量式参数方程与坐标式参数方程分别为: x=Y(u)+vS 与 x=x(u)+Xv y=v(u)+Yv z=z(u)+Zv 式中的u,v为参数。 证明:对柱面上任一点M(x,y,z),过M的母线与准线交于点M'(x(W),y(),z(),则

M'M=vS 即 OM-OM=vS 亦即 Y-Y(u)=vS,Y=Y(u)+vS 此即为柱面的矢量式参数方程。 又若将上述方程用分量表达,即: x,y,z=(u),y(u),z(u)+vX,Y,Z x=x(u)+Xv y=v(u)+Yv z=z(u)+Zv 此即为柱面的坐标式参数方程。 §4.2锥面 1、求顶点在原点,推线为x2一2z+1=0,y-z+1=0的锥面方程。 解:设为锥面上任一点M(x,y,z),过M与O的直线为: X-Y_Z x y Z 设其与准线交于(X。,Y。,Z。),即存在1,使X。=x1,Y。=t,Z。=z1,将它们代入准线 方程,并消去参数t,得: x2-2z(z-y)+(z-y)2=0 即:x2+y2-z2=0 此为所要求的锥面方程。 2、已知锥面的顶点为(3,-1,-2),准线为x2+y2-z2=1,x-y+z=0,试求它的方程。 解:设M(x,y,z)为要求的锥面上任一点,它与顶点的连线为: X-3Y+1Z+2 x-3y+1z+2 令它与准线交于(X。,Y。,Z。),即存在1,使

[X。=3+(x-3)t X。=-1+(y+)t Z。=-2+(z+2)t 将它们代入准线方程,并消去1得: 3.x2-5y2+7z2-6xy-2z+10xz-4x+4y-4z+4=0 此为要求的锥面方程。 3、求以二坐标轴为母线的圆锥面的方程。 解:(这甲仪求I、Ⅶ卦限内的圆锥面,其余类推) 圆锥的轴1与i,j,k等角,故1的方向数为1:1:1 .与1垂直的平面之一令为x+y+z=1 平面x+y+z=1在所求的锥面的交线为一圆,该圆上已知二点(1,0,0),(0,1,0),(0,0,1), 该圆的圆心为 33了,故该圆的方程为: ,111 x+y-2+2-马2 3 x+y+z=1 它即为要求圆锥面的准线。 对锥面上任一点M(x,y,z),过M与顶点O的母线为: X-Y-Z x V Z 令它与准线的交点为(X。,Y。,Z。),即存在t,使X。=xt,Y。=1,Z。=zt,将它们代入 准线方程,并消去1得: Xy+yz+zx=0 此即为要求的圆锥面的方程。 4、求项点为(1,2,4),轴与平面2x+2y+z=0垂直,月经过点(3,2,1)的圆锥面的方程。 解:轴线的方程为:x一=y-2-2-4 221 过点(3,2,1)月垂直于轴的Ψ面为: 2(x-3)+2(y-2)+(z-1)=0 即: 2x+2y+z-11=0

该¥面与轴的交点为只,20,3),它与6,2,)的距离为: 9’9’9 ++- 3 .要求圆锥面的准线为: ✉-号+0-9+-1g 9 2x+2y+z-11=0 对锥面上任一点M(x,y,z),过该点与顶点的母线为: X-1-Y-2-Z-4 x-1y-2z-4 令它与准线的交点为(X。,Y。,Z。),即存在t,使X。=1+(x-1)1,Y=2+(y-2)t, Z。=4+(z-4)1 将它们代入准线方程,并消去t得: 51x2+51y+12z2+104xy+52z+52zx-518x-516y-252z+1299=0 5、已知锥面的准线为Y(u)=x(),y(u),z(u)},顶点A决定的径矢为Y。=xo,yo,zo}, 试证明锥面的矢量式参数方程与坐标式参数方程分别为: y=vy(u)+(1-v)yo 与 x=vx(u)+(1-v)xo y=vy(u)+(I-v)yo z=z(W)+(1-)z0 式中,4,y为参数。 证明:对锥面上任一点M(x,y,z),令OM=y,它与顶点A的连线交准线于 M'=(x(u),y(w),z(u),即OM'=y(4)。 :AM∥AM,月AM≠0(项点不在准线上) .AM=vAM' 即 7-%=v0y(0-) 亦即 y=vy(u)+(I-v)Yo

此为锥面的矢量式参数方程。 若将矢量式参数方程用分量表示,即: {x,y,z}=v{x(u),y(u),z(u)}+(1-v){,o,zo} x=vx(u)+(1-v)xo y=vy(u)+(1-v)yo z=vz(u)+(1-v)zo 此为锥面的坐标式参数方程,4,y为参数。 §4.3旋转曲面 1、求下列旋转曲面的方程: (1): x-1=y+1_2-1绕=上=一1旋转 1-12°1-12 (20: ==-绕==二旋转 21-11-12 (3) X一1-二=号绕2轴旋转: 1-33 2=x2 (4)空间曲线 绕z轴旋转。 x2+y2=1 解:()设M,(G,水,2)是母线一="+↓=二上任一点,过M的纬圆为: 1-12 (x-x)-(y-4)+2(z-z)=0 () x2+y2+(z-102=x2+2+(6-102 (2) 又M,在母线上。 -+1=名-1 1-12 从(1)一(3)消去,乃,乙,得到: 5x2+5y2+2z2+2y+4yz-4xz+4x-4y-4z-8=0 此为所求的旋转面方程。 (2)对母线上任一点M,(x,片,z),过M1的纬圆为: (x-x)-(y-y)+2(z-)=0 (①) 2+y2+(z-1)2=x2+y2+(a-1)2 (2)

因M在母线上, =业=3- (3) 21-1 从(1)—(3)消去x,,乙,得到: 5x2+5y2+23z2-12xy-24z+24xz-24x+24y-46z+23=0 此为所求的旋转面的方程。 (3)对母线上任一点M(x,y,z),过该点的纬圆为: z=Z (1) x2+y2+z2=x2+y2+z2 (2) 又M在母线上,所以: -1=五= (3) 1-33 从(1)—(3)消去x,,3,得到: 9(x2+y2)-10z2-6z-9=0 此为所求的旋转面方程。 (4)对母线上任一点M(x,,),过M1的纬圆为: z=21 (①) x2+y2+z2=x2+y2+z2 (2) 又M在母线上,所以 3=x2 (1) x2+2=1 (2) 从(1)一(3)消去,,,得到: x2+y2=1 z=Z1=x2≤1.0≤z≤1 即旋转面的方程为:x2+y2=1(0≤z≤1) 2、将直线士='一卫-绕z轴旋转,求这旋转面的方程,并就Q,B可能的值讨论这是什 a01 么曲面? 解:先求旋转面的方程式: 任取母线上一点M1(x,,),过M1的纬圆为:

2= (1) x2+y2+z2=2+y2+z2 (2) 又 ¥=乃-卫= (3) a0-1 从(1)—(3)消去x,,乙,得到: x2+y2-a2z2-B2=0 此即为所求旋转面的方程。 当a=0,B≠0时,旋转面为圆柱面(以z轴为轴): 当α≠0,阝=0时,旋转面为圆锥面(以z轴为轴,顶点在原点): 当a,阝≠0时,旋转面变为z轴: 当α=0,B≠0时,旋转面为单叶旋转双曲面。 3、已知曲线「的参数方程为x=x(u),y=y(u),z=z(),将曲线厂绕z轴旋转,求旋转曲 面的参数方程。 解:图,设M(x(W),y(),z(u)为T上任一点,则对经过M的纬圆上任一点p(x,y,z), 令p在xoy面上的射影为p' 令∠(i,0p)=0,则y=op=0p'+p'p M(x(),y(u),z(u) 而p=Vx2(0)+y2( 0 op=x2(u)+y2(u)cos0.+x(u)+y2(u)sin0.j p 而pp=z(u)k =x(u)+y(u)cos0+x(u)+y(u)sin0.j+z(u)k 此即为旋转面的矢量式参数方程,4,v为参数。 其坐标式参数方程为: x=/x2(u)+yi(u)cos0 y=x'(u)+y(u)sin0 (0≤0<2π) 2=z(u)
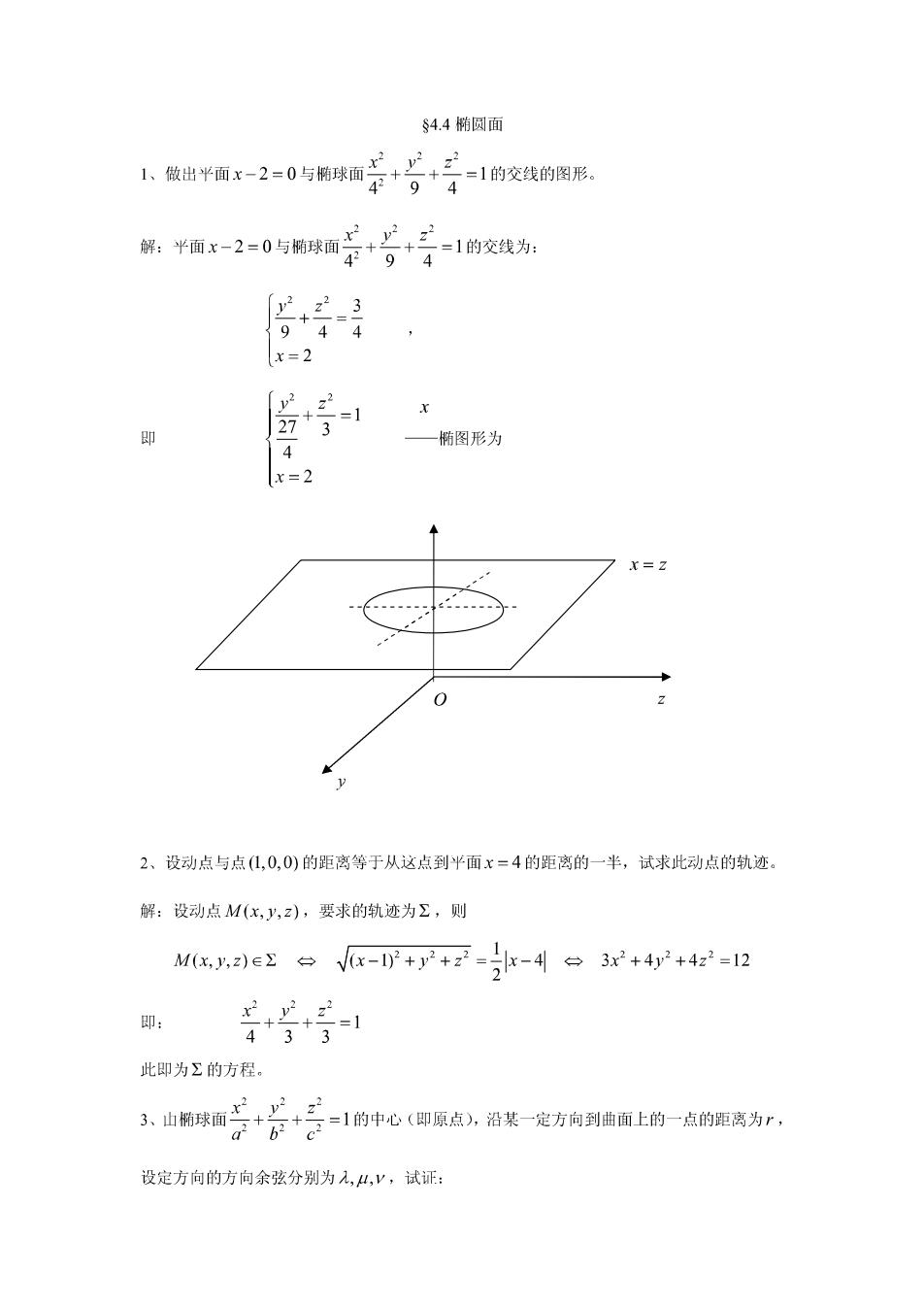
§4.4椭圆面 y2,z2 、做出半面x二2=0与椭球面+ =1的交线的图形。 94 解:半面x-2=0与椭球面。+广+ 4294 =1的交线为: 2 z23 944 9 x=2 y2 -=1 27 即 椭图形为 4 x=2 x=Z 0 物 2、设动点与点(L,0,0)的距离等于从这点到半面x=4的距离的一半,试求此动点的轨迹。 解:设动点M(x,y,z),要求的轨迹为∑,则 M(x,y,z)e∑= Vx-+产+2--4台3x+4+42=12 即: 4+3+3 =1 此即为Σ的方程。 3、由球面兰++三 a+6+ =1的中心(即原点),沿某一定方向到曲面上的一点的距离为r, 设定方向的方向余弦分别为入,4,V,试证:

1-2422 =+6+2 证明:沿定方向{,4,y到曲面上一点,该点的坐标为{r入,r4,rV 该点在曲面上见+心2w 即 12.2,v2 +6+ 、山椭球面子大 十+之=1的中心,引三条两两相五垂直的射线,分别交曲面A,P,2, 设叩,=,p,=5,p,=5,试证:↓+1+1=1+1+1 +疗+疗++园 2 .11242y2 证明:利用上题结果,有疗。+行+之 (i=1,2,3) 其中2,4,八是0p:的方向余弦。 若将op,(=1,2,3)所在的直线看成新的坐标系的二个坐标轴,则2,入2,入是坐标矢量关于 新坐标系的方向余弦,从而2+入2+2=1,同理,4,2+422+山2=1,y2+V22+y2=1 所以, 寻+诗0+似心*4 =1+11 即: 111111 ++疗++ 5、一直线分别交坐标面y0z,z0x,xoy于三点A,B,C,当直线变动时,直线上的三定点 A,B,C也分别在三个坐标面上变动,另外,直线上有第四点p,它与二点的距离分别为 α,b,c,当直线按照这样的规定(即保持A,B,C分别在二坐标面上)变动,试求p点的轨 迹。 解:设A0,y,3),B(x2,0,22),C(x3,3,0),则知: