
6.1微分方程的基本概念 6.1.1引例 6.1.2微分方程的基本概念 1.微分方程 2.微分方程的阶 3.线性微分方程 极秋秘 4.微分方程的解 5.微分方程的初始条件
6.1 微分方程的基本概念 6.1.1 引例 2.微分方程的阶 4.微分方程的解 6.1.2 微分方程的基本概念 1.微分方程 3.线性微分方程 5.微分方程的初始条件

6.1.1 引例 少例1一曲线通过点(1,2),且在该曲线上任一点M(x,y) 处的切线的斜率为2x,求这曲线的方程. 解 设所求曲线为y=y(x) 根据题意有 =2x dⅸ 这就是曲线y=f(x)所满足的微分方程 对其两端积分可得dy=2x→∫d=∫2xd →y=∫2xd所以y=x2+C, 当x=时,y=2 求得C=1, 所以,所求曲线为y=x2+1
例 1 一曲线通过点(1,2),且在该曲线上任一点M(x, y) 处的切线的斜率为2x,求这曲线的方程. 解 设所求曲线为 y = y(x) dy xdx = 2 当x =1时, y = 2 2 所以 y x C = + , 求得C =1, 2 所以,所求曲线为 y x = +1. x dx dy = 2 根据题意有 这就是曲线y=f (x)所满足的微分方程 对其两端积分可得 6.1.1 引例 = y xdx 2 = dy xdx 2

少例2质量为的物体,只受重力影响自由下落,试求 该物体下落的距离s应满足的微分方程. 解设物体自由下落的距离s和时间的关系为s=s④, 根据牛顿定律,所求未知函数s=s()应满足方程 d's 涵 dt2 =8 其中g为重力加速度
解 例2 质量为m的物体,只受重力影响自由下落,试求 该物体下落的距离 s 应满足的微分方程. 设物体自由下落的距离s和时间t的关系为s = s(t), 根据牛顿定律,所求未知函数s = s(t) 应满足方程 g dt d s = 2 2 其中g为重力加速度

例3通过临床观察,人们发现在肿瘤生长初期,肿 瘤细胞增长速度与当时该细胞数目成正比,比例系 数(相对增长率)为k,试建立该细胞数目在时刻 应满足的微分方程。 解设时刻t肿瘤细胞数目为n(t),根据题意可 以得到如下方程: n(t)=kn(t) y d's =2x 8 n'(t)=kn(t) d 以上三式都是含未知函数及其导数的关系式,统称 为微分方程
例3 通过临床观察,人们发现在肿瘤生长初期,肿 瘤细胞增长速度与当时该细胞数目成正比,比例系 数(相对增长率)为k ,试建立该细胞数目在时刻t 应满足的微分方程。 解 设时刻 t 肿瘤细胞数目为 n ( t ) ,根据题意可 以得到如下方程: n t k n t ( ) = ( ) 以上三式都是含未知函数及其导数的关系式,统称 为微分方程. x dx dy = 2 g dt d s = 2 2 n t k n t ( ) = ( )

6.1.2微分方程的基本概念 1.微分方程 凡含有未知函数的导数或微分的方程叫微分方程. 例 =2x d-s n()=kn() d y'=y, dt2 y"+2y'-3y=e*,(t2+x)dt+x=0, 实质】 联系自变量,未知函数以及未知函数的某 些导数(或微分)之间的关系式
凡含有未知函数的导数或微分的方程叫微分方程. 例 y = xy, ( ) 0, 2 2 3 , t + x dt + xdx = x y + y − y = e 实质 联系自变量,未知函数以及未知函数的某 些导数(或微分)之间的关系式. x dx dy = 2 6.1.2 微分方程的基本概念 1. 微分方程 g dt d s = 2 2 n t k n t ( ) = ( )

未知函数是一元函数的微分方程,称为常微分方程 未知函数是多元函数的微分方程,称为偏微分方程 例如 方程 dx +ax=t2是常微分方程, 方程 82T 82T 十 =0是偏微分方程 2 0z2 雨 注 本章只研究常微分方程,简称为微分方程 利 有时也简称为方程
注 未知函数是多元函数的微分方程,称为偏微分方程. 本章只研究常微分方程,简称为微分方程, 有时也简称为方程. 例如 d 2 d x ax t t 方程 + = 是常微分方程, 方程 2 2 2 2 2 2 0 T T T x y z ++= 是偏微分方程. 未知函数是一元函数的微分方程,称为常微分方程

2.微分方程的阶 微分方程中出现的未知函数导数的最高阶数 称为微分方程的阶. 阶微分方程F(x,,y=0,y'=f(x,y); 一 涵 高阶(m)微分方程F(x,y,y,,y)=0, y=f(x,y,y,.v(D)
2. 微分方程的阶 一阶微分方程 F(x, y, y) = 0, y = f (x, y); 高阶(n)微分方程 ( , , , , ) 0, ( ) = n F x y y y ( , , , , ). ( ) ( −1) = n n y f x y y y 微分方程中出现的未知函数导数的最高阶数 称为微分方程的阶
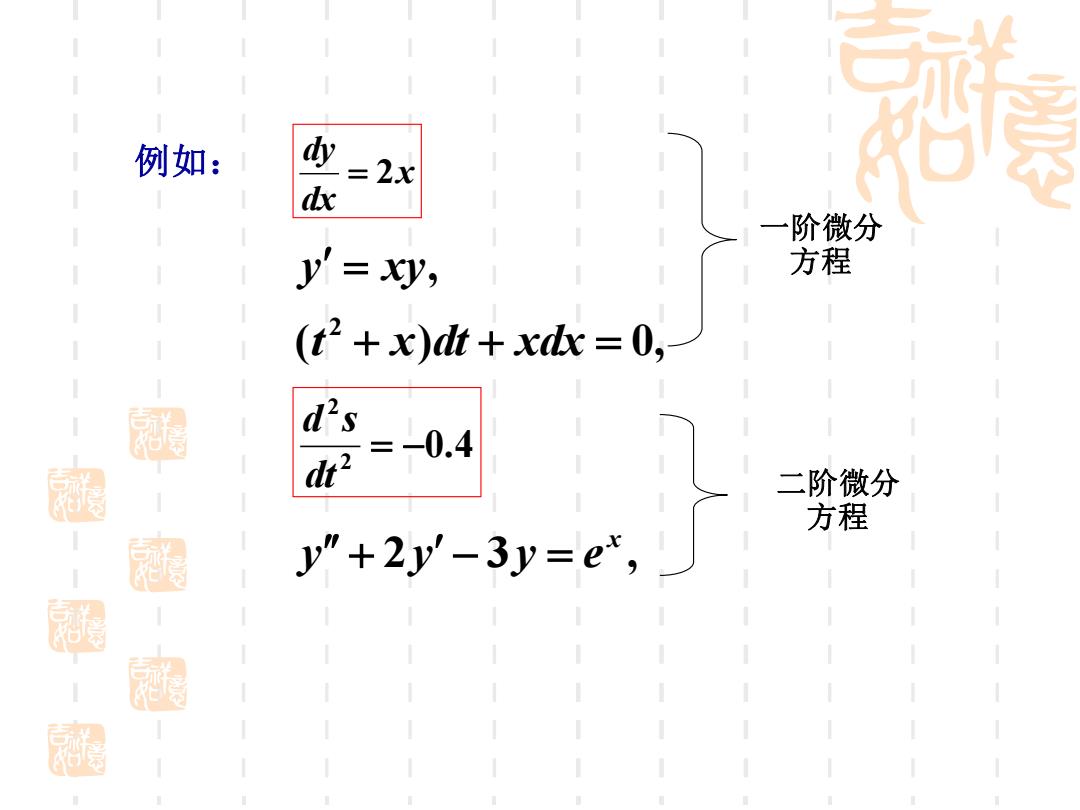
例如: y =2x d 一阶微分 y'=xy, 方程 (+x)dt+xdx= :0 ds -0.4 dr 二阶微分 y"+2y-3y=e, 方程
y = xy , ( ) 0, 2 t + x dt + xdx = 2 3 , x y + y − y = e 0.4 22 = − dt d s x dx dy = 2 一阶微分 方程 二阶微分 方程 例如:

3.线性微分方程 如果方程为y及y',…,ym 的一次有理整式 则称F(x,y,y',…y)=0为阶线性微分方程 例如: d2S =-0.4是二阶线性微分方程。 y'+P(x)y=Q(x),是一阶线性微分方程. x(y)2-2y'+x=0;不是线性微分方程. 般n阶线性微分方程具有形式 ym+a(x)y(++a(x)y'+a(x)y=f(x) 这里ac),,nc),fx)是x的已知函数. 不是线性方程的方程称为非线性方程
例如: 2 2 d 0.4 d S t = − 一般n阶线性微分方程具有形式 1 1 1 − − + + + + = ( ) ( ) ( ) ( ) ( ) ( ) n n n n y a x y a x y a x y f x ( ) , , n 如果方程为y及 y y 的一次有理整式, 是二阶线性微分方程. 这里a1 (x),…,an (x),f (x)是x的已知函数. 则称 0 为n阶线性微分方程. = ( ) , , , ) n F x y y y ( 不是线性方程的方程称为非线性方程. 2 x y yy x ( ) 2 0; − + = 3. 线性微分方程 不是线性微分方程. y + P(x) y = Q(x), 是一阶线性微分方程

4.微分方程的解 如果函数y=(x)代入微分方程,能 使微分方程变为恒等式,则称函数y=(x) 为方程的解 例如:函数S=-0.2t2+Ct+C,是方程 t"s =-0.4 dr 的解 涵 如果关系式D(x,y)=0决定的隐函数y=p(x) 是微分方程的解,则称(x,)=0为方程的 隐式解
为方程的解. 例如: 如果函数 y x = ( ) 代入微分方程,能 使微分方程变为恒等式,则称函数 y x = ( ) 如果关系式 ( , ) 0 x y = 决定的隐函数 y x = ( ) 隐式解. 是微分方程的解,则称 ( , ) 0 x y = 为方程的 函数 S t C t C = − + + 0.2 2 1 2 是方程 的解. 0.4 2 2 = − dt d s 4. 微分方程的解