
第二章 轨迹与方程 教学目的:理解曲线和曲面的解析表示和从点的轨迹思想导出解析方程的一般 方法:掌握母线平行于坐标轴的柱面方程的特点。 在平面上或空间取定了标架之后,平面上或空间的点就与有序实数组 (x,y)或(x,y,z)建立了一一对应的关系,在此基础上,我们将进一步建立 作为点的轨迹的曲线,曲面与其方程之间的联系,把研究曲线与曲面的几何 问题,归结为研究其方程的代数问题,从而为用代数的方法对一些曲线与曲 面进行研究创造了条件 §2.1平面曲线的方程 教学目的 1、理解平面曲线方程的定义。 2、掌握用向量法建立平面曲线的普通方程和参数方程的一般方法与 步骤。 3、理解几种重要的平面曲线的生成规律。 4、掌握一些平面曲线的普遍方程与参数方程的互化。 教学重点 用向量法建立平面曲线的普通方程和参数方程的一般方法与步骤。 教学难点 一些平面曲线的普遍方程与参数方程的互化。 教学内容 在这里,平面上的曲线(包括直线),都是看成具有某种特征性质的点的 集合,曲线上点的特征性质,包含着两方面的意思,就是:①曲线上的点都具 有这些性质:②具有这些性质的点都在曲线上.因此曲线上点的特征性质,也 可以说成是点在曲线上的充要条件, 曲线上点的特征性质,在建立了坐标系的平面上,它反映为曲线上点的 两个坐标x与y所应满足的相互制约条件,一般用方程F(x,y)=0或y=f(x) 来表达

定义2.1.1 当平面上取定了标架之后,如果一个方程与一条曲线有着 关系:①满足方程的(x,y)必是曲线上某一点的坐标:②曲线上任何一点的坐 标(x,y)满足这个方程,那么这个方程就叫做这条曲线的方程,而这条曲线叫 做这个方程的图形 为了方便起见,"点的坐标满足方程”这句话常说成”点满足方程”, 根据曲线方程的定义,曲线上的点与其方程的解之间有着一一对应关 系.这样,研究曲线的几何问题,就可以转化为研究其方程的代数问题了. 对于一条给定的曲线,要求出它的方程,实际上就是在给定的坐标系下, 将这条曲线上的点的特征性质,用关于曲线上的点的两个坐标x,y的方程来 表达,现举例说明于下: 例1求圆心在原点,半径为R的圆的方程, 解根据圆的定义,圆上任意点M(x,y)的特征性质,即M(x,y)在圆上 的充要条件是M到圆O的距离等于半径R,即|OM|=R.应用两点距离公 式,得 Va2+b2=R, (1) 两边平方得x2+y2=R2 (2.1-1) 由于方程(2.1-1)与(1)同解,所以(2.1-1)即为所求圆的方程. 完全类似地,可以求得圆心在(a,b)半径为R的圆的方程是 (x-a)^2+(yb)^2=R^2. 求曲线的方程,有时在化简过程中,会增添不属于给定条件的内容.这时, 必须从方程开始检查一下,把方程中代表那些不符合给定条件的点限制掉, 例2己知两点A(-2,2)和B(2,2),求满足条件|MA|-MB=4的动点M 的轨迹方程. 解 动点M在轨迹上的充要条件是|MA|-MB=4, 用点M的坐标(x,y)来表达就是 V(x+2)2+(y+2)2-V(x-2)2+y-2 2=4, (2)

移项得 V0x+2+v+2y-vx-2+v-2)+4 两边平方整理得 V(x-2)2+0y-2)2 =x+y-2, (3) 再两边平方整理得 xy=2. (4) 因为方程(2)与(3)同解,而方程(4)与(3)却不同解,但当方程(4)附加了条件 x+y-2≥0即x+y≥2后,方程(4)与(3)同解,从而方程(4)与(2)同解,所以 方程 xy=2,(x+y≥2) 为所求动点M的轨迹方程. 这里在方程xy=2中附加了条件x+y之2,其意思就是在方程xy=2中除去 使x+y<2的解,因为这些是不符合给定条件的多余的部分.所求的轨迹是反 比函数y=2/x的图象-一一一双曲线的一支,即第一象限中的部分. 在解析几何中,曲线又常常表现为一个动点运动的轨迹,但是运动的规 律往往不是直接反映为动点的两个坐标x与y之间的关系,而是直接表现为 动点的位置随着时间t改变的规律,当动点按照某种规律运动时,与它对应 的向径也将随着时间t的不同而改变(模与方向的改变),这样的向径我们称 它为变矢,记做r(t).如果变数t(a≤t≤b)的每一个值对应于变矢r的一个 完全确定的值(模与方向)r(t),那么我们就说r是变数t的矢性函数,并 把它记做r=r(t),a≤t≤b (2.1-3) 显然当t变化时,向量r的模与方向一般也都随着改变, 设平面上取定的标架为{0,el,e2},向量就可用它的分量来表达,这样矢 性函数(2.1-3)就可以写为r(t)=x(t)e1+y(t)e2,(a≤t≤b)(2.1-4)其 中x(t),y(t)是r(t)的分量,它们分别是变数t的函数

定义2.1.2若取t(a≤t≤b) 的一切可能取的值,由(2.1-4) 表示的向径r(t)的终点总在 P(x(t),y(t)) 一条曲线上:反过来,在这条 曲线上的任意点,总对应着以 r(a) 它为终点的向径,而这向径可 r(t) 由t的某一值t0(a≤t0≤b) r(b) 通过(2.1-4)完全决定,那么 X 就把表达式(2.1-4)叫做曲线 的向量式参数方程,其中的t为参数.换句话说,(2.1-4)叫做一条曲线的向 量式参数方程,如果当t在区间a≤t≤b内变动时,向径r(t)的终点 P(x(t),y(t))就描绘出这条曲线来 因为曲线上点的向径r(t)的分量为x(t),y(t),所以曲线的参数方程也 常写成下列形式 x=x(f) y=y(t) (a≤t≤b) (2.1-5) 我们把表达式(2.1-5)叫做曲线的饿坐标系参数方程 如果从(2.1-5)中消去参数t(如果可能的话),那么就能得出曲线的普通 方程 F(x,y)=0 与直线共线的非零向量V叫做直线的方向向量,显然,任何一个与直 线共线的非零向量,都可以作为直线的方向向量 「x=xo+X1 x-xo_y-Yo 由直线的参数方程y=+t消去参数1得X x-xo_y-Yo 方程XY 叫做直线的对称式方程或标准方程,它是一个二元 一次方程,可以把它写成Ax+By+C=0

这里A=y,B=-X,C=-(Y。-X). 反过来,任意一个二元一次方程Ax+By+C=0都表示直线,这是因为 x-Xo=y-Yo 它总能化成XY的形式。事实上,在方程Ar+By+C=0 中任取一组解心o,o,那么有Ax+By+C=0, x-xoy-yo 或 B -A」 方程Ax+By+C=0叫做直线的一般方程。从上面我们看到直线的一般 方程Ax+By+C=0中的系数A与B的几何意义是:向量4={B,-A 是直线Ax+By+C=0的一个方向向量,在直角坐标系下,显然有D= {A,B以垂直于向量9,从而p垂直于直线Ax+By+C=0,我们称 p={A,B}为Ax+By+C=0的法向量, 给定两直线 Ax+By+C=0 I2:A2x+B2y+C2=0 那么4与的方向向量分别为”={B,-A},”,={B,-A} 由两直线的方向向量读者容易知道两直线马与'2相交的充要条件为 A B 两直线【与'平行的充要条件为 A B2 C2 两直线马与'2重合的充要条件为

ABCL A,B2 C2 而在直角坐标系下,两直线与2的交角为 cos∠(4l2)=± 44,+BB 42+B24+B22 从而有 g<(44)=±4B-A,B AA,+BB, 例4一个圆在一直线上无滑动地滚动,求圆周上的一点的轨迹 图2-4 解 取直角坐标系,设 半径为的圆在x轴上滚动, 开始时点P恰好在原点O(图2-4) 经过一段时间的滚动,圆与直线的切点移到A点, 圆心移动到C的位置, 这时有 r=OP=0A+AC+CP 设0=·(CP,CA),于是矢量CP对轴所成的有向角为 ▣(,。-(+a)

则 Cp_ios+jawin0) 2 =(-asine)i+(-acos0)j. 又 :0A- =a0 .OA=a0i,AC=aj, 所以r=a(8-sin0)i+a(I-cos0)j是P点的轨迹的向量式参数方程,其 中B(-0<0<+0)为参数.设P点的坐标为(化,y),那么由 r=a(0-sinO)i+a(1-cos0)j容易得P点的坐标式参数方程为 (x=a(0-sin9(-n<0<+o) y=a(1-c0s0), 取0≤B≤π时,消去参数0,便得到P点的轨迹在0≤8≤π时的普通方程 x=aarccos- -y-V2a心y-y. x=a(e-sin), -0<0<+0) 这个方程要比参数方程y=a(1-cos), 复杂得多, 当这个圆在直线上每转动一周时,点P在圆周前后的运动情况总是相同 的,因此曲线是由一系列完全相同的拱形曲线组成(图2-5),这种曲线叫做 旋轮线或称为摆线, 图2-5

例5(内旋轮线)已知大圆半径为a,小圆半径为6,设大圆不动,而小 圆在大圆内无滑动的滚动,求动圆周上某一定点P的轨迹。此时动点的轨迹 叫做内旋轮线(或称内摆线)· 解:设运动开始时,动点P与两圆切点A重合,取大圆心0为原点,OA 为X轴建立坐标系(图26), 图26 经过某一个过程后,两圆切于B点,动圆心到C点,则C在OB上。 7=OP=0元+C2设8=L6,0C 则OC=a-bcos+im8D又设p=∠CP,C8,因为弧AB=孤BP a8=bp→p=2日 ∠d,=-(p-)=日-p= b-a日 所以 而 b p=bcosa-色i-bsma-bj 故 5 b i=a-bcos8+bcos8-产明+a-)smg-bsm- (-0<8<+0o) x=acos3g 特殊地,a=4时,曲线方程为y=a如39四尖点星形式(图27)
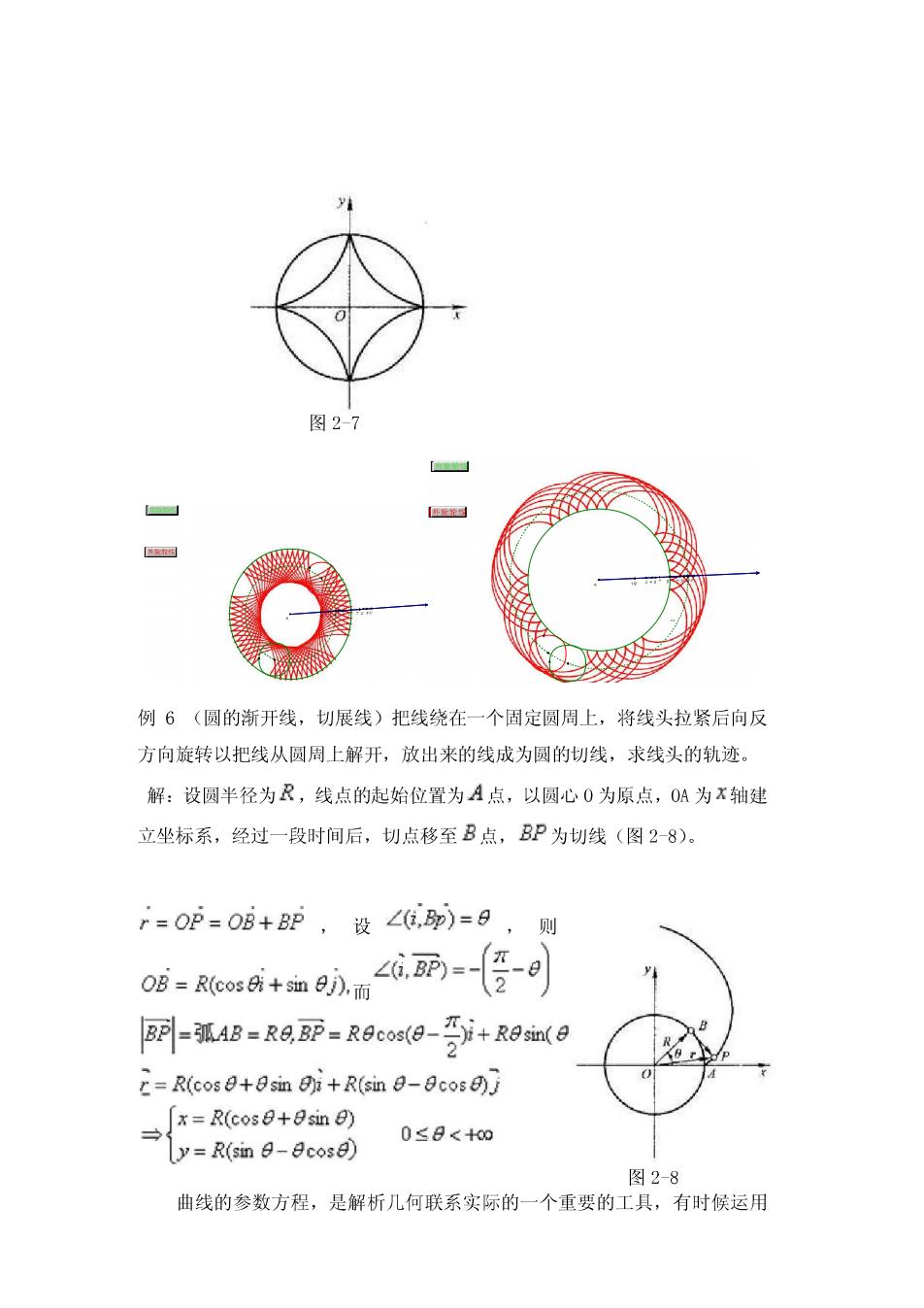
图2-7 卧旋养图 例6(圆的渐开线,切展线)把线绕在一个固定圆周上,将线头拉紧后向反 方向旋转以把线从圆周上解开,放出来的线成为圆的切线,求线头的轨迹。 解:设圆半径为R,线点的起始位置为A点,以圆心0为原点,OA为x轴建 立坐标系,经过一段时间后,切点移至B点,BP为切线(图28)。 r=0P=0B+BP,设∠,)=日, 则 OB=Rcos乐+sim9),而 丽={任- BPAB=R0.BP-ROcos(0-T)i+Rosin(0 =R(cos0+0sin 0)i+R(sin 0-0cos x=R(cos日+日sinθ) 0≤8<+o0 y=R(simn日-9cos8) 图2-8 曲线的参数方程,是解析几何联系实际的一个重要的工具,有时候运用

参数方程来表达曲线,要比普通方程简单得多,甚 至于有的曲线只能用参数方程来表示,而不能用普通方程表示,即不能 用七,y的初等函数来表示,例如参数方程 x=e'+t+lgt2, y =t+sint+arcsint, 便是这样的例子 消去曲线参数方程中的参数就得曲线的普通方程,反过来,我们也可以把 曲线的普通方程改写为参数方程的形式,一般地适当选取参数t,找出变数x 与参数1的关系式x=x(),然后代入原方程求出y=(),那么 x=x(),y=()就是曲线的参数方程.在这里当然也可先找出 屿的关系式y=y),然后代入原方程求出x=x(),从而得曲线的参数方程 x2,y2 例7把椭圆的饿普通方程a2+6 =1 改写为参数方程 解 设x=acos0,代入原方程得y=±bsin8,如果取y=-bsin日,令 0=-t,那么 x=acos0.v=-bsine 可以变形为 x=acost,y=-bsint 所以取日为参数,且-π≤日<π,那么椭圆的参数方程为 x=acos0 ly=bsin0 (-π≤8<π). 在化曲线的普通方程为参数方程时,由于选取的参数不是唯一的,所以关系 式x=x(t)可以有不同的形式,从而同一条曲线的参数方程也可以有多种表达 形式,例如在例7中,如果设 y=tx+b, x2.(x+b)2 =1. 代入原方程得 62 2a'bt x=0,x= 由此解得 b2+a2t2