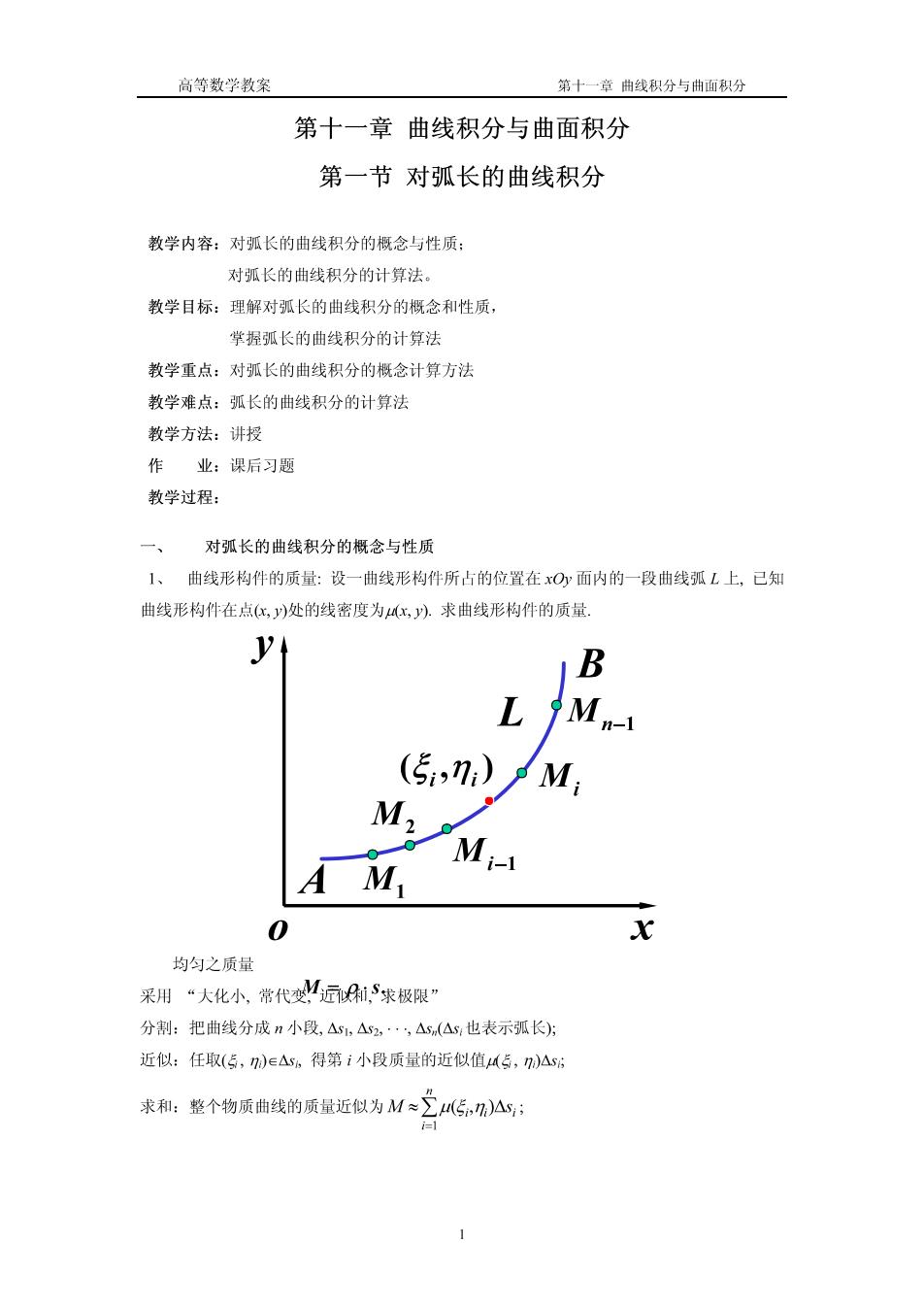
高等数学教案 第十一章曲线积分与曲面积分 第十一章曲线积分与曲面积分 第一节对弧长的曲线积分 教学内容:对弧长的曲线积分的概念与性质: 对弧长的曲线积分的计算法。 教学目标:理解对弧长的曲线积分的概念和性质, 掌握弧长的曲线积分的计算法 教学重点:对弧长的曲线积分的概念计算方法 教学难点:弧长的曲线积分的计算法 教学方法:讲授 作业:课后习题 教学过程: 一、 对弧长的曲线积分的概念与性质 1、曲线形构件的质量:设一曲线形构件所占的位置在xOy面内的一段曲线弧L上,已知 曲线形构件在点:,y)处的线密度为(x,y).求曲线形构件的质量. B Mn-1 (5,1) M M A M, 0 北 均匀之质量 采用“大化小常代变M远和,S求极限” 分割:把曲线分成n小段,△s,△s2,·△sn(△s也表示弧长)方 近似:任取(5,)E△s,得第i小段质量的近似值45,)△s 求和:整个物质曲线的质量近似为M≈2⑤,)△; i=1

高等数学教案 第十一章曲线积分与曲面积分 取极限:令m,-0,则整个物质前线的质量为M=m2以GA 1→01 这种和的极限在研究其它问题时也会遇到, 定义设L为xOy面内的一条光滑曲线弧,函数x,y)在L上有界.在L上任意插入一 点列M,M,·,Mn-1把L分在n个小段.设第i个小段的长度为△s,又(气,励为第i个小段 上任意取定的一点,作乘积点,As,(=l,2,·,n,并作和f传)△s,如果当各小弧 段的长度的最大值1→0,这和的极限总存在,则称此极限为函数x,y)在曲线弧L上对弧长 的曲线积分或第一类曲线积分,记作/c,达,即/,=im2f传,△s.其 中x,y)叫做被积函数,L叫做积分弧段. 曲线形构件的质量M=p(x,y,z的 2、曲线积分的存在性:当x,y)在光滑曲线弧L上连续时,对弧长的曲线积分 [f(x,)dk是 存在的.以后我们总假定x,)在L上是连续的 根据对弧长的曲线积分的定义,曲线形构件的质量就是曲线积分 (x,y)的值,其中 4(x,y)为线密度 对弧长的曲线积分的推广: Lfx.y.)ds-limm5)As, 20=1 根据对弧长的曲线积分的定义,如果曲线形构件L的线密度为x,y),则曲线形构件L 的质量为 [fx.yds 注意:(1)、如果L(或Γ)是分段光滑的,则规定函数在L(或Γ)上的曲线积分等于函数在 光滑的各段上的曲线积分的和.例如设L可分成两段光滑曲线弧L1及L2,则规定 Lds=fds+fyds (2)、闭曲线积分:如果L是闭曲线,那么函数x,y)在闭曲线L上对弧长的曲线积分 记作fx,还 (3)定积分是否可看作对弧长曲线积分的特例?发 否!!对弧长的曲线积分要求ds≥0但定积分中,dr可能为负。 对弧长的曲线积分的性质: [[cf(y)+czg(x,y)lds=c[f(x.y)ds+c2[g(x.y)ds; 性质2若积分弧段L可分成两段光滑曲线弧L1和L2,则

高等数学教案 第十一章曲线积分与曲面积分 dsds+ds; 性质3设在L上,g,以则∫fc,≤gx,还 特别地,有 fc,还华f,d 二、对弧长的曲线积分的计算法 基本思路:求曲线积分转化为计算定积分 另一方面,若曲线L的参数方程为x=),y=w()(≤, 则质量元素为 f(.y)ds=no(),v(ho()+v"()di, 曲线的质量为 f几o0,yto20+w2Gdh. 即 [f.yds-).vHo+di 定理设x,y)在曲线弧L上有定义且连续,L的参数方程为 x=0,=()(≤),其中0)、)在[a,月上具有一阶连续导数,且()+w()≠0,则 曲线积分∫fc,)还存在,且 [Sx.yds-A.vHo20+vd(p. 证明(略) 说明:(I):△S>0,.△1>0,因此积分限必须满足≤β 注意到ds=V(dx)2+(dy)2=√p2(t)+P(t)d1因此上述计算公式相当于“换元 法”。 应注意的问题:定积分的下限α一定要小于上限B. 讨论:()若曲线L的方程为=((a≤≤b),则f(x,)d=? 提示:L的参数方程为x=x,y=(x)(a≤≤b), [fx达=fxwW+w2(dk (2)若曲线L的方程为x=0c≤≤,则∫fx,)还=? 提示:L的参数方程为x=),yy(c≤d, f,s=f0),以p20W+1d. (3)若曲「的方程为x=40,=0,2=a0(a心,则f(化,y,2)d=?

高等数学教案 第十一章曲线积分与曲面积分 提示:「fx,yzd达=fIa0).y0,o0以o20)+w20)+aP0dt 例1计算∫VPd,其中L是抛物线=2上点00,0)与点B1,)之间的一段弧。 解曲线的方程为y=x2(0≤≤1),因此 =-Fi+-i4r65-0. 例2计算半径为R、中心角为2α的圆弧L对于它的对称轴的转动惯量1(设线密度为 e1). 解取坐标系如图所示,则I=[y2dk 曲线L的参数方程为x=Rcos0,)y=Rsin0(-a心), 于是I=Ly2b=.R2sin26V-Rsin02+(Rcos0d0 -R[sin2l0-R'(@-sinacos@). 例3计算曲线积分∫(r2+y2+z2)d还,其中T为螺旋线x=-acost、=-asint、2-k:上相应 于t从0到达2的一段弧。 解在曲线T上有x2+y2+z2=(acos)2+(asin)2+(k)2=a2+k2t2,并且 ds=(-asint)2+(acost)2+k2dt=a2+k2dt, 于是 [(2+y2+2ds =f"(a+k2P)l@+kd -号F+(62+4r2k. 例4计算x2ds,其中「为球面x2+y2+z2=a2被平面x+y+z=0所截的圆周。 解:由对称性可知 x'ds =fy'ds=f2ds fds-i+yds -ifods-ja'2xa 3a3。 小结:用曲线积分解决问题的步骤: (1)建立曲线积分; (2)写出曲线的参数方程(或直角坐标方程),确定参数的变化范围; (3)将曲线积分化为定积分; (4)计算定积分. 4