
第四章柱面、锥面、旋转曲面与二次曲面 本章介绍柱面、锥面、旋转曲面与二次曲面,其中柱面、锥面、旋转曲面具 有较为突出的几何特征,我们要从图形出发,讨论曲面的方程:二次曲面在方程 上表现出特殊的简单形式,我们将从它的方程出发,研究它的图形. 本章的知识结构为: 用形→方程; 方程 图形→曲面直纹性 柱面 椭球血 锥面 双曲面 旋转曲面 抛物血 4.1柱面 目的:通过本节的学习,使掌握两类平面束的概念及方程,能用平面束的性 质解决有关的问题. 重点:平面束的概念及方程 难点:有关定理的证明, 内容: 定义4.1.1在空间,一条以定方向为方向的直线沿着一条空间曲线C平行 移动时所形成的曲面称为柱面,其中1称为母线(母线不唯一),C称为准线(准 线也不唯一). 设柱面的准线C的方程为 F(x,y,z)=0, F(x,y,z)=0, (1) 母线方向为v={X,Y,Z 在柱面上任取一点M(x,八,2),那么M必在某一条母线L上,设L与准线C 的交点为M(:,),则L的方程为 x-x-y-上-2- Z, (2) 且有 F(x,y,z)=0 F(x,,z)=0 (3) (2)与(3)消去参数x1,y1,21,可得 F(x,y,z)=0 即为所求的柱面方程

特殊情沉,以1为对称轴的圆柱面,因为圆柱面上每一点到轴的距离都相 等(称为圆柱血的半径),所以它的准线可取成一个圆,母线方向与准线圆垂直. 例1柱面的准线为 x2+y2+z2=1 2x2+2y2+z2=2 而母线的方向为扩=《仁1,0,1,求这柱面方程 解设点M(x,八,2)是柱面上任意一点,则M必在某一条母线上,即存在 M,(化,,)为准线上一点,使得M,M∥v,即 x-=y-y=-五=1 …(1) -1 0 1 x1+y1+21=1 …(2) 2x12+2y2+z2=2 …(3) x1=x+1 少=y 则 21=z-1 代入(2),(3),即得t=z,代入(2)或(3), 得 (x+z)2+y2+(z-1)2=1 就是所求柱面的方程。 x=y-1=z+1 例2已知圆柱面的轴为1-2-2,点M,(1,-2,1)在此圆柱面上, 求这个圆柱面的方程。 解设点M(x,八,2)是柱面上任意一点,轴上点M(0,1,-) 半径r即M到轴的距离, ..r= 1MM×v_17 v 3 又因为M(x,y,)是柱面上任意一点, 则M到轴的距离也是半径r,即 x v-1 z+1 .r=MoMxv -2 -2 V(2x-2y+4)2+(2x+z+1)2+(2x+y-1)2V117 v 3 3 3 ∴.(2x-2y+4)2+(2x+z+1)2+(2x+y-1)2=117 就是所求圆柱面的方程

4.2锥面 目标:通过本节的学习,使了解锥面的有关概念,掌握锥血方程的求法, 重点:锥面方程的求法, 难点:锥面方程的求法, 内容: 定义42.1在空间中,由曲线C上的点与不在C上的一个定点Mo的连线组 成的曲面称为锥面(图4-1),称C为准线,称Mo为顶点,C上的点Mo与的连 线称为母线(母线不唯一)· 图4-1 已知锥面的准线C的方程为 F(x,,z)=0 F(x,y,z)=0 (1) 顶点M(y,2o),如果M,(,,)为准线上一点,那么过M的母线为: x-。=y-=2-0 x1-x0y-y0Z1-20, (2) 且 F(x,y1,3)=0.F(x,1,2)=0 (3) 从(2)与(3)中消去参数,最后可得一方程 F(x,y,z)=0 这就是所求的锥面的方程。 特别地,以I为对称轴的圆锥面,因为圆锥面上每一条母线与轴I的夹角都 相等(称为圆锥面的半顶角),它的准线可取成一个与轴垂直的圆(称为准线圆). 已知圆锥面的顶点、对称轴和半顶角,可简单地求锥血方程. 定理41.1一个关于x,y,2的齐次方程表示的曲面(添加原点)一定是以原点 为顶点的锥面, 推论一个关于x-xoy-%2-20的齐次方程表示顶点在(化yo20)的锥面. 例1锥面的顶点在原点,且准线为

0 Z=C 求这锥面方程, 解设点M(x,八,2)是锥面上任意一点,则M必在某一条母线上,即存在 M(x,,2)为准线上一点,使得M、M、原点在一直线上,即 x-0=y-0=2-0 =1 x1-0y1-0z1-0 2 且( 21=C 2=c1→1=2 =c ,h-c' 因此,所求锥面的方程为 x2 y2 22 a+6。=0 例2求以三根坐标轴为母线的圆锥面的方程 解显然,圆锥面的顶点为O(0,0),设轴的方向为'=(亿,m,) 因为三根坐标轴为母线,所以它们与轴的夹角相等,即 ICos∠(i,)HCos∠(,)HCos∠(k,) livljvkv vvv 即 171=1ml=Inl, 所以取 v=1,1,1)(或1,1,-1),(1,-1,10,1,-1,-1)可类似讨论) 设点M(x,y,z)是锥面上任意一点,所以 1C0s∠(i,)HCos∠(oM,1li-_1oMi.L 1 x+y+Z vOM 55x2+y2+z 因此,所求锥面方程为 (x+y+z)2=x2+y2+z2 4.3旋转曲面 目标:通过本节的学习,使掌握旋转曲面的有关概念,熟练掌握旋转曲血方 程的求法,了解几个常见的旋转曲面. 重点:旋转曲血方程的求法 难点:旋转曲血方程的求法 内容: 定义4.3.1在空间,一条曲线C绕着定直线1旋转一周所产生的曲面叫旋转 曲面其中1称为旋转轴,C称为母线 显然,母线上任意一点在旋转时形成一个圆,该圆与轴垂直,称为纬圆过 轴的半平面与旋转曲面的交线成为经线.每一条经线均可作为母线

下面,已知母线C的方程为 F(x,y,z)=0 F2(x,y,z)=0 (1) 旋转轴1为 X-x0=y-y0=2-20 X Y Z, (2) 求旋转曲面的方程. 分析:设点M(x,,)是旋转曲面上任意一点,则存在M(x1,y,21)为母线上 一点,使得M是由M1旋转而来,满足M,M到轴的距离相等(或到轴上任意一 点的距离相等),且MM1⊥1, F(x,y,z)=0 F(x,y,z)=0 Vx1-x)2+(y,-y)2+(31-z)2=V(x-x)2+(y-y)2+(z-z0)月 则 X(x-x)+Y(y-y1)+Z(z-z)=0 消去参数,,21,最后得 F(x,y,z)=0 即为所求的旋转曲面方程. xy z-I 例1求直线210绕直线1:x=y=z旋转一周所得的旋转曲面的方程. 解设点M(x,八,2)是旋转曲面上任意一点,则有在M1(化1,1,)为母线上一 点,使得M是由M1旋转而来,满足M,M1到轴的距离相等(或到轴上任意一点 的距离相等),且MM1⊥I,所以可得: 龙=出=-1 21 0 x2+y2+z2=x2+y2+z2 1(x-x)+1y-)+1(z-z)=0 消去参数x1,,2得所求旋转面为 x2+y2+z2-1=2(x+y+z-1)2 9 我们讨论在同一坐标面上的曲线绕其坐标轴旋转一周所成的旋转曲面的方 程 设母线C的方程为 F(y,z)=0 x=0 旋转轴1为z轴,求旋转曲面的方程. 分析:设点M(x,八,2)是旋转曲面上任意一点,则存在M(0,y,乙)为母线 上一点,使得M是由M1旋转而来,满足M,M1到轴的距离相等(或到轴上任意
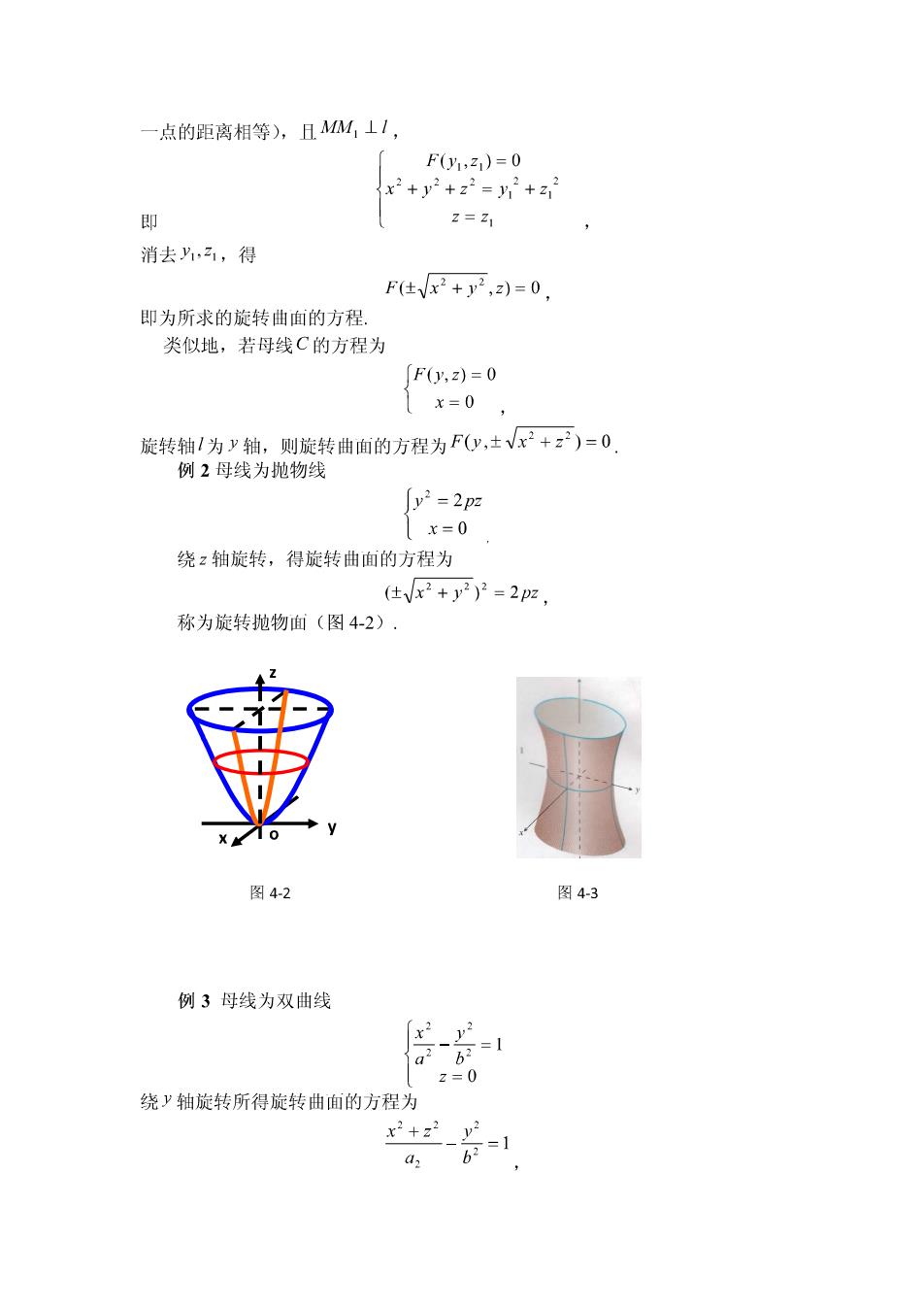
一点的距离相等),且MM,⊥1, F(y1,z1)=0 t +y2+z2=2+z2 即 z=21 消去y,1,得 F(仕Vx2+y2,z)=0. 即为所求的旋转曲面的方程。 类似地,若母线C的方程为 F(y,z)=0 x=0 旋转轴I为y轴,则旋转曲面的方程为Fy,±Vx2+z2)=0 例2母线为抛物线 y2=2pz x=0 绕z轴旋转,得旋转曲面的方程为 (仕Vx2+y2)2=2pz, 称为旋转抛物面(图4-2). 图4-2 图4-3 例3母线为双曲线 x2 y2 a2621 2=0 绕y轴旋转所得旋转曲面的方程为 x2+22 y2 42 62≈1

称为旋转单叶双曲面(图4-3):绕x轴旋转,得旋转曲面的方程为 xi+z 42b2 -=1 称为旋转双叶双曲面(图4-4). 图4-4 例4母线 (x-0)2+z2=r2 y=0 (0<r<a) 绕z轴旋转,得旋转曲面的方程为 (tVx2+y2-a)2+z2=r2 这样的曲面叫环面. 4.4椭球面 目标:通过本节的学习,使了解椭球面的概念及方程,熟练掌握椭球面的性 质和截线的形状及方程. 重点:椭球面的性质和截线的形状及方程, 难点:截线的形状及方程, 内容: 定义4.4.1在空间直角坐标系下,由方程的方程 x2y2z2 。+6+。= (4.4-1) 所表示的曲面叫椭球面,方程(4.4-1)叫椭球面的标准方程,其中a,b,c均为任 意的正常数, 椭球面有以下主要性质: 1°关于坐标原点、坐标轴、坐标面都对称. 2°|xKa,|yb,zc,并有六个顶点(±a,0,0),(0,±b,0),(0,0,+c). 3°三个主截线都是椭圆(图4-5),方程分别如下: 与xOy的交线

t a2 s1 z=0 (1) 与xOz的交线 y=0 (2) 与yOz的交线 x=0 (3) 4°与平行于xOy的平面z=h的交线 621、2 z=h (4) 图4-5 容易知道(4)图形的两轴的端点分别在椭圆(2)与(3)上。因此,椭球 面可以看成是由一个椭圆的变动(大小位置都改变)而产生的,这个椭圆在变动 中保持所在平面与xO少面平行,且两轴的端点分别在另外两个定椭圆(2)与(3) 上滑动: 特别的,在方程(4.4-1)中,若a=b时,椭球面的方程为 x2,y2,z2 a+a+-1(ac>0) 这是一个旋转椭球面。 4.5双曲面 目标:通过本节的学习,使了解双曲面的概念及方程,熟练掌握双曲面的性 质和截线的形状及方程. 重点:双曲面的性质和截线的形状及方程

难点:截线的形状及方程 内容: 1.单叶双曲面 定义4.5.1在空间直角坐标系下,由方程 x2,y2 (4.5-1) 所表示的曲血叫单叶双曲面(图4-6),方程(4.5-1)叫单叶双曲面的标准方程, 其中a,b,c均为正数. 图46 图4-7 对于单叶双曲面有下列性质: 1°关于坐标原点、坐标轴、坐标面都对称。 2°有四个顶点(±a,0,0),(0,±b,0) 3°与三坐标面的交线的形状(图4-7): x2y2 与xOy的交线 z=0 (1)是一个椭圆: x222 a-c=1 与xOz的交线 0y=0 (2)是双曲线: y2 22 与Oz的交线 x=0 (3)是双曲线. 4°与平行于xOy的平面z=h的交线 x2 631、 z=h (4)是一个椭圆. 50与平行于xOz的平面y=h的交线

c21、h 22 y=h (5)是双曲线 容易知道图形(4)的两对顶点分别在双曲线(2)与(3)上。因此,单叶 双曲面可以看成是由一个椭圆的变动(大小位置都改变)而产生的,这个椭圆在 变动中保持所在平面与0少面平行,且两对顶点分别沿着两个定双曲线(2)与 (3)上滑动 x2y2 特别地,若a=b,a a2-c2=1(a,c>0) 是一个单叶旋转双曲面, 2.双叶双曲面 定义4.5.2在空间直角坐标系下,由方程 x2 y2 22 +6。 (4.5-2) 所表示的曲血叫双叶双曲面(图4-8),方程(4.5-2)叫双叶双曲面的标准方程, 其中a,b,c均为正数. 图4-8 图49 双叶双曲面有以下主要性质: (1)关于坐标原点、坐标轴、坐标面都对称. (2)只与z轴相交,有两个顶点(0,0,±c). (3)形状: a- c?=-1 与xOz的交线 (y=0 (6)是双曲线, y222 与yOz的交线 x=0 (7)是双曲线. 与平行于O少的平面z=h的交线