
第3章平面与空间直线 §3.1平面的方程 1.求下列各平面的坐标式参数方程和一般方程: (1)通过点M1(3,1,-1)和点M,(1,-1,0)且¥行于矢量{-1,0,2}的平面(2)通过点 M,1,-5,)和M,(3,2,-2)月垂直于xoy坐标面的Ψ面: (3)已知四点A(5,1,3),B1,6,2),C(5,0,4)D(4,0,6)。求通过直线AB且¥行于直线 CD的平面,并求通过直线AB月与△ABC平面垂直的平面 解:(1)MM2={-2,-2,1},又矢量{-1,0,2}平行于所求平面, 故所求的半面方程为: x=3-2u-y y=1-2u z=-1+M+2y 一般方程为:4x-3y+2z-7=0 (2)山于半面垂直于xoy面,所以它平行于z轴,即{0,0,1}与所求的半面平行,又 MM,={2,7,-3},平行于所求的平面,所以要求的半面的参数方程为: x=1+2u y=-5+7u z=1-3+v 一般方程为:7(x-1)-2(y+5)=0,即7x-2y-17=0。 (3)(i)设Y面π通过直线AB,月平行于直线CD: AB={-4,5,-1},CD={-1,0,2} 从而π的参数方程为: x=5-4u-v y=1+5w z=3-M+2y 一般方程为:10x+9y+5z-74=0。 (iⅱ)设平面π'通过直线AB,月垂直于△ABC所在的平面 .AB={-4,5,-1},AB×AC={-4,5,-1}×{0,-1,1={4,4,4}=4{1,1,1}

均与π'平行,所以π'的参数式方程为: x=5-4l+v y=1+5u+v z=3-u+v 一般方程为:2x+y-3z-2=0. 2化一般方程为截距式与参数式: π:x+2y-z+4=0. 解:π与三个坐标轴的交点为:(-4,0,0),(0-2,0),(0,0,4), 所以,它的截距式方程为:文+ y+2=1. 一十 -4-24 又与所给平面方程平行的矢量为:{4,-2,0},{4,0,4}, .所求平面的参数式方程为: x=-4+2w+y y=-4 Z=v 3.证明矢量v={X,Y,Z}半行与平面Ax+By+Cz+D=0的充要条件为: AX+BY+CZ=0. 证明:不妨设A≠0, 则平面Ax+By+Cz+D=0的参数式方程为: x=-D-Bu-Cv -W- AA”A y=u Z=V B C 故其方位矢量为:人1,0,0,, A 从而v平行于平面Ax+By+Cz+D=0的充要条件为: X Y Z (月10,-0y共面台 C B 10=0 C 01 台AX+BY+CZ=0

4.已知:连接两点A(3,10,-5),B(0,12,z)的线段平行于Ψ面7x+4y-z-1=0,求B甲的 坐标z. 解: AB={-3,2,5+z} 而AB平行于7x+4y-z-1=0 h题3知:(-3)×7+2×4-(z+5)=0 从而z=18. §3,2平面与点的相关位置 1.计算下列点和平面间的离差和距离: (1)M(-2,4,3),π:2x-y+2z+3=0: (2)M1,2,-3),π:5x-3y+z+4=0. 解:将π的方程法式化,得: 2.12 x+3 z-1=0, 3 放离差为:òM0=有×-2)+×4-2x3-1 2 1 3 3 3 M到π的距离d=5(M=3 (2)类似(1),可求得 dM)=- 5 6 34 3sV353555=0, M到π的距离d=6(M)=0. 2.求下列各点的坐标: (1)在y轴上且到平面2+2y-2z-2=0的距离等于4个单位的点: (2)在z轴上月到点M(1,-2,0)与到Ψ面3x-2y+6z-9=0距离相等的点: (3)在x轴上月到Ψ面12x-16y+15z+1=0和2x+2y-z-1=0距离相等的点。 解:(1)设要求的点为M(0,y。,0)则山题意

2y-2-4 √9 .y。-1=6→yo=-5或7. 即所求的点为(0,-5,0)及(0,7,0)。 (2)设所求的点为(0,0,z。)则山题意知: +22+-6。-9 7 山此,z。=-2或-82/13。 故,要求的点为(0,0,-2)及0,0,-82 31 (3)设所求的点为(x。,0,0),山题意知: 12×0+1-2x。- 25 3 山此解得:x。=2或11/43。 所求点即(2,0,0)及(11/43,0,0)。 3.已知四面体的四个项点为S(0,6,4),A(3,5,3),B(-2,11,-5),C(1,-1,4),计算从顶点S向底 面ABC所引的高。 解:地面ABC的方程为: 2x-y-2z+5=0 所以,高h=上6-2×4+5-3. 3 4.求中心在C(3,-5,2)月与平面2x-y-3z+11=0相切的球面方程。 解:球面的半径为C到平面π:2x-y-3z+11=0的距离,它为: R-2×3+5+6+1l-28=24, V14 V14 所以,要求的球面的方程为: (x-3)2+y+5)2+(z+2)2=56. 即:x2+y2+z2-6x+10y+4z-18=0

3.3两平面的相关位置 1.判别下列各对直线的相关位置: (1Dx+2y-4z+1=0与+)-2-3=0: 42 (2)2x-y-2z-5=0与x+3y-z-1=0: 9 (3)6x+2y-4z-5=0与9x+3y-62-2=0: 11 解:(1)1:2:(-4)=二:三:(-1),∴.(1)中的两Ψ面Ψ行(不重合: 42 (2):2:(-1):(-2)≠1:3:(-1),(2)中两Ψ面相交: (3)6:2:(-4)=9:3:(-6),.(3)中两Ψ面平行(不重合)。 2.分别在下列条件下确定1,m,n的值: (1)使(1-3)x+(m+1)y+(n-3)z+8=0和(m+3)x+(n-9)y+(1-3)z-16=0表 示同一平面: (2)使2x+my+3z-5=0与lx-6y-6z+2=0表示二¥行平面: (3)使x+y-3z+1=0与7x+2y-z=0表示二互相垂直的平面。 解:(1)欲使所给的二方程表示同一平面,则: 1-3m+1n-38 m+3n-91-3-16 即: m+21-3=0 n+2m-7=0 1+2n-9=0 人之 13 37 从而: ,m= 9 9n= 9 (2)欲使所给的二方程表示二半行半面,则: 2=m=3 /-6-6 所以:1=4,m=3。 (3)欲使所给的二方程表示二垂直平面,则: 71-2+3=0 所以:1=一7

3.求下列两平行平面间的距离: (1)19x-4y+8z+21=0,19x-4y+8z+42=0: (2)3x+6y-2z-7=0,3x+6y-2z+14=0。 解:(1)将所给的方程化为: 194 x+ 8 -1=0 212121 1948 21x+27)-2 -x+ z-2=0 所以两平面间的距离为:2-1=1。 (2)同(1)可求得两平行平面间的距离为1+2=3。 4.求下列个组平面成的角: (1)x+y-11=0,3x+8=0: (2)2x-3y+6z-12=0,x+2y+2z-7=0。 解:(1)设π1:x+y-11=0,π2:3x+8=0 :c0sa,)3=t2 √2×32 ·π,)=或z 44 (2)设π1:2.x-3y+6z-12=0,π2:x+2y+2z-7=0 c0s(元,元,)=t2-6+12-+8 =土 7×321 ∠,,)=c0s8别或∠,,)=T-60s8到 21 21 §3.4空间直线的方程 1.求下列各直线的方程: (1)通过点A(-3,0,1)和点B(2,-5,1)的直线: (2)通过点M(xo,yo,2o)月平行于两相交平面π,: Ax+By+Cz+D=0 (i=1,2)的直线:

(3)通过点M1-5,3)月与x,八,z三轴分别成60°,45°,120°的直线: (4)通过点M0,0-2)月与两直线一l=上=2+和兰=y-1-+1垂直的直线: 1=1=-1和-10 (5)通过点M(2,-3,-5)月与平面6x-3y-5z+2=0垂直的直线。 解:(1)山本节(3.46)式,得所求的直线方程为: x+3=y=2-1 2+3-50 1-109 (2)欲求直线的方向矢量为: 海,8: 所以,直线方程为: X-Xo V-Yo B B> C, C,4. 4,B. (3)欲求的直线的方向矢量为: kas0cos45.}合是-}司 故直线方程为: x-1_y+5z-3 1√2-1 (4)欲求直线的方向矢量为:1,1,-1}×1,-1,0}={1,-1,-2}, 所以,直线方程为: x-1_y_z+2 11-2 (5)欲求的直线的方向矢量为:6,-3,-5}, 所以直线方程为: x-2=y-3-2+5 6-3 -59 2求以下各点的坐标: (1)在直线X一=y一8=一8上与原点相距25个单位的点: 213 (2)关于直线 x-y-4红+12=0与点P2,0-)对称的点- 2x+y-2z+3=0 解:(1)设所求的点为M(x,y,z),则:

x=1+21 y=8+1 z=8+31 又x2+y2+z2=252 即:(1+2)2+(8+t)2+(8+3)2=252, 解得:1=4或-62 所以要来的点的标为9120(-,号-19。 (2)已知直线的方向矢量为:1,-1,-4}×{2,1,-2}={6,-6,3},或为2,-2,1, .过P垂直与已知直线的半面为:2(x-2)-2y+(z+1)=0, 即2x-2y+z-3=0, 该平面与已知直线的交点为(I,1,3),所以若令P'(x,y,z)为P的对称点,则: 、12+x,1=2’22 2 2 x=0,y=2,z=7, 即P'(0,2,7)。 3.求下列各平面的方程: (1)通过点p(2,0.-),月又通过直线+1-二=2-2的¥面: 2-13 (2)通过直线x=2-y+3-+月与直线 1 -5 -1 2x-y-z-3=0 x+2y-z-5=0 平行的平面: (3)通过直线X二1=y+2=2二2月与半面3x+2y-2-5=0垂直的Y面: 2-32 5x+8y-3z+9=0 (4)通过直线 向三坐标面所引的三个射影半面。 2x-4y+z-1=0 解:(1)因为所求的平面过点p(2,0,-1)和p'(-1,0,2),月它半行于矢量{2,-1,3},所以要 求的平面方程为:

x-2 y z+ 2 0 即x+5y+z-1=0。 (2)已知直线的方向矢量为{2,-1,1}×1,2,-1}={-1,3,5}, ,半面方程为: x-2y+3z+1 -5 -1=0 3 5 即11x+2y+z-15=0 (3)要求平面的法矢量为2,-3,2}×3,2,-1}={-1,8,13}, ∴.半面的方程为:(x-1)-8(y+2)-13(z-2)=0, 即x-8y-13z+9=0。 5x+8y-3z+9=0 (4)山已知方程 2x-4y+z-1=0 分别消去x,y,z得到: 36y-11z+23=0,9x-z+7=0,11x-4y+6=0 此即为三个射影半面的方程。 4.化下列直线的一般方程为射影式方程与标准方程,并求出直线的方向余弦: 2x+y-z+1=0 x+z-6=0 (1) (2) 3x-y-2z-3=0 2x-4y-z+6=0 x+y-z=0 (3) x=2 解:(1)直线的方向数为: :非 -3 -2 X= 2+ ∴射影式方程为: 5 -5 19 5 -5
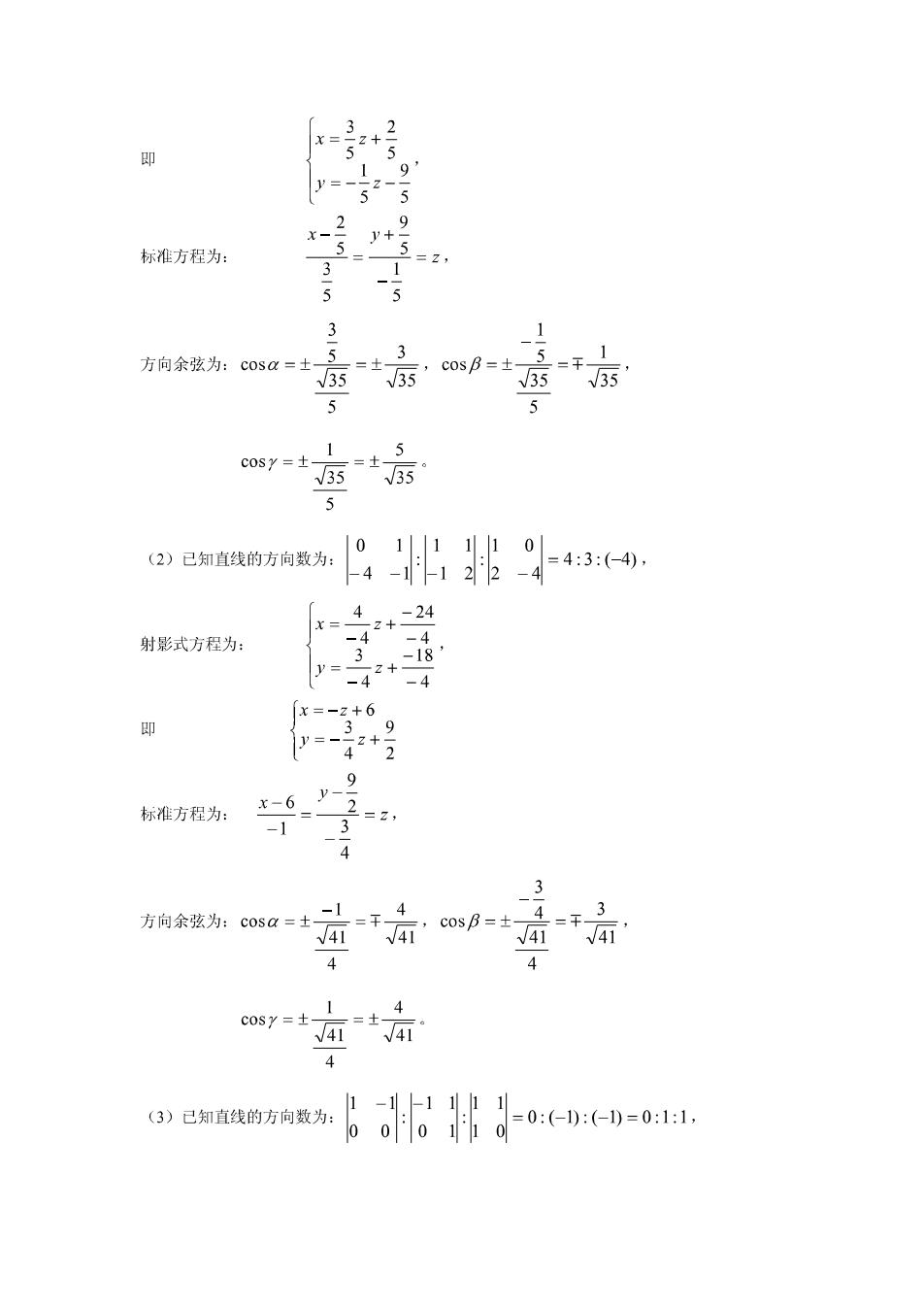
3 x= Z+ 2 即 5 1 9 1= 5 2 9 x- + 标准方程为: 5 3 =Z, 1 1 方向余弦为:cosa= 5 ¥、3 ,Cosf=± 5 1 V35 V35 V3 √35 J 5 1 5 c0sy=± =土 √35 V35 J (2)已知直线的方向数为 4 -24 X= z+ 射影式方程为: -4 4 3 -18 y= Z+ -4 -4 x=-z+6 即 3 9 -Z+ 4 标准方程为: x-6 y- 2 =Z, -1 3 4 3 方向余弦为:c0sa=t-1 、4 F,CosB=±4 3 √41V4 W41 V41 4 4 cosy=t 4 V41 V41 4 (3)已知直线的方向数为: 6.6o(0)-01