
高等数学教案第八章 空间解析几何与向量代数 第八章习题及实验课 例1已知三角形的顶点为A(1,2,3),B(7,10,3)和C(-1,3,1)。 试证明A角为钝角。 证4B=(7-1)2+(10-2)2+(3-3)2=100 AC=(-1-102+(3-2)2+(1-3)2=9 BC=(7-(-10)2+(10-3)2+(3-1)2=117 可见,|BC>AC+AB由余弦定理,就可知A角为钝角。 例2在z轴上,求与A(-4,1,7)和B(3,5,-2)两点等距离的点。 解设M为所求的点,因为M在z轴上,故可设M的坐标为:(0,0,z) 根据题意,及√(0-(-4)2+(0-1)2+(2-7)2=V(0-3)2+(0-5)2+(z-(-2) 去根号,整理得:z=14/9 ∴.M(0,0,14/9)。 例3试在xoy平面上求一点,使它到A(1,-1,5)、B(3,4,4)和C(4,6,1)各点的 距离相等。 解设M为所求。故依题意可设M的坐标为(x,y,0),又由题意知: MA=MB=MC,即: Vx-1)2+0y+1)2+(0-5)2=x-3)}2+0y-42+0-42=Vx-42+0y-62+0-10 化简可得 ∫4x+10y=14∫x=16 2x+4y=121y=-5

高等数学教案第八章 空间解析几何与向量代数 .所求的点为M(16,-5,0)。 例4已知平面上一点P1(a,0,0),P2(0,b,0),P3(0,0,c)。若:abc≠0, 求平面π的方程: 解PE={-a,b,0},PE={-a,0,c} 方利 则方=PE×PE -a b 0=bci+acj+abk -a 0 c 则:bc(x-a)+ac(y-0)+ab(z-0)=0 同除以abc则x+上+三=1 a b c 其中a,b,c称为平面π方程在x轴,y轴,z轴上的截距。 例5设平面π过原点以及点(6,-3,2),且与平面4x-y+2z=8垂直,求平面 π的方程。 解〖法一:由于平面π过原点,所以可设平面π的方程为:Ax+By+Cz=0。 则 61-3B+2C=0,上面两式相减得AB,C=-B,任取B-2,A=B=2, 4A-B+2C=0 2 C=-3 ∴.平面π的方程的为:2x+2y-3z=0 〖法二〗设平面π的法向量为方,而其余两平面的法向量依次记做:元,,,。 且n={6,-3,2},n2={4,-1,2} ∴.=元×元2=6-3 2 =-4i-4j+6k 4-12 2

高等数学教案第八章 空间解析几何与向量代数 ∴.平面π的方程的为2(x-0)+2(y-0)+3(z-0)=0. 例6设点P1(x1,y1,z)为平面π:Ax+By+Cz+D=0外的一点。求点P1到 平面π的距离d。 解设Po(xo,yo,Zo)为平面π上的任意一点。又设设平面π的法向量为元, 而直线PP的方向向量为ā: d=P.Rlcos(.)=PRl.)+BCY-)+C(=z) PoPV4+B+C 又,Axo+Byo+CZ0=-D :d++C2+D VA2+B2+C2 如:P1(1,1,2)到平面:3x-2y+z1=0的距离为d4 4 例7求过点P2,1,3)且与直线:-”7-,垂直相交的直线1的 352 方程。 解不妨设两直线交点为M(X0,y0,Z0), x0=3t 由于M在11上,故: y0=5t-7,其中t为参变量。 20=2t+2 由于直线l与直线:垂直: 其中直线】:的方向向量为三={3,5,2},而直线1的方向向量为: s={x。-2,yo+1,2。-3}={3-2,51-6,21-1} .5·=3(3t-2)+5·(5t-6)+2(2t-1)=0

高等数学教案第八章 空间解析几何与向量代数 .t=1 从而M点坐标为(3,-2,4),则={1,-1,1 则直线1的方程:x-2=y+1_2-3 1-11 例8设: ,》=0,求以T作为准线,母线平行于z轴的柱面方程。 z=0 解 在柱面上任意取一点M(xo,y0,Z0),则M必在某条母线上,它与「的交点 为M1(xo,,0)(如下图),从而有p(xo,yo)=0,故曲面上任一点都满足 M 图 p(x,y)=0: 另一方面:若M(xo,yo,zo)满足p(xo,yo)=0,则M必在经过 C(x0,y0,0)的母线上,且Z0. 故所求柱面方程为p(x,y)=0。 【注】此表达式中,缺z。 同理:以 (x,)=0,0,2)=0为准线,母线分别平行于y,z y=0 x=0 轴的柱面方程分别为(x,z)=0,py,z)=0。 其中,y2+z2=2代表母线平行于x轴的圆柱面: 4
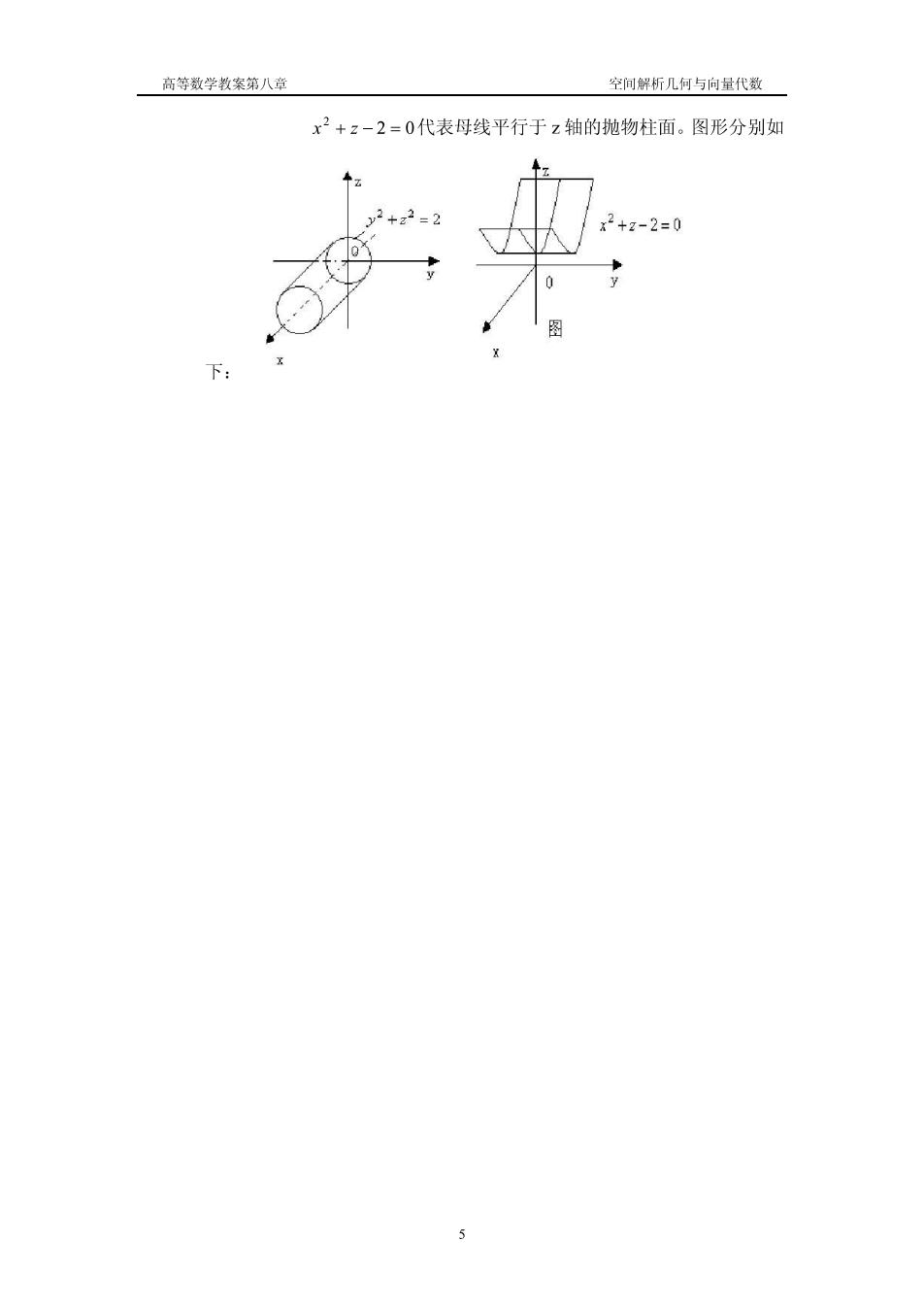
高等数学教案第八章 空间解析几何与向量代数 x2+z-2=0代表母线平行于z轴的抛物柱面。图形分别如 y2+22=2 +3-2=0 图 下: