
1.2极限 g1.2.1数列的极限 g1.2.2i 函数的极限 1.2.3无穷小与无穷大 1.2.4极限的运算法则 晟秘私 1.2.5两个重要极限
1.2 极 限 1.2.1 数列的极限 1.2.2 函数的极限 1.2.3 无穷小与无穷大 1.2.4 极限的运算法则 1.2.5 两个重要极限
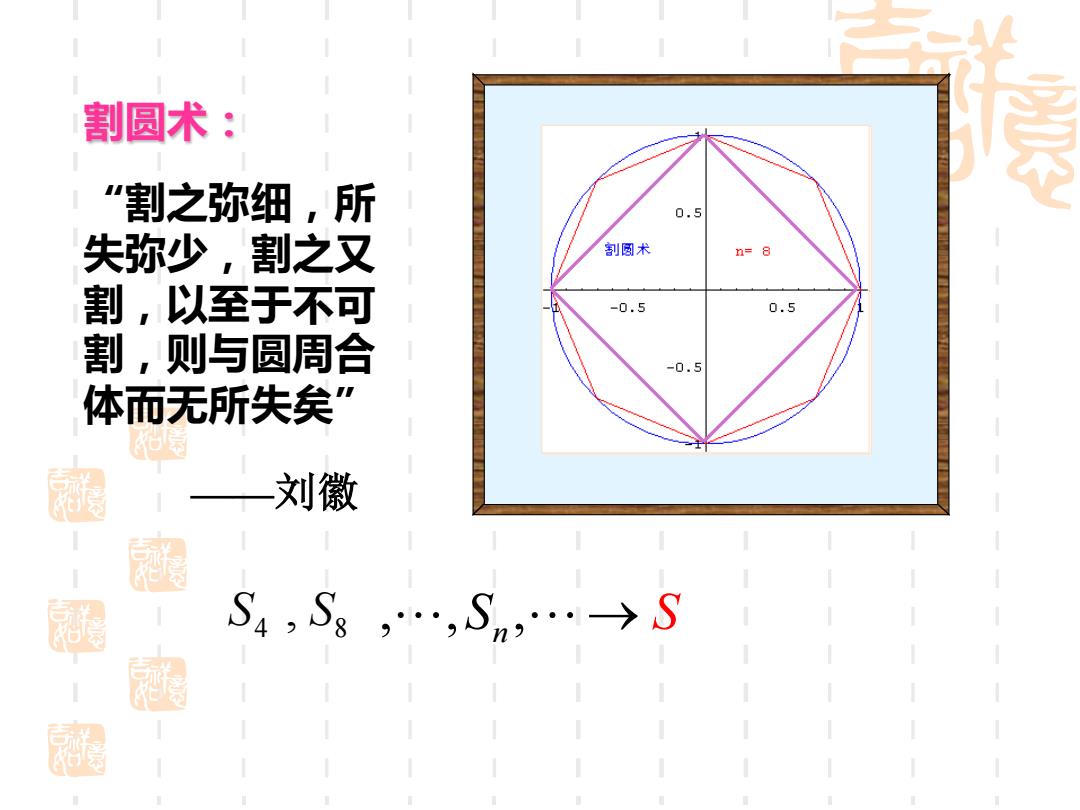
割圆术 割之弥细,所 0.5 失弥少,割之又 割圆术 n=8 割,以至于不可 -0.5 0.5 割,则与圆周合 -0.5 体而无所失矣” 湿 一刘徽 S4,Sg,…,Sn,…→S
割圆术: “割之弥细,所 失弥少,割之又 割,以至于不可 割,则与圆周合 体而无所失矣” ——刘徽 4 S , , , n , S8 S → S

1.2.1数列的极限 数列的概念:我们称按照一定法则排列的无穷 多个实数x1,x2,…,xm,…为数列。 或简记为{x,数列中的每一个数称为数列的 项,x称为数列的一般项或通项, 数列可以看作是以正整数集为定义域的一种特 殊的函数
1.2.1 数列的极限 或简记为{xn }, 数列中的每一个数称为数列的 项,xn称为数列的一般项或通项. 数列的概念:我们称按照一定法则排列的无穷 多个实数 x1 , x2 , , xn , 为数列。 数列可以看作是以正整数集为定义域的一种特 殊的函数

必例1 0份 →0 ah+旷}y →1 凝 (3){-1)}:1-1,1,(-, →? (4){2n}:2,4,6,…,2n,… >+00 程
例1 ( ) 1 1 1 1 1 : 1, , , , , n n 2 3 ( ) ( ) ( ) 1 1 5 7 1 2 1 1 : , , , ,1 1 , 2 2 4 8 2 n n n n + − + − → 0 →1 ( ) ( ) ( ) 1 1 3 1 : 1, 1,1, , 1 , n n − − − − − (4 2 : 2, 4,6, , 2 , ) n n → ? →+

1.2.1数列的极限 定义1-4 若数列x1,x2,x3,,xw.,当项数n无限增 大时,它的通项xm无限趋近于某一个常数a, 则称为数列{x的极限。记作 lim x n->oo 剂 或m→a(n→+o)。 具有极限的数列称为收敛数列,没有极限 的数列称为发散数列
1.2.1 数列的极限 若数列x1 , x2 , x3 , …, xn ,…,当项数n无限增 大时,它的通项xn无限趋近于某一个常数a, 则称a为数列{xn }的极限。记作 或 xn→a (n→+∞)。 具有极限的数列称为收敛数列,没有极限 的数列称为发散数列。 x a n n = → lim 定义1-4

1 lim=0 n→on limg"=0(lqo0 不存在
1 lim 0 n→ n = lim 0 1 . ( ) n n q q → = 1 lim 1 ( 1) 1 2 n n n→ + − = lim 2 n n → = + ( ) 1 lim 1 n n − → − 不存在

[几点说明] 1.数列的收敛与否与这个数列的增减性无关 常数列一定是收敛数列。limC=C n-→c0 2收敛数列一定有界,但有界数列不一定收敛。 3.收敛数列的轻限有的可以到堕的不能达到。 不存任 例如,常数列可以达到它的极限,但一般数列 都不能达到它们的极限。 im2-0a,-≠0 n-→on n 井
1.数列的收敛与否与这个数列的增减性无关 常数列一定是收敛数列。 # lim n C C → = [几点说明] 2.收敛数列一定有界,但有界数列不一定收敛。 3.收敛数列的极限有的可以达到有的不能达到。 例如,常数列可以达到它的极限,但一般数列 都不能达到它们的极限。 1 lim 0 n→ n = 1 0 n a n = ( ) 1 lim 1 n n − → − 不存在
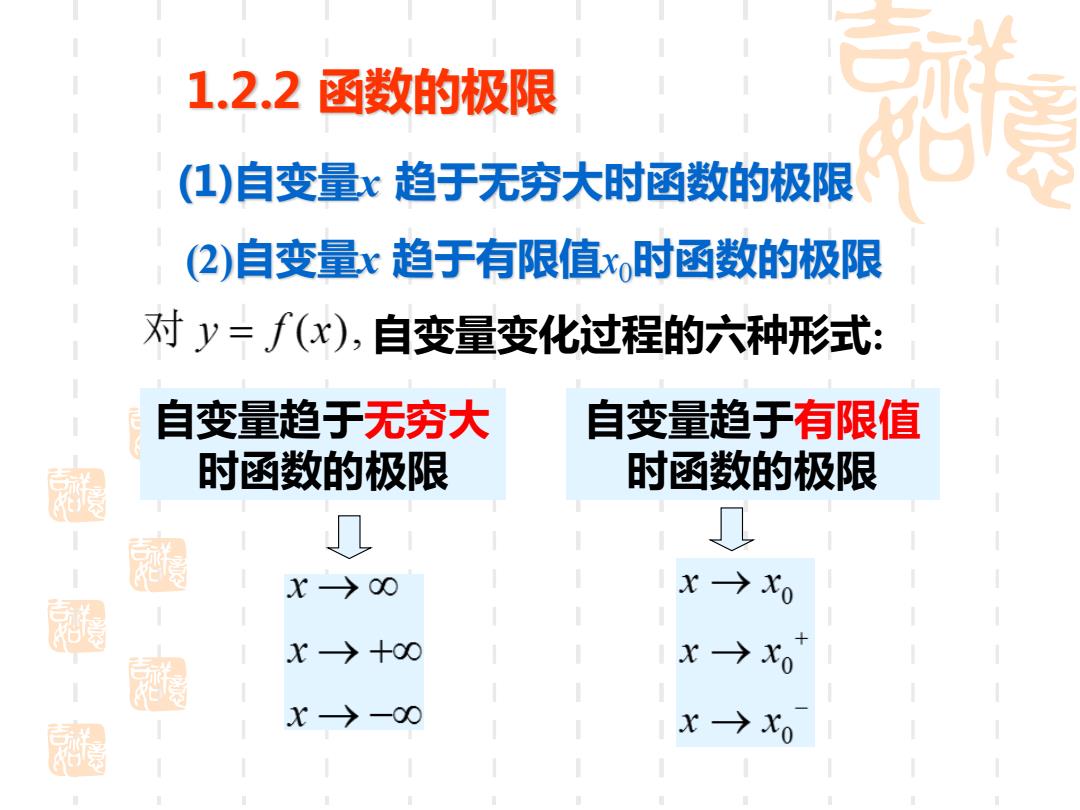
1.2.2函数的极限 (1)自变量x趋于无穷大时函数的极限 (2)自变量x趋于有限值x时函数的极限 对y=∫(x),自变量变化过程的六种形式: 自变量趋于无穷大 自变量趋于有限值 时函数的极限 时函数的极限 涵 X→00 x→x0 X→十00 x→xo X→一00 x→xo
1.2.2 函数的极限 (1)自变量x 趋于无穷大时函数的极限 (2)自变量x 趋于有限值x0时函数的极限 自变量趋于有限值 时函数的极限 自变量变化过程的六种形式: 自变量趋于无穷大 时函数的极限

(1)自变量x趋于无穷大时函数的极限 x→0(x→+0,x→-0) 考察函数 y= x+1 当x的绝对值趋于 履 无穷大时的变化趋势。 涵
(1)自变量x 趋于无穷大时函数的极限 考察函数 x 当x的绝对值趋于 x y +1 = 无穷大时的变化趋势
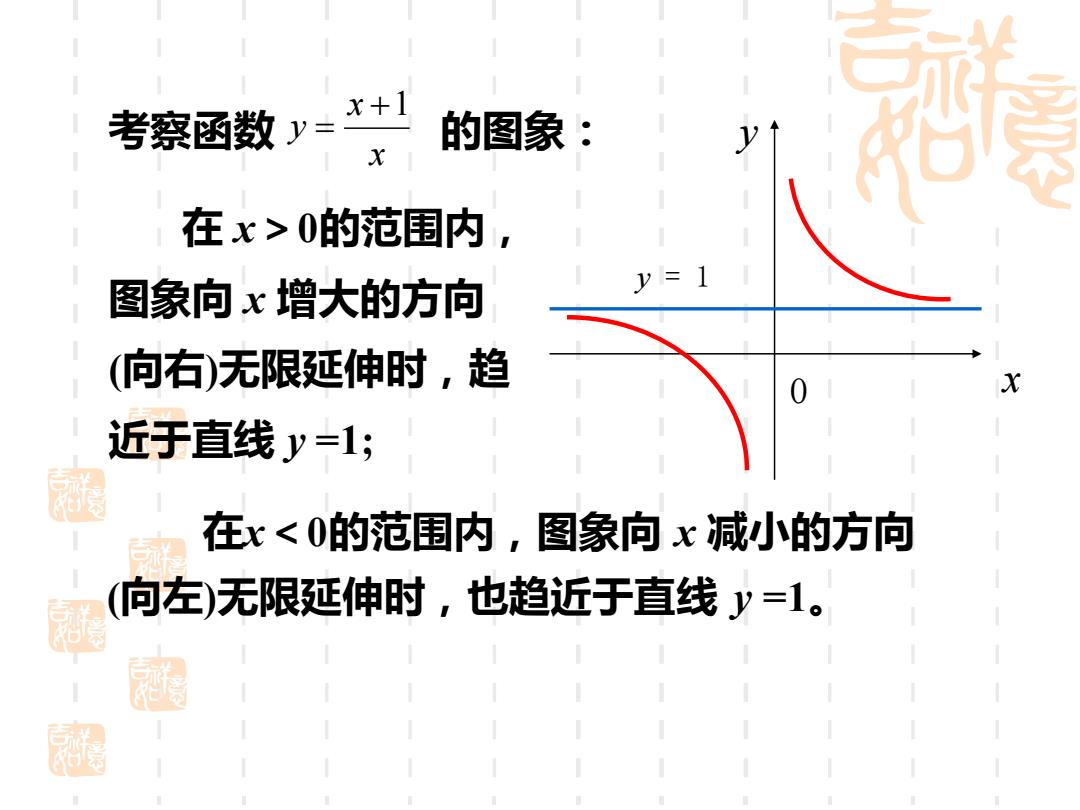
考察函数y-x+1 的图象: X 在x>0的范围内 图象向x增大的方向 y=1 (向右)无限延伸时,趋 x 近于直线y=1; 湿 在x<0的范围内,图象向x减小的方向 向左)无限延伸时,也趋近于直线y=1
在x<0的范围内,图象向 x 减小的方向 (向左)无限延伸时,也趋近于直线 y =1。 考察函数 x x y +1 = 的图象: y x y = 1 0 在 x>0的范围内, 图象向 x 增大的方向 (向右)无限延伸时,趋 近于直线 y =1;