
《医药高等数学》课程教学大纲 (执笔人:高健审核人:刘国旗教学院长:肖锦铖) 课程简介 (一)课程代码: (二)课程名称: 医药高等数学(Medical Advanced Mathematics) (三)课程类别: 专业基础课程 (四)修读对象: 生物医学工程本科专业学生 (五)总学时与学分: 总学时45学时,理论45学时。学分:2.5 (六)相关课程: 先修课程:高等数学。后续课程: (七)内容提要: 医药高等数学是高等学校医药类本科各专业学生的一门必修的重要基础理论课, 对于提高学习能力,培养科学素养,锻炼创新能力都有很重要的支撑作用。主要内容 有函数、极限与连续,一元函数微积分,常微分方程等基础内容。这些内容不仅在现 代医学科学中有许多重要应用,而且是学习其他数学方法,尤其是钻研医学生物科学 必须具备的基础。 二、教学目的和教学方法 通过医药高等数学课程的学习,使学生掌握高等数学的基本概念、基本理论和基 本运算技能,为后续课程的学习奠定必要的数学基础。 通过医药高等数学的整个教学过程,逐渐培养学生的抽象概括问题的能力、逻辑 推理能力、空间想象能力、自学能力以及创新能力,并使他(她)们具有比较熟练的 运算能力和综合运用数学方法去分析问题、解决问题的能力。 1
1 《医药高等数学》课程教学大纲 (执笔人:高健 审核人: 刘国旗 教学院长: 肖锦铖 ) 一、 课程简介 (一)课程代码: (二)课程名称: 医药高等数学 ( Medical Advanced Mathematics) (三)课程类别: 专业基础课程 (四)修读对象: 生物医学工程本科专业学生 (五)总学时与学分: 总学时 45 学时,理论 45 学时。学分:2.5 (六)相关课程: 先修课程:高等数学。后续课程: (七)内容提要: 医药高等数学是高等学校医药类本科各专业学生的一门必修的重要基础理论课, 对于提高学习能力,培养科学素养,锻炼创新能力都有很重要的支撑作用。主要内容 有函数、极限与连续,一元函数微积分,常微分方程等基础内容。这些内容不仅在现 代医学科学中有许多重要应用,而且是学习其他数学方法,尤其是钻研医学生物科学 必须具备的基础。 二、教学目的和教学方法 通过医药高等数学课程的学习,使学生掌握高等数学的基本概念、基本理论和基 本运算技能,为后续课程的学习奠定必要的数学基础。 通过医药高等数学的整个教学过程,逐渐培养学生的抽象概括问题的能力、逻辑 推理能力、空间想象能力、自学能力以及创新能力,并使他(她)们具有比较熟练的 运算能力和综合运用数学方法去分析问题、解决问题的能力
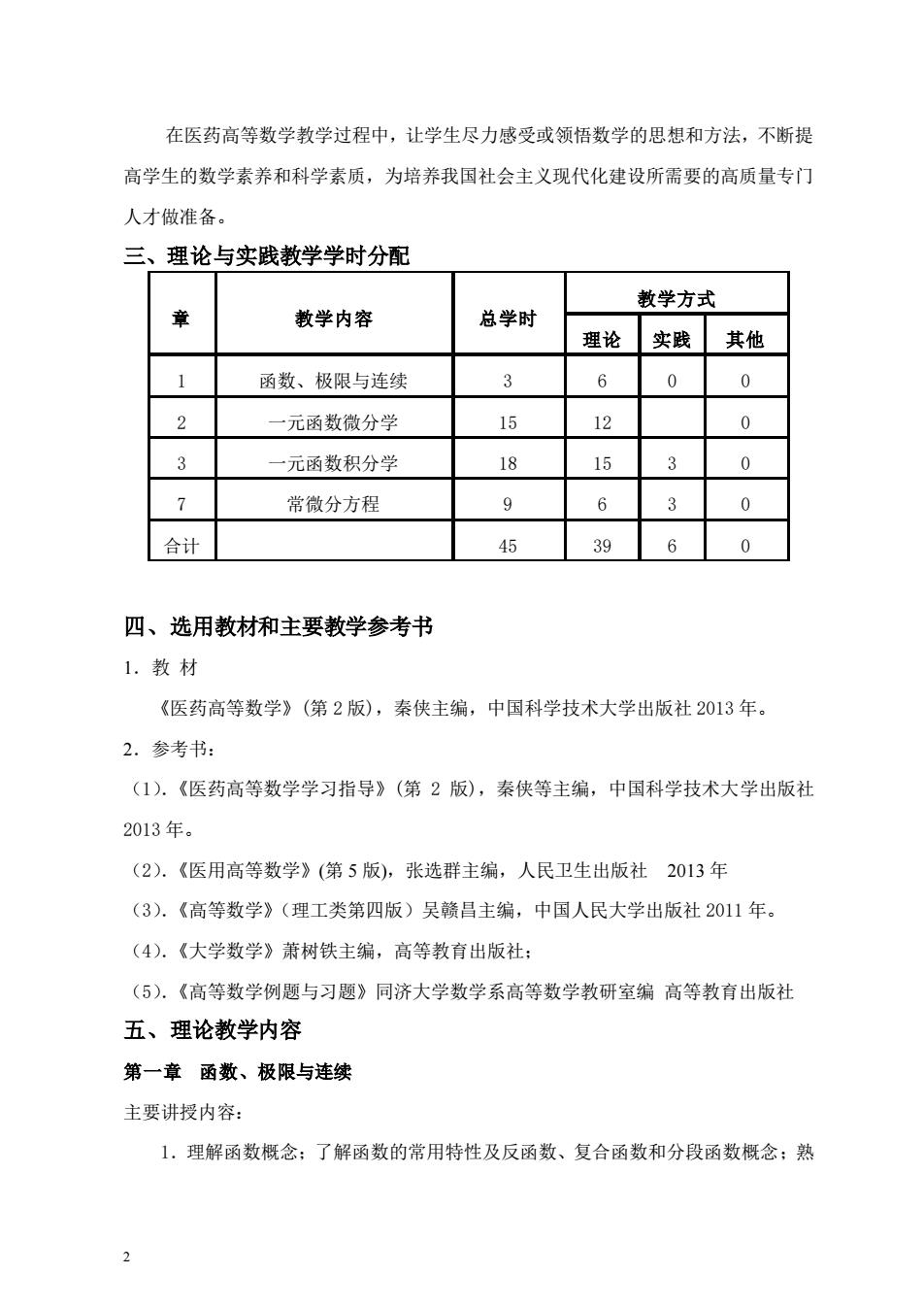
在医药高等数学教学过程中,让学生尽力感受或领悟数学的思想和方法,不断提 高学生的数学素养和科学素质,为培养我国社会主义现代化建设所需要的高质量专门 人才做准备。 三、理论与实践教学学时分配 教学方式 章 教学内容 总学时 理论 实践 其他 1 函数、极限与连续 3 6 0 0 2 一元函数微分学 15 12 0 3 一元函数积分学 18 15 3 0 7 常微分方程 9 6 3 0 合计 45 39 6 0 四、选用教材和主要教学参考书 1.教材 《医药高等数学》(第2版),秦侠主编,中国科学技术大学出版社2013年。 2.参考书: (1).《医药高等数学学习指导》(第2版),秦侠等主编,中国科学技术大学出版社 2013年。 (2).《医用高等数学》(第5版),张选群主编,人民卫生出版社2013年 (3).《高等数学》(理工类第四版)吴赣昌主编,中国人民大学出版社2011年。 (4).《大学数学》萧树铁主编,高等教育出版社: (5).《高等数学例题与习题》同济大学数学系高等数学教研室编高等教育出版社 五、理论教学内容 第一章函数、极限与连续 主要讲授内容: 1.理解函数概念;了解函数的常用特性及反函数、复合函数和分段函数概念;熟 2
2 在医药高等数学教学过程中,让学生尽力感受或领悟数学的思想和方法,不断提 高学生的数学素养和科学素质,为培养我国社会主义现代化建设所需要的高质量专门 人才做准备。 三、理论与实践教学学时分配 章 教学内容 总学时 教学方式 理论 实践 其他 1 函数、极限与连续 3 6 0 0 2 一元函数微分学 15 12 0 3 一元函数积分学 18 15 3 0 7 常微分方程 9 6 3 0 合计 45 39 6 0 四、选用教材和主要教学参考书 1.教 材 《医药高等数学》(第 2 版),秦侠主编,中国科学技术大学出版社 2013 年。 2.参考书: (1).《医药高等数学学习指导》(第 2 版),秦侠等主编,中国科学技术大学出版社 2013 年。 (2).《医用高等数学》(第 5 版),张选群主编,人民卫生出版社 2013 年 (3).《高等数学》(理工类第四版)吴赣昌主编,中国人民大学出版社 2011 年。 (4).《大学数学》萧树铁主编,高等教育出版社; (5).《高等数学例题与习题》同济大学数学系高等数学教研室编 高等教育出版社 五、理论教学内容 第一章 函数、极限与连续 主要讲授内容: 1.理解函数概念;了解函数的常用特性及反函数、复合函数和分段函数概念;熟

悉基本初算函数及其性质与图形:会建立出简单实际问题的函数表达式。 2.了解数列及函数极限的概念:理解极限与单侧极限的关系:掌握极限的四则运 算法则和极限存在准则,会用重要极限求有关极限:理解无穷小、无穷大概念和有关 性质,掌握无穷小的比较方法。 3.理解函数在一点的连续概念,会判断间断点的类型;了解初等函数的连续性和 闭区间上连续函数性质。 教学时数:6学时 重点与难点: 教学重点是有关求极限的方法:教学难点是极限的定义。 思考题或练习题: 本章课后练习题数量的大约三分之二。 第二章一元函数微分学 主要讲授内容: 1.理解导数与微分概念,了解导数与微分的几何意义及可微、可导与连续性之间 的关系;会用导数描述某些物理量。 2.熟悉导数运算法则、求导基本公式:了解高阶导数概念,能熟练计算初等函数 的一、二阶导数。 3.熟悉微分运算法则,能熟练计算一阶微分,了解一阶微分形式不变性,会用 微分作近似计算。 4.理解Role定理和Lagrange中值定理;会利用中值定理证明一些较为简单的数 学问题。 4.掌握Hospital求极限法则: 5.理解极值概念:掌握求函数极值的方法;会求最值及简单应用问题。 6.掌握利用导数判断函数单调性的方法:会描绘函数的图形(凹凸性、拐点、 渐近线)。 教学时数:15学时 3
3 悉基本初算函数及其性质与图形;会建立出简单实际问题的函数表达式。 2.了解数列及函数极限的概念;理解极限与单侧极限的关系;掌握极限的四则运 算法则和极限存在准则,会用重要极限求有关极限;理解无穷小、无穷大概念和有关 性质,掌握无穷小的比较方法。 3.理解函数在一点的连续概念,会判断间断点的类型;了解初等函数的连续性和 闭区间上连续函数性质。 教学时数:6 学时 重点与难点: 教学重点是有关求极限的方法;教学难点是极限的定义。 思考题或练习题: 本章课后练习题数量的大约三分之二。 第二章 一元函数微分学 主要讲授内容: 1.理解导数与微分概念,了解导数与微分的几何意义及可微、可导与连续性之间 的关系;会用导数描述某些物理量。 2.熟悉导数运算法则、求导基本公式;了解高阶导数概念,能熟练计算初等函数 的一、二阶导数。 3.熟悉微分运算法则,能熟练计算一阶微分,了解一阶微分形式不变性,会用 微分作近似计算。 4.理解 Rolle 定理和 Lagrange 中值定理;会利用中值定理证明一些较为简单的数 学问题。 4.掌握 L'Hospital 求极限法则; 5.理解极值概念;掌握求函数极值的方法;会求最值及简单应用问题。 6.掌握利用导数判断函数单调性的方法;会描绘函数的图形(凹凸性、拐点、 渐近线)。 教学时数:15 学时

重点与难点: 教学重点:导数与微分概念的几何意义及求导法则、Lagrange中值定理和 L'Hospital求极限法则及用导数研究函数的性态。教学难点是复合函数求导、隐函数求 导;L心Hospital法则及导数的应用。 思考题或练习题: 本章课后练习题数量的大约三分之二。 第三章一元函数积分学 主要讲授内容: 1.理解原函数、不定积分概念,熟悉不定积分性质及基本公式:掌握用换元法及 分部积分法计算有关函数的不定积分。 2.理解定积分概念及性质;认识变上限的定积分函数及其求导公式;熟悉 Newton-Leibni立公式:掌握用换元法及分部积分法计算有关函数的定积分。 3.了解两种类型的反常积分概念,会判断简单的广义积分的收敛性问题。 4.掌握用定积分(微元法)表达和计算一些几何量(面积、某些体积、弧长等)。 教学时数:18学时 重点与难点: 教学重点:不定积分性质及运算,积分法的熟练运用;定积分性质与微积分学基本 定理、Newton-Leibniz公式及定积分的计算。实际问题的定积分(微元法)表达。 教学难点是掌握用换元法及分部积分法计算有关函数的不定积分。反常积分的理解与 运用。定积分在几何和医药方面的应用。 思考题或练习题: 本章课后练习题数量的大约三分之二。 第七章常微分方程 主要讲授内容: 1.了解常微分方程、通解、初始条件和特解等基本概念:会识别微分方程的类型。 2.掌握可分离变量方程、齐次方程、一阶线性方程的求解方法: 4
4 重点与难点: 教学重点:导数与微分概念的几何意义及求导法则、Lagrange 中值定理和 L'Hospital 求极限法则及用导数研究函数的性态。教学难点是复合函数求导、隐函数求 导; L'Hospital 法则及导数的应用。 思考题或练习题: 本章课后练习题数量的大约三分之二。 第三章 一元函数积分学 主要讲授内容: 1.理解原函数、不定积分概念,熟悉不定积分性质及基本公式;掌握用换元法及 分部积分法计算有关函数的不定积分。 2. 理解定积分概念及性质;认识变上限的定积分函数及其求导公式;熟悉 Newton −Leibniz 公式;掌握用换元法及分部积分法计算有关函数的定积分。 3.了解两种类型的反常积分概念,会判断简单的广义积分的收敛性问题。。 4. 掌握用定积分(微元法)表达和计算一些几何量(面积、某些体积、弧长等)。 教学时数:18 学时 重点与难点: 教学重点:不定积分性质及运算,积分法的熟练运用;定积分性质与微积分学基本 定理、 Newton −Leibniz 公式及定积分的计算。实际问题的定积分(微元法)表达。 教学难点是掌握用换元法及分部积分法计算有关函数的不定积分。反常积分的理解与 运用。定积分在几何和医药方面的应用。 思考题或练习题: 本章课后练习题数量的大约三分之二。 第七章 常微分方程 主要讲授内容: 1. 了解常微分方程、通解、初始条件和特解等基本概念;会识别微分方程的类型。 2.掌握可分离变量方程、齐次方程、一阶线性方程的求解方法;

3.会用降阶法解几种特殊的高阶方程: 4.掌握二阶常系数线性齐次方程的求解。 教学时数:9学时 重点与难点: 教学重点:变量分离方程、一阶线性方程的求解方法和二阶常系数线性齐次方程 的求解。教学难点:常数变异法。 思考题或练习题: 本章课后练习题数量的大约三分之二。 六、实验(见习)教学内容与要求 第一次实验内容是积分思想与方法的总结,通过单元的综合练习题,让学生到黑 板演练,第二次实验内容是微分方程的应用,通过本章或前面章节的复习题,让学生自 己演练。也可由教师根据学生掌握情况自行选定,要基本覆盖全章的主要内容,重点 是概念识别、处理问题的方法,淡化技巧性操作。 七、考核方式及要求 考核方式:闭卷考试。采取统一命题、统一阅卷。主要考查基础知识、分析能力、 计算能力。试题类型多样化:选择、填空、计算、解答、应用等:建议试题难度分布 如下:基本题50%、中等题30%、较难题15%、难题5%. 成绩评定:期末考试(闭卷)占总成绩的70%,平时成绩占30%。课堂讨论占平时 成绩的25%,出勤与作业占平时成绩的25%,测验和小论文占平时成绩的50%。注: 平时成绩包括课堂讨论、作业、测验、小论文等。 修订日期:2014年3月18日 5
5 3.会用降阶法解几种特殊的高阶方程; 4. 掌握二阶常系数线性齐次方程的求解。 教学时数:9 学时 重点与难点: 教学重点:变量分离方程、一阶线性方程的求解方法和二阶常系数线性齐次方程 的求解。教学难点:常数变异法。 思考题或练习题: 本章课后练习题数量的大约三分之二。 六、实验(见习)教学内容与要求 第一次实验内容是积分思想与方法的总结,通过单元的综合练习题,让学生到黑 板演练,第二次实验内容是微分方程的应用,通过本章或前面章节的复习题,让学生自 己演练。也可由教师根据学生掌握情况自行选定,要基本覆盖全章的主要内容,重点 是概念识别、处理问题的方法,淡化技巧性操作。 七、考核方式及要求 考核方式:闭卷考试。采取统一命题、统一阅卷。主要考查基础知识、分析能力、 计算能力。试题类型多样化:选择、填空、计算、解答、应用等;建议试题难度分布 如下:基本题 50%、中等题 30%、较难题 15%、难题 5%. 成绩评定:期末考试(闭卷)占总成绩的 70%,平时成绩占 30%。课堂讨论占平时 成绩的 25%,出勤与作业占平时成绩的 25%,测验和小论文占平时成绩的 50%。注: 平时成绩包括课堂讨论、作业、测验、小论文等。 修订日期:2014 年 3 月 18 日