第4章随机变量的数学特征 4.1内容框图 数字特征 数学期望 方差 矩 协方差 相关系数 重要分布的期望和方差 4.2基本要求 (1)理解数学期望、方差的概念,掌握它们的性质与计算 (2)熟记二项分布、普阿松分布、正态分布、均匀分布、指数分布的数学期望和方差 (3)会算随机变量函数的数学期望 (4)了解矩、协方差与相关系数的概念、性质和计算 4.3内容概要 1)一维随机变量的数学期望 设5是离散型随机变量,概率分布为P{5=x,}(i=1,2,…)。当级数 ExP=x 绝对收敛时,称∑x,P5=x}为5的数学期望,记为E5或E(⑤),即 E6-xPx i=1 若∑x,P传=x}发散,则称5的数学期望不存在
第 4 章 随机变量的数学特征 4.1 内容框图 4.2 基本要求 (1) 理解数学期望、方差的概念,掌握它们的性质与计算. (2) 熟记二项分布、普阿松分布、正态分布、均匀分布、指数分布的数学期望和方差. (3) 会算随机变量函数的数学期望. (4) 了解矩、协方差与相关系数的概念、性质和计算. 4.3 内容概要 1) 一维随机变量的数学期望 设 是离散型随机变量,概率分布为 { }i P = x ( i = 1, 2, )。当级数 = = 1 { } i i i x P x 绝对收敛时,称 = = 1 { } i i i x P x 为 的数学期望,记为 E 或 E( ) ,即 E = = = 1 { } i i i x P x 。 若 = = 1 { } i i i x P x 发散,则称 的数学期望不存在。 数字特征 数学期望 方差 矩 协方差 相关系数 重要分布的期望和方差

设5是连续型随机变量,概率窑度为p()。当x(xtr绝对收敛时,称 口xp(x)dr为5的数学期量,记为E5,即 Exp(x)dx. 若(x)dr发散,则称5的数学期望不存在。 2)随机变量函数的数学期望 设7为随机变量5的函数,即刀=f(5),其中f为连续的实值函数。 (1)若5为离散型随机变量,概率分布为P{5=x,}(i=1,2,…),则当 三化PG=绝对收敏时,有 En=f(5)= 2fx,)P5=x. (2)若5为连续型随机变量,概率密度为(x),则当广f(x)p(x)d绝对收敛时,有 En=Ef()=f(x)(x)dx. 3)数学期望的性质 (1) 若5是随机变量,b,c是常量,则E(b5+c)=bE5+c。 推论1若c是常量,则Ec=c。 推论2若5是随机变量,c是常量,则E(5+c)=E5+c。 推论3若5是随机变量,c是常量,则E(c)=cE5。 (2)若f()和g(5)都是随机变量5的函数,则ELf(5)±g(5】=Ef()±Eg(5). (3) 若随机变量5的取值落在常量α,b之间,则其数学期望也必落在α,b之间,即 若a≤5≤b,则a≤E5≤b。 4)一维随机变量的方差 若E(5-E)存在,称它为随机变量5的方差,记为D5或Var(5),即
2 设 是连续型随机变量,概率密度为 (x) 。当 + − x(x)dx 绝对收敛时,称 + − x(x)dx 为 的数学期望,记为 E ,即 E = + − x(x)dx 。 若 + − x(x)dx 发散,则称 的数学期望不存在。 2) 随机变量函数的数学期望 设 为随机变量 的函数,即 = f ( ) ,其中 f 为连续的实值函数。 ( 1 ) 若 为离散型随机变量,概率分布为 { }i P = x ( i = 1, 2, ) ,则当 = = 1 ( ) { } i i i f x P x 绝对收敛时,有 E = Ef ( ) = = = 1 ( ) { } i i i f x P x 。 (2)若 为连续型随机变量,概率密度为 (x) ,则当 + − f (x)(x)dx 绝对收敛时,有 E = Ef ( ) = + − f (x)(x)dx 。 3) 数学期望的性质 (1) 若 是随机变量, b,c 是常量,则 E(b + c) = bE + c 。 推论 1 若 c 是常量,则 Ec = c 。 推论 2 若 是随机变量, c 是常量,则 E( + c) = E + c 。 推论 3 若 是随机变量, c 是常量,则 E(c ) = cE 。 (.2) 若 f () 和 g() 都是随机变量 的函数,则 E[ f ( ) g( )] = Ef ( ) Eg( ) . (.3) 若随机变量 的取值落在常量 a,b 之间,则其数学期望也必落在 a,b 之间,即 若 a b ,则 a E b 。 4) 一维随机变量的方差 若 2 E( − E ) 存在,称它为随机变量 的方差,记为 D 或 Var( ) ,即

D5=E(5-E5)2。 方差的正的平方根√D5,称为标准差或均方差,记为O:,即 0=DE 。 随机变量5的方差可由下列公式求出: D5=E52-(E5)2。 5)方差的性质 ()若5是随机变量,b,c是常量,则D(b5+c)=b2D5。 推论1若c是常量,则Dc=0。 推论2若5是随机变量,c是常量,则D(5+c)=D5。 推论3若5是随机变量,c是常量,则D(c)=c2D5。 设随机变量5的均值为E5,方差为D5,称*=5一E延为5的标准化随机变量。求 DE 5*的数学期望E5*和方差DE*。 (2)若5是随机变量,c是任意常量,则D5≤E(5-c)2。当且仅当c=E5时, E(5-c)2达到最小值D5。 (3)切比雪夫(9m6 LlweB)不等式 对于任何具有有限方差的随机变量5,都有P5-B5引上≤,其中G是红- 正数。 (4)如果随机变量5的方差为零,则随机变量5以概率1取值为E5。即如果D5=0, 则有 P{5=E5}=1。 6)一维随机变量的矩 称E(ξ“)为随机变量5的k阶原点矩,简称k阶矩。称E(ξ-E)为随机变量5 的k阶中心矩。 显然:1阶原点矩就是数学期望E5:2阶中心矩E(E-EE)2就是方差D5
3 D = 2 E( − E ) 。 方差的正的平方根 D ,称为标准差或均方差,记为 ,即 = D 。 随机变量 的方差可由下列公式求出: D = 2 2 E − (E) 。 5) 方差的性质 (1) 若 是随机变量, b,c 是常量,则 D b c b D 2 ( + ) = 。 推论 1 若 c 是常量,则 Dc = 0 。 推论 2 若 是随机变量, c 是常量,则 D( + c) = D 。 推论 3 若 是随机变量, c 是常量,则 D c c D 2 ( ) = 。 设随机变量 的均值为 E ,方差为 D ,称 D − E * = 为 的标准化随机变量。求 * 的数学期望 E * 和方差 D *。 (2) 若 是随机变量, c 是任意常量,则 2 D E( − c) 。当且仅当 c = E 时, 2 E( − c) 达到最小值 D 。 (3)切比雪夫(Чибышев)不等式 对于任何具有有限方差的随机变量 ,都有 2 { } D P − E ,其中 是任一 正数。 (4) 如果随机变量 的方差为零,则随机变量 以概率 1 取值为 E 。即如果 D = 0 , 则有 P{ = E} = 1。 6)一维随机变量的矩 称 ( ) k E 为随机变量 的 k 阶原点矩,简称 k 阶矩。称 k E( − E ) 为随机变量 的 k 阶中心矩。 显然:1 阶原点矩就是数学期望 E ;2 阶中心矩 2 E( − E ) 就是方差 D
7)一些常用分布的数学期望和方差 表1常用离散型和连续型分布 分布 分布 数学 概率分布或概率密度 名称 记号 期望 方差 0-1 P=k)=p(1-p)-k 分布 b(1,p) p p(1-p) k=0,1 二项 P{5=k}=Cp*I-p)"- np 分布 b(n,p) np(1-p) k=0,1,…,n 普阿松 P() 君e 分布 k=012,… 几何 P=k)=(1-p)p 分布 g(p) k=1,2,… 学 P{5=k}= ChC 超几何 H(n,M,N) C nM 分布 N N N-1 k=0,1,…,n 1 均匀 U(a,b) a≤x≤b a+b (b-a)2 分布 p(x)=3b-a 0 其它 2 12 指数 Ae-ix x>0 E(1) p(x)= 分布 0 x≤0 1-元 是 正态 分布 N(4,o2) p(x)= e 62 V2元 4
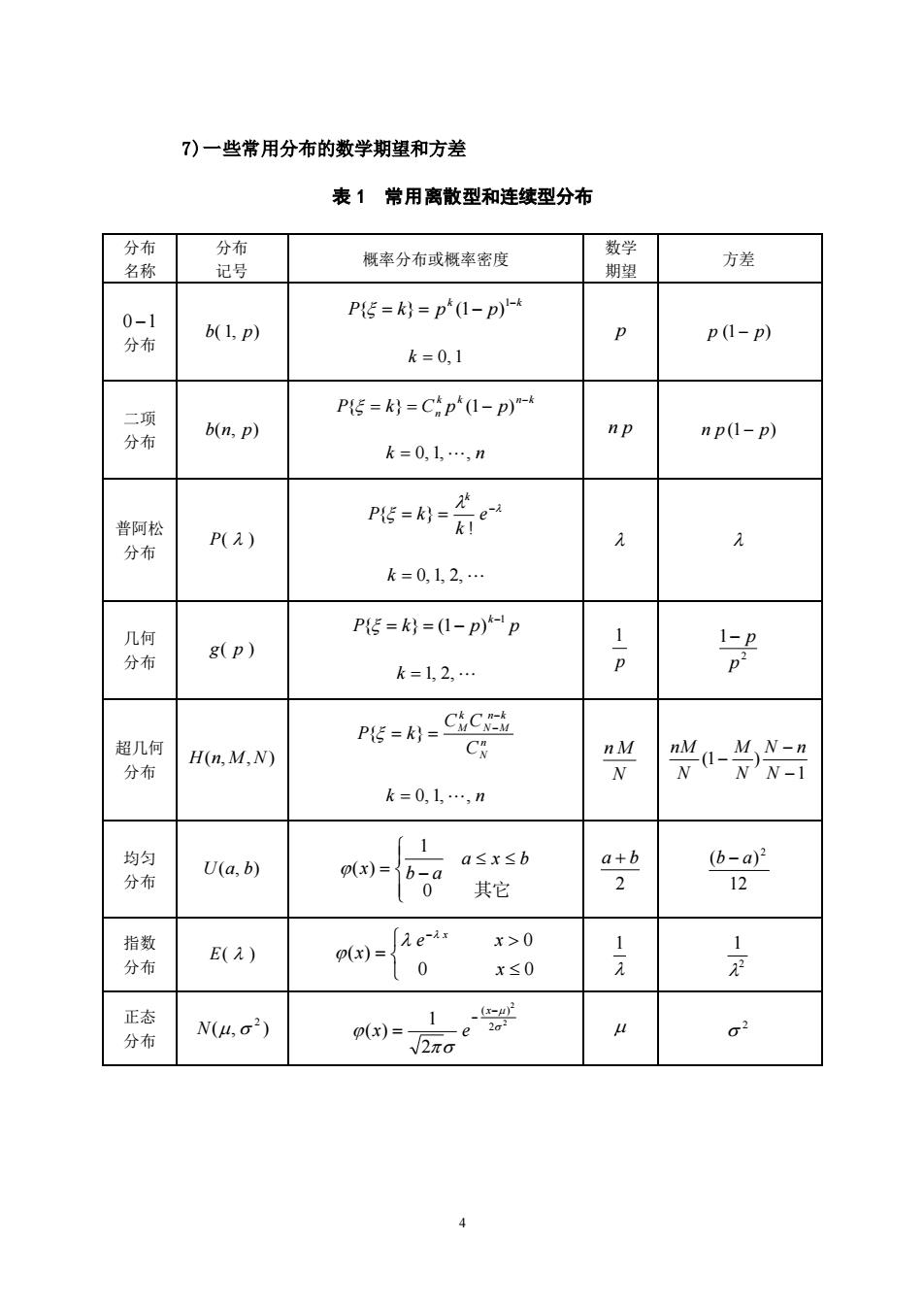
4 7)一些常用分布的数学期望和方差 表 1 常用离散型和连续型分布 分布 名称 分布 记号 概率分布或概率密度 数学 期望 方差 0 −1 分布 b( 1, p) k k P k p p − = = − 1 { } (1 ) k = 0, 1 p p (1− p) 二项 分布 b(n, p) k k n k P k Cn p p − { = } = (1− ) k = 0, 1, , n n p n p (1− p) 普阿松 分布 P( ) − = = e k P k k ! { } k = 0, 1, 2, 几何 分布 g( p ) P k p p k 1 { } (1 ) − = = − k = 1, 2, p 1 2 1 p − p 超几何 分布 H(n, M , N) n N n k N M k M C C C P k − − { = } = k = 0, 1, , n N n M 1 (1 ) − − − N N n N M N nM 均匀 分布 U(a, b) = − 0 其它 1 ( ) a x b x b a 2 a + b 12 ( ) 2 b − a 指数 分布 E( ) = − 0 0 0 ( ) x e x x x 1 2 1 正态 分布 ( , ) 2 N 2 2 2 ( ) 2 1 ( ) − − = x x e 2

e月 x>0 x2 x2(n) p(x)= ir 2n 分布 0 x≤0 0 1分布 p(x)= n t(n) (n>1) (n>2) nπr n n-2 2 雕”-1 2n2(m+n-2) m2n2x2 x>0 n F分布 F(m,n) r%r(哈omx+m7 十打 n-2 m(n-2)2(n-4) p(x)= 2 (n>2) 0 x≤0 (n>4) 8) 二维随机变量的数学期望 二维随机变量函数的数学期望 设f(5,)是5,n的函数,f(5,)的数学期望记为Ef(5,7)。 (1)如果(5,7)为二维离散型随机变量,联合概率分布为 P{5=x,7=y}(i,j=1,2,…), 则当22,y)P5=,刀=,绝对收数时,有 Ef(5,)= 221x,y,)PE=x,0=y i=l jal (2)如果(5,η)为二维连续型随机变量,联合概率密度为 p(x,y),-0<x<+0,-0<y<+0, 则当fx,ypx,y绝对收敛时,有 Ef作,n)=fxox,yd。 二维随机变量中5,门各自的数学期望和方差 (1)把5,),52,72看作f(5,)的特殊情形,用求Ef(5,)的公式求出E5,En, J
5 2 分布 ( ) 2 n = − − 0 0 0 ) 2 2 ( 1 ( ) 2 1 2 2 x x e x n x n x n n 2n t 分布 t ( n ) 2 2 1 (1 ) ) 2 ( ) 2 1 ( ( ) + − + + = n n x n n n x 0 (n 1) n − 2 n (n 2) F 分布 F(m, n) + + = + − 0 0 0 ( ) ) 2 ) ( 2 ( ) 2 ( ( ) 2 1 2 2 2 x x mx n m n x m n m n x m n m n m n − 2 n (n 2) ( 2) ( 4) 2 ( 2) 2 2 − − + − m n n n m n (n 4) 8) 二维随机变量的数学期望 二维随机变量函数的数学期望 设 f ( ,) 是 , 的函数, f ( ,) 的数学期望记为 Ef (,) 。 (1)如果( , )为二维离散型随机变量,联合概率分布为 { , } i j P = x = y ( i, j = 1, 2, ) , 则当 = = = = 1 1 ( , ) { , } i j i j i j f x y P x y 绝对收敛时,有 Ef (,) = = = = = 1 1 ( , ) { , } i j i j i j f x y P x y 。 (2)如果( , )为二维连续型随机变量,联合概率密度为 (x, y) , − x +, − y +, 则当 + − + − f (x, y)(x, y)dxdy 绝对收敛时,有 Ef (,) = + − + − f (x, y)(x, y)dxdy 。 二维随机变量中 , 各自的数学期望和方差 (1)把 ,, 2 2 , 看作 f ( ,) 的特殊情形,用求 Ef (,) 的公式求出 E , E

E52,E72,再求出D5=E52-(E5)2,Dn=En2-(E)2。 (2)先求5,7的边缘分布,把边缘分布看作是5,7的一维分布,按照一维随机变量求 数学期望和方差的公式,求出E5,En,D5,Dn。 随机变量和差、乘积的数学期望,随机变量和差的方差 定理随机变量和差的数学期望等于它们的数学期望的和差,即 E(5±7)=E5±En。 推论n个随机变量之和的数学期望等于它们的数学期望之和,即有 定理独立随机变量乘积的数学期望等于它们的数学期望的乘积,即若5,η相互独立, 则有 E(5)=E5En。 推论n个相互独立的随机变量乘积的数学期望等于它们数学期望的乘积,即如果 51,52,…,5n相互独立,则有 i1 定理独立随机变量和差的方差等于它们的方差之和,即若5,刀相互独立,则有 D(5±)=D5+Dn。 推论n个相互独立的随机变量之和的方差等于它们的方差之和,即若51,52,…,5n相 互独立,则有 6
6 2 E , 2 E ,再求出 D 2 2 = E − (E) , D 2 2 = E − (E) 。 (2)先求 , 的边缘分布,把边缘分布看作是 , 的一维分布,按照一维随机变量求 数学期望和方差的公式,求出 E , E , D , D 。 随机变量和差、乘积的数学期望,随机变量和差的方差 定理 随机变量和差的数学期望等于它们的数学期望的和差,即 E( ) = E E 。 推论 n 个随机变量之和的数学期望等于它们的数学期望之和,即有 = = = n i i n i E i E 1 1 。 定理 独立随机变量乘积的数学期望等于它们的数学期望的乘积,即若 , 相互独立, 则有 E() = E E 。 推论 n 个相互独立的随机变量乘积的数学期望等于它们数学期望的乘积,即如果 n , , , 1 2 相互独立,则有 = n i E i 1 = = n i E i 1 。 定理 独立随机变量和差的方差等于它们的方差之和,即若 , 相互独立,则有 D( ) = D + D 。 推论 n 个相互独立的随机变量之和的方差等于它们的方差之和,即若 n , , , 1 2 相 互独立,则有 = = = n i i n i D i D 1 1

9)二维随机变量的协方差和相关系数 称E(5-E5)(η-E)为随机变量5与n的协方差,记为Cov(5,),即 Cov(5,)=E(5-E5n-En)。 称Co5,卫为随机变量5与刀的相关系数,记为P,即P知 Cov(s,n) D Dn DE Dn 从这一定义容易看出Co(5,)=D5,Cov(,)=Dn。 容易看出Cov(5,)=P√D5VD7。 性质1若5,n为随机变量,则Cov(5,)=E(5)-E5En。 性质2若5,n为随机变量,则D(5±)=D5±2Cov(5,)+Dn。 性质3若5,n为随机变量,则Cov(5,7)=Cov(7,5)。 性质4若5,n为随机变量,a,b,c,d为常量,则Cov(a5+b,c7+d)=acCov(5,) 性质5若51,52,n为随机变量,则Co(51+52,)=Co(51,)+Cov(52,7)。 性质6若P为5,n的相关系数,则P≤1。 性质7如果5与n之间有线性关系7=a5+b,其中a,b是常数,a≠0,则当a>0 时有P初=1,当a0; 当P--1时,5与n之间有线性关系7=a5+b,其中a,b是常数且a<0。 定义若随机变量5与7的相关系数P物=0,则称5与7不相关。 定理对随机变量5与门,下面的事实是等价的: (1)Cov(5,7)=0: (2)P=0,即5与7不相关; (3)E(5)=E5En;
7 9)二维随机变量的协方差和相关系数 称 E( − E )( − E) 为随机变量 与 的协方差,记为 Cov( ,) ,即 Cov( ,) = E( − E )( − E) 。 称 D D Cov( , ) 为随机变量 与 的相关系数,记为 ,即 = D D Cov( , ) 。 从这一定义容易看出 Cov(, ) = D ,Cov(,) = D 。 容易看出 Cov( ,) = D D 。 性质 1 若 , 为随机变量,则 Cov( ,) = E() − E E 。 性质 2 若 , 为随机变量,则 D( ) = D 2Cov(,) + D 。 性质 3 若 , 为随机变量,则 Cov( ,) =Cov(, ) 。 性质 4 若 , 为随机变量, a,b,c, d 为常量,则 Cov(a + b,c + d) = acCov(,) 性质 5 若 1 , 2 , 为随机变量,则 ( , ) Cov 1 + 2 ( , ) ( , ) = Cov 1 +Cov 2 。 性质 6 若 为 , 的相关系数,则 1。 性质 7 如果 与 之间有线性关系 = a + b ,其中 a,b 是常数, a 0 ,则当 a 0 时有 = 1 ,当 a 0 时有 = −1 。 反之,当 = 1 时, 与 之间有线性关系 = a + b ,其中 a,b 是常数且 a 0 ; 当 = −1 时, 与 之间有线性关系 = a + b ,其中 a,b 是常数且 a 0。 定义 若随机变量 与 的相关系数 = 0 ,则称 与 不相关。 定理 对随机变量 与 ,下面的事实是等价的: (1) Cov(,) = 0 ; (2) = 0 ,即 与 不相关; (3) E() = E E ;

(4)D(5±)=D5+Dn。 定理若5,7相互独立,则5与7不相关。 4.4自测题四 一、判断题:(正确打+,错误打-) 1.设离散型随机变量5的概率分布为: -1 0 8 0.4 0.4 且E5=0.2,则a=3,b=0.2。 1357 2.己知随机变量5只能取-1、0、1、2四个值,其相应的概率依次为 2C`4C`8C`16C 则5的数学期望为16/37。 Ax 00 7.已知5的分布为F(x)= xso' 则D5=1/4。 0 8.设随机变量X的概率分布为P(X=k)=a k=0,12,,其中6>0是已知常数, 2k 则D5=2。 9.设5U(0,6),7= 1,5≤4 05>4,则n的数学期望E7=23
8 (4) D( ) = D + D 。 定理 若 , 相互独立,则 与 不相关。 4.4 自测题四 一、 判断题:(正确打+,错误打-) 1.设离散型随机变量 的概率分布为: -1 0 a P 0.4 0.4 b 且 E =0.2,则 a b = = 3, 0.2。 2.已知随机变量 只能取-1、0、1、2 四个值,其相应的概率依次为 1 2C 、 3 5 4 8 16 C C C 7 、 、 , 则 的数学期望为 16/37。 3.已知随机变量 的概率密度 0 1 ( ) 0 Ax x x = 其他 ,则 E =1。 4.一袋中有 5 只乒乓球,编号为 1,2,3,4,5。现从中任取 3 只,求取出的 3 只乒乓球的最大 编号的数学期望为 4.5。 5.已知二项分布的均值为 60,方差为 20,试验次数 n ,成功的概率为 p =1/3 6. 设 X 的概率分布是: X -1 0 1 2 P(X = k) 1/5 1/2 1/5 1/10 则 E(5X+2)=3。 7. 已知 的分布为 2 0 ( ) , 0 0 x A Be x F x x − + = 则 D =1/4。 8.设随机变量 X 的概率分布为 2 ( ) , 0,1,2, ! k P X k a k k = = = …,其中 b, 0 是已知常数, 则 D = 2 。 9.设 ~U(0,6) , = 0 4 1, 4 ,则 的数学期望 E =2/3

10.设X~N(2,1),Y~N(-1,1),且X与Y相互独立,令Z=3X-2Y-6,则 Z~N(2,13). 11·设随机变量5,)独立,且其概率密度分别为f(x)= exx≥0 10x0 3.己知5的分布为F(x)= 0 x≤0' 则E5=()。 (A)1/2: (B)1: (C)2: (D)4. 4.己知随机变量X~b(n,p),且E(X)=2.4,D(X)=1.44,则二项分布的参数n,p的 值分别为()。 (A)n=4,p=0.6;(B)n=6,p=0.4: (C)n=8,p=0.3;(D)n=24,p=01. 9
9 10.设 X ~ N(2,1) ,Y ~ N(−1, 1) ,且 X 与 Y 相互独立,令 Z = 3X − 2Y − 6 ,则 Z ~ N(2, 13) . 11 .设随机变量 , 独 立 , 且 其 概 率 密 度 分 别 为 0 ( ) 0 0 x e x f x x − = , 1 0 4 ( ) 4 0 y f y = 其他 ,则, E( ) = 2。 12.两随机变量独立必不相关。 13.两随机变量 , 满足 Cov(2 +3,3 −5) = 6Cov(,) . 14.已知随机变量 , 满足 E E D D 2, 2, 1, 4, 0.5, = − = = = = − 用切比雪夫不等 式估计 P{ 6} + 1/12. 15.设随机变量 ~ P(2)泊松分布, 2 3 , 1 = − = − 则 。 二、选择题: 1. 离散型随机变量 的分布函数为 0 0 0.2 0 1 ( ) 0.5 1 2 1 2 x x F x x x = ,则 E = ( ). (A)0.2; (B)0.3; (C)0.5 ; (D)1.3. 2.已知随机变量 只能取-1、0、1、2 四个值,其相应的概率依次为 c,2c,3c,4c 则 D 为 ( )。 (A)0; (B)1; (C)2 ; (D)5. 3.已知 的分布为 2 0 ( ) , 0 0 x A Be x F x x − + = 则 E =( )。 (A)1/2; (B)1; (C)2; (D)4. 4. 已知随机变量 X ~b(n, p) ,且 E(X ) = 2.4 ,D(X ) = 1.44 ,则二项分布的参数 n, p 的 值分别为( )。 (A) n = 4, p = 0.6 ;(B) n = 6, p = 0.4 ; (C) n = 8, p = 0.3 ; (D) n = 24, p = 0.1

5.已知随机变量5~p2),则三=(. D (A)0: (B)1: (C)2: (D)1. 1-4 6.设随机变量X的分布函数为F(x)= ,x21,则数学期望E(宁()。 0, x0,己 知n~N(0,1),则有() 0a=6=1:B)a= ,b=√2: 2 0a=56=-1:0)a= 之,b=-5 8.随机变量5和7相互独立,且5服从N(1,22),7服从N(1,1),则5-7服从()。 (4)N(2,52):(B)N0,5'):(C)N0,V5):(D)N(2,V5'). 9.某零件的质量5服从N(400,400),现任取40个此类零件,记其平均质量为7,则 (A)N25):(B)No,(W):(c)NO,5):D)N2,) 10.随机变量51,52,5,相互独立,气~U(0,4),52~(0,4),5~E(3),则 E(51-252+353)=()。 (A)3:(B)6: (C)9:(D)12. 11.设5,n为两个随机变量,满足D(5+)=D(5-),则()不一定成立。 (A)E(5+7)=E5+En: (B)D(5+)=D5+Dn; (C)E(n)=EEn: (D)D(n)=DDn. 12.随机变量X与Y独立同分布,记U=X+Y,V=X-Y,则U与V必()。 (A)独立;(B)不独立;(C)相关: (D)不相关. 13.若D(5+7)=D5+Dn,则()。 0
10 5.已知随机变量 ~ p() ,则 = D E ( ). (A)0; (B)1; (C)2 ; (D) . 6. 设随机变量 X 的分布函数为 − = 0, 1 1 , 1 ( ) 2 x x x A F x ,则数学期望 ) 1 ( E =( )。 (A)1; (B) A ; (C) 3 2 ; (D)2. 7. 设随机变量 的概率密度为 2 ( 2) 4 1 ( ) , 2 x x e x R + − = , = a + b ,其中 a 0 ,已 知 ~ N(0, 1) ,则有( )。 (A) , 1 2 1 a = b = ;(B) , 2 2 2 a = b = ; (C) , 1 2 1 a = b = − ;(D) , 2 2 2 a = b = − . 8.随机变量 和 相互独立,且 服从 (1,2 ) 2 N , 服从 N(1,1) ,则 − 服从( )。 ( ) (2, 5 ) 2 A N ; ( ) (0, 3 ) 2 B N ; ( ) (0, 5 ) 2 C N ; ( ) (2, 3 ) 2 D N . 9. 某零件的质量 服从 N(400,400) ,现任取 40 个此类零件,记其平均质量为 ,则 ( ). (A) ( ) 2 N 2, 5 ; (B) ( ) 2 N 0, 3 ; (C) ( ) 2 N 0, 5 ; (D) ( ) 2 N 2, 3 . 10.随机变量 1, 2 , 3 相互独立, 1 ~ (0,4), U 2 ~ (0,4) N , 3 ~ (3) E ,则 E( 1 -2 2 +3 3 )=( )。 (A) 3; (B)6; (C)9 ; (D)12. 11. 设 , 为两个随机变量,满足 D( +) = D( −) ,则( )不一定成立。 (A) E( +) = E + E ; (B) D( +) = D + D ; (C) E() = EE ; (D) D() = DD . 12. 随机变量 X 与 Y 独立同分布,记 U = X +Y ,V = X −Y ,则 U 与 V 必( )。 (A) 独立; (B) 不独立; (C) 相关; (D)不相关. 13.若 D D D ( ) + = + ,则( )