
第八章核磁共振 一、 基本原理 ,二、核磁共振仪 ÷三、化学位移 。四、自旋一自旋偶合和自旋一自旋裂分 。五、决定质子数目的方法 冬六、在农药分析中的应用
第八章 核磁共振 ❖ 一、基本原理 ❖ 二、核磁共振仪 ❖ 三、化学位移 ❖ 四、自旋-自旋偶合和自旋—自旋裂分 ❖ 五、决定质子数目的方法 ❖ 六、在农药分析中的应用

核磁共振(nuclear magnetic resonance spectroscopy),简称 NMR。 ÷1945年F.B1och和E.M.Purce11为首的两个研究小组同时独立发现核磁共 振现象,NMR的理论基础是核物理。 。核磁共振分析能够提供四种结构信息:化学位移6、偶合常数J、各种核的 信号强度比和弛豫时间。通过分析这些信息,可以了解特定原子(如1H、13C 等)的化学环境、原子个数、邻接基团的种类及分子的空间构型。 。近20年来,随着超导磁体和脉冲傅里叶变换法的普及,NMR的新方法、新技 术不断涌现,如二维核磁共振技术、差谱技术、极化转移和波谱编辑技术及 固体核磁共振技术的发展,使核磁共振的分析方法和技术不断完善,样品用 量大大减少,灵敏度大大提高。由只能测溶液试样发展到可以做固体样品, 灵敏度很低的1C和15N等核的NMR测试也已可以顺利完成。 ÷NMR可以提供多种结构信息,不破坏样品,应用很广泛。NR也可以作定量分 析,但误差校大,不能用干痕昌分析
❖ 核磁共振 (nuclear magnetic resonance spectroscopy),简称 NMR。 ❖ 1945年F.Bloch和E.M.Purcell为首的两个研究小组同时独立发现核磁共 振现象,NMR的理论基础是核物理。 ❖ 核磁共振分析能够提供四种结构信息:化学位移δ、偶合常数J、各种核的 信号强度比和弛豫时间。通过分析这些信息,可以了解特定原子(如1H、13C 等)的化学环境、原子个数、邻接基团的种类及分子的空间构型。 ❖ 近20年来,随着超导磁体和脉冲傅里叶变换法的普及,NMR的新方法、新技 术不断涌现,如二维核磁共振技术、差谱技术、极化转移和波谱编辑技术及 固体核磁共振技术的发展,使核磁共振的分析方法和技术不断完善,样品用 量大大减少,灵敏度大大提高。由只能测溶液试样发展到可以做固体样品, 灵敏度很低的13C和15N等核的NMR测试也已可以顺利完成。 ❖ NMR可以提供多种结构信息,不破坏样品,应用很广泛。NMR也可以作定量分 析,但误差较大,不能用于痕量分析

一、 基本原理 F.Bloch和E.M.Purcell对核磁共振的解释 采取了不完全相同的理论。 F.Bloch使用的是核磁感应的观点。 E.M.Purcell用量子光学中能量吸收的观点。 这两种观点都在广泛使用。 不同场合用不同的理论
F.Bloch和E.M.Purcell对核磁共振的解释 采取了不完全相同的理论。 F.Bloch使用的是核磁感应的观点。 E.M.Purcell用量子光学中能量吸收的观点。 这两种观点都在广泛使用。 不同场合用不同的理论。 一、基本原理

核磁共振谱是由具有磁矩的原子核受射频场的照射而 发生跃迁所形成的吸收光谱。 众所周知,原于核由质子和中子组成。其质子数与核 外电子数相等,亦与原子序数相等。原子质量数为质子数 和中子数之和。原子的质量数和原子序数那是偶数时,自 旋量子数为零(=0)。原子的质量数和原子序数至少有一 个为奇数时,其自旋量子数才不为零(0)。 ≠0的原子核本身的自旋运动,将产生自旋角动量(, 并使核有一个磁矩()。具有磁矩的核在静磁场H中,就 会有一定的运动和取向。除其原有的自旋运动外还会产生 围绕H的陀螺式运动即进动(见图8一1),且有自己特定的 自旋量子数
核磁共振谱是由具有磁矩的原子核受射频场的照射而 发生跃迁所形成的吸收光谱。 众所周知,原于核由质子和中子组成。其质子数与核 外电子数相等,亦与原子序数相等。原子质量数为质子数 和中子数之和。原子的质量数和原子序数那是偶数时,自 旋量子数为零(I=0)。原子的质量数和原子序数至少有一 个为奇数时,其自旋量子数才不为零(I≠0)。 I≠0的原子核本身的自旋运动,将产生自旋角动量( ), 并使核有一个磁矩( )。具有磁矩的核在静磁场H0中,就 会有一定的运动和取向。除其原有的自旋运动外还会产生 围绕H0的陀螺式运动即进动(见图8—1),且有自己特定的 自旋量子数。 P
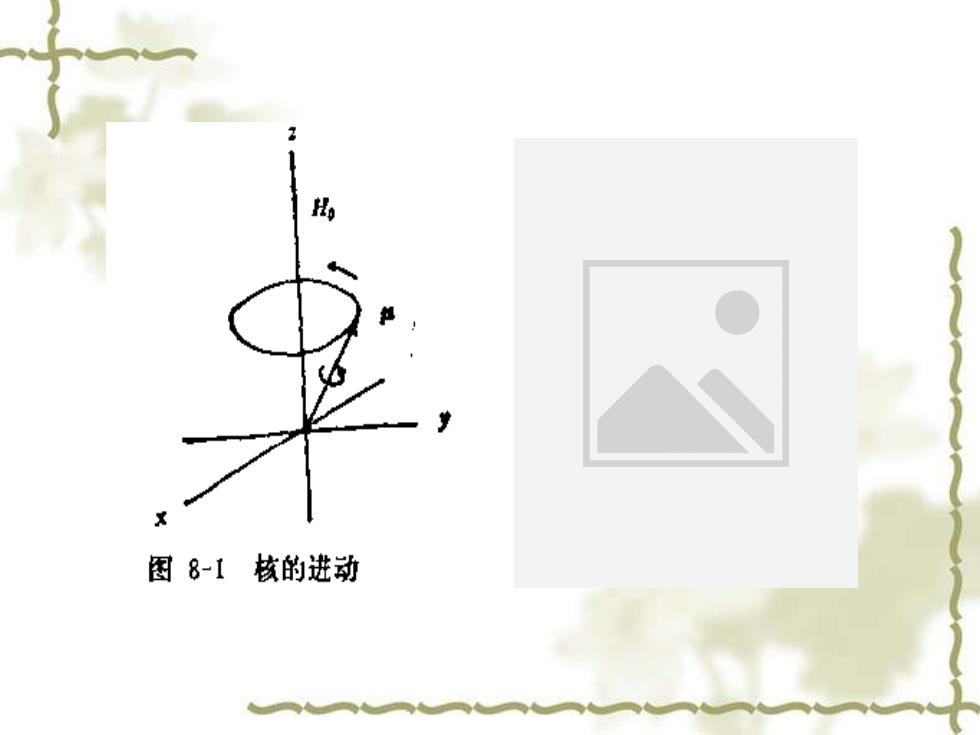
图8-1核的进动

C、10、8Si、si、s等原子核,它们的质量数和原子序数 均为偶数,自旋量子数=0。它们没有磁矩,不产生核磁 共振,因此,不能用于核磁共振研究。 H、C、N9F、Si、P等原子核,它们的质量数为奇 数,原子序数为奇数或偶数,自旋量子数=12,原子核 可看作电荷均匀分布的球体,能像陀螺一样自旋,自旋的 核具有循环的电荷,因而可产生磁场,形成磁矩,即μ0。 这类核适用于核磁共振研究。 自旋量子数>1的原子核,例如B(0=3/2),0 I=5/2),它们的质量数为奇数,原子序数为奇数或偶数: 又如:H(=1),N,B(I=1),它们的质量数为偶数, 原子序数为奇数,由于自旋核具有循环的电荷,能产生磁 场,形成磁矩,即μ0,由此都可适用于核磁共振研究。 (见表8一1)
、 、 、 、 等原子核,它们的质量数和原子序数 均为偶数,自旋量子数I=0。它们没有磁矩,不产生核磁 共振,因此,不能用于核磁共振研究。 、 、 、 、 、 等原子核,它们的质量数为奇 数,原子序数为奇数或偶数,自旋量子数I=1/2,原子核 可看作电荷均匀分布的球体,能像陀螺一样自旋,自旋的 核具有循环的电荷,因而可产生磁场,形成磁矩,即μ≠0。 这类核适用于核磁共振研究。 自旋量子数I>1的原子核,例如 (I=3/2), (I=5/2),它们的质量数为奇数,原子序数为奇数或偶数: 又如: (I=1), , (I=1),它们的质量数为偶数, 原子序数为奇数,由于自旋核具有循环的电荷,能产生磁 场,形成磁矩,即μ≠0,由此都可适用于核磁共振研究。 (见表8—1)。 12 6 C 16 8 O 28 14Si 30 14Si 30 16S 1 1 H 13 6 C 15 7 N 19 9 F 29 14Si 31 15P 11 5 B 17 8 O 2 1 H 10 5 B 14 7 N

表8-1原子的自旋量子数 原子质量数 原子序数 自旋量子数(1) 实 例 俩 绸 1=0 18C,t0,Si,18Si,8S。 H,C,N,R,P=。 奇 奇或偶 偶 奇 I=1 B(1=,0=,H1=10. N(I-1),gV(I=6)

以上所列原子核,多可供核磁共振研究,其中以H最 容易测出,因此,目前农药分析中最常用的是H一NMR 的测定也是本章的重点。其次,用的较多的是3C、31P和 19F。虽然13C的天然丰度很小,只有1.069%(1H为 99.9844%,19F为100%,31P为100%)。且其信号灵敏度 只有质子的1/63,较难测定。但近年来,由于仪器和操 作技术的改进,测定3CNMR谱在结构测定中已占十分重 要的地位。 在磁场中,各种核所产生的磁矩有一定的取向,由磁 量子数()决定,而磁量子数m由核的自旋量子数决定, 即: m=1,0-1),(0-2),.,-1由此,共有(21+1)个m 值。H,13C等核,其|=1/2,则只可能有两种取向,即 m=+1/2, 表示核磁矩顺着H0方向(个) m=-1/2, 表示核磁矩逆着H0方向()
以上所列原子核,多可供核磁共振研究,其中以1H最 容易测出,因此,目前农药分析中最常用的是1H—NMR 的测定也是本章的重点。其次,用的较多的是13C、 31P和 19F。虽然13C的天然丰度很小,只有1.069%( 1H为 99.9844%,19F为100%,31P为100%)。且其信号灵敏度 只有质子的1/63,较难测定。但近年来,由于仪器和操 作技术的改进,测定13C NMR谱在结构测定中已占十分重 要的地位。 在磁场中,各种核所产生的磁矩有一定的取向,由磁 量子数(m)决定,而磁量子数m由核的自旋量子数决定, 即: m=I,(I-1),(I-2),.,-I由此,共有(2I+1)个m 值。1H, 13C等核,其I=1/2,则只可能有两种取向,即 m=+1/2, 表示核磁矩顺着H0方向(↑) m=-1/2, 表示核磁矩逆着H0方向(↓)


质子磁矩的两种取向相当于两个能态。磁矩 方向与磁场相同(顺H方向)的,质子能态低,不 相同(逆H方向)的,质子能态高。 若以射频场照射磁场中的质子,当射频场的 能态与两个能态的能量差相等时,处于低能态的 质子就可吸收射频场的能量跃迁到高能态。这就 是核磁共振,上述两个能态间的能量差可以下式 表示: △E=hw 式中:普朗克常数h=(6.626176±0.000036)×10-34Js V一共振频率
质子磁矩的两种取向相当于两个能态。磁矩 方向与磁场相同(顺H0方向)的,质子能态低,不 相同(逆H0方向)的,质子能态高。 若以射频场照射磁场中的质子,当射频场的 能态与两个能态的能量差相等时,处于低能态的 质子就可吸收射频场的能量跃迁到高能态。这就 是核磁共振,上述两个能态间的能量差可以下式 表示: 式中:普朗克常数h=(6.626176±0.000036)×10-34 J·s v—共振频率。 E hv =