
第4章平面连杆机构 学习目的:本章主要介绍平面四杆机构的类型、特性、运动分析、力分析及运动设计等, 同时简要计论机构的效率和自锁问颗。 知识要点:了解图解法进行平面机构的运动分析:了解机械效率及自锁:掌握四杆机构的 基本型式及特点:熟悉平面四杆机构的演化方法:掌握平面四杆机构的基本 特性:掌握图解法设计平面四杆机构。 4.1概述 平面连杆机构是由一些刚性构件用低副联接组成的机构,又称为平面四杆机构 如果所有低副均为转动副,这种四杆机构就称为铰链四杆机构。 >平面连杆机构的优点: 1、低副联接,为面接触,所以承受压强小、便于润滑、磨损较轻,可承受较大 载荷。 2、结构简单,加工方便,构件之间的接触是有构件本身的几何约束来保持的, 所以构件工作可靠。 3、可使从动件实现多种形式的运动,满足多种运动规律的要求。 4、利用平面连杆机构中的连杆可满足多种运动轨迹的要求。 平面连杆机构的缺点: 1、根据从动件所需要的运动规律或轨迹来设计连杆机构比较复杂,精度不高。 2、运动时产生的惯性难以平衡,不适用于高速场合。 4.4四杆机构的基本形式及演化 4.4.1四杆机构的基本型式 全部用转动副组成的平面四杆机构称铰链四杆机构。它是平面四杆机构的基本型式, 其他型式的四杆机构都可看成是在它的基础上通过演化而成的。 平面四杆机构名称解释: 连杆 机架.周定件AD: 连杆-不与机架直接联接BC: 连架杆-与机架连接的杆AB、CD: 曲柄:能作整圈回转的连架杆AB: 摇杆:只能在小于360°内摆动的连架杆CD。 1.曲柄摇杆机构 两连架杆中一个为曲柄(AB),另一个为摇杆(CD)的四杆机构,称为曲柄摇杆机构。(如 上图)。 曲柄为主动件时,转动一摆动。如:搅拌机、雷达天线、送料机构
第 4 章 平面连杆机构 学习目的:本章主要介绍平面四杆机构的类型、特性、运动分析、力分析及运动设计等, 同时简要讨论机构的效率和自锁问题。 知识要点:了解图解法进行平面机构的运动分析;了解机械效率及自锁;掌握四杆机构的 基本型式及特点;熟悉平面四杆机构的演化方法;掌握平面四杆机构的基本 特性;掌握图解法设计平面四杆机构。 4.1 概述 平面连杆机构是由一些刚性构件用低副联接组成的机构,又称为平面四杆机构。 如果所有低副均为转动副,这种四杆机构就称为铰链四杆机构。 ➢ 平面连杆机构的优点: 1、低副联接,为面接触,所以承受压强小、便于润滑、磨损较轻,可承受较大 载荷。 2、结构简单,加工方便,构件之间的接触是有构件本身的几何约束来保持的, 所以构件工作可靠。 3、可使从动件实现多种形式的运动,满足多种运动规律的要求。 4、利用平面连杆机构中的连杆可满足多种运动轨迹的要求。 ➢ 平面连杆机构的缺点: 1、根据从动件所需要的运动规律或轨迹来设计连杆机构比较复杂,精度不高。 2、运动时产生的惯性难以平衡,不适用于高速场合。 4.4 四杆机构的基本形式及演化 4.4.1 四杆机构的基本型式 全部用转动副组成的平面四杆机构称铰链四杆机构。它是平面四杆机构的基本型式, 其他型式的四杆机构都可看成是在它的基础上通过演化而成的。 平面四杆机构名称解释: 机架-固定件 AD; 连杆-不与机架直接联接 BC; 连架杆-与机架连接的杆 AB、CD; 曲柄:能作整圈回转的连架杆 AB; 摇杆:只能在小于 3600 内摆动的连架杆 CD。 1. 曲柄摇杆机构 两连架杆中一个为曲柄(AB),另一个为摇杆(CD)的四杆机构,称为曲柄摇杆机构。(如 上图)。 曲柄为主动件时,转动→ 摆动。 如:搅拌机、雷达天线、送料机构

摇杆为原动件时,摆动一转动。如:缝纫机踏板机构、自行车、走步机 2.双曲柄机构 两连架杆均为曲柄的四杆机构称为双曲柄机构。 一般情况:主动曲柄等速转动→从动曲柄变速转动。 如:惯性筛、插床机构 特侧:、主动曲柄等速转动一从动曲柄也同速同向转动。 如:机车车轮一平行双曲 柄机构。 3.双摇杆机构 两连架杆均为摇杆的四杆机构称为双摇杆机构。 主动摇杆摆动→从动摇杆摆动(摆角不等)。如:飞机起落架机构、鹤式起 重机 特例:等腰梯形机构(两摇杆长度相等)。 如:车辆前轮的转向机构 4.4.2平面四杆机构的演化 现实中四杆机构有许多种形式,各种形式之间均有一定的内在联系,而且都可看作是 从基本的铰链四杆机构演化而来 演化的途径: 转动副变为移动副 >变更机架、杆长: >扩大转动副。 演化的目的: 改变从动件运动方式或运动规律,改善构件受力。 1.转动副变成移动副 A.曲柄摇杆机构一若D处的转动副变成移动副(D的中心移到无穷远处)→转化成 曲柄滑块机构。 注:曲柄滑块机构有两种型式:对心式、偏置式 B.曲柄滑块机构→若C处转动副演化为移动副滑道m半径增至无穷大)一变成双 滑块机构(杆2演化为滑块2)。 注:双滑块机构又称正弦机构,缝纫机针的运动就是它的应用实例。 2.扩大转动副 曲柄滑块机构→B处转动副扩大,包括了A转动副一转化成偏心轮机构。 经过这样的转化提高了偏心轴的强度和刚度,结构简化。常应用于传力较大的碎矿机 和冲床等机械中。 3.取不同的构件为机架 A.曲柄摇杆机构(图423)若取不同的构件为机架,可得到不同的机构 如以曲柄杆1为机架,可得到双曲柄机构(图423b): 如以曲柄的对边摇杆3为机架,可得到双摇杆机构(图4.23d): 如以连杆4为机架,可得到曲柄摇杆机构(图4.23c)。 B.同样,对于曲柄滑块机构(下图),选取不同构件为机架也可以得到不同型式的 机构
摇杆为原动件时,摆动→ 转动。 如:缝纫机踏板机构、自行车、走步机 2. 双曲柄机构 两连架杆均为曲柄的四杆机构称为双曲柄机构。 一般情况: 主动曲柄等速转动→ 从动曲柄变速转动。 如:惯性筛、插床机构 特例:主动曲柄等速转动→ 从动曲柄也同速同向转动。 如:机车车轮—平行双曲 柄机构。 3. 双摇杆机构 两连架杆均为摇杆的四杆机构称为双摇杆机构。 主动摇杆摆动→ 从动摇杆摆动(摆角不等)。 如:飞机起落架机构、鹤式起 重机 特例:等腰梯形机构(两摇杆长度相等)。 如:车辆前轮的转向机构 4.4.2 平面四杆机构的演化 现实中四杆机构有许多种形式,各种形式之间均有一定的内在联系,而且都可看作是 从基本的铰链四杆机构演化而来。 演化的途径: ➢ 转动副变为移动副; ➢ 变更机架、杆长; ➢ 扩大转动副。 演化的目的: 改变从动件运动方式或运动规律,改善构件受力。 1. 转动副变成移动副 A.曲柄摇杆机构→ 若 D 处的转动副变成移动副(D 的中心移到无穷远处) → 转化成 曲柄滑块机构。 注:曲柄滑块机构有两种型式:对心式、偏置式 B.曲柄滑块机构→ 若 C 处转动副演化为移动副(滑道 nn 半径增至无穷大) → 变成双 滑块机构(杆 2 演化为滑块 2)。 注:双滑块机构又称正弦机构,缝纫机针的运动就是它的应用实例。 2. 扩大转动副 曲柄滑块机构→ B 处转动副扩大,包括了 A 转动副→ 转化成偏心轮机构。 经过这样的转化提高了偏心轴的强度和刚度,结构简化。常应用于传力较大的碎矿机 和冲床等机械中。 3. 取不同的构件为机架 A.曲柄摇杆机构(图 423a)若取不同的构件为机架,可得到不同的机构。 如以曲柄杆 1 为机架,可得到双曲柄机构(图 4.23b); 如以曲柄的对边摇杆 3 为机架,可得到双摇杆机构(图 4.23d); 如以连杆 4 为机架,可得到曲柄摇杆机构(图 4.23c)。 B.同样,对于曲柄滑块机构(下图 a),选取不同构件为机架也可以得到不同型式的 机构
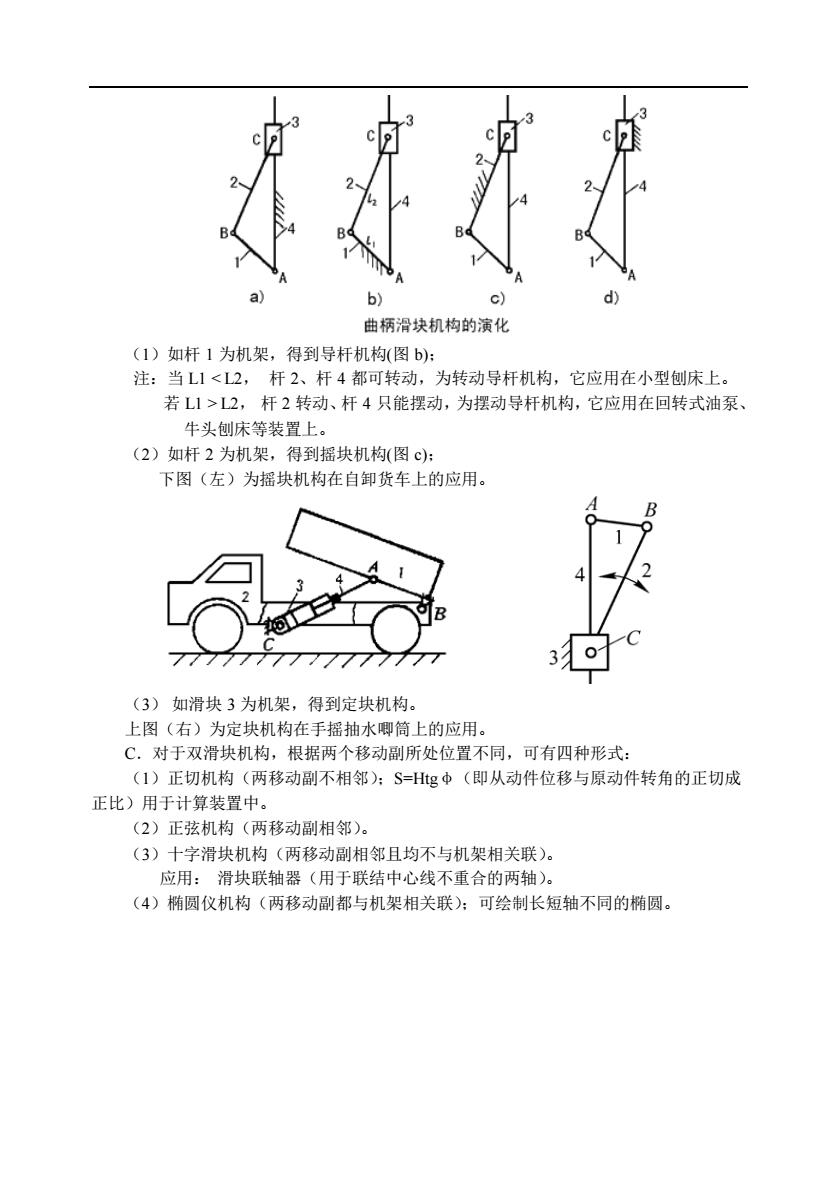
曲柄滑块机构的演化 (1)如杆1为机架,得到导杆机构(图b): 注:当L1L2,杆2转动、杆4只能摆动,为摆动导杆机构,它应用在回转式油泵、 牛头创床等装置上。 (2)如杆2为机架,得到摇块机构(图c): 下图(左)为摇块机构在自卸货车上的应用。 77777777777 3 (3)如滑块3为机架,得到定块机构。 上图(右)为定块机构在手摇抽水卿筒上的应用。 C.对于双滑块机构,根据两个移动副所处位置不同,可有四种形式: (1)正切机构(两移动副不相邻):S=Hg中(即从动件位移与原动件转角的正切成 正比)用于计算装置中。 (2)正弦机构(两移动副相邻)。 (3)十字滑块机构(两移动副相邻且均不与机架相关联)。 应用:滑块联轴器(用于联结中心线不重合的两轴) (4)椭圆仪机构(两移动副都与机架相关联):可绘制长短轴不同的椭圆
(1)如杆 1 为机架,得到导杆机构(图 b); 注:当 L1 L2, 杆 2 转动、杆 4 只能摆动,为摆动导杆机构,它应用在回转式油泵、 牛头刨床等装置上。 (2)如杆 2 为机架,得到摇块机构(图 c); 下图(左)为摇块机构在自卸货车上的应用。 (3) 如滑块 3 为机架,得到定块机构。 上图(右)为定块机构在手摇抽水唧筒上的应用。 C.对于双滑块机构,根据两个移动副所处位置不同,可有四种形式: (1)正切机构(两移动副不相邻);S=Htgφ(即从动件位移与原动件转角的正切成 正比)用于计算装置中。 (2)正弦机构(两移动副相邻)。 (3)十字滑块机构(两移动副相邻且均不与机架相关联)。 应用: 滑块联轴器(用于联结中心线不重合的两轴)。 (4)椭圆仪机构(两移动副都与机架相关联);可绘制长短轴不同的椭圆

d 正切机构 4.5平面四杆机构的基本特性 4.5.1铰链四杆机构有曲柄的条件 设:一曲柄摇杆机构ABCD,各杆长为a、b、c、d,AB为曲柄,a<d,曲柄整周回 转必能通过与机架AD平行的两位置AB'和AB"。 当曲柄处于AB时,形成△B'CD,则有: a+d <b+c 当曲柄处于AB"时,形成△B"C"D,则有: bs(d-atc即a+bsd+c c<d.a+b即a+c<d+b 将上述3式两两相加,可得: a≤d,a<b,a≤c 通过上面的分析,可以说明两个问愿: (1)在曲柄摇杆机构中,曲柄为最短杆: (2)最短杆与最长杆长度之和小于或等于其他两杆长度之和。 结谂:最短杆和最长杆长度之和小于或等于其余两杆长度之和是铰链四杆机构有曲 柄的必要条件。(不满足这一条件的,必为双摇杆机构。) 但满足这一条件的铰链四杆机构究竟有一个曲柄、两个曲柄还是没有曲柄,还需根据: 取何杆为机架来判断。 以最短杆为机架时得到双曲柄机构: 以最短杆的相邻杆为机架时得到曲柄摇杆机构: (以最短杆的对面杆为机架时得到双摇杆机构。 4.5.2压力角和传动角 1.压力角a 压力角:从动件所受的力F与受力点
4.5 平面四杆机构的基本特性 4.5.1 铰链四杆机构有曲柄的条件 设:一曲柄摇杆机构 ABCD,各杆长为 a、b、c、d,AB 为曲柄,a<d,曲柄整周回 转必能通过与机架 AD 平行的两位置 AB′和 AB″。 当曲柄处于 AB′时,形成△B′C′D,则有: a+d ≤b+c 当曲柄处于 AB″时,形成△B″C″D,则有: b≤(d-a)+c 即 a+b ≤d+c c≤(d-a)+b 即 a+c ≤d+b 将上述 3 式两两相加,可得: a≤d , a≤b , a≤c 通过上面的分析,可以说明两个问题: (1)在曲柄摇杆机构中,曲柄为最短杆; (2)最短杆与最长杆长度之和小于或等于其他两杆长度之和。 结论: 最短杆和最长杆长度之和小于或等于其余两杆长度之和是铰链四杆机构有曲 柄的必要条件。(不满足这一条件的,必为双摇杆机构。) 但满足这一条件的铰链四杆机构究竟有一个曲柄、两个曲柄还是没有曲柄,还需根据: 取何杆为机架来判断。 以最短杆为机架时得到双曲柄机构; 以最短杆的相邻杆为机架时得到曲柄摇杆机构; 以最短杆的对面杆为机架时得到双摇杆机构。 4.5.2 压力角和传动角 1.压力角α 压力角:从动件所受的力 F 与受力点

速度V.所夹的锐角a。 有效分力:F=Fcosa 有害分力:F.=Fsina α愈小,机构传动性能愈好。 通常amax≤500。 2.传动角Y 传动角:连杆与从动杆所夹的锐角Y。 传动角与压力角的关系为:Y=900-a Y越大,机构的传动性能越好,设计时一般应使Ymm≥4O0,对于高速大功率机械应 使Ymin≥500。 3.最小传动角的位置 曲柄摇杆机构在曲柄与机架共线的两位置出现最小传动角。 对曲柄滑块机构,当主动件为曲柄时,最小传动角出现在曲柄与机架垂直的位置。(此 位置传动性能最差) 对摆动导杆机构由于在任何位置时主动曲柄通过滑块传给从动杆的力的方向,与从动 杆上受力点的速度方向始终一致,所以传动角等于90度。(摆动导杆机构的传动性能最好) 4.5.3急回特性 是指机构从动件返回行程速度大于工作行程的特性 摆角中:摇杆在两极限位置间的夹角。 极位夹角:摇杆处于两极限位置时,曲柄所夹的锐角日。(也可 的锐角) 工作行程时:V1=CC2 返回行程时:V=C,Ct2 行程速比系数K:为了反映从动件“急回性 的程度,一般用行程速比系数K表示。 CC2/ -CC 1=2-180°+ >1 图0 49180°- /t
速度 Vc所夹的锐角 α。 有效分力:Ft=Fcosα 有害分力:Fn=Fsinα α愈小,机构传动性能愈好。 通常 αmax≤500。 2. 传动角γ 传动角:连杆与从动杆所夹的锐角 γ 。 传动角与压力角的关系为:γ = 900-α 。 γ 越大,机构的传动性能越好,设计时一般应使γmin≥400,对于高速大功率机械应 使γmin≥500。 3. 最小传动角的位置 曲柄摇杆机构在曲柄与机架共线的两位置出现最小传动角。 对曲柄滑块机构,当主动件为曲柄时,最小传动角出现在曲柄与机架垂直的位置。(此 位置传动性能最差) 对摆动导杆机构由于在任何位置时主动曲柄通过滑块传给从动杆的力的方向,与从动 杆上受力点的速度方向始终一致,所以传动角等于 90 度。(摆动导杆机构的传动性能最好) 4.5.3 急回特性 是指机构从动件返回行程速度大于工作行程的特性。 摆角ψ:摇杆在两极限位置间的夹角。 极位夹角θ:摇杆处于两极限位置时,曲柄所夹的锐角θ。(也可看成连杆之间所夹 的锐角) 工作行程时:V1=C1C2/t1 返回行程时:V2=C1C2/t2 行程速比系数 K: 为了反映从动件“急回性” 的程度,一般用行程速比系数 K 表示。 1 180 180 2 1 2 1 1 1 2 2 1 2 1 2 − + = = = = = t t t C C t C C V V K
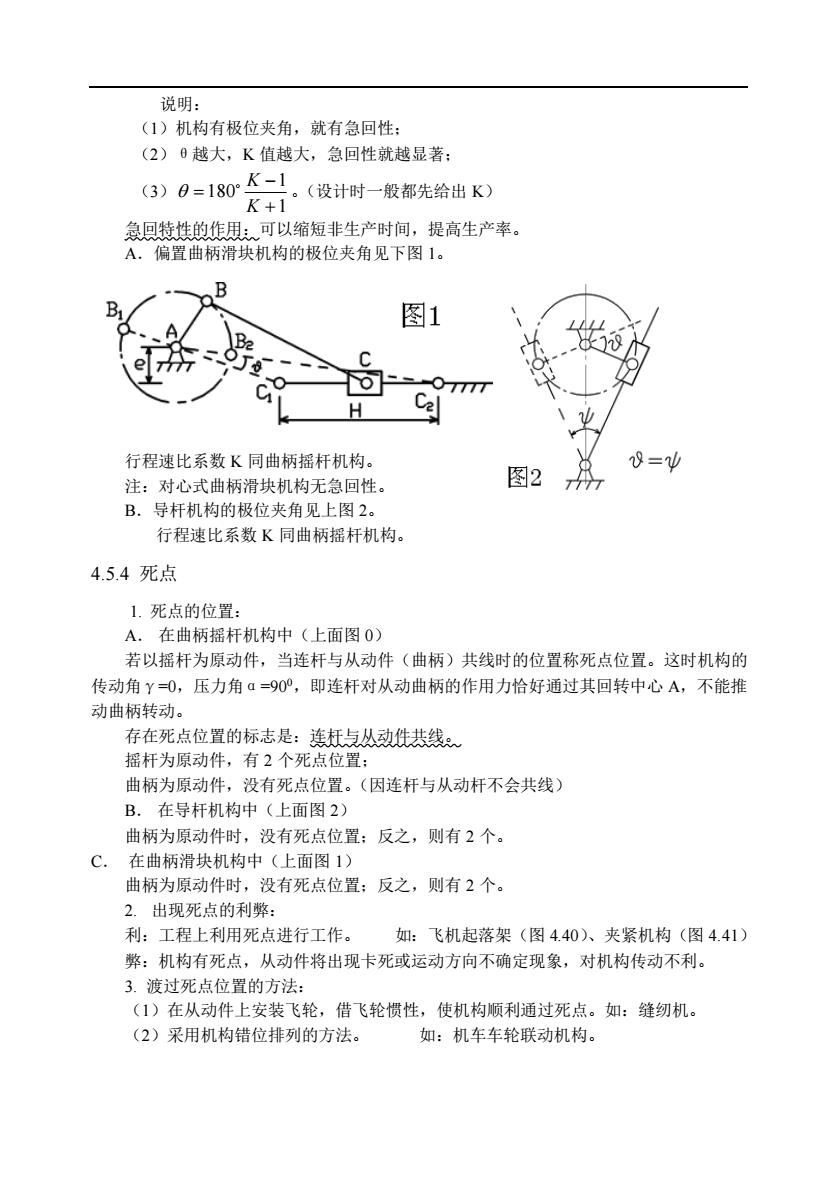
说明: (1)机构有极位夹角,就有急回性: (2)0越大,K值越大,急回性就越显著: (3)0=180K-。(设计时一般都先给出K) K+1 急回特性的作用:可以缩短非生产时间,提高生产率。 A。偏置曲柄滑块机构的极位夹角见下图1。 A 图1 H 行程速比系数K同曲柄摇杆机构。 8=Ψ 注:对心式曲柄滑块机构无急回性。 图2 B.导杆机构的极位夹角见上图2。 行程速比系数K同曲柄摇杆机构。 4.5.4死点 1.死点的位置: 在曲柄摇杆机构中(上面图0) 若以摇杆为原动件,当连杆与从动件(曲柄)共线时的位置称死点位置。这时机构的 传动角Y=0,压力角a=90,即连杆对从动曲柄的作用力恰好通过其回转中心A,不能推 动曲柄转动。 存在死点位置的标志是:连赶与从动件共线。 摇杆为原动件,有2个死点位置: 曲柄为原动件,没有死点位置。(因连杆与从动杆不会共线 B.在导杆机构中(上面图2) 曲柄为原动件时,没有死点位置:反之,则有2个。 C. 在曲柄滑块机构中(上面图1) 曲柄为原动件时,没有死点位置:反之,则有2个。 2.出现死点的利弊: 利:工程上利用死点进行工作。 如:飞机起落架(图4.40)、夹紧机构(图4.41 弊:机构有死点,从动件将出现卡死或运动方向不确定现象,对机构传动不利。 3.渡过死点位置的方法: (1)在从动件上安装飞轮,借飞轮惯性,使机构顺利通过死点。如:缝纫机。 (2)采用机构错位排列的方法。 如:机车车轮联动机构
说明: (1)机构有极位夹角,就有急回性; (2)θ越大,K 值越大,急回性就越显著; (3) 1 1 180 + − = K K 。(设计时一般都先给出 K) 急回特性的作用:可以缩短非生产时间,提高生产率。 A.偏置曲柄滑块机构的极位夹角见下图 1。 行程速比系数 K 同曲柄摇杆机构。 注:对心式曲柄滑块机构无急回性。 B.导杆机构的极位夹角见上图 2。 行程速比系数 K 同曲柄摇杆机构。 4.5.4 死点 1. 死点的位置: A. 在曲柄摇杆机构中(上面图 0) 若以摇杆为原动件,当连杆与从动件(曲柄)共线时的位置称死点位置。这时机构的 传动角γ=0,压力角α=900,即连杆对从动曲柄的作用力恰好通过其回转中心 A,不能推 动曲柄转动。 存在死点位置的标志是:连杆与从动件共线。 摇杆为原动件,有 2 个死点位置; 曲柄为原动件,没有死点位置。(因连杆与从动杆不会共线) B. 在导杆机构中(上面图 2) 曲柄为原动件时,没有死点位置;反之,则有 2 个。 C. 在曲柄滑块机构中(上面图 1) 曲柄为原动件时,没有死点位置;反之,则有 2 个。 2. 出现死点的利弊: 利:工程上利用死点进行工作。 如:飞机起落架(图 4.40)、夹紧机构(图 4.41) 弊:机构有死点,从动件将出现卡死或运动方向不确定现象,对机构传动不利。 3. 渡过死点位置的方法: (1)在从动件上安装飞轮,借飞轮惯性,使机构顺利通过死点。如:缝纫机。 (2)采用机构错位排列的方法。 如:机车车轮联动机构

4.6平面四杆机构的设计 一个设计过程:由己知条件一设计出各构件尺寸 √已知条件: 运动条件(如:从动件的运动规律) 几何条件(如:杆的尺寸范围) 动力条件(如:满足Ymin>400) 两类基本问题 √实现给定运动规律:(位置、速度、加速度、行程速比系数K) √实现给定运动轨迹。 三种设计方法: √图解法利用几何作图原理求解:图解法比较简明易懂,求解快,手工绘图精度 稍差:但计算机绘图已完全解决这一问题,其精度远远满足工程需要。 解析法:利用和构建设计参数间的函数关系求解:可以使设计呈参数化,精度高 但比较繁杂,如今利用计算机(CAD)也使得解析法变得轻松和容易。 √实验法:利用试凑法和连杆曲线图谱等方法求解:实验法直观、迅速,可近似达 到要求,常用作设计的预选。 4.6.1图解法设计平面四杆机构 图解法设计步骤: (1)将己知的几何条件能画出的尽可能画出: (2)将给定的运动条件转化为几何条件:(这一步往往要应用一些平面几何知识) (3)根据其他辅助条件求出所需机构。 注意:对动力学条件(如Ym),若给定的辅助条件中没有,或设计作图过程中也没 有涉及到,则求得的机构,还要校核Ym是否在允许值范围内。 1.按给定连杆位置设计四杆机构 已知:连杆BC长度及三个位置(B1C、B2C2、BC)。 要求:设计铰链四杆机构。(图4.42) 设计步骤: (I)连接B1B2、BB,作线BB2、B2B的垂直平分线b12、b23,交于A点: (2)连接C1C2、CC,作线CC2、CC3的垂直平分线c12、c23,交于D点: (3)连接AB1、CD,即得所求。 2.按给定两连架杆的对应位置设计四杆机构 解决此类问题常用刚化反转法。 所谓刚化反转法即将四杆机构在某一位置刚化后反 转一个角度。刚化反转的演示如下: 若己知机架AD、连架杆AB的长度及连架杆AB、CD的两组对应位置a1、中1和a2 中2,试设计该铰链四杆机构。(图4.43》 此问颗的关键是求较链C的位置 将AB2C2D刚化后绕D点反转(中~中2)角,CD与CD重合,AB2转到A'B2'的位 置。注意:经过转换,A、A'点相当于绕D点转动,B1、B2'点相当于绕C1点转动。这
4.6 平面四杆机构的设计 一个设计过程:由已知条件→设计出各构件尺寸 ✓ 已知条件: 运动条件(如:从动件的运动规律) 几何条件(如:杆的尺寸范围) 动力条件(如:满足γmin>400) 两类基本问题: ✓ 实现给定运动规律;(位置、速度、加速度、行程速比系数 K) ✓ 实现给定运动轨迹。 三种设计方法: ✓ 图解法;利用几何作图原理求解;图解法比较简明易懂,求解快,手工绘图精度 稍差;但计算机绘图已完全解决这一问题,其精度远远满足工程需要。 ✓ 解析法;利用和构建设计参数间的函数关系求解;可以使设计呈参数化,精度高, 但比较繁杂,如今利用计算机(CAD)也使得解析法变得轻松和容易。 ✓ 实验法:利用试凑法和连杆曲线图谱等方法求解;实验法直观、迅速,可近似达 到要求,常用作设计的预选。 4.6.1 图解法设计平面四杆机构 图解法设计步骤: (1)将已知的几何条件能画出的尽可能画出; (2)将给定的运动条件转化为几何条件;(这一步往往要应用一些平面几何知识) (3)根据其他辅助条件求出所需机构。 注意:对动力学条件(如γmin),若给定的辅助条件中没有,或设计作图过程中也没 有涉及到,则求得的机构,还要校核γmin 是否在允许值范围内。 1. 按给定连杆位置设计四杆机构 已知:连杆 BC 长度及三个位置(B1C1、B2C2、B3C3)。 要求:设计铰链四杆机构。(图 4.42) 设计步骤: (1) 连接 B1B2、B2B3,作线 B1B2、B2B3 的垂直平分线 b12、b23,交于 A 点; (2) 连接 C1C2、C2C3,作线 C1C2、C2C3 的垂直平分线 c12、c23,交于 D 点; (3) 连接 AB1、C1D,即得所求。 2. 按给定两连架杆的对应位置设计四杆机构 解决此类问题常用刚化反转法。 所谓刚化反转法即将四杆机构在某一位置刚化后反 转一个角度。刚化反转的演示如下: 若已知机架 AD、连架杆 AB 的长度及连架杆 AB、CD 的两组对应位置α1、φ1 和α2、 φ2,试设计该铰链四杆机构。(图 4.43) 此问题的关键是求铰链 C 的位置。 将 AB2C2D 刚化后绕 D 点反转(φ1-φ2)角,C2D 与 C1D 重合,AB2 转到 A′B2′的位 置。注意:经过转换,A、A′点相当于绕 D 点转动,B1、B2′点相当于绕 C1 点转动。这

样原问题可转化为按连杆的两位置设计四杆机构。 3.按给定行程速比系数K设计四杆机构 A.按给定行程速比系数K设计曲柄摇杆机构 设已知摇杆CD的长度c、摆角中和行程速比系数K,试设计该曲柄摇杆机构。 该设计的关键是确定固定铰链A的位置。设计步骤如下:(图4.45) (1)选取适当比例尺μL,按c和中作出摇杆的两个极限位置CD和CD: (2)按式0=180K=算出极位夹角: K+1 (3)连接C1C2,作∠CC20=∠C2C10=90°-0,以0为圆心、0C为半径作圆n, ∠C10C2=20: (4) 在圆n上,弧CC2所对圆周角上取A点,∠C1OC2=,则AC、AC,即为曲柄与 连杆共线的两个位置。设曲柄与连杆的长度分别为a和b, 则 u,·AC=b-a,μ:·AC=b+a 于是曲柄长度a=μ:(AC2-AC)/2 连杆长度b=μL(AC2+AC)/2 B.按给定行程速比系数K设计导杆机构 已知摆动导杆机构的机架长度d和行程速比系数K,试设计该机构。(图4.46) 解:取比例尺μ,作AD=d/μ1。由K算出8,由图可知,极位夹角等于导杆的摆 角中,因此作∠ADB1=∠ADB2=O/2,作AB,或AB垂直于B,D(或BD),则AB就是曲 柄,其长度a=uL·AB。 4.6.2解析法设计平面四杆机构 用解析法设计平面四杆机构时,首先要建立方程式,然后根据已知参数对方程式 求解。下面介绍解决按给定两连架杆对应位置设计四杆机构的问题。 已知:连架杆AB和CD的三对对应位置p1V1、922、p,要求确定各构件的长度 a、b、c、d。(图4.47) 分析:此机构各杆长度按同一比例增减时,各杆转角间的关系不变,故只需确定各杆 的相对长度,取a=l,则待求参数只有三个。 由于该机构四杆组成封闭多边形,因而有矢量方程式: a+b=d+c(二边矢量和等于第三边矢量) 为便于用解析法,可取直角坐标系XAY(以机架AD为X轴),取各杆在X、Y轴的 投影分别代入上式可得: cosp+bcos6=d ccosw sin+bsin=csinw 消去8,整理,并令:R=c、R=-(c/d)、R=(d+c2+1-b2V2d 得: cos中=R1cos+Rcog-中)+R3
样原问题可转化为按连杆的两位置设计四杆机构。 3. 按给定行程速比系数 K 设计四杆机构 A. 按给定行程速比系数 K 设计曲柄摇杆机构 设已知摇杆 CD 的长度 c、摆角 ψ 和行程速比系数 K,试设计该曲柄摇杆机构。 该设计的关键是确定固定铰链 A 的位置。设计步骤如下:(图 4.45) (1) 选取适当比例尺μL,按 c 和 ψ 作出摇杆的两个极限位置 C1D 和 C2D; (2) 按式 1 1 180 + − = K K 算出极位夹角θ; (3) 连接 C1C2,作∠C1C2O=∠C2C1O=90°-θ,以 O 为圆心、OC1 为半径作圆η, ∠C1 O C2=2θ; (4) 在圆η上,弧 C1C2 所对圆周角上取 A 点,∠C1 O C2=,则 AC1、AC2 即为曲柄与 连杆共线的两个位置。设曲柄与连杆的长度分别为 a 和 b, 则 μL·AC1=b-a , μL·AC2= b+a 于是 曲柄长度 a=μL(AC2 - AC1)/2 连杆长度 b=μL(AC2 + AC1)/2 B.按给定行程速比系数 K 设计导杆机构 已知摆动导杆机构的机架长度 d 和行程速比系数 K,试设计该机构。(图 4.46) 解:取比例尺μL,作 AD=d/μL。由 K 算出θ,由图可知,极位夹角θ等于导杆的摆 角 ψ,因此作∠ADB1=∠ADB2=θ/2,作 AB1 或 AB2 垂直于 B1D(或 B2D),则 AB 就是曲 柄,其长度 a=μL·AB1。 4.6.2 解析法设计平面四杆机构 用解析法设计平面四杆机构时,首先要建立方程式,然后根据已知参数对方程式 求解。下面介绍解决按给定两连架杆对应位置设计四杆机构的问题。 已知:连架杆 AB 和 CD 的三对对应位置 φ1ψ1、φ2ψ2、φ3ψ3,要求确定各构件的长度 a、b、c、d。 (图 4.47) 分析:此机构各杆长度按同一比例增减时,各杆转角间的关系不变,故只需确定各杆 的相对长度,取 a=1,则待求参数只有三个。 由于该机构四杆组成封闭多边形,因而有矢量方程式: a + b = d + c (二边矢量和等于第三边矢量) 为便于用解析法,可取直角坐标系 XAY(以机架 AD 为 X 轴),取各杆在 X、Y 轴的 投影分别代入上式可得: cosφ + bcosδ = d + ccosψ sinφ + bsinδ = csinψ 消去 δ,整理,并令:R1=c、R2=-(c/d)、R3=(d2+c2+1-b 2 )/2d 得: cosφ = R1cosψ + R2cos(ψ-φ) + R3

上式即为两连架杆转角之间的关系式,将已知的三对对应转角p1y 、33分别 代入,可得方程组。解方程组求出R、R2、R,再将他们代入相应式子,即可求得b、c d(注:它们是相对于a的相对长度)。 若根据具体情况选定曲柄长度a后,则b、c、d均可确定
上式即为两连架杆转角之间的关系式,将已知的三对对应转角 φ1ψ1、φ2ψ2、φ3ψ3 分别 代入,可得方程组。解方程组求出 R1、R2、R3,再将他们代入相应式子,即可求得 b、c、 d(注:它们是相对于 a 的相对长度)。 若根据具体情况选定曲柄长度 a 后,则 b、c、d 均可确定
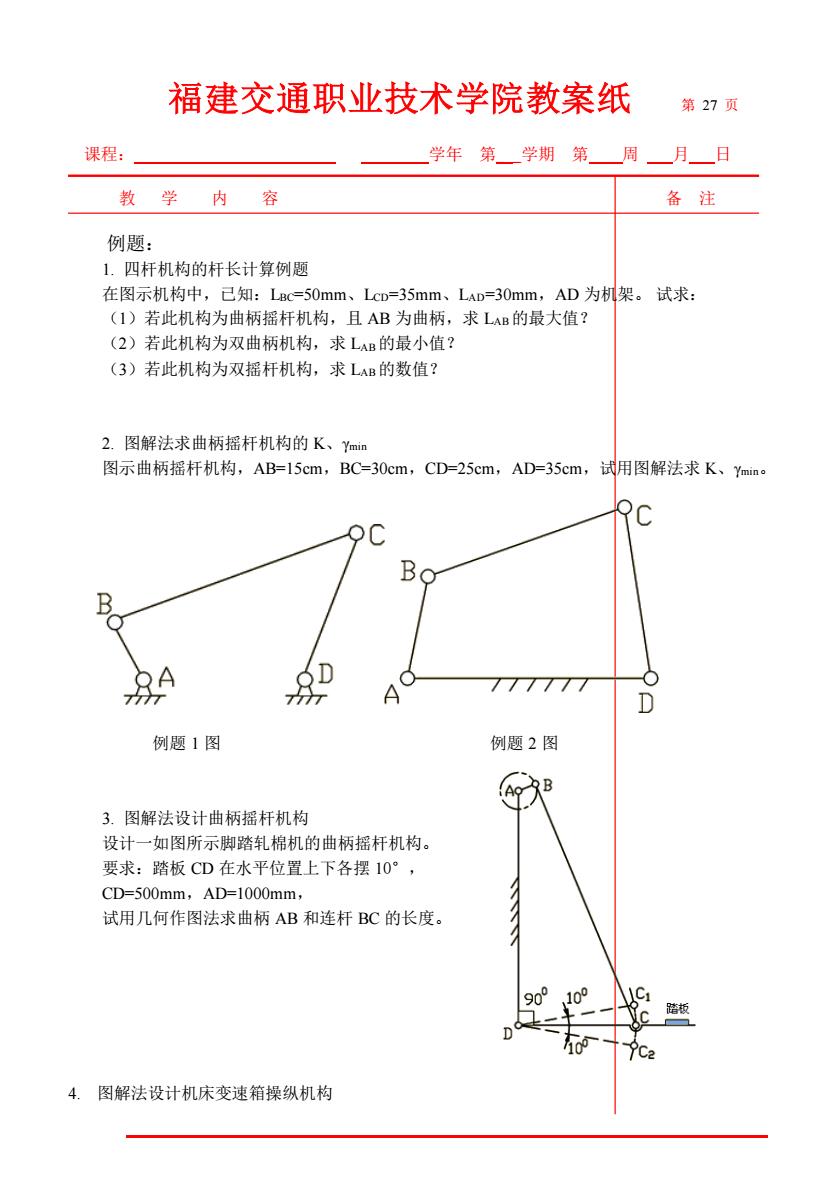
福建交通职业技术学院教案纸 第27项 课程: 学年第_学期第周一月一日 教学内容 备注 例题: 1.四杆机构的杆长计算例题 在图示机构中,已知:LBc=50mm、Lcp=35mm、LaD=30mm,AD为机架。试求: (1)若此机构为曲柄摇杆机构,且AB为曲柄,求LAB的最大值? (2)若此机构为双曲柄机构,求LB的最小值? (3)若此机构为双摇杆机构,求LAB的数值? 2.图解法求曲柄摇杆机构的K、Ymn 图示曲柄摇杆机构,AB=15cm,BC-30cm,CD=25cm,AD=35cm,试用图解法求K、Ymin。 B ● 0 例题1图 例题2图 3.图解法设计曲柄摇杆机构 设计一如图所示脚踏轧棉机的曲柄摇杆机构 要求:踏板CD在水平位置上下各摆10°, CD=500mm,AD=1000mm, 试用几何作图法求曲柄AB和连杆BC的长度。 4.图解法设计机床变速箱操纵机构
福建交通职业技术学院教案纸 第 27 页 课程: 学年 第_ _学期 第 周 月 日 教 学 内 容 备 注 例题: 1. 四杆机构的杆长计算例题 在图示机构中,已知:LBC=50mm、LCD=35mm、LAD=30mm,AD 为机架。 试求: (1)若此机构为曲柄摇杆机构,且 AB 为曲柄,求 LAB的最大值? (2)若此机构为双曲柄机构,求 LAB的最小值? (3)若此机构为双摇杆机构,求 LAB的数值? 2. 图解法求曲柄摇杆机构的 K、γmin 图示曲柄摇杆机构,AB=15cm,BC=30cm,CD=25cm,AD=35cm,试用图解法求 K、γmin。 例题 1 图 例题 2 图 3. 图解法设计曲柄摇杆机构 设计一如图所示脚踏轧棉机的曲柄摇杆机构。 要求:踏板 CD 在水平位置上下各摆 10°, CD=500mm,AD=1000mm, 试用几何作图法求曲柄 AB 和连杆 BC 的长度。 4. 图解法设计机床变速箱操纵机构