
结构动力特性 试验 宋世德 大连理工大学结构试验室 2010-11
结构动力特性 试验 宋世德 大连理工大学结构试验室 2010-11

内容 ◆一、 试验目的 ◆二、 试验原理 ◆三、 试验方法 ◆ 四、 试验过程 ◆五、数据处理 OFS EFPI
内容 ◆ 一、试验目的 ◆ 二、试验原理 ◆ 三、试验方法 ◆ 四、试验过程 ◆ 五、数据处理 OFS LPFG FBG EFPI

建筑结构动力特性是反映结构本身所 固有的动力性能。主要包括结构的自振频 率、阻尼系数和振型等动力特性参数。这 些特性反映结构本身所固有的动力性能, 是由结构形式、质量分布、结构刚度、材 料性质,构造连接等因素决定,与外荷载 无关。 建筑结构动力特性试验对结构动力特 性参数的量测是结构动力试验的基本内容, 在研究建筑结构或其他工程结构的抗震、 抗风或抗御其它动荷载的性能和能力时, 都必须要进行结构动力特性试验,以了解 结禊的自振特性。 EFPI
建筑结构动力特性是反映结构本身所 固有的动力性能 。主要包括结构的自振频 率、阻尼系数和振型等动力特性参数。这 些特性反映结构本身所固有的动力性能, 是由结构形式 、质量分布 、结构刚度 、 材 料性质,构造连接等因素决定,与外荷载 无关 。 建筑结构动力特性试验对结构动力特 性参数的量测是结构动力试验的基本内容 , 在研究建筑结构或其他工程结构的抗震、 抗风或抗御其它动荷载的性能和能力时 , 都必须要进行结构动力特性试验,以了解 结构的自振特性 。 结构的自振特性 OFS 。 LPFG FBG EFPI

通过结构动力特性试验,可以获得结 构的自振频率,(1)在结构抗震设计中 用于评估地震对结构的影响;(2)可以 避免动荷载作用下产生的共振。 结构受到损伤开裂后,结构的刚度发 生变化,而刚度的减弱使结构自振周期变 长,阻尼变大。因此结构动力特性试验可 用于结构的安全检测和结构损伤诊断,通 过结构自身固有特性的变化来识别结构物 的损伤程度,为结构的可靠度诊断和剩余 寿命的估计提供依据,最常见的是在桥检 中的应用
通过结构动力特性试验 ,可以获得结 构的自振频率,(1)在结构抗震设计中 用于评估地震对结构的影响;( 2 )可以 避免动荷载作用下产生的共振。 结构受到损伤开裂后,结构的刚度发 生变化 ,而刚度的减弱使结构自振周期变 长,阻尼变大。因此结构动力特性试验可 用于结构的安全检测和结构损伤诊断 , 通 过结构自身固有特性的变化来识别结构物 的损伤程度 ,为结构的可靠度诊断和剩余 寿命的估计提供依据,最常见的是在桥检 中的应用 。 OFS LPFG FBG EFPI 中的应用

一、试验目的 1、掌握动力参数的测量原理 2、掌握振动传感器、仪器及使用方法 3、通过振动衰减波形求出系统的固有 频率和阻尼比 4、掌握数据处理方法。 OFS EFPI
一、试验 的目 1、掌握动力参数的测量原理 2、掌握振动传感器、仪器及使用方法 3、通过振动衰减波形求出系统的固有 频率和阻尼比 4、掌握数据处理方法。 OFS LPFG FBG EFPI

m 二、试验原理 X k Hc ●单自由度系统是最简单的振动模型。 ●如果给系统(质量)一初始扰动,系统作 自由衰减振动,系统的运动微分方程式为: 久= C为阻尼系数,k为等效弹黄的弹性系数。 ●令 m 27 5子4 ## EFPI
二 试验原理 m 、 x k c x 单自由度系统是最简单的振动模型。 如果给系统(质量m)一初始扰动,系统作 自由衰减振动,系统的运动微分方程式为: c为阻尼系数,k为等效弹簧的弹性系数。 令 OFS LPFG FBG EFPI
方程的通解为: 为计算方便引入阻尼比3(相对阻尼系数):© 对于土木工程中常见的小阻尼(书<1,即Q<山)鞋箭解 为 € 式中:A为振幅,o为相位, 由运动初始条件确定 o为有阻尼自由振动的圆频率
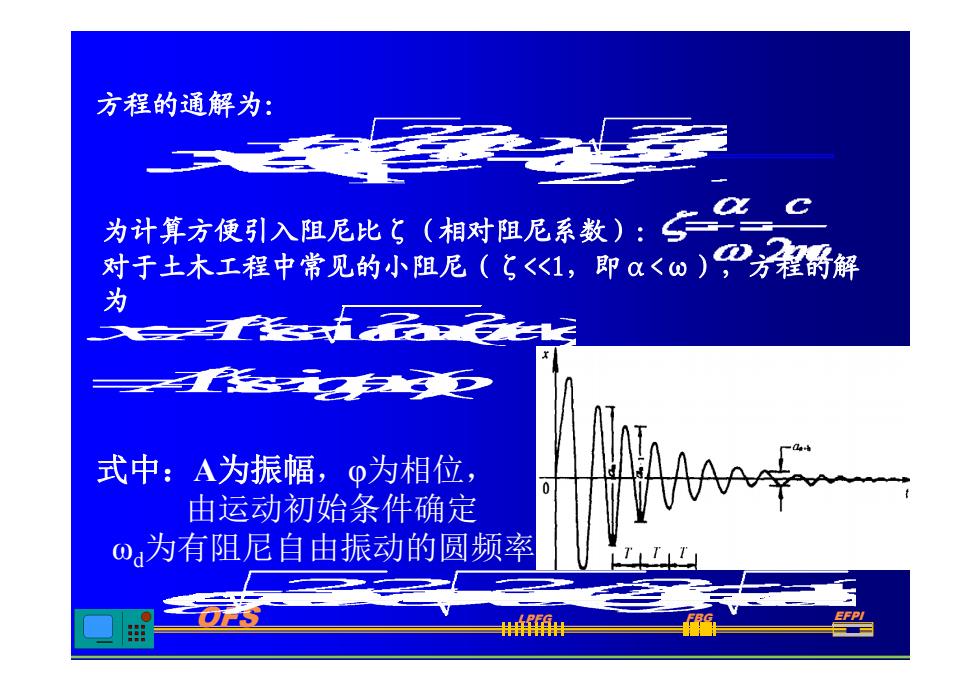
方程的通解为: 对于土木工程中常见的小阻尼(ζ<<1,即α<ω),方程的解 为计算方便引入阻尼比ζ(相对阻尼系数): 对于土木工程中常见的小阻尼(ζ<<1,即α<ω),方程的解 为 式中:A为振幅,φ为相位, 由运动初始条件确定 ωd为有阻尼自由振动的圆频率。 OFS LPFG FBG EFPI

有阻尼振动的特点: 1)有阻尼振动周期T大于无阻尼自由振周期T,即T,>T。 无阻尼条件时的系统固有频率: Z1号 由于阻尼的存在,使衰减振动的周期加大。通常阻 尼比化很小,阻尼对周期的影响不大。例如,当 G=0.05时,Td=1.00125T,周期Td仅增加了 0.127%。因此当阻尼比6《1时,可近似认为有阻尼 自由振动的周期与无阻尼自由振动的周期相等。 甜 OFS 踊# EFPI
有阻尼振动的特点: 1)有阻尼振动周期Td大于无阻尼自由振周期T,即Td>T。 无阻尼条件时的系统固有频率: 由于阻尼的存在,使衰减振动的周期加大。通常阻 尼比ζ很小,阻尼对周期的影响不大。例如,当 ζ=0 05 . 时,Td 1 =.00125T,周期Td 仅增加了 0.127%。因此当阻尼比ζ 《1时,可近似认为有阻尼 自由振动的周期与无阻尼自由振动的周期相等 OFS LPFG FBG EFPI

2)振幅按几何级数衰减。 振幅减缩率n则为 振幅对数减缩率为: a) ②2 若用相隔n个 周期的两个振 幅之比来计算: 测量振动波形的时刻ti和经过n个准周期后ti+nTd时的振幅, 可通过上式计算阻尼比能,从而确定阻尼系数c: EFPI
2) 振幅按几何级数衰减。 振幅减缩率 η则为 振幅对数减缩率为 : 若用相隔 n 个 周期的两个振 幅之比来计算: 测量振动波形的时刻ti和经过 n 个准周期后ti+nTd时的振幅, 可通过上式计算阻尼比 可通过上式计算阻尼比 ξ ,从而确定阻尼系数 从而确定阻尼系数 c: OFS LPFG FBG EFPI 近似为

总结:确定体系阻尼比的方法 工程实际中阻尼比常在0.02~0.2之间,远小于1,因此 EFPI
总结:确定体系阻尼比的方法 工程实际中阻尼比常在0.02~0.2之间,远小于1,因此 OFS LPFG FBG EFPI