
21s魘 第1章 食品系列数材 流体力学基础 本章的学习目的与要求 学习本章内容,学生能够完成食品工厂中输送水、气以及 稀溶液等牛顿流体的管道设计与计算工作,能够完成泵和风机 的选型配套工作。要求学生掌握实际流体与理想流体的区别; 掌握流体流动中各能量平衡方程的区别并能熟练运用这些方程 解决问题;掌握流体参数的测量原理和方法;掌握流体流动阻 力计算方法和系性能的计算方法;了解非牛顿流体种类和简单 计算

2食品工程原理 在食品加工中,我们会遇到很多种流体,如清洗和漂烫时所用的水;高温杀 菌时所用的蒸汽;干燥和速冻时所用的空气;牛奶、各种饮料、油、稀糖浆、蜂 蜜、苹果酱等食品材料。这些流体在加工过程中的流动特性差异较大,本章主要 讨论其速度、压力和流量、功率等问题,为管路设计和其他单元操作奠定基础。 基础知识与概念 1.1单位制 任何物理量的大小都是由数字和单位联合来表达的,在工程和科学中,有几 种单位制度。 (1)基本单位和导出单位一般选择几个独立的物理量(如质量、长度、时 间、温度等),根据使用方便的原则规定出它们的单位,这些选择的物理量称为 基本物理量,其单位称为基本单位。其他的物理量(如速度、加速度、密度等) 单位则根据其本身的物理意义,由有关基本单位组合而成。这种组合单位称为导 出单位。 (2)国际单位制(SI制)1960年10月第十一届国际计量大会通过了一种 新的单位制,称为国际单位制,其代号为SI,它是ks制的引申。SI制是一种 完整的单位制,它包括了所有领域中的计量单位,使科学技术、工农业生产、经 济贸易甚至日常生活中只使用一种单位制度,也就是SI制具有通用性的优点。 在SI制中,同一种物理量只有一个单位,如能量、热、功的单位都采用焦耳 (J),从而避免了不同单位制中热功之间换算因子的引入。这个优点称为“一贯 性”。 (3)《中华人民共和国法定计量单位》(简称法定单位制)以SI制为基础 我国于1984年颁布《中华人民共和国法定计量单位》及中华人民共和国国家标 准GB一3100~3102一93《量和单位》。我国的法定计量单位除SI制的基本单位 辅助单位和导出单位外,又规定了一些我国选定的非国际单位制单位。例如,时 间在我国还可以用分(min)、小时(h)、日(天)(d);质量可用吨(t);长度 可用海里(n mile)等单位计量。国际单位制和中华人民共和国法定计量单位制

第1章流体力学基础3 的内容。 1.2量纲分析 1.2.1量纲分析法的基本概念 量纲分析法是通过对描述某一过程或现象的物理量进行量纲分析,将物理量 组合为无量纲变量,然后借助试验数据,建立这些无量纲变量间的关系式。 量纲是表达某一物理量的符号,任何物理量都有自己量纲,在量纲分析中必 须把某些量纲定为基本量纲,而其他量纲则可由基本量纲来表示。在SI制中, 将长度L,时间0和质量m,温度T的量纲作为基本量纲,分别以[L]、 [T]、[M]和[日]表示。与食品工程流体流动有关的一些重要物理量均可以 M、L、T和日表示其纲量,如速度、压力、密度、粘度及比定压热容的纲量分 别为LT-1、ML-1T-2、ML-3、ML-1T-1及L2T-20-1。 量纲分析法的基础是量纲一致性的原则。也就是说,任何由物理定律导出的 方程,其各项的量纲是相同的。 1.2.2伯金汉元定理 许多问题,并没有恰当的控制微分方程可以使用。在此情况下,可以应用伯 金汉(Buckingham)提出的π定理。 设影响某一复杂现象的物理变量有n个,x1,x2,.,xn,则表达为一般 的函数关系时为: f(x1,x2,.,xn)=0 (1-1) 经过量纲分析和适当组合,上式可写成以无量纲变量表示的关系式。若以 N代表组合后的无量纲变量数目,则 F(π1,π2,.,πN) (1-2) π定理指出:由量纲分析所得的独立无量纲变量π的个数N等于影响该现 象的物理量数n减去这些物理量的基本量纲数m,即 N=n-m (1-3) 上述关系式可用数学方法予以证明。在此,基本量纲系指[L]、[T]

4食品工程原理 [M]和[8]。 下面以流体流经管路的摩擦阻力来说明π定理的应用。首先列出给定问题 的物理变量。根据对摩擦阻力的分析及相关的实验研究,可知由于流体的内摩擦 产生的压力降Ap:与下列诸因素有关:管径d,管长L,平均流速u,流体密度 ρ以及流体粘度4,写成函数关系式为: △pf=f1(d,L,u,p,u) (1-4) 将上式写成更普遍的函数形式: f(△p,d,L,u,p,u)=0 (1-5) 式中共有6个变量,即n=6;而基本量纲数为3个,即M、L、T,故 m=3。根据π定理,无量纲变量个数应为N=6-3=3,即经过无量纲分析后, 以无量纲变量表达的函数方程为: F(x1,π2,π3)=0 (1-6) 为量纲分析的方便,将式(1-4)写成如下幂函数的形式 △pf=adLupou (1-7) 式中a及指数a,b,.均为待定值。 将各物理量的量纲代入式(1-7)中,得 ML-1T-2=(L)a(L)b(LT-1)(ML-3)d(ML-1T-1)9 ML-IT-2 Md+eLa+b+e-3d-T-c-e 根据量纲一致性的原则,上式两侧各基本量纲的指数必须相等,于是可得下 列线性方程组: (d+e=1 a+b+c-3d-e=-1 (-c-e=-2 此方程组有3个方程,5个未知量,因此无法求解。为此,可将其中的两个 保留作为已知量处理,现保留b、,则由方程可以解出其他的3个未知量为: (a =-6-e c=2-e d=1-e

第1幸流体力学基础5 将所求得的a、c、d代人式(1-7)中,得 Api ad-b-'Lbub2-"pl-u 再将上式中指数相同的物理量和并,可得 兽=((e) (1-8) 或写成更一般的函数形式,为 r(台,2=0 (1-9) 再以无相变时的表面传热系数α为例,已知影响α的因素有:流体的粘度 H、密度p、热导率入、比定压热容cp、流速u,传热面几何尺寸l及BTg△t, 故函数关系应为: a=f(p,μ,入,cp,u,l,Brg△t) (1-10) 以幂函数表示,则有: a=kuarcppdu(BrgAt) (1-11) 在S制中各变量的量纲如下: a:T-38-1 P:ML-3 MT-IL-1 u:LT-1 A:MLT-38-1 L:L cp:L2T-20-1 BTg△t:LT-2 将各量纲式代入式(1-11): MT-38-1=(MT-1L-1)a(MLT-30-1)b(L2T-20-1)(ML-3)4 (LT-1)(LT-2)(L)8= Ma+b+dL-a+b+2c-3d+e+f+&T-a-36-2c-e-2fg-6-c 等式两边同量纲的指数相等,故有:

6食品工程原理 a+b+d=1 -a+b+2c-3d+e+f+g=0 -a-3b-2c-e-2f=-3 、-b-c=-1 联立解出下列4个未知数: a=c-e-2f b=1-c d=e+2f (g=e+3f-1 代回式(1-11)得 a=ku-21-crp+2u (BTgAt)+3-1 (1-12) 将相同次方的量合并在一起得: 受=(偿)(笑)广(2会学rrY (1-13) 从而得到特征数方程式: Nu kRe PrGrf (1-14) 这样就把一个含8个变量的复杂关系式变成只有4个量纲合为一的较简单的 关系式,从而大大减少了实验工作量。 各特征数的名称、符号和意义列于表1-1中。 表1-1特征数的符号和意义 特征数名称 符号 定义式 意义 努塞尔数 Nu 兴 表示表面传热系数 雷诺数 Re lup 确定流动状态 普兰特数 米 表示物性影响 格拉斯霍夫数 Gr Brg△l3e2 表示自然对流影响 e2
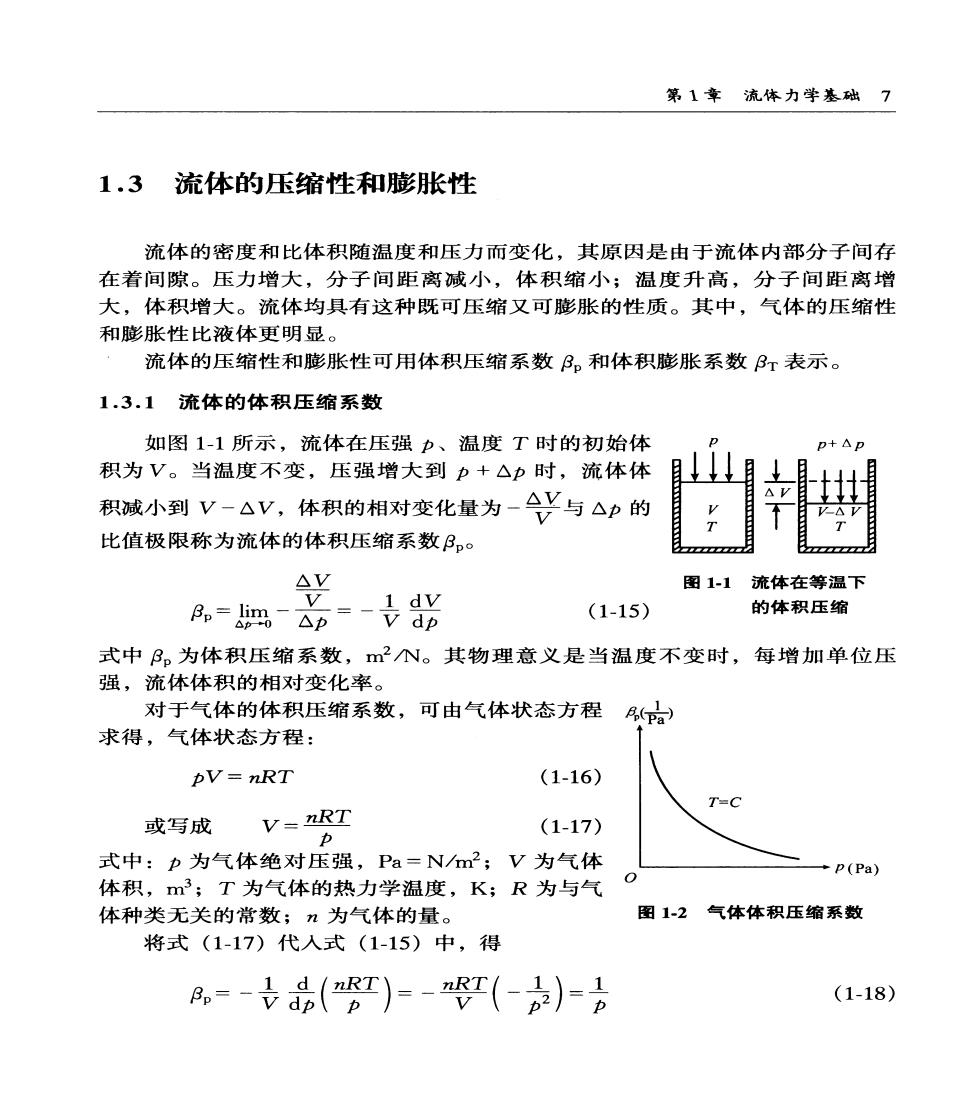
第1幸流体力学基础7 1.3流体的压缩性和膨胀性 流体的密度和比体积随温度和压力而变化,其原因是由于流体内部分子间存 在着间隙。压力增大,分子间距离减小,体积缩小;温度升高,分子间距离增 大,体积增大。流体均具有这种既可压缩又可膨胀的性质。其中,气体的压缩性 和膨胀性比液体更明显。 流体的压缩性和膨胀性可用体积压缩系数B。和体积膨胀系数B?表示。 1.3.1流体的体积压缩系数 如图1-1所示,流体在压强p、温度T时的初始体 积为V。当温度不变,压强增大到p+△p时,流体体 积减小到V-△V,体积的相对变化量为-兴与△p的 比值极限称为流体的体积压缩系数B,。 图1-1流体在等温下 =妈=卡 (1-15) 的体积压缩 式中B。为体积压缩系数,mN。其物理意义是当温度不变时,每增加单位压 强,流体体积的相对变化率。 对于气体的体积压缩系数,可由气体状态方程 B(Pa) 求得,气体状态方程: AV=nRT (1-16) T-C 或写成V=R工 (1-17) 力 式中:p为气体绝对压强,Pa=N/m;V为气体 -P(Pa) 体积,m3;T为气体的热力学温度,K;R为与气 0 体种类无关的常数;n为气体的量。 图1-2气体体积压缩系数 将式(1-17)代入式(1-15)中,得 ,=-t品(T)=-(-)=合 (1-18)

8食品工程原理 B。与p成反比,如图1-2所示。在气体状态方程式适用的范围内,压强越高, 气体的体积压缩系数越小,压缩越困推;反之,压强越低,气体越容易压缩。 对于液体的体积压缩系数,其值约为2×10(a),说明液体是不容易压缩的。 1.3.2流体的体积膨胀系数 如图1-3所示,流体在压强p、温度T时的初始体 积为V。当压强不变,温度增加到T+△T时,流体体 积膨胀到V+△V,体积相对变化量Y与△T比值的极 限称为流体的体积膨胀系数PT △V 图1-3流体在定压下 Br=AT=立d7 (1-19) 的体积膨胀 式中BT为体积膨胀系数,1K。其物理意义是,当压强不变时,每增加单位温 度所引起的流体体积的相对变化率。 对于气体体积膨胀系数,可由气体状态方程式代入式(1-19)求得 脚==T)贤= (1-20) Br与T成反比,如图1-4所示,在气体状态方程式的适用范围内,温度越 低,气体的体积膨胀系数越大。 液体的体积膨胀系数相对较小,如水在常温常 限) 压下的体积膨胀系数约为10000数量级。若液体中 含有气体,其体积膨胀系数将有所增大。 p=c 1.3.3不可压缩流体的概念 为了研究问题的方便,规定体积压缩系数和体 +K) 积膨胀系数完全为零的流体称为不可压缩流体。这 种流体受压体积不减小,受热体积不膨胀,因而, 图14气体体积膨胀系数 其密度和比体积均为常数。这样,在分析其能量平衡和运动规律时比较简单。 实际中,绝对不可压缩的流体是不存在的。但在通常情况下,液体以及低速 运动的气体其压缩性可以忽略,所得结果与实际情况非常接近

第1章流体力学基础9 2 牛顿流体及其粘度 流体在静止平衡时不能抵抗剪切变形,因而在 个y 平衡流体内部不存在切应力,可是当流体运动时情 →r 况就完全不同了。如图1-5所示,在相互平行且间 7777777+x 隙6很小的两平板之间充满液体,下板固定,上板 受F力作用并以匀速“沿x方向运动。由于流体 图15流体的粘性 与固体分子间的附着力,紧贴上板附近的一层流体黏附在上板并一起以速度 运动,紧贴下板附近的一层流体与下板一样固定不动。在流体内部由于液体分子 间的内聚力,上层流体必然带动下层流体流动,而下层流体也必然阻止上层流体 的流动,这样在流体内部层与层之间就产生了如1-5图所示的速度分布。层与层 之间也随之产生了内摩擦力或切应力x,流体的这种性质称为粘性。 2.1牛颅内摩擦定律 牛顿对图1-5所示的流动现象进行了实验研究,发现推动上板的外力F与 上板运动速度“及摩擦面积A成正比,与两板之间的距离8成反比,比例常数 “与两板之间的流体种类及其温度、压强有关,而与上板的正压力无关。由此得 出流体对上板的摩擦力为 F=H太A (1-21) 流体中的切应力为 x=界=u若 (1-22) 式中为沿与速度垂直方向每单位长度上的速度变化率,称为速度梯度。即流体 中的切应力与速度梯度成正比,如果两平板间的速度分布u=u(y)为直线规律, 则流体各横截面上各点的速度梯度是一个常数,沿流体截面的切应力分布如图1-5
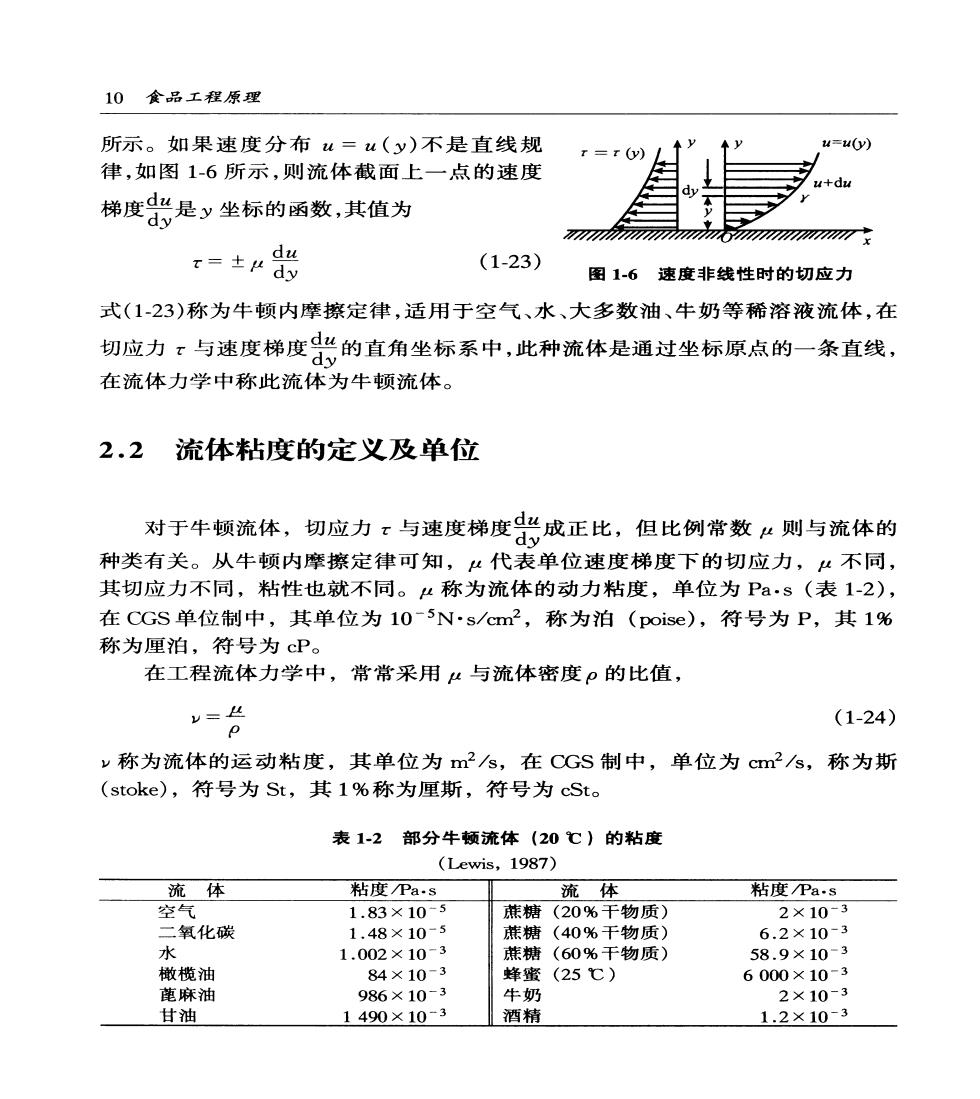
10食品工程原理 所示。如果速度分布u=u(y)不是直线规 r=r() -u(y) 律,如图1-6所示,则流体截面上一点的速度 -du 梯度北是y坐标的函数,其值为 7 72777777 r=士0 (1-23) 图16速度非线性时的切应力 式(1-23)称为牛顿内摩擦定律,适用于空气、水、大多数油、牛奶等稀溶液流体,在 切应力。与速度梯度的直角坐标系中,此种流体是通过坐标原点的一条直线, 在流体力学中称此流体为牛顿流体。 2.2流体粘度的定义及单位 对于牛顿流体,切应力。与速度梯度光成正比,但比例常数上则与流体的 种类有关。从牛顿内摩擦定律可知,以代表单位速度梯度下的切应力,“不同, 其切应力不同,粘性也就不同。4称为流体的动力粘度,单位为P·s(表1-2), 在CGS单位制中,其单位为10-5N·s/cm2,称为泊(poise),符号为P,其1% 称为厘泊,符号为cP。 在工程流体力学中,常常采用4与流体密度ρ的比值, =台 (1-24) y称为流体的运动粘度,其单位为m2/s,在CGS制中,单位为cm2/s,称为斯 (stoke),符号为St,其1%称为厘斯,符号为cSto 表1-2部分牛顿流体(20℃)的粘度 (Lewis,1987) 流体 粘度Pas 流体 粘度Pa·s 空气 1.83×10-5 蔗糖(20%干物质) 2×10-3 二氧化碳 1.48×10-5 蔗糖 (40%干物质) 6.2×10-3 水 1.002×10-3 蔗糖(60%干物质) 58.9×10-3 橄榄油 84×10-3 蜂蜜(25℃) 6000×10-3 蓖麻油 986×10-3 牛奶 2×10-3 甘油 1490×10-3 酒精 1.2×10-3