
21at 第7章 食品系列敏材 吸收与蒸馏 0000⊙0e00e0000⊙00◆0-◆0◆0.0⊙00000⊙ 本章的学习目的与要求 了解传质的基本概念、分子扩散与涡流扩散;了解扩散系 数的影响因素;掌握稳定分子扩散的基本计算与应用;了解吸 收与解吸的基本概念及吸收过程机理;掌握吸收与解吸的一般 计算方法;重点掌握等温条件下低浓度逆流吸收塔的计算与应 用;了解蒸(精)馏的基本概念;理解蒸(精)馏原理;了解 精馏装置的基本组成及各部分所起的作用;掌握逐板计算法及 图解法求取理论板数的方法;重点掌握两组分连续精馏塔的 计算

第7章吸收与蒸馏467 在食品工程原理中,各章节从内容上看是以单元操作划分,而从理论体系看 是以3种传递为基础的,吸收与蒸馏在食品工程中不仅是常见的单元操作,如二 氧化碳回收、含汽饮料生产、香精提取、酒精精馏等,更重要的是其理论隶属于 质量传递过程,阐述质量传递常以这两个单元操作为代表的。 如第2章所述,对非均相物系的分离,通常是利用多相物质在物理性质上的 差异来实现的。而对于均相混合物的分离,一般是采用引入另一相,利用各组分 物质在两相中性质(如溶解度、挥发度、表面张力等)的差异而由一相向另一相 转移的方法实现分离的。这种物质由一相向另一相转移的过程称为传质过程;除 了吸收、蒸馏外,萃取、吸附、膜分离、干燥等都是以传质为特征的单元操作。 本章首先介绍传质学的基础知识,通过3传的对比分析,突出质量传递与动 量传递、能量传递在研究方法上的可类比性;进而分别介绍双组分吸收和蒸馏 的原理、计算等,最终达到在工程实践中合理地设计及在实际操作中进行调节与 控制。 1 传质学基础 1.1混合物组成的表示方法 在讨论混合物分离操作中,离不开混合物的组成概念。在不同的场合下, 为了使用方便,混合物中组分的组成有若干表示方法,下面以双组分混合物为 例,给出两张表以阐述混合物的组成的各种表示法及其之间的换算关系(表7-1, 表7-2)。 表71混合物组成表示法 名称 符号 定义 单位 质量浓度 PA mA/V kg/m3 物质的量浓度 CA RA/V kmol/m3 质量分率 mA/(mA+mB) 无因次
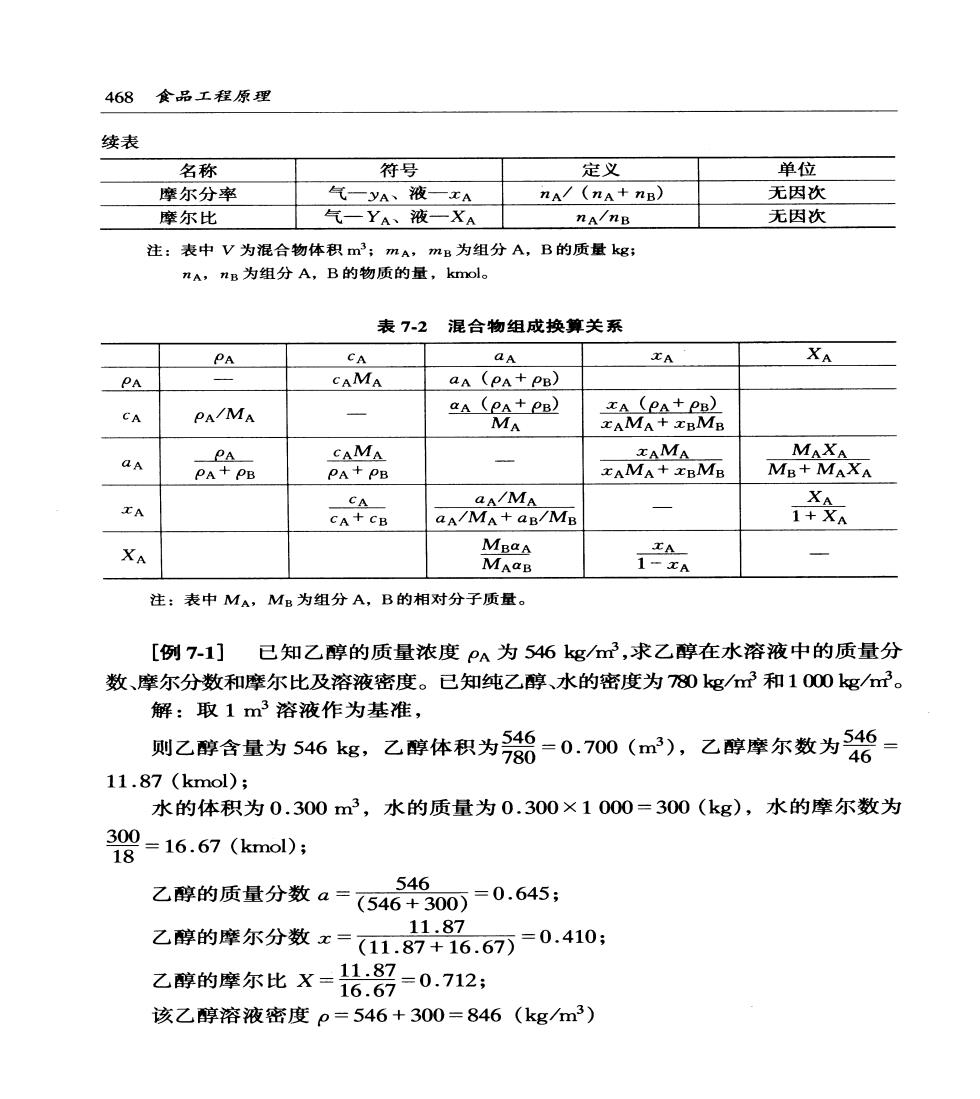
468食品工程原理 续表 名称 符号 定义 单位 摩尔分率 气yA、液—xA nA/(nA+nB) 无因次 摩尔比 气一YA、液一XA nA/nB 无因次 注:表中V为混合物体积m;mA,mB为组分A,B的质量kg: nA,nB为组分A,B的物质的量,kmol。 表7-2混合物组成换算关系 PA CA an XA PA CAMA aA (PA+PB) CA PA/MA 粉e 品。 aA pr阳 CAMA A MAXA PA+PB MB+MAXA IA CA CA+CB aNMA Ma 绕 XA MnaA MAQB 注:表中MA,MB为组分A,B的相对分子质量 [例7-1]已知乙醇的质量浓度P为546kg,求乙醇在水溶液中的质量分 数、摩尔分数和摩尔比及溶液密度。已知纯乙醇、水的密度为780kg/m3和1000g/m。 解:取1m3溶液作为基准, 则乙醇含量为546kg,乙醇体积为=0.700(m),乙醇摩尔数为 11.87(kmol); 水的体积为0.300m3,水的质量为0.300×1000=300(kg),水的摩尔数为 98=16.67(kmol0; 546 乙醇的质量分数a=(546+300)=0.645: 11.87 乙醇的摩尔分数x=(11.87+16.67列=0.410: 乙静的摩尔比X=沿部=0.712: 该乙醇溶液密度p=546+300=846(kgm3)

第7章吸收与蒸馏469 1.2扩散现象与分子扩散速率计算 扩散现象是一种物理现象,如在烧杯中盛满清水,滴人几滴红墨水,则杯中 水将逐渐变红色,最终色泽均匀,说明红墨水在水中发生了传质,这种由浓度 (或温度)不均引起,依靠微观分子运动产生传质的现象称分子扩散。上例中若 对杯中水加以搅拌,使水湍动,则混合均匀的时间将大为缩短,扩散效果加剧, 这种发生在湍流体中依靠质点宏观不规则运动的碰撞混合,而进行传质的现象称 为湍流扩散,或称涡流扩散。湍流时分子扩散依然存在,只是此时湍流扩散效果 更为显著。 1.2.1分子扩散与Fick定律 分子扩散的规律类似于热传导,即扩散速率与浓度梯度成正比。设均相二元 物系,由A,B两组分组成。由于浓度不等,而引起分子扩散,在单位时间内通 过单位面积传递的物质的量称为扩散通量。在恒定的温度和压强下,均相混合物 中,分子扩散服从费克定律(Fick'slaw),即对A组分: JA-DAnE (7-1) 式中:JA为A组分在之方向上的扩散通量,kmol/(m2·s);cA为A组分的量浓 度,kmol/m3;DAB为A组分在A,B的混合物中扩散时的扩散系数,m/s; “一”表示扩散沿着浓度降低方向进行。 对B组分: dcB JB=-Da dz (7-1a) 式中D为B组分在A,B两组分混合物中的扩散系数。当扩散为汽相或是两组 分性质相似的液相时,DAB=DA,故以后用D表示双组分物系的扩散系数。 对气体常用分压梯度表示,方向上等温扩散时,因人=学-会 D dpA JA=-RT dz (7-1b)

470食品工程原理 式中pA为A组分分压,Pa;T为气体的温度,K;R为气体常数,等于 8314J/(kmol-K);“-”表示扩散沿着浓度降低方向进行。 仿照分子扩散,将涡流扩散通量写为: A=-D. (7-2) 式中D。为涡流扩散系数,m/s,D。不是物性常数,它是由流体的动力状况 决定的,比D要复杂得多。因D很难求得,因此7-2式的应用受到很大限 制。 1.2.2分子扩散速率 以上所述分子扩散通量只是定义式,要在实际应用中计算其分子扩散速率还 必须根据具体情况进行分析,下面着重讨论经常碰到的两种汽相稳定分子扩散形 式,即等摩尔扩散和单向扩散。 (1)等摩尔扩散设想用一段粗细均匀的直管将两个很大的容器联通,如图 7-1(a)所示。两容器内有浓度不同的A,B两种气体的混合物,其中p1> 2,<,但两容器内混合气体的温度和总压强都相同,且两容器内均 装有搅拌器,使各自的浓度保持均匀。扩散时,因为两容器内总压强相同,所 以联通管内任一截面上单位时间、单位面积上向右传递的A分子的数量与向左 传递的B分子的数量必定相等,这便是等摩尔逆向扩散,即:pA+pB=p=常 dz dz JA=-JB 在任一固定的空间位置垂直于扩散方向的截面上,单位时间内通过单位截面 积的A的净物质量,称为A的传递速率,以NA表示。在等摩尔逆向扩散中, 物质A的传递速率应等于它的扩散通量,即: N=Jh=-D= DdpA (7-3) 在上述条件下,扩散为稳定过程,N应为常数。因而也是常数,故 pA一之呈线性关系,如图7-1(b)所示
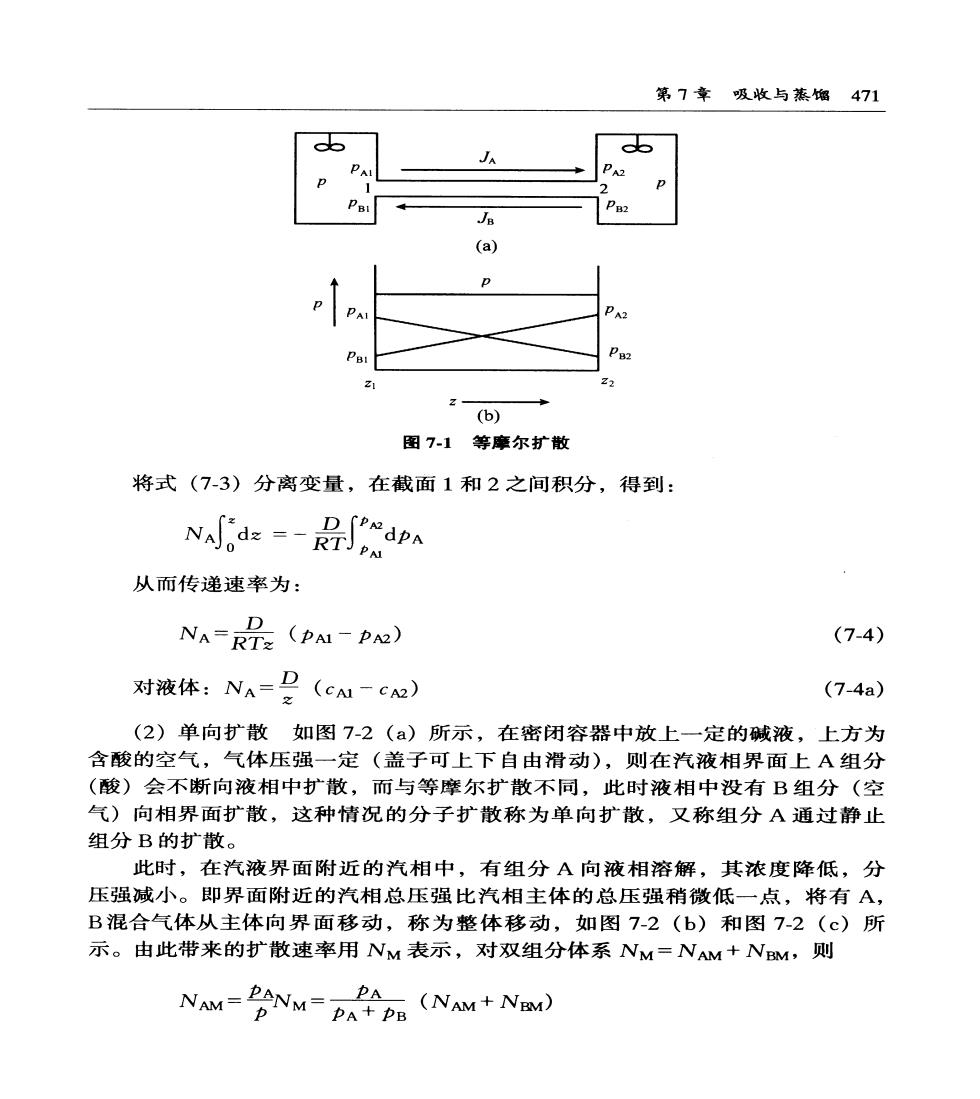
第7幸吸收与蒸馏471 a (a) D PA 2 (b) 图7-1等摩尔扩散 将式(7-3)分离变量,在截面1和2之间积分,得到: Nddp 从而传递速率为: D NA=RT2(PM1-PO) (7-4) 对液体:NA=P(cu-c) (7-4a) (2)单向扩散如图7-2(a)所示,在密闭容器中放上一定的碱液,上方为 含酸的空气,气体压强一定(盖子可上下自由滑动),则在汽液相界面上A组分 (酸)会不断向液相中扩散,而与等摩尔扩散不同,此时液相中没有B组分(空 气)向相界面扩散,这种情况的分子扩散称为单向扩散,又称组分A通过静止 组分B的扩散。 此时,在汽液界面附近的汽相中,有组分A向液相溶解,其浓度降低,分 压强减小。即界面附近的汽相总压强比汽相主体的总压强稍微低一点,将有A, B混合气体从主体向界面移动,称为整体移动,如图7-2(b)和图7-2(©)所 示。由此带来的扩散速率用NM表示,对双组分体系NM=NAM+NM,则 NAM-PANM-DAPA PE (NAM+N) PA
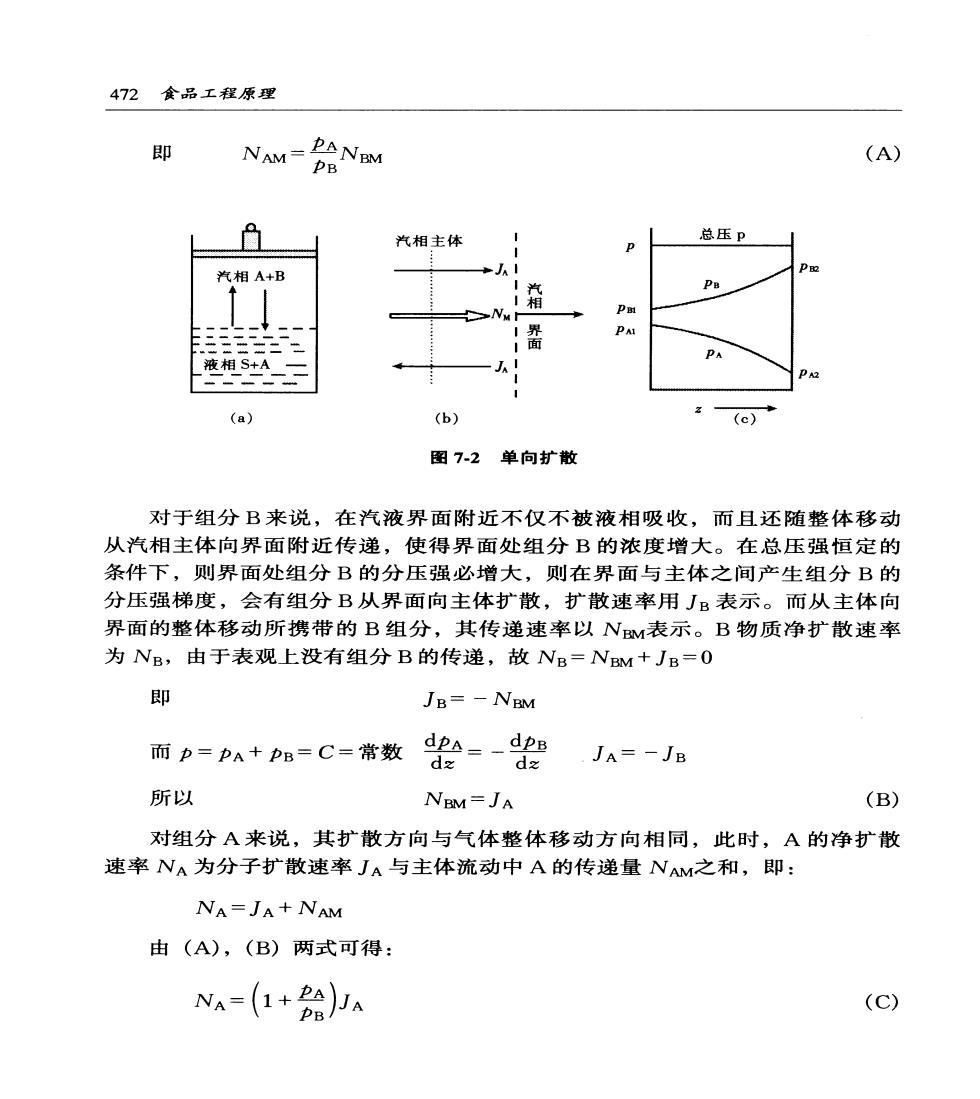
472食品工程原理 即 NM=PB会NaN (A) m 汽相主体 总压p 汽相A+B 汽相 P 相S+A (a) (b) (c) 图7-2单向扩散 对于组分B来说,在汽液界面附近不仅不被液相吸收,而且还随整体移动 从汽相主体向界面附近传递,使得界面处组分B的浓度增大。在总压强恒定的 条件下,则界面处组分B的分压强必增大,则在界面与主体之间产生组分B的 分压强梯度,会有组分B从界面向主体扩散,扩散速率用JB表示。而从主体向 界面的整体移动所携带的B组分,其传递速率以NM表示。B物质净扩散速率 为NB,由于表观上没有组分B的传递,故NB=NBM+JB=0 即 JB=-NBM 而p=pA+pB=C=常数2=-2JA=-JB 所以 NBM=JA (B) 对组分A来说,其扩散方向与气体整体移动方向相同,此时,A的净扩散 速率NA为分子扩散速率JA与主体流动中A的传递量NAM之和,即: NA=JA+NAM 由(A),(B)两式可得: NA-(1+B给Ja (C)

第7章吸收与蒸馏473 将式(7-1b)代入此式,求得: N是+)=是,。、器 (D) 将(D)式在之=O,pA=pA1与之=之,pA=pa之间进行积分。 Nd=-器,Pa 对于稳定吸收过程,NA为定值,操作条件一定,D,p,T均为常数,积 分得: N-器n名B别 因p=p1+pB1=P加十pm,将上式改写为: N-器如n D力(PM-P0) NA-RTzPBm (7-5) 式中pm=巴P型为组分B分压强的对数平均值。 In Pre 对液体则:NA=是品(cN-ca) (7-5a) 式中cm=S巴二C1为组分B浓度的对数平均值。 hS® CBI 此式即为所推导的单方向扩散时的传质速率方程式,式中p/pm总是大于 1,称为“漂流因子”或“移动因子”。与式(7-4)比较可知,单方向扩散的传 质速率NA比等摩尔逆向扩散时的传质速率JA大。这是因为在单方向扩散时除 了有分子扩散,还有混合物的整体移动所致。p/pm值越大,表明整体移动在传 质中所占分量就越大。当汽相中组分A的浓度很小时,各处pB都接近于p即 p/pm接近于1,此时整体移动便可忽略不计,可看做等摩尔逆向扩散。 1.2.3扩散系数 分子扩散系数是物质的物性常数之一,表示物质在介质中的扩散能力。扩散
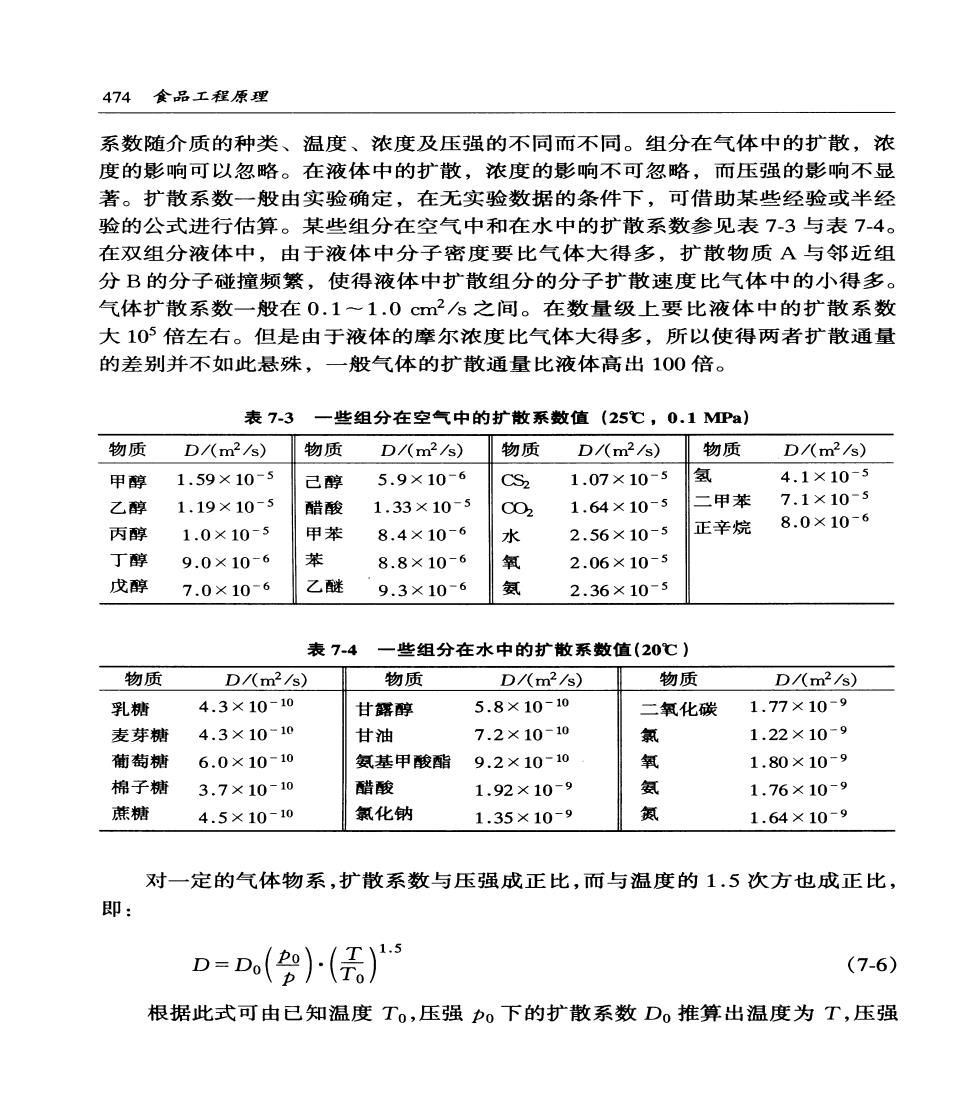
474食品工程原理 系数随介质的种类、温度、浓度及压强的不同而不同。组分在气体中的扩散,浓 度的影响可以忽略。在液体中的扩散,浓度的影响不可忽略,而压强的影响不显 著。扩散系数一般由实验确定,在无实验数据的条件下,可借助某些经验或半经 验的公式进行估算。某些组分在空气中和在水中的扩散系数参见表73与表74。 在双组分液体中,由于液体中分子密度要比气体大得多,扩散物质A与邻近组 分B的分子碰撞频繁,使得液体中扩散组分的分子扩散速度比气体中的小得多。 气体扩散系数一般在0.1~1.0cm2/s之间。在数量级上要比液体中的扩散系数 大105倍左右。但是由于液体的摩尔浓度比气体大得多,所以使得两者扩散通量 的差别并不如此悬殊,一般气体的扩散通量比液体高出100倍。 表7-3一些组分在空气中的扩散系数值(25℃,0.1MPa) 物质D/(m2/s)物质 D/(m2/s)物质 D/(m2/s)物质 D/(m2/s) 甲醇 1.59×10-5 己醇 5.9×10-6 CS2 1.07×10-5 氢 4.1×10-5 乙醇 1.19×10-5 醋酸 1.33×10-5 C02 1.64×10-5 二甲苯 7.1×10-5 8.0×10-6 丙醇 1.0×10-5 甲苯 8.4×10-6 水 2.56×10-5 正辛烷 丁醇 9.0×10-6 苯 8.8×10-6 氧 2.06×10-5 戊醇 7.0×10-6 乙醚 9.3×10-6 氨 2.36×10-5 表7-4一些组分在水中的扩散系数值(20℃) 物质 D/(m2/s) 物质 D/(m2/s) 物质 D/(m2/s) 乳糖 4.3×10-10 甘露醇 5.8×10-10 二氧化碳1.77×10-9 麦芽糖 4.3×10-10 甘油 7.2×10-10 1.22×10-9 葡萄糖 6.0×10-10 氨基甲酸酯9.2×10-10 氧 1.80×10-9 棉子糖 3.7×10-10 醋酸 1.92×10-9 晚 1.76×10-9 蔗糖 4.5×10-10 氯化钠 1.35×10-9 1.64×10-9 对一定的气体物系,扩散系数与压强成正比,而与温度的1.5次方也成正比, 即: D=()() (7-6) 根据此式可由已知温度T。,压强p0下的扩散系数Do推算出温度为T,压强

第7章吸收与燕馏475 为p时的扩散系数D。 液体的扩散系数与温度、粘度有关,一般可用下列经验公式表示,即: D=D君只 (7-7) 根据此式可由已知温度To,粘度o下的扩散系数Do,推算出温度为T,粘度 为μ时的扩散系数D。 [例7-2]有一个10cm高的烧杯内装满乙醇,问在101.3kPa(1atm)及25℃ 的室温下全部蒸干约需多少天?假设量筒口上方空气中乙醇蒸汽分压为0,若室 温升高至35℃,问全部蒸干约需多少天?已知25℃和35℃下乙醇的饱和蒸汽压分 别为8.0kPa和13.3kPa。 分析:此题属非稳定单向扩散问题.解决非稳定问题是在对扩散至某一时刻x (液面下降高度为之处)的瞬间,利用单向扩散传质速率方程,然后利用质量衡算 建立微分式,最后划定边界条件积分得所需时间x。 解:如图所示,设x时刻液面下降高度为z PBI =101.3 kPa,PAI=p-PBI=0 pm=101.3-8.0=93.3kPa,p2=8.0(kPa) p2一pB1 101.3-93.3 pm=n(p2/pm)=n(10i393.3)=97.2(kPa) 例7-2示意图 25℃乙醇在空气中的D=1.19×10-5m2/s,R=8.314 kJ/(kmol.K) 品是(pu-p加)=83品8文(g92)(8.0-0) NA -RTz PBm 1.19×10-5 4.00×10-8 Na=4.00×10-8/2 (A) dx时间内,液面高度降低dz,在此微元时间内,认为NA保持不变,则物料衡 算得 NA.A.dr=A.dz.p/M 将(A)式代入上式得: 4.00×10-8dx=(780/46)·z·dz (B)