习题一洛必达法则 1.lim 1-cosx= 401+c03x A.1 B.一1 CC.0 CD.不存在 -arctanx lim 2 x->4 2. C A.1 CB.一1 c.0 0D.c0 lim 3. C A.1 CB.一1 c.0 h(1+马 4. lim x→+arc cot x C A.1 CB.一1
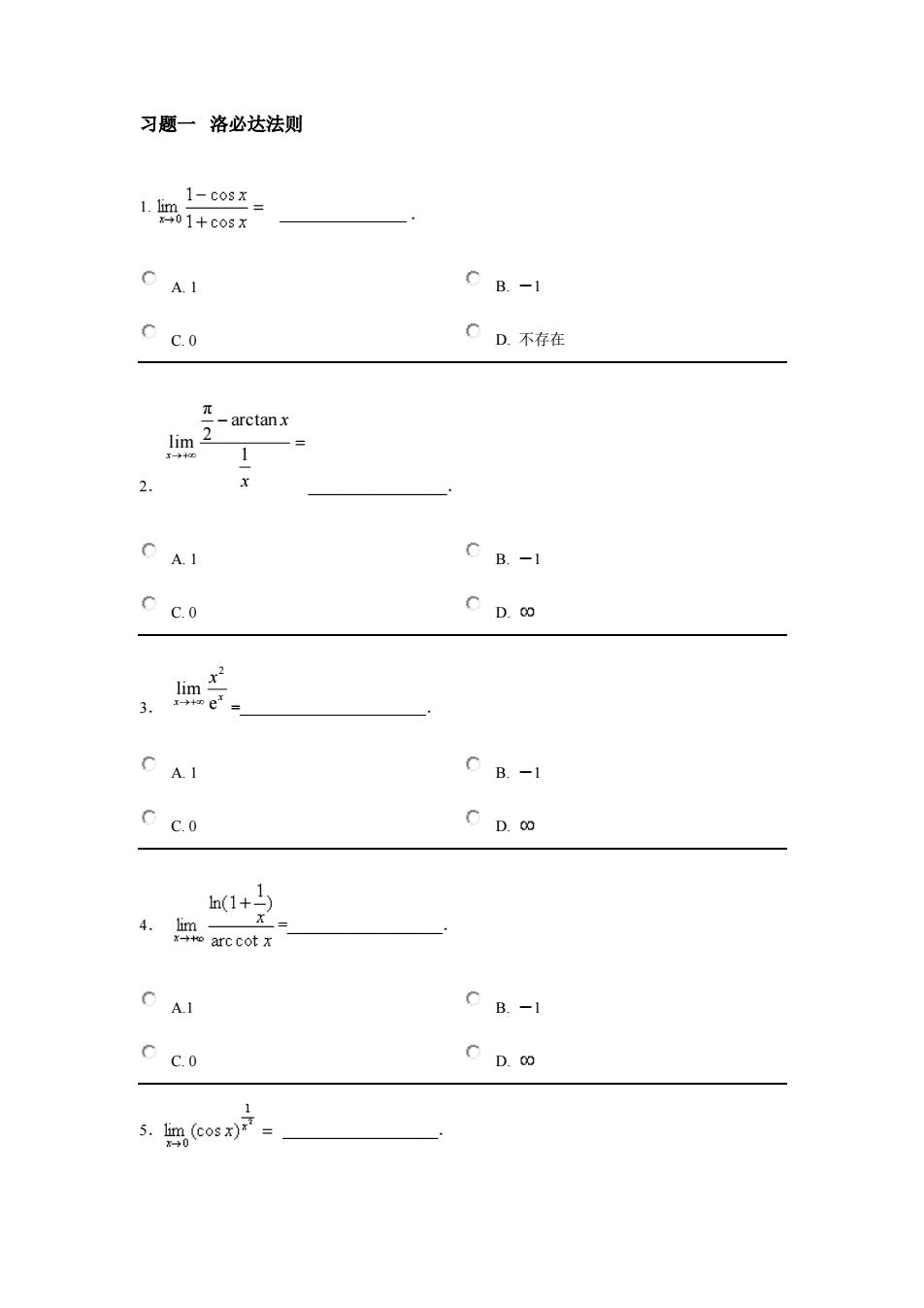
习题一 洛必达法则 1. . A. 1 B. -1 C. 0 D. 不存在 2. _________________. A. 1 B. -1 C. 0 D. 3. = . A. 1 B. -1 C. 0 D. 4. =___________________. A.1 B. -1 C. 0 D. 5. ___________________. x x x 1 arctan 2 π lim 2 lim e x x x
C A.e- c.0 C D.0o 1C.解原式不属于。型,不能用洛必达法则。正确的解法为: 0 1-cosx lim(1-cosx)1-1 lim -0 =0 01+CoSx lim(1+cosx)1+1 x→0 π 1 -arctanx 2.A.解.lim 2 =lim- +2 =1 1 r+ 1 x→*x2+1 3.c.解1imx.=lim2x 2x 2 =1im=0. ln1+-) 1+ 1+x2 4.A.解1im x=lim-x 1 lim r→+arcc0tXr→tm x-+40 1+x2 + 1+x2 xx=im lim 2x=1 +n1+2x 5.B.解lim(cosx)之=lime子asr= 1 =e ,其中 x→0 x-→0 因为lim Incosx lim -sinx x0 2xcOSx 所以1im(cosx产=e司 1 0
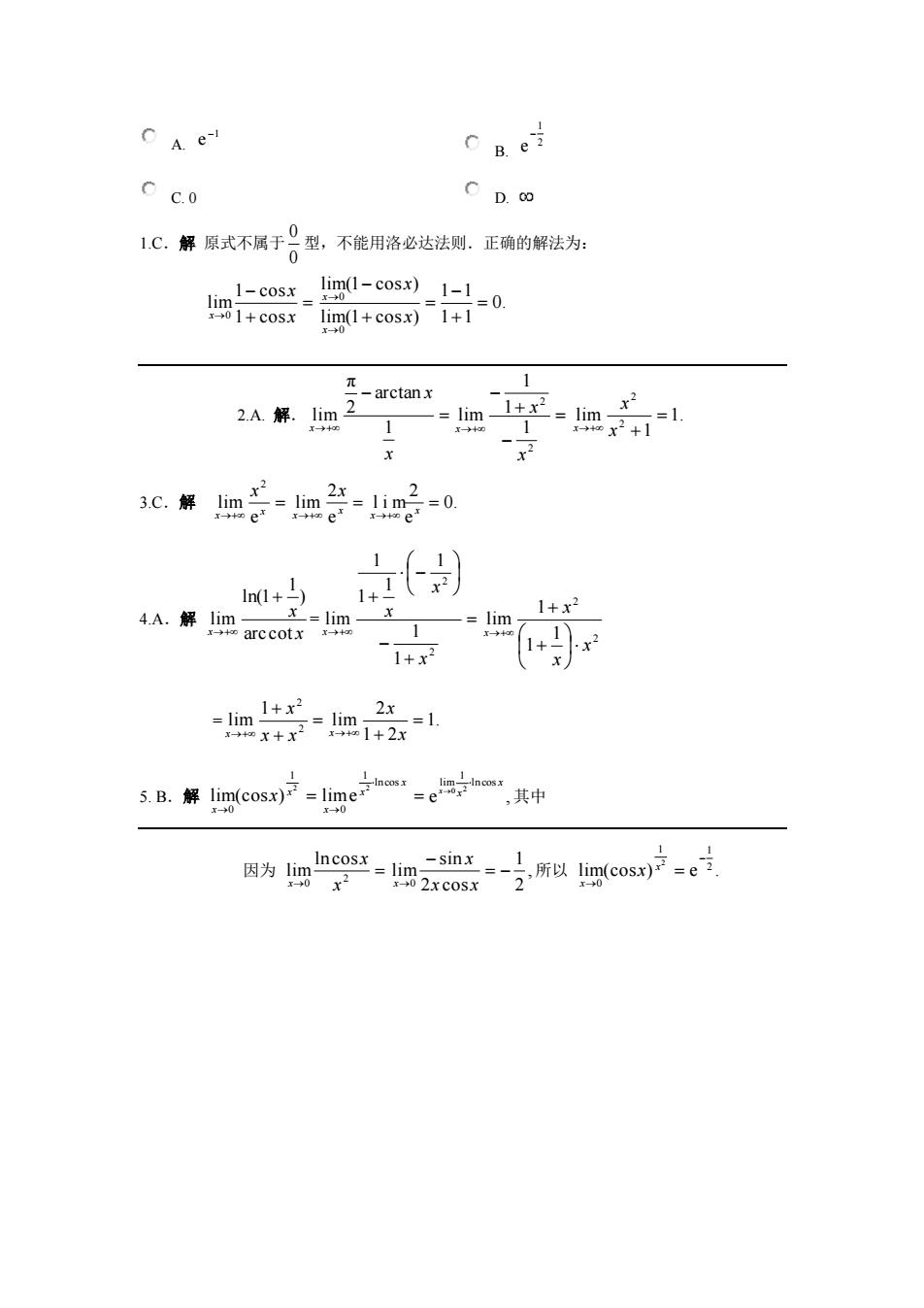
A. B. C. 0 D. 1.C.解 原式不属于 0 0 型,不能用洛必达法则.正确的解法为: x x x 1 cos 1 cos lim 0 0. 1 1 1 1 lim(1 cos ) lim(1 cos ) 0 0 x x x x 2.A. 解. x x x 1 arctan 2 π lim 2 2 1 1 1 lim x x x 1. 1 lim 2 2 x x x 3.C.解 x x x e lim 2 x x x e 2 lim 0. e 2 lim x x 4.A.解 x x x arccot ) 1 ln(1 lim = 2 2 1 1 1 1 1 1 lim x x x x 2 2 1 1 1 lim x x x x = 2 2 1 lim x x x x 1. 1 2 2 lim x x x 5. B.解 2 1 0 lim(cos ) x x x x x x ln cos 1 0 2 lime e , ln cos 1 lim 2 0 x x x 其中 因为 2 0 lncos lim x x x , 2 1 2 cos sin lim 0 x x x x 所以 lim(cos ) e . 2 1 1 0 2 x x x 1 e 2 1 e