
§1一元函数微分学
§1 一元函数微分学

主 录(1-18) 1函数极限的几何解释 2函数的左极限 3x→0时的极限 4X→+0时的极限 5数列的极限 6无穷大 7函数的连续性 8 导数的几何意义 9微分的几何意义 对函数进行全面讨论并画图: 10 y=xe* 11 y=二+4x2 12y= X X (1-x2)2 13 y=arccos x-1 14y= x+1 15 y=x-2arctanx 16y= cos2x cos x 17弧微分ds的几何意义 18曲率
1 函数极限的几何解释 2 函数的左极限 3 x 时的极限 4 x+ 时的极限 5 数列的极限 6 无穷大 7 函数的连续性 8 导数的几何意义 9 微分的几何意义 y xe x 10 17 弧微分ds的几何意义 对函数进行全面讨论并画图: x x y x x y ( x ) x y x x y arccos y = x – 2arctan x x x y cos cos2 11 12 13 14 15 16 主 目 录(1 – 18) 18 曲率

1.函数的极限 Iimf(x)=A的几何解释 x→x0 Vε>0,36>0,当 f(x) y个 0<x-xk6时, A+8 恒有f(x)-A<&. VA的邻域, A 3x的空心6邻域, 该邻域内所有点xA-6 的纵坐标fx)落在 A的ε邻域内, 即相应的点化,fx) 落在绿色区域内. 0 七。-6 Xo x+8 X 合
x y0 f (x ) 0 x A lim f ( x ) A 的几何解释 x x 0 x 0 x 0, 0, 0 | x x0 |δ 时, 当 恒有 f ( x ) A . 该邻域内所有 点 x 的纵坐标 f(x )落在 A 的 邻域 内, 即相应的点 (x,f(x)) 落在绿色区域内 . 1. 函数的极限 A的邻域, x0的空心 邻域 ,A + A –
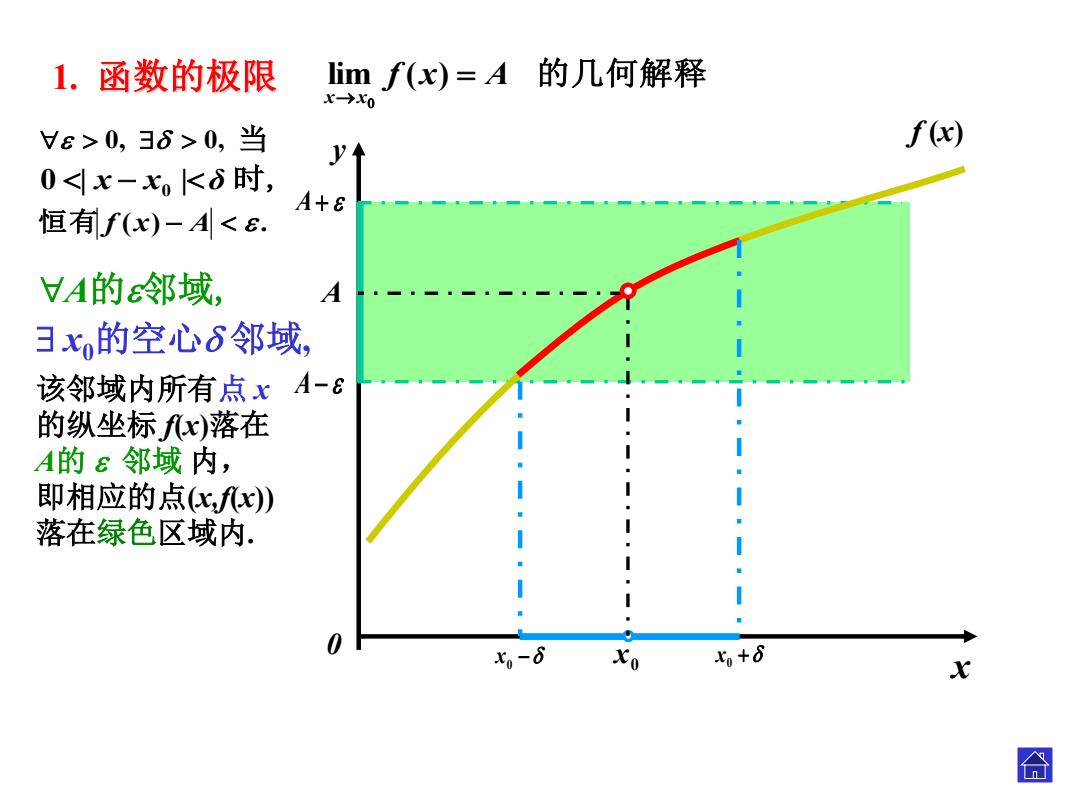
1.函数的极限 Iimf(x)=A的几何解释 x→x0 Vε>0,36>0,当 f(x) y↑ 0<x-xk6时, A+8 恒有f(x)-A<&. VA的邻域, A 3x的空心6邻域, 该邻域内所有点xA-ε 的纵坐标fx)落在 A的ε邻域内, 即相应的点化fx) 落在绿色区域内. 0 七,-6 Xo x+8 X 合
A x y0 0 x A A 0 x 0 x 1. 函数的极限 lim f ( x ) A 的几何解释 x x . f (x ) 该邻域内所有 点 x 的纵坐标 f(x )落在 A 的 邻域 内, 即相应的点 (x,f(x)) 落在绿色区域内 . A 的 邻域 , x0的空心 邻域 , 恒有 f ( x ) A . 0 , 0 , 当 0 | x x 0 | δ 时
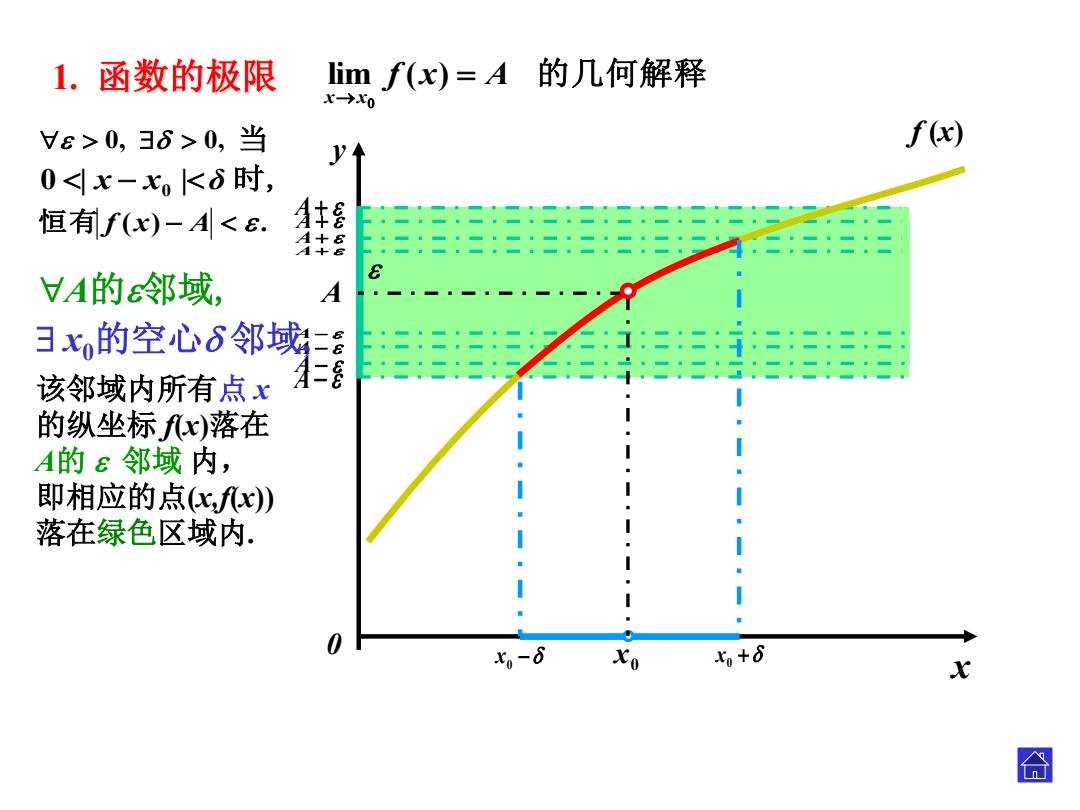
1.函数的极限 Iimf(x)=A的几何解释 x→x0 Vε>0,36>0,当 f(x) 0<x-xoKδ时, 恒有f(x)-A<6.A A+8 VA的s邻域, A ヨx的空心6邻域= 该邻域内所有点x = 的纵坐标fx)落在 A的ε邻域内, 即相应的点,fx) 落在绿色区域内. 0 七,-6 Xo t+6 X 合
A x y0 0 x 0 x 0 x A A A A A A A A 1. 函数的极限 lim f ( x ) A 的几何解释 x x . f (x ) 该邻域内所有 点 x 的纵坐标 f(x )落在 A 的 邻域 内, 即相应的点 (x,f(x)) 落在绿色区域内 . A 的 邻域 , x0的空心 邻域 , 恒有 f ( x ) A . 0 , 0 , 当 0 | x x 0 | δ 时

1.函数的极限 Iimf(x)=A的几何解释 x→xo Vε>0,36>0,当 f(x) y个 0<x-xk6时, 恒有f(x)-A<B. 4+6 VA的邻域, A 3x的空心6邻域,- 该邻域内所有点x 的纵坐标fx)落在 A的8邻域内, 即相应的点,fx) 落在绿色区域内. 0 x。-6 Xo t,+6 X 合
A x y0 0 x A A 0 x 0 x 1. 函数的极限 lim f ( x ) A 的几何解释 x x . f (x ) 该邻域内所有 点 x 的纵坐标 f(x )落在 A 的 邻域 内, 即相应的点 (x,f(x)) 落在绿色区域内 . A 的 邻域 , x0的空心 邻域 , 恒有 f ( x ) A . 0 , 0 , 当 0 | x x 0 | δ 时
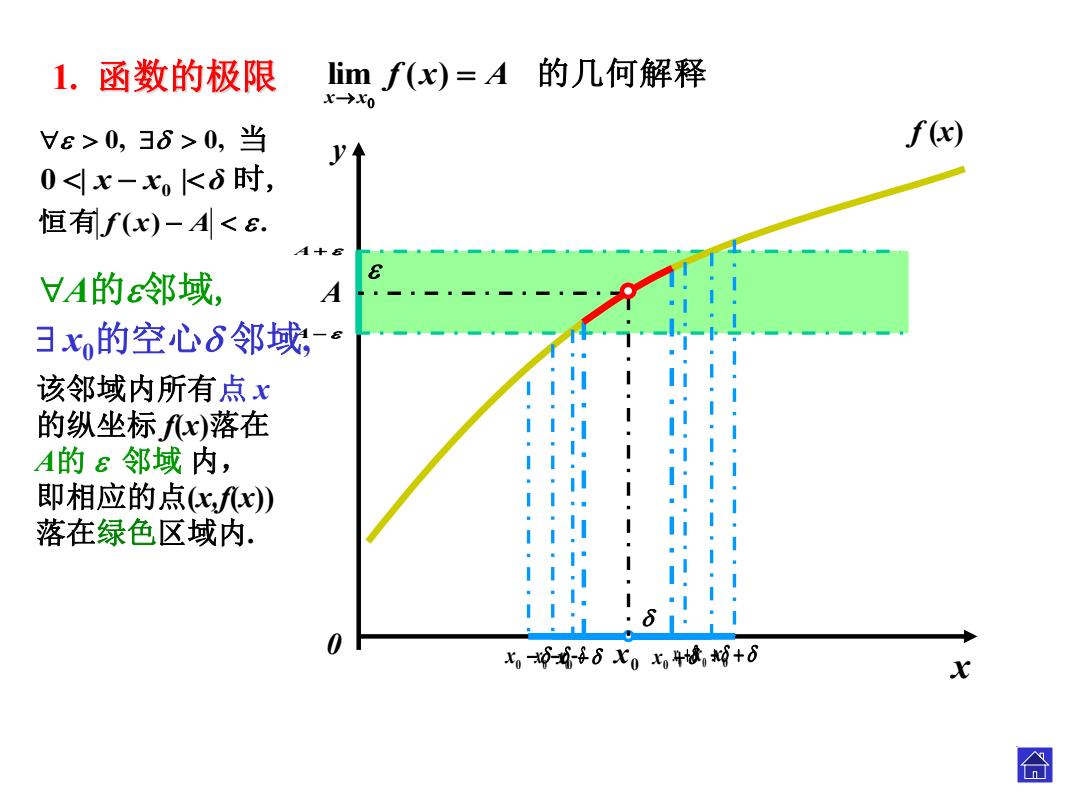
1.函数的极限 limf(x)=A的几何解释 x→xo Vε>0,36>0,当 f(x) y个 0<x-xk6时, 恒有f(x)-A<6. 4+B VA的邻域, A 3x的空心6邻域,-e 该邻域内所有点x 的纵坐标fx)落在 A的8邻域内, 即相应的点fx) 落在绿色区域内. 0 x时斯-母6X0x4城,树+6 X 合
A x y0 0 x A A 0 x 0 x 0 x 0 x 0 x 0 x 0 x 0 x 1. 函数的极限 lim f ( x ) A 的几何解释 x x . f (x ) 该邻域内所有 点 x 的纵坐标 f(x )落在 A 的 邻域 内, 即相应的点 (x,f(x)) 落在绿色区域内 . A 的 邻域 , x0的空心 邻域 , 恒有 f ( x ) A . 0 , 0 , 当 0 | x x 0 | δ 时
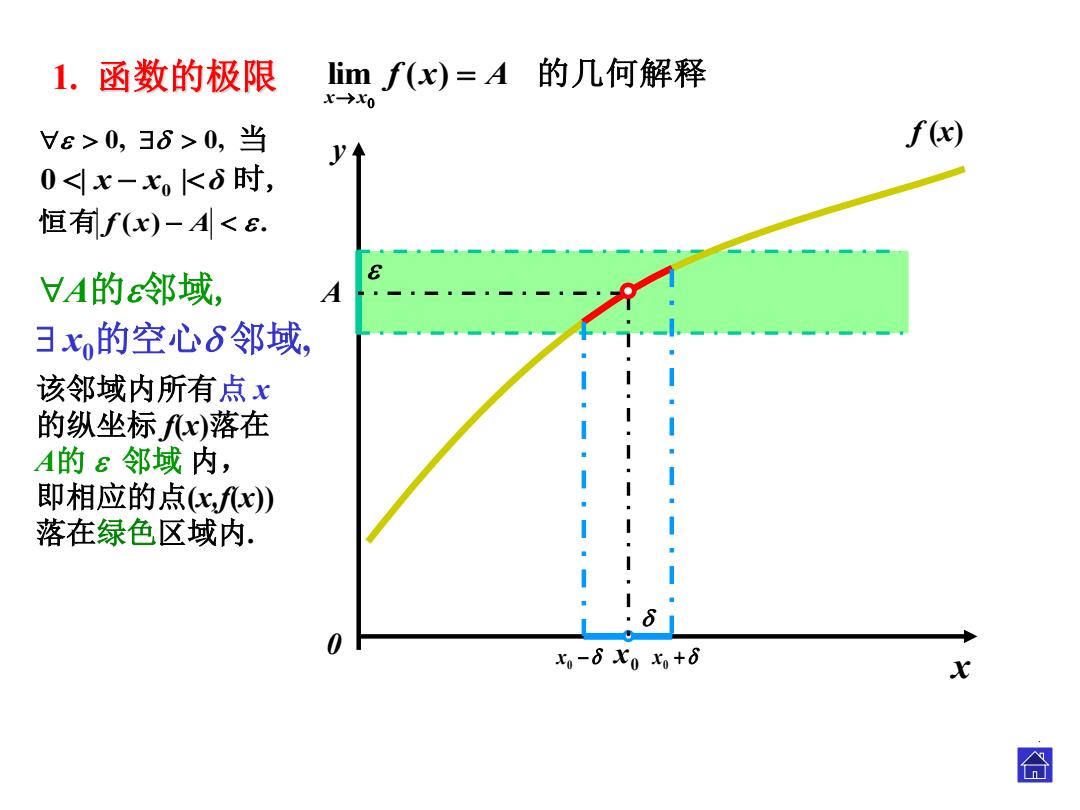
1.函数的极限 Iimf(x)=A的几何解释 x→x0 Vε>0,36>0,当 f(x) y个 0<x-xk6时, 恒有f(x)-A<B. VA的邻域, A 3x的空心6邻域, 该邻域内所有点x 的纵坐标fx)落在 A的ε邻域内, 即相应的点c,x) 落在绿色区域内. 0 x-6X0x+8 X 囧
A x y0 0 x A A 0 x 0 x 1. 函数的极限 lim f ( x ) A 的几何解释 x x . f (x ) 该邻域内所有 点 x 的纵坐标 f(x )落在 A 的 邻域 内, 即相应的点 (x,f(x)) 落在绿色区域内 . A 的 邻域 , 恒有 f ( x ) A . 0 , 0 , 当 x 0的空心 邻域 , 0 | x x 0 | δ 时

1.函数的极限 Iimf(x)=A的几何解释 x→xo Vε>0,36>0,当 f(x) y 0<x-xK6时, 恒有f(x)-A<B. VA的邻域, A 3x的空心6邻域, 该邻域内所有点x 的纵坐标fx)落在 A的8邻域内, 即相应的点,fx) 落在绿色区域内. 0 x-6X0x+8 X 合
A x y0 0 x A A A A A A 0 x 0 x 1. 函数的极限 lim f ( x ) A 的几何解释 x x . f (x ) 该邻域内所有 点 x 的纵坐标 f(x )落在 A 的 邻域 内, 即相应的点 (x,f(x)) 落在绿色区域内 . A 的 邻域 , 恒有 f ( x ) A . 0 , 0 , 当 x 0的空心 邻域 , 0 | x x 0 | δ 时
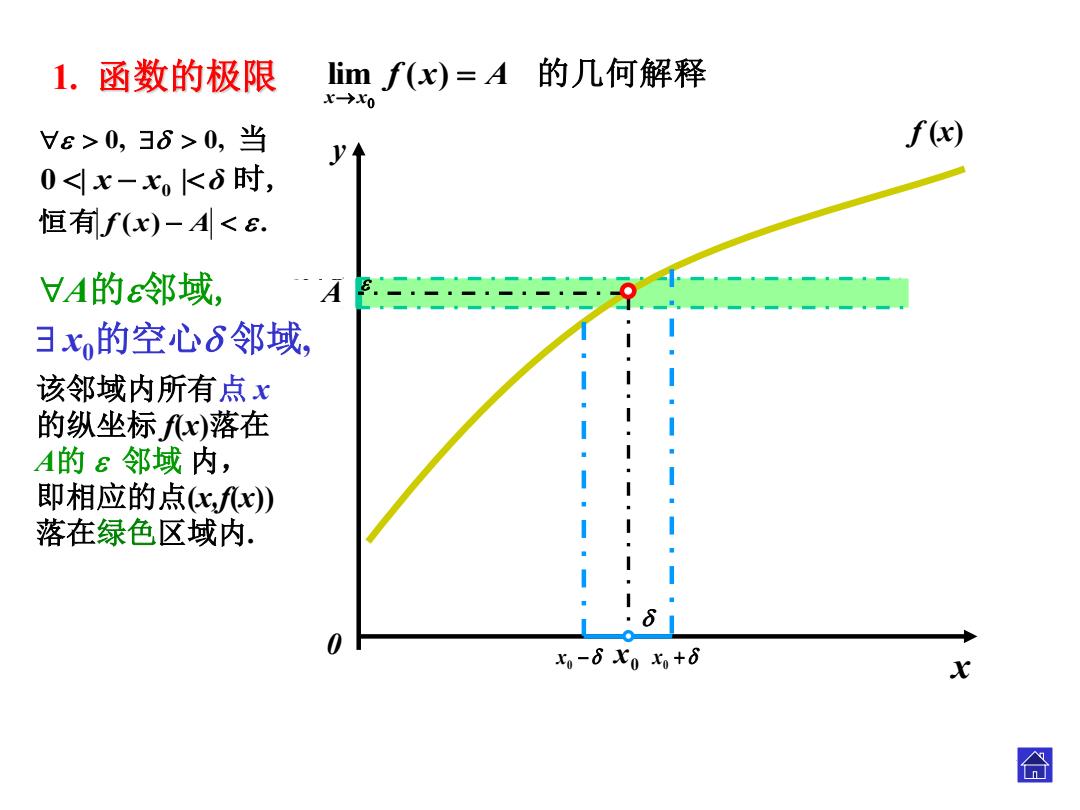
1.函数的极限 Iimf(x)=A的几何解释 x→xo Vε>0,36>0,当 f(x) y 0<x-xK6时, 恒有f(x)-A<B. VA的邻域, A 3x的空心6邻域, 该邻域内所有点x 的纵坐标fx)落在 A的ε邻域内, 即相应的点,fx) 落在绿色区域内. 0 x-6X0x+8 X 合
A x y0 0 x A A 0 x 0 x 1. 函数的极限 lim f ( x ) A 的几何解释 x x . f (x ) 该邻域内所有 点 x 的纵坐标 f(x )落在 A 的 邻域 内, 即相应的点 (x,f(x)) 落在绿色区域内 . A 的 邻域 , x0的空心 邻域 , 恒有 f ( x ) A . 0 , 0 , 当 0 | x x 0 | δ 时