
§ 5 二重积分
§5 二重积分

主目 录(1-25) 1多元函数积分学概况 2曲顶柱体的体积 3比较=∬x+ydo与☑2=J∬(x+yPdo的大小,其中D:(x-22+0y-1P≤2 4二重积分的计算:D是矩形区域 含“复习§2,图19:平行截面面积为已知的立体的体积” 5二重积分的计算:D是曲线梯形区域 6二重积分计算的两种积分顺序 7计算1-∬本yd 其中D:y≤x≤y21≤y≤√3 8用两种顺序计算『dxdy 其中D:y=x与y=x2所围区域 9 求椭圆抛物面z=1- a2 b2 与xoy平面所围成的体积 10将二重积分化成二次积分. D:x+y=1,x-y=1,x=0所围 11将二重积分化成二次积分 D:由四条直线:x=3,x=5,3x-2y+4=0, 与3x-2y+1=0共同围成的区域
4 二重积分的计算:D是矩形区域 含“复习§ 2,图19: 平行截面面积为已知的立体的体积” 5 二重积分的计算:D是曲线梯形区域 6 二重积分计算的两种积分顺序 2 1 2 2 2 2 比较 ( )d 与 ( )d 的大小,其中 :( ) ( ) 2 3 1 I x y σ I x y σ D x y D D 3 1 多元函数积分学概况 2 曲顶柱体的体积 7 : 1 3 2 2 2 x y D y x y y x y y I D 计算 d d 其中 8 用两种顺序计算 xydxdy 其中 D : y x与 y x 2所围区域 D 求椭圆抛物面 与xoy平面所围成的体积 b y a x z 2 2 2 2 9 1 10 将二重积分化成二次积分. D: x+y =1 , x–y =1,x=0所围 11 将二重积分化成二次积分 D: 由四条直线 : x =3,x = 5, 3x –2y+4 = 0, 主 目 录( 1— 25 ) 与 3x –2y+1 = 0 共同围成的区域

12将二重积分换序: I=∫dvfx)d☐ 13将二重积分换序: I(y 14(练习)将二重积分化成二次积分 15 为什么引用极坐标计算二重积分 16利用极坐标计算二重积分 17 怎样用极坐标计算二重积分 (1)极点不在区域D的内部 18怎样用极坐标计算二重积分 (2)极点位于区域D的内部 19 把I=J厂f(x,)dd变为极坐标形式 其中D:(x-a)2+y2=a2与y=0所围区域 20计算I=J∫fxy)dhdy D:x2+y2=1和x2+y2=4之间的环域 21把1=d2fxd变为极坐标形式
16 利用极坐标计算二重积分 17 怎样用极坐标计算二重积分 (1) 极点不在区域 D 的内部 18 怎样用极坐标计算二重积分 (2) 极点位于区域 D 的内部 14 (练习)将二重积分化成二次积分 15 为什么引用极坐标计算二重积分 19 21 把 d ( )d 变为极坐标形式 2 0 2 0 2 R Ry y I y f x,y x 把 ( )d d 变为极坐标形式 D I f x,y x y 其中 D : (x a) 2 y 2 a 2 与 y 0 所围区域 20 计算I f x,y x y D : x 2 y 2 1 和 x 2 y 2 4 之间的环域 D ( )d d 12 将二重积分换序: 1 0 d ( )d y y I y f x,y x 13 将二重积分换序: a ax x x I x f x,y y 0 2 2 d ( )d

22计算I=∬arctan-'drdy D:x2+y2=4,x2+y2=1,y=x,y=0所围第一象限部分 23计算I=∬f(xddD:x2+y=4x,x+y2=8x,x=yy=2x所围 24将积分换序1=dfx■ 25将积分化为极坐标形式1-一d山广f之炒+广g山华炒■
22 arctan D x y x y 计算 I d d I f x,y x y. D 23 计算 ( )d d D : x 2 y 2 4x , x 2 y 2 8x, x y, y 2x所围 . 24 将积分换序 d ( )d 2 0 2 2 2 a ax ax x I x f x,y y 25 将积分化为极坐标形式 R R R R x y x y x f 2 2 2 1 0 y d ( )d x y I R x f R Rx 2 1 0 0 d ( )d 4 1 0 D : x 2 y 2 , x 2 y 2 , y x, y 所围第一象限部分
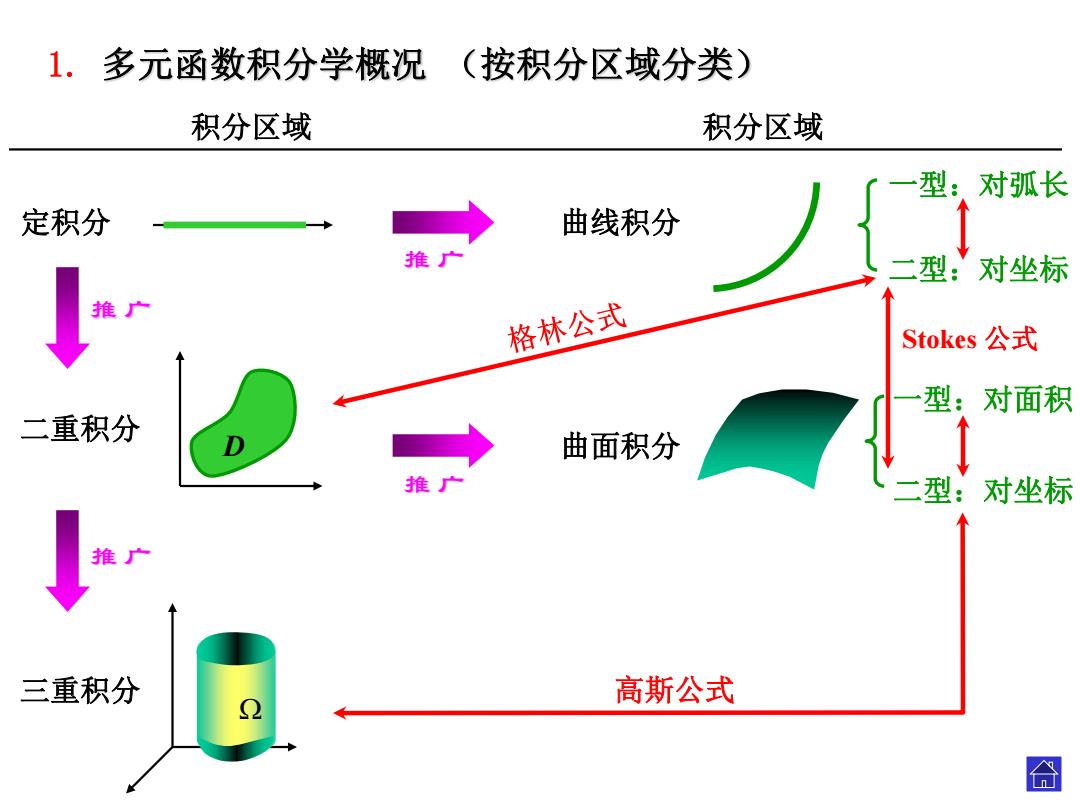
1.多元函数积分学概况 (按积分区域分类) 积分区域 积分区域 型:对弧长 定积分 曲线积分 推, 二型:对坐标 推 格林公式 Stokes公式 型:对面积 二重积分 曲面积分 推 二型:对坐标 推 三重积分 高斯公式 合
(按积分区域分类) 积分区域 积分区域 定积分 二重积分 三重积分 D 曲线积分 曲面积分 一型:对弧长 二型:对坐标 一型:对面积 二型:对坐标 Stokes 公式 高斯公式 1. 多元函数积分学概况 推 广 推 广 推 广 推 广
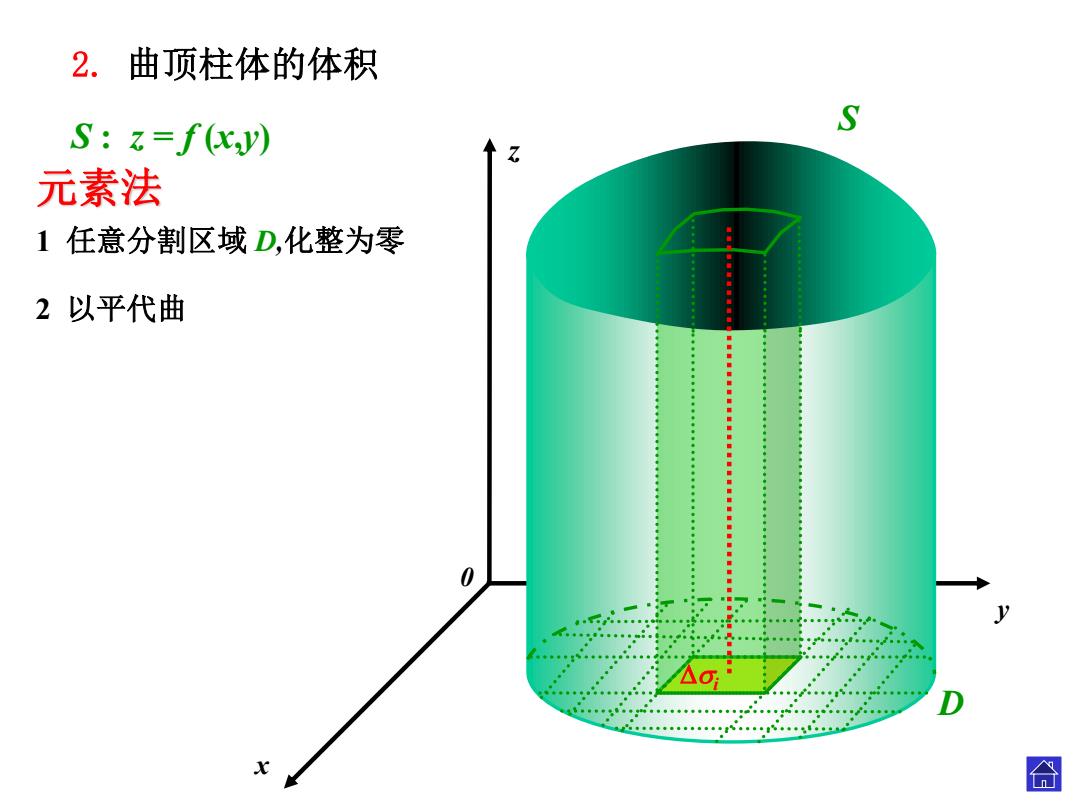
2.曲顶柱体的体积 S:z=f(xy) S 元素法 1任意分割区域D,化整为零 2以平代曲 0 合
x 0 z y D S S : z = f (x,y) 元素法 1 任意分割区域 D,化整为零 2 以平代曲 2. 曲顶柱体的体积 i
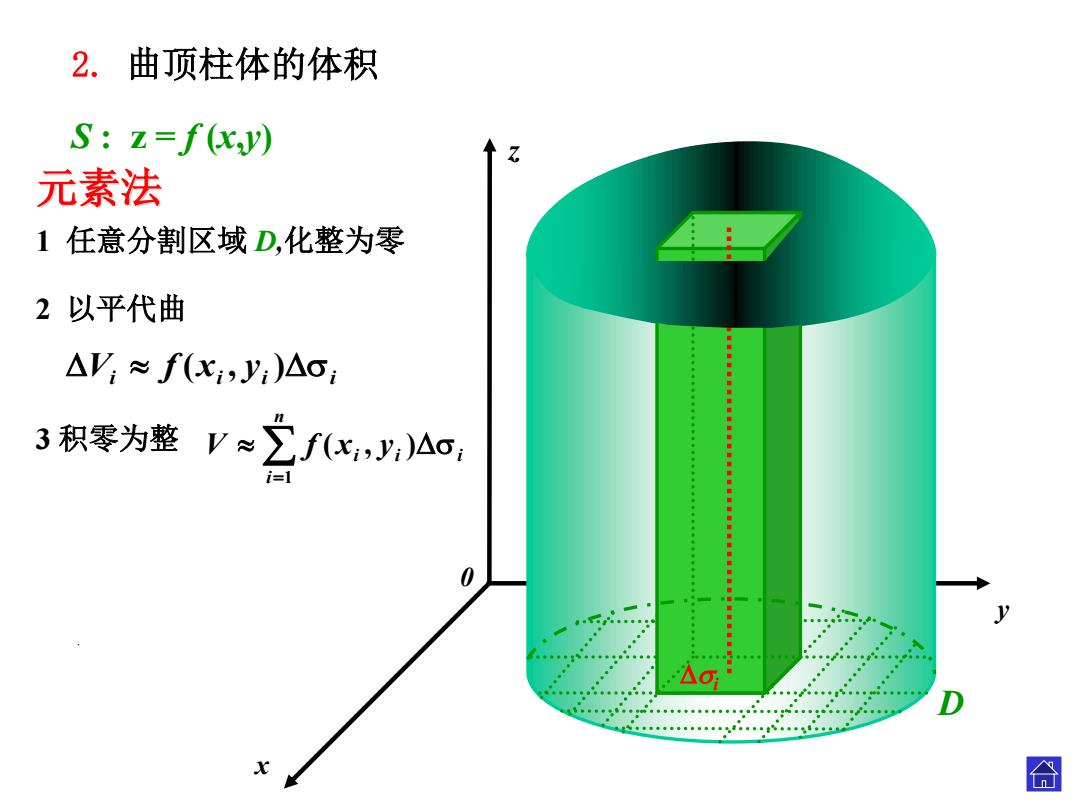
2.曲顶柱体的体积 S:z=f(xy) 元素法 1任意分割区域D,化整为零 2以平代曲 △V:≈f(x,y:)△o: 3积零为整V≈∑fx,,)ao, 0 △ 合
x 0 z y D S : z = f (x,y) i i i i V f (x , y ) 3 积零为整 n i i i i V f x y 1 ( , ) 2 以平代曲 元素法 1 任意分割区域 D,化整为零 2. 曲顶柱体的体积 . i
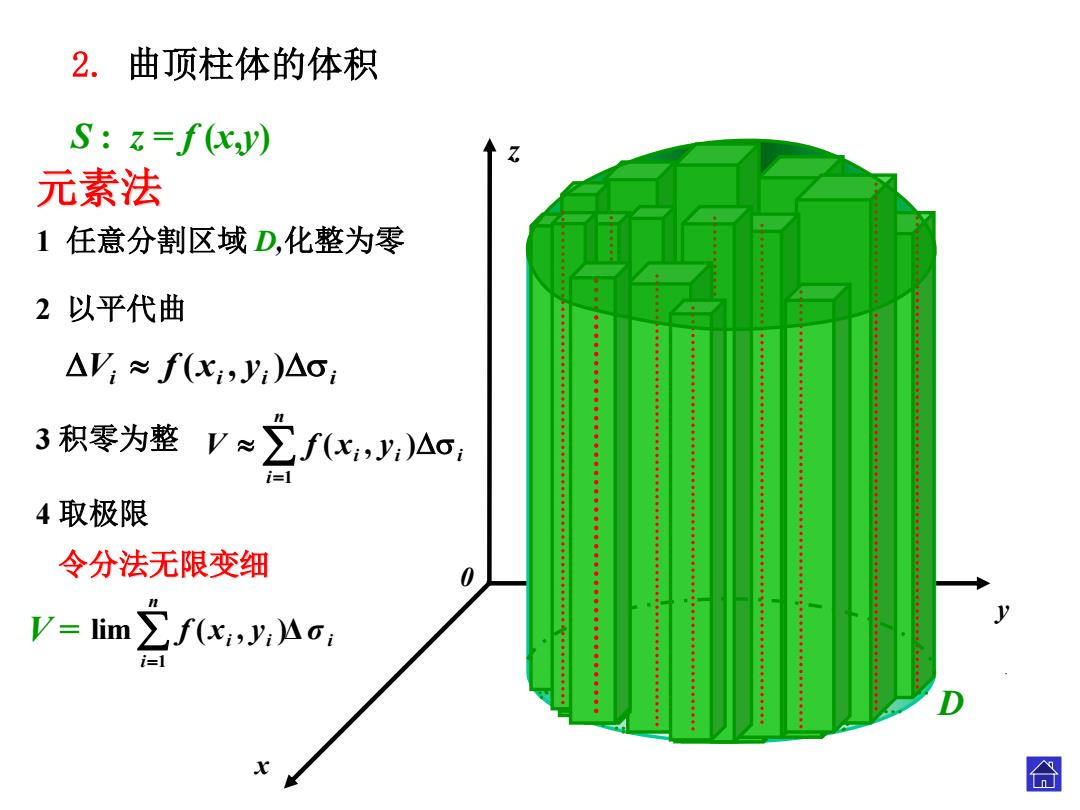
2.曲顶柱体的体积 S:z=f(xy) 元素法 1任意分割区域D,化整为零 2以平代曲 △V;≈f(x,y:)△o: 3积零为整V≈∑fxy,4o; 4取极限 令分法无限变细 0 V=im∑fx,y,Ao; i- 合
x 0 z y D S : z = f (x ,y ) i i i i V f ( x , y ) 3 积零为整 n i i i i V f x y 1 ( , ) 4 取极限 令分法无限变细 i 2 以平代曲 元素法 1 任意分割区域 D,化整为零 2. 曲顶柱体的体积 . ni i i σ i f x y 1 V = lim ( , )Δ
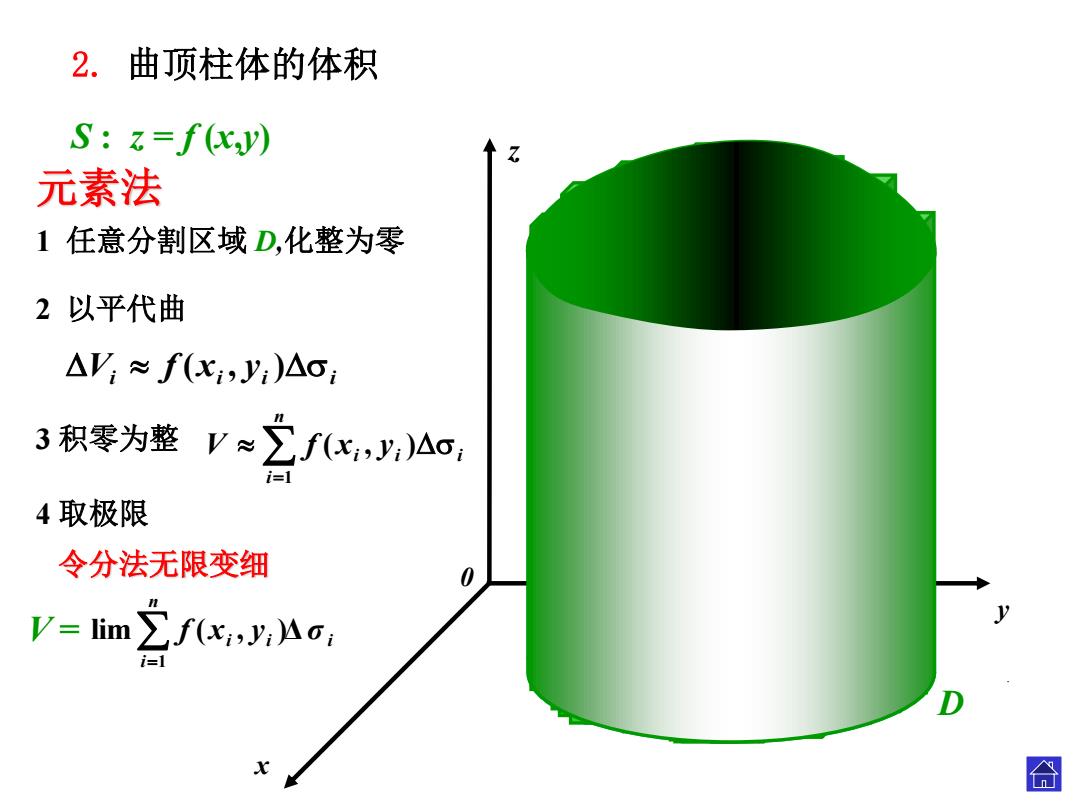
2.曲顶柱体的体积 S:z=f(xy) 元素法 1任意分割区域D,化整为零 2以平代曲 △V≈f(xy:)△o: 3积零为整V≈∑fx,,Ac 4取极限 令分法无限变细 0 V=lim∑fxy,Ao; 合
x 0 z y D S : z = f (x ,y ) i i i i V f ( x , y ) 3 积零为整 i ni i i i V f x y 1 ( , ) 4 取极限 令分法无限变细 2 以平代曲 元素法 1 任意分割区域 D,化整为零 2. 曲顶柱体的体积 . ni i i σ i f x y 1 V = lim ( , )Δ
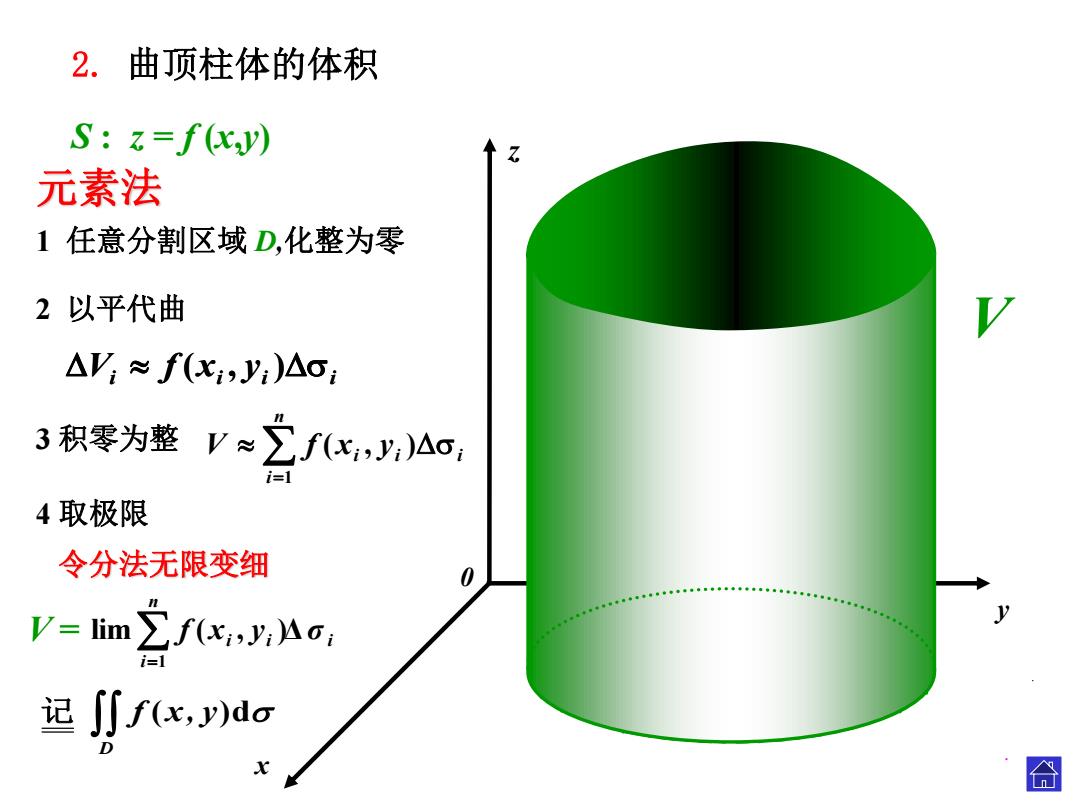
2.曲顶柱体的体积 S:z=f(xy) 元素法 1任意分割区域D,化整为零 2以平代曲 △V≈f(x,y)△o: 3积零为整V≈∑fx,,Ac 4取极限 令分法无限变细 0 V=lim∑fx,y,Aa, 记Jjf(x,y)do 囧
x 0 z y S : z = f (x ,y ) i i i i Vi f ( x i , y i ) i V f ( x , y ) 3 积零为整 4 取极限f (x, y)d D 记 令分法无限变细 2 以平代曲 V 元素法 1 任意分割区域 D,化整为零 . 2. 曲顶柱体的体积 . ni i i σ i f x y 1 V = lim ( , )Δ n i i i i V f x y 1 ( , )