
§3 空间解析几何
§3 空间解析几何

主 目 录(1-30) 1 空间直角坐标系 2 两矢量和在轴上的投影 3 矢量积的分配律的证明 4 混合积的几何意义 5 一般柱面F(x,y)=0 6 一般柱面Fyz)=0 7 椭圆柱面 8 双曲柱面 9抛物柱面 10 旋转面的方程 11双叶旋转双曲面 12 单叶旋转双曲面 13 旋转锥面 14 旋转抛物面 15环面 16 椭球面 17椭圆抛物面 18 双曲抛物面 19双曲面的渐近锥面 20 单叶双曲面是直纹面 21双曲抛物面是直纹面 2 一般锥面 23空间曲线—圆柱螺线 24 空间曲线在坐标面上的投影 25空间曲线作为投影柱面的交线(1) 26空间曲线作为投影柱面的交线(2) 27作出平面y=0,=0,3x+y=6,3x+2y=12和x+y+z=6所围成的立体图形
1 空间直角坐标系 2 两矢量和在轴上的投影 3 矢量积的分配律的证明 4 混合积的几何意义 5 一般柱面 F(x,y)=0 6 一般柱面 F(y,z)=0 7 椭圆柱面 8 双曲柱面 9 抛物柱面 10 旋转面的方程 11 双叶旋转双曲面 12 单叶旋转双曲面 13 旋转锥面 14 旋转抛物面 15 环面 16 椭球面 17 椭圆抛物面 18 双曲抛物面 19 双曲面的渐近锥面 20 单叶双曲面是直纹面 21 双曲抛物面是直纹面 22 一般锥面 23 空间曲线——圆柱螺线 24 空间曲线在坐标面上的投影 25 空间曲线作为投影柱面的交线(1) 26 空间曲线作为投影柱面的交线(2) 27 作出平面y=0 , z=0,3x+y =6, 3x+2y =12 和 x+y+z = 6所围成的立体图形 主 目 录( 1— 30 )

28 作出曲面x2+y2=a?x2+z2=a2,x=0,y=0,z=0所围立体 图形 29 作出曲面z=1-Vx2+y2和x2+y2-2=1所围立体图形 3 30平面x=a,y=a,z=a,x+y+z=。a在第一卦限所围立体图形
28 图形 作出曲面x 2 y 2 a,2 x 2 z 2 a 2 , x 0, y 0,z 0所围立体 29 平面 x a, y a,z a, x y z a 在第一卦限所围立体图形 30 . 1 1 作出曲面 z x 2 y 2 和 x 2 y 2 z 所围立体图形
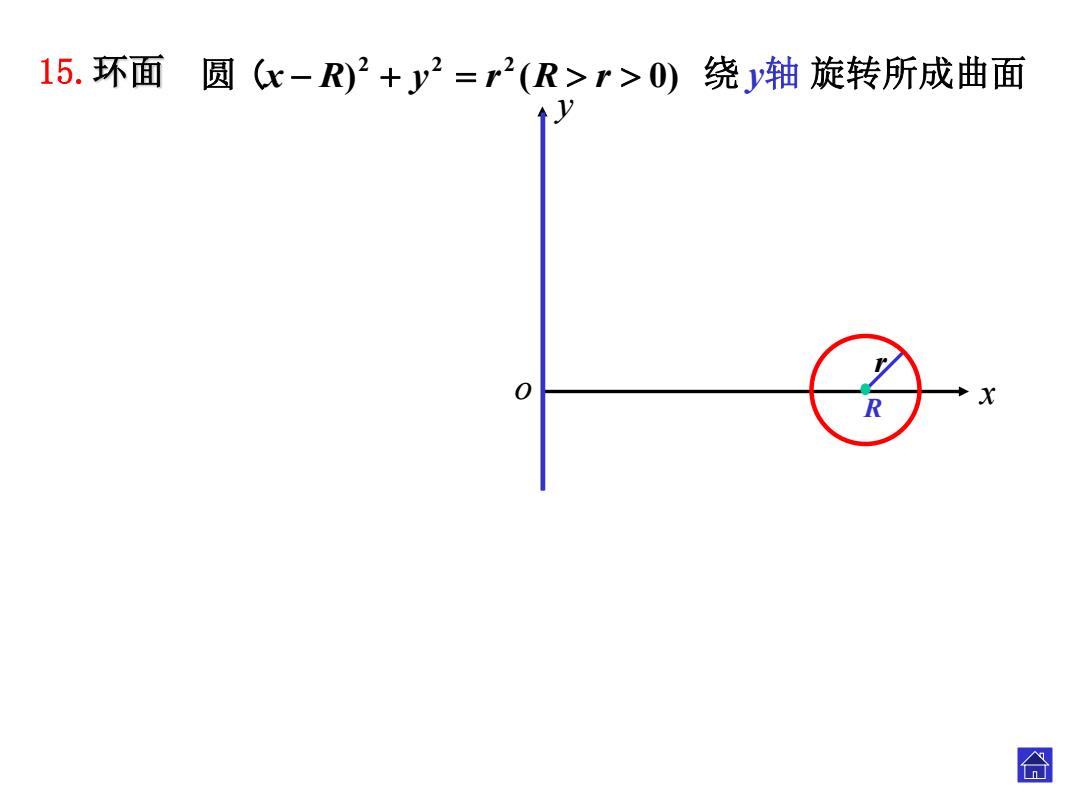
15.环面圆(x-R)2+y2=r2(R>r>0)绕y轴旋转所成曲面 0 R X 合
15.环面 y o x r R ) ( 0) 2 2 2 圆 (x R y r R r 绕 y轴 旋转所成曲面
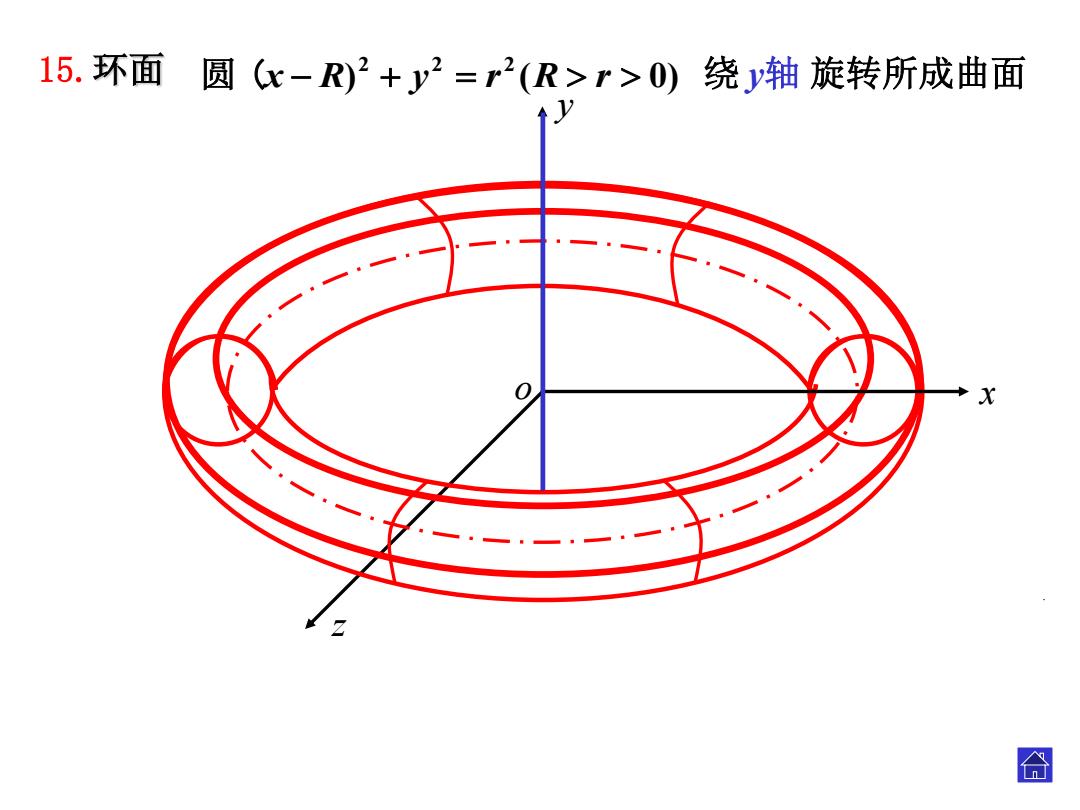
15.环面圆(x-R)2+y2=r2(R>r>0) 绕y轴旋转所成曲面 0 X 合
15.环面 z 绕 y轴 旋转所成曲面 y o x . ) ( 0) 2 2 2 圆 (x R y r R r
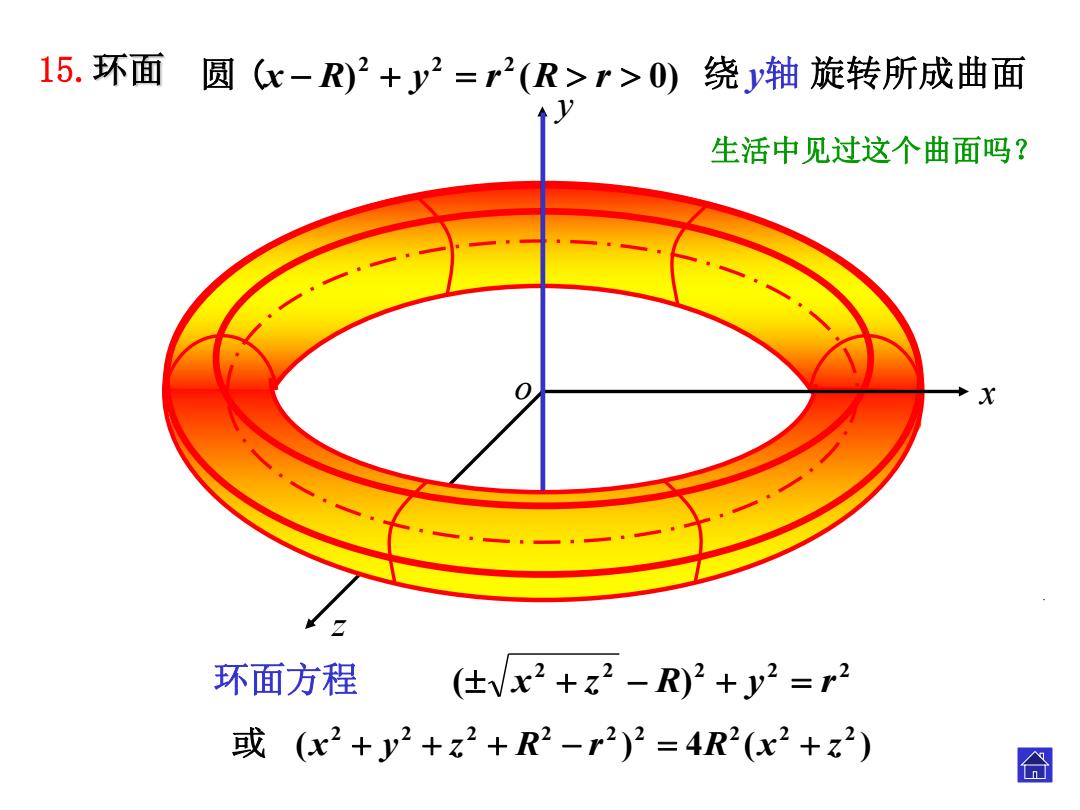
15.环面圆(x-R)2+y2=r2(R>r>0)绕y轴旋转所成曲面 生活中见过这个曲面吗? 0 X 环面方程 (仕Vx2+z2-R)2+y2=r2 或(x2+y2+z2+R2-r2)2=4R2(x2+z2) 合
15.环面 z 绕 y轴 旋转所成曲面 2 2 2 2 2 环面方程 ( x z R) . y r 生活中见过这个曲面吗? y o x ( ) 4 ( ) 2 2 2 2 2 2 2 2 2 或 x y z R r R x z . . ) ( 0) 2 2 2 圆 (x R y r R r

15.环面 救生圈 合
救生圈 . 15.环面
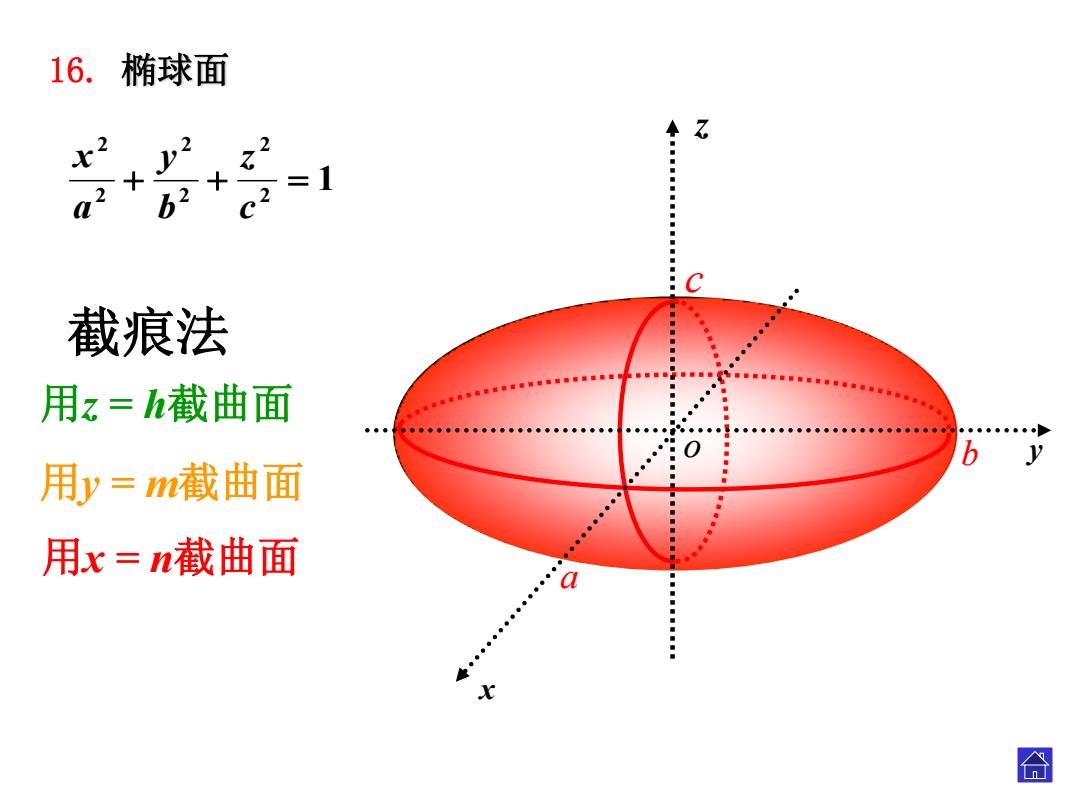
16.椭球面 Z 632 =1 C 截痕法 ■■ 用z=h截曲面 b 用y=m截曲面 用x=n截曲面 a 合
1 22 22 22 cz by ax 截痕法 用z = h截曲面 用y = m截曲面 用x = n截曲面 a b c y x zo 16. 椭球面
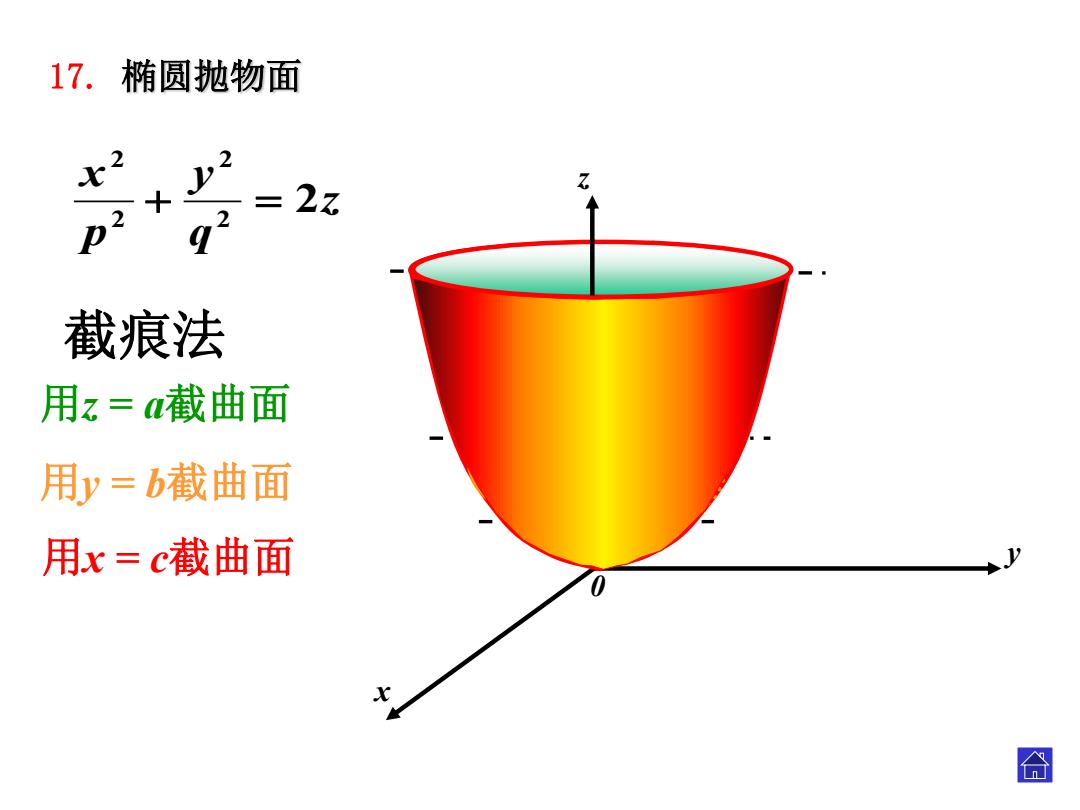
17.椭圆抛物面 少 = 2 23 1 截痕法 用z=截曲面 用y=b截曲面 用x=c截曲面 合
x z y 0 截痕法 用z = a截曲面 用y = b截曲面 用x = c截曲面 17. 椭圆抛物面 z qy px 2 22 22
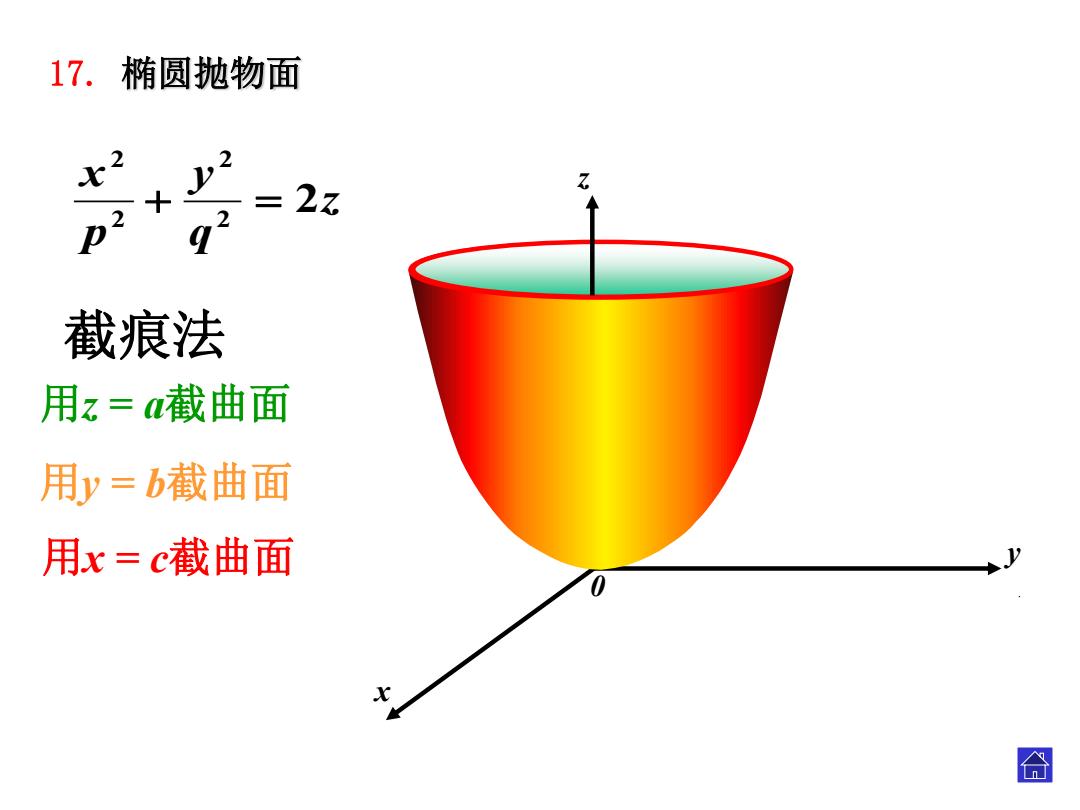
17.椭圆抛物面 2 少2 =1 3 2 91 截痕法 用z=截曲面 用y=b截曲面 用x=c截曲面 0 合
x z y 0 截痕法 用z = a截曲面 用y = b截曲面 用x = c截曲面 17. 椭圆抛物面 . z qy px 2 22 22