
§2- 一元函数积分学
§2 一元函数积分学
主目 录(1-25)》 1曲边梯形的面积 2求曲线y2=2x与y=x-4围成的面积 3 求抛物线y=-x2+4x-3与其在点(0,-3)和点(3,0)处的切线所围 成图形的面积 4 曲边扇形的面积 5 旋轮线 6 旋轮线也叫摆线 7 旋轮线是最速降线 8 心形线 9星形线 10 圆的渐伸线 11笛卡儿叶形线 12 双纽线 13 阿基米德螺线 14 双曲螺线 15 求曲线r=3Cos0及r=1+cos0分别所围成的图形的公共部分的 面积 16 求曲线r=√2sin0及r2=cos20分别所围成的图形的公共部分的面 积
5 旋轮线 6 旋轮线也叫摆线 7 旋轮线是最速降线 8 心形线 9 星形线 10 圆的渐伸线 11 笛卡儿叶形线 12 双纽线 13 阿基米德螺线 14 双曲螺线 主 目 录(1–25 ) 15 16 面积 求曲线 r 3cosθ 及 r 1 cos θ 分别所围成的图形的公共部分的 积 求曲线 r 2sinθ 及 r 2 cos2 θ 分别所围成的图形的 公共部分的面 2 求曲线 2 与 4 围成的面积 2 y x y x 3 成图形的面积 求抛物线 y x 2 4x 3 与其在点(0,3)和点(3,0)处的 切线所围 1 曲边梯形的面积 4 曲边扇形的面积

17圆p≤1被心形线p=1+cos0分割为两部分,求这两部分的面积。 18 求由双纽线(x2+y2)2=a2(x2-y2)所围而且在圆周x2+y2= 2 内部的面积。 19平行截面面积为己知的立体的体积。 20半径为R的正圆柱体被通过其底的直径并与底面成a角的平面所截,得 一圆柱楔。求其体积。 21求以半径为R的圆为底,平行且等于底圆直径的线段为顶,高为的正 劈锥体的体积。■ 22旋转体体积(y=f(x)绕x轴) 23旋转体体积(x=g(6y)绕轴)■ 24旋转体体积(柱壳法) 25旋转体的侧面积 ■
19 平行截面面积为已知的立体的体积。 20 半径为R的正圆柱体被通过其底的直径并与底面成角的平面所截,得 一圆柱楔。求其体积。 21 求以半径为R的圆为底,平行且等于底圆直径的线段为顶,高为h的正 劈锥体的体积。 22 旋转体体积(y =f(x)绕x轴) 23 旋转体体积(x =g(y)绕y轴) 24 旋转体体积(柱壳法) 25 旋转体的侧面积 18 17 圆ρ 1被心形线 ρ 1 cosθ 分割为两部分,求这两 部分的面积。 求由双纽线 ( ) ( ) 2 2 2 2 2 2 2 2 2 2 a x y a x y 所围而且在圆周 x y 内部的面积。
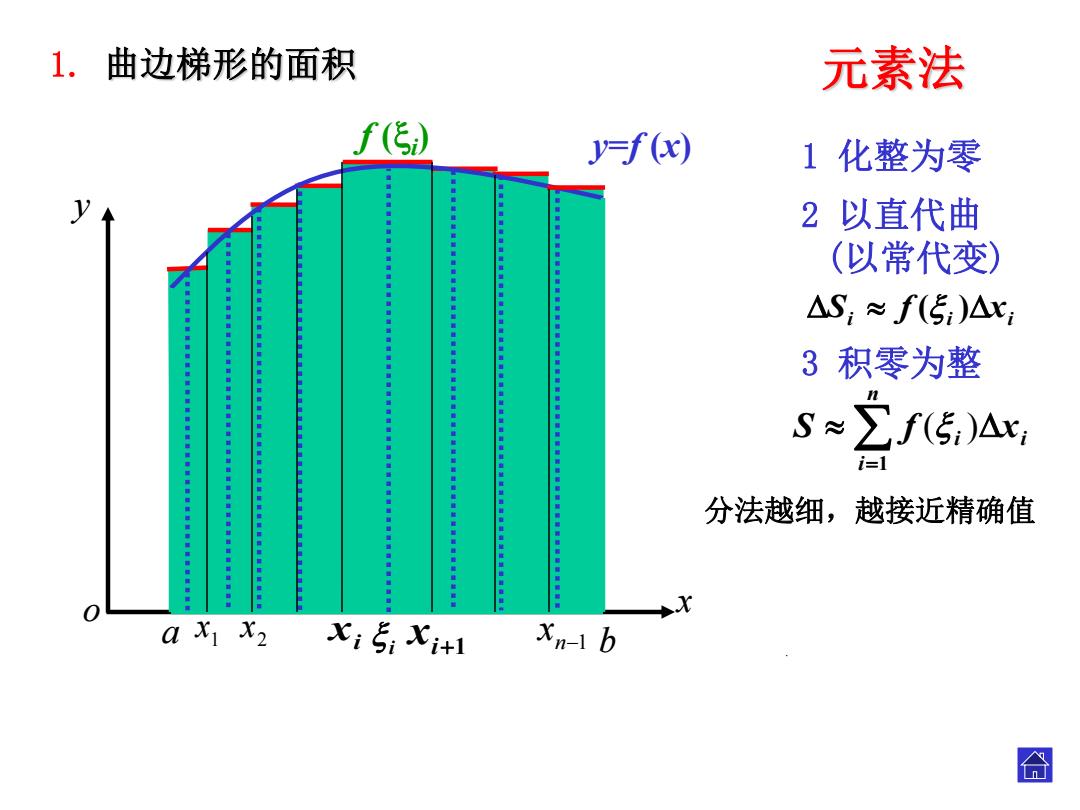
1.曲边梯形的面积 元素法 f(传) =f(x) 1化整为零 2以直代曲 (以常代变) △S:≈f(5:)△c; 3积零为整 S≈∑f(5;)△x: i=1 分法越细,越接近精确值 0 a x x2xix+ Xn-1 b 合
xi xi1 1 x i 2 x 元素法 1 化整为零 2 以直代曲 (以常代变) i i xi S f ( ) 3 积零为整 y o x y=f (x) n1 x n i i xi S f 1 ( ) a b . . 分法越细,越接近精确值 1. 曲边梯形的面积 f (i )
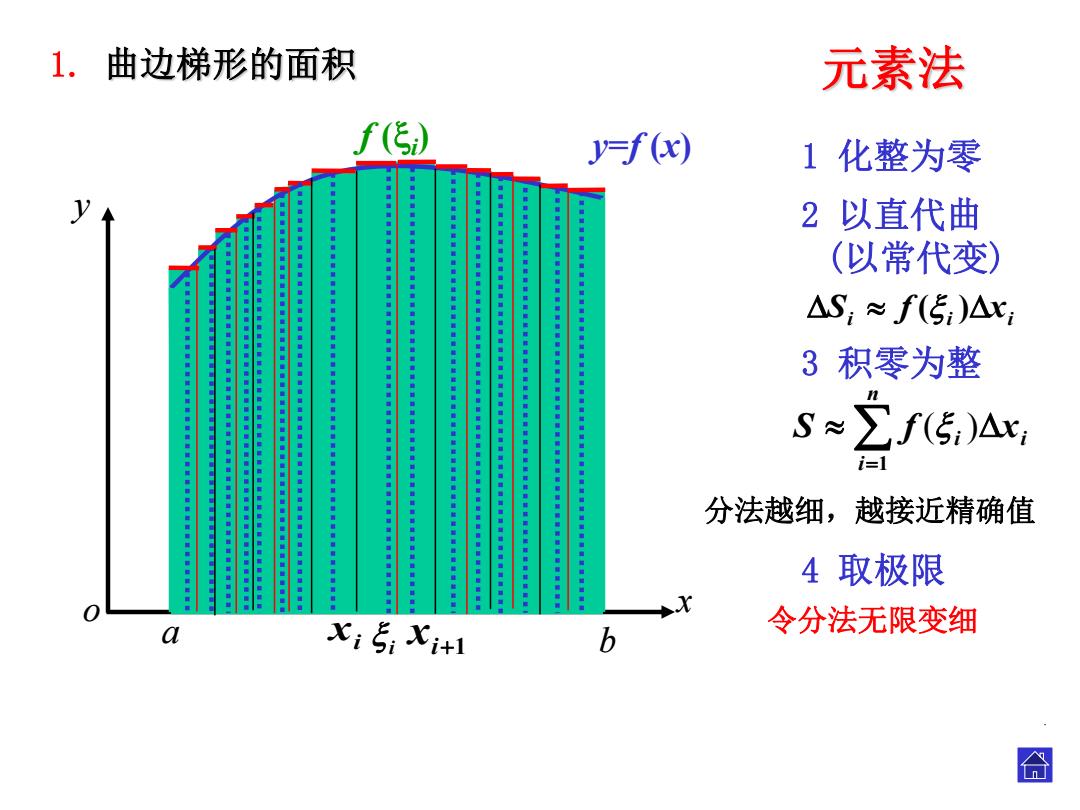
1.曲边梯形的面积 元素法 f(5) y=f(x) 1化整为零 2以直代曲 (以常代变) : △S:≈f(5:)△x: 3积零为整 S≈∑f(5)△x: i=1 : 分法越细,越接近精确值 4取极限 令分法无限变细 合
xi i xi1 元素法 4 取极限 y o x y=f (x) 令分法无限变细 . a . b . . 分法越细,越接近精确值 1 化整为零 2 以直代曲 (以常代变) 3 积零为整 n i i xi S f 1 ( ) i i xi S f ( ) 1. 曲边梯形的面积 . f (i )
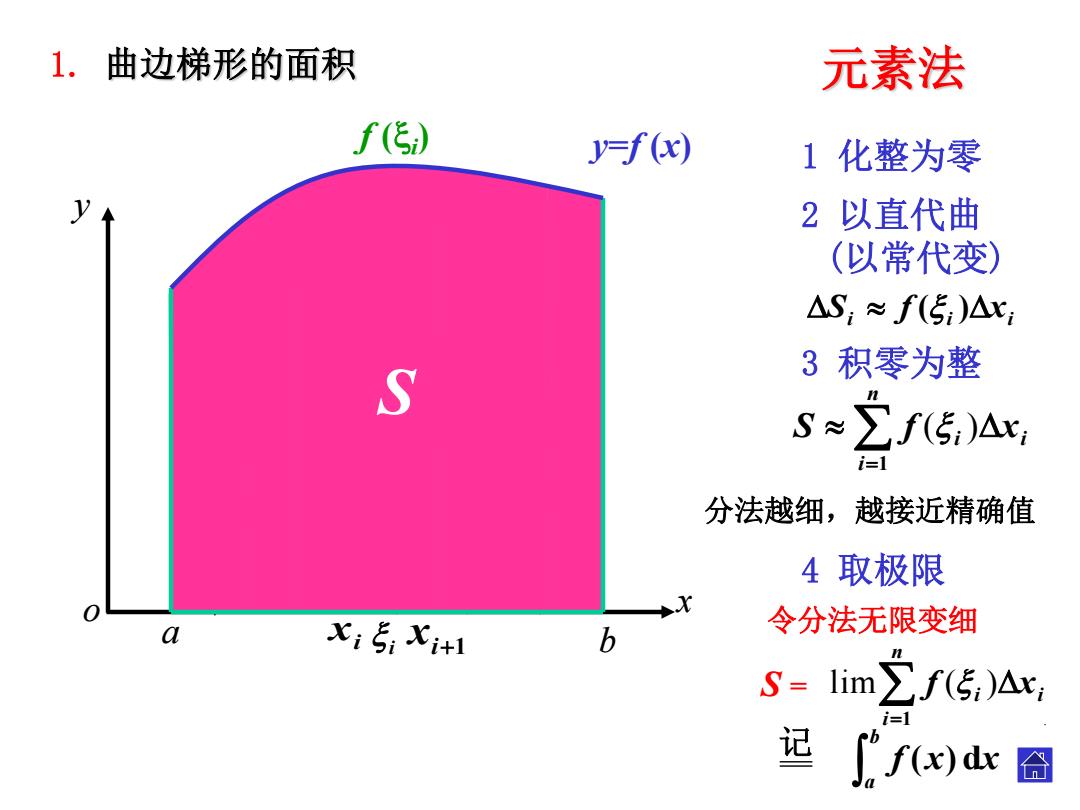
1.曲边梯形的面积 元素法 f(5) y=f(x) 1化整为零 2以直代曲 (以常代变) △S:≈f(5:)△c: S 3积零为整 S≈∑f(5:)△, i=1 分法越细,越接近精确值 4取极限 0 a XiXi+1 令分法无限变细 b S=lim∑f传:)Ax, i=1 ∫fx)dc圆 记
xi i xi1 元素法 4 取极限 y o x y=f (x) 令分法无限变细 . . . . 分法越细,越接近精确值 1 化整为零 2 以直代曲 (以常代变) 3 积零为整 n i i xi S f 1 ( ) i i xi S f ( ) 1. 曲边梯形的面积 . f (i ) n i i xi f 1 lim ( ) 记 S = . b a f (x)dx S . a b
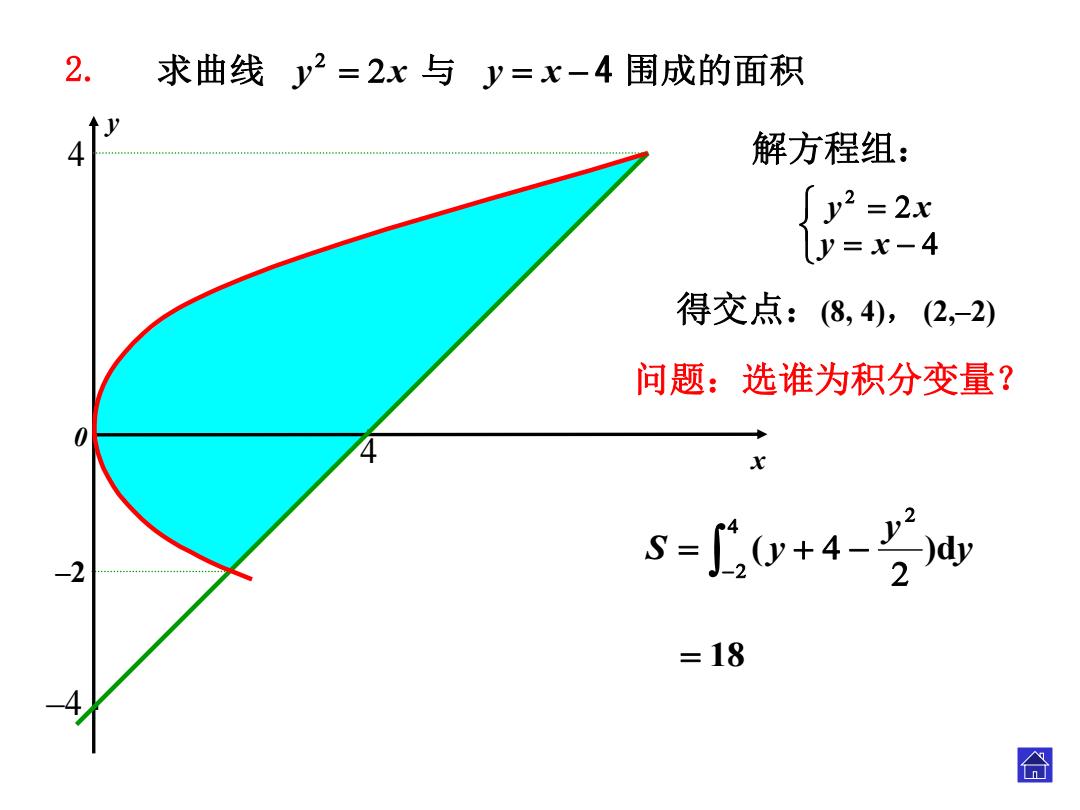
2. 求曲线y2=2x与y=x-4围成的面积 4 解方程组: 2 得交点:(⑧,4),(2,-2) 问题:选谁为积分变量? 0 4 -2 s=小0+4-2 =18 合
求曲线 与 4 围成的面积 y x y x –2 。 。 0 y x 2. 4 4 –4 解方程组: y x y x 得交点:(8, 4), (2,–2) 问题:选谁为积分变量? ( )dy y S y 18
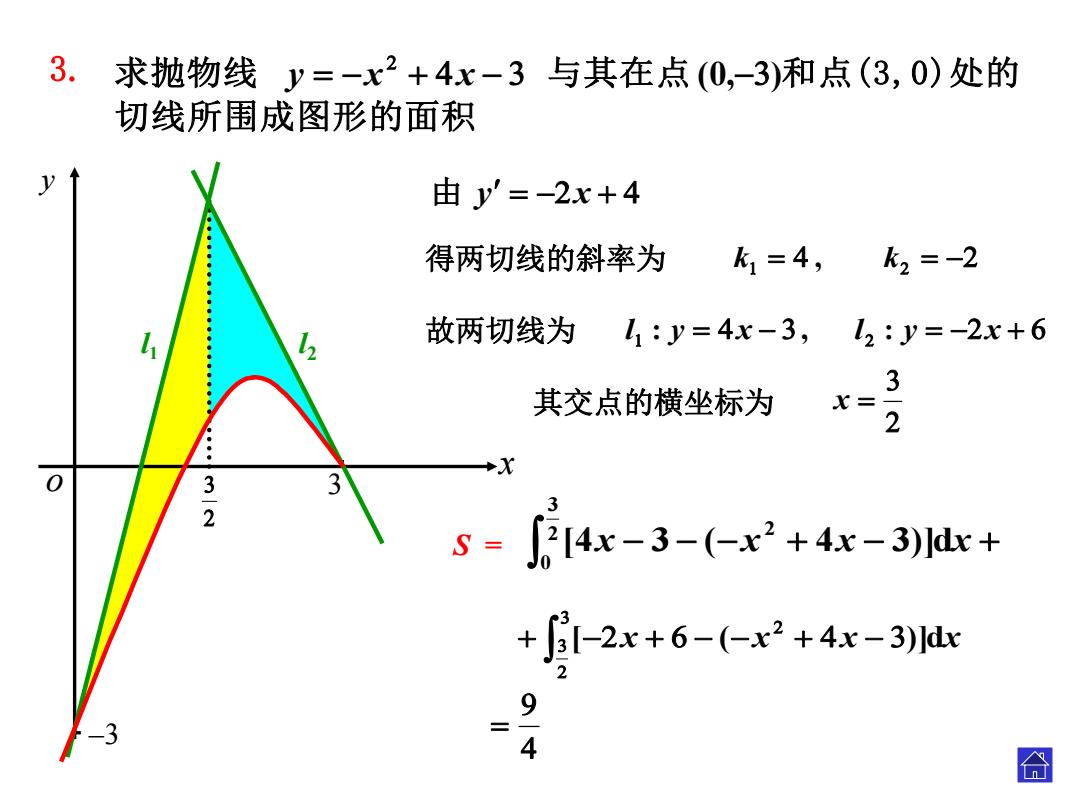
3.求抛物线y=-x2+4x-3与其在点(0,-3)和点(3,0)处的 切线所围成图形的面积 y 由y'=-2x+4 得两切线的斜率为 k1=4,k2=-2 2 故两切线为 11:y=4x-3,2:y=-2x+6 其交点的横坐标为 x= 2 -x 0 3-2 3 3 s=J2[4x-3-(-x2+4x-3)x+ +1-2.x+6-(←x2+4r-3mx 9 -3 合
切线所围成图形的面积 求抛物线 与其在点 (0,)和点(3,0)处的 y x x 。 。 3. x y o 3 –3 由 y x 得两切线的斜率为 , k 故两切线为 : , l y x 其交点的横坐标为 x [x (x x )]dx 。 k l : y x [4 3 ( 4 3)]d 2 2 3 0 S = x x x x l1 l2
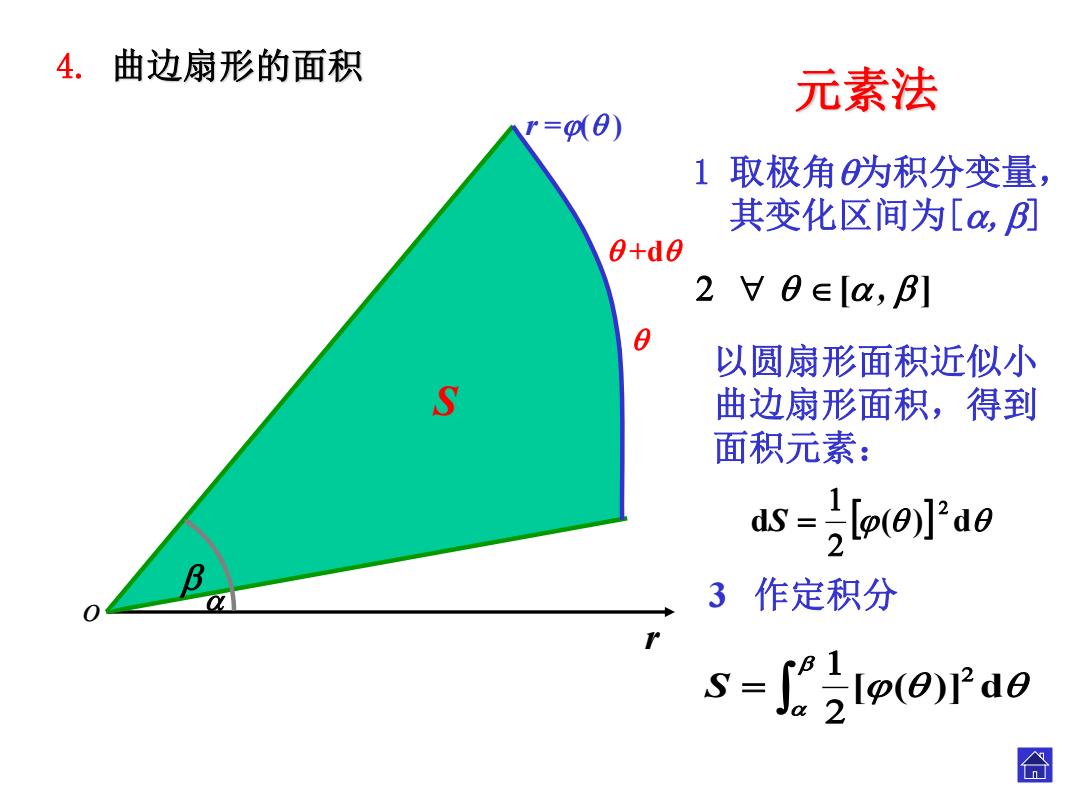
4.曲边扇形的面积 元素法 r=d0) 1取极角为积分变量, 其变化区间为[a,例 0+d0 2廿0∈[a,B] 0 以圆扇形面积近似小 S 曲边扇形面积,得到 面积元素: ds=2le(o]Pd0 3作定积分 s-rae 合
d o +d r =( ) 元素法 1 取极角为积分变量, 其变化区间为[,] d ( ) d S 以圆扇形面积近似小 曲边扇形面积,得到 面积元素: [ , ] . . S [( )] d 4. 曲边扇形的面积 dS S 3 作定积分 . r

5.旋轮线 一圆沿直线无滑动地滚动,圆上任一点所画出的曲线。 0… X 合
x a 圆上任一点所画出的曲线。 5. 旋轮线 一圆沿直线无滑动地滚动