
§4多元函数微分学
§4 多元函数微分学

主目 录1-8) 1二重极限存在的例子 2二重极限不存在的例子■ 3偏导数的几何意义 含复习一元函数导数 4全微分的几何意义 含复习一元函数微分 5 方向导数 6 七框图 7多元函数的极值 ■ y(x2-y2, (x,y)≠(0,0) 8 二元函数 f(x,)=x2+y2 0 (x,y)=(0,0) 的图形,该函数f(0,0)=1而 f"(0,0)=-1
的图形,该函数 8 0 , ( ) (0,0) ( ) (0,0) 2 2 2 2 x,y , x,y x y xy ( x y ) f ( x, y ) f xy (0,0) 1 f yx (0,0) 1 二元函数 而 1 二重极限存在的例子 2 二重极限不存在的例子 3 偏导数的几何意义 含复习一元函数导数 4 全微分的几何意义 含复习一元函数微分 5 方向导数 6 七框图 7 多元函数的极值 主 目 录(1—8)
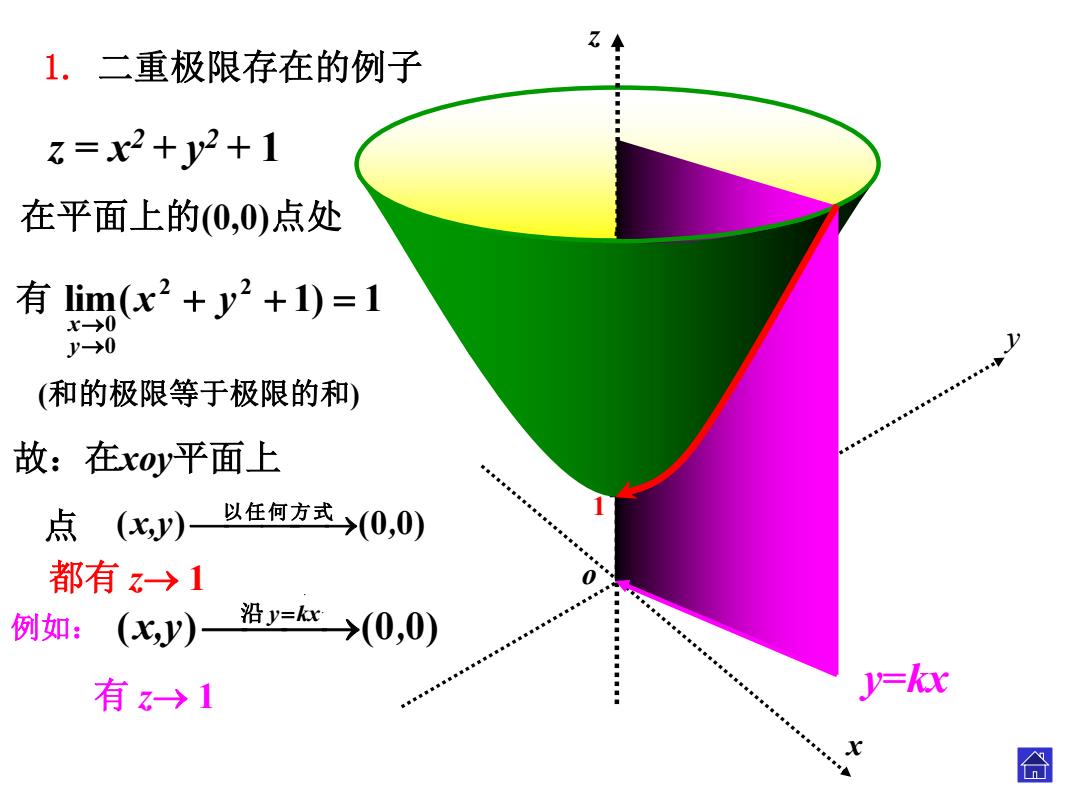
Z 1.二重极限存在的例子 : z=x2+y2+1 在平面上的(0,0)点处 有im(x2+y2+1)=1 x→0 y→0 (和的极限等于极限的和) 故:在oy平面上 点(Ky) 以任何方式→(0,0) 都有1 ■ ◆ 例如: (xy)沿y→(0,0) ◆ 有z→1 y=kx 合
o x y 1 z = x 2 + y2 + 1 y =kx 在平面上的(0,0)点处 lim ( 1 ) 1 2 2 00 x y yx . (x,y ) ( 0 , 0 ) 以任何方式 例如: (x,y ) ( 0 , 0 ) 沿ykx z (和的极限等于极限的和 ) 1. 二重极限存在的例子 都有 z 1 有 z 1 有 故:在xoy平面上 点 .
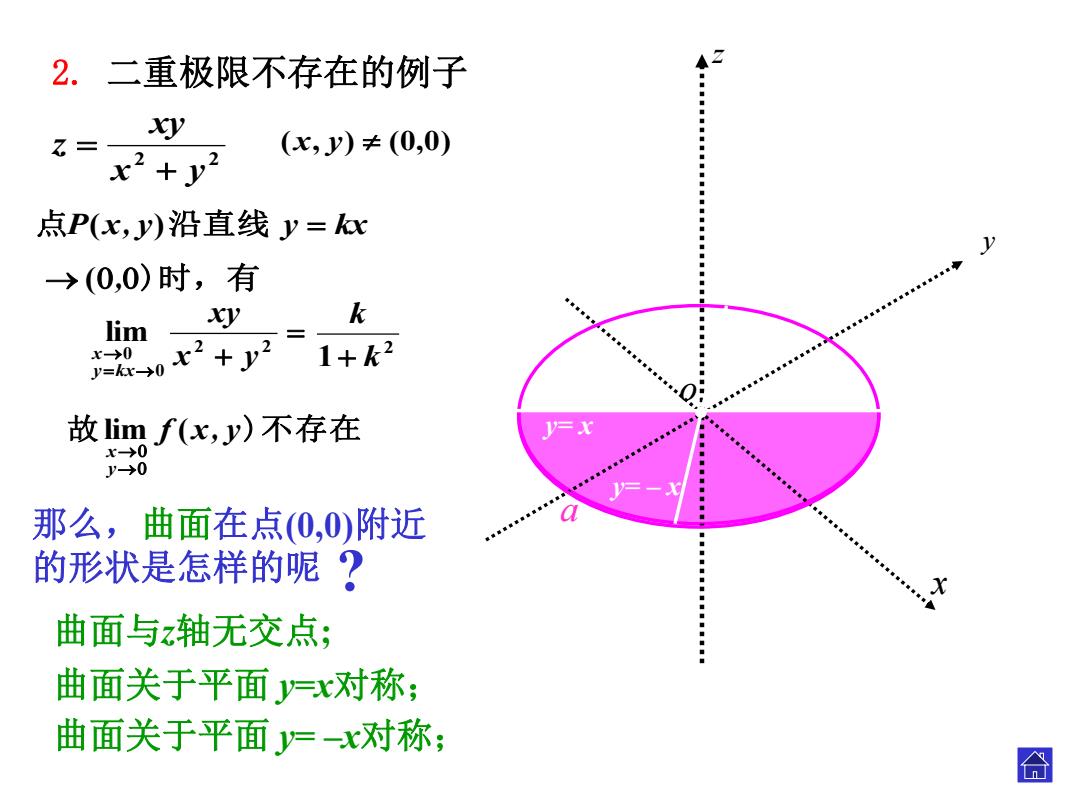
2.二重极限不存在的例子 y t= (x,y)≠(0,0) x2+y2 点P(x,y)沿直线y=x ◆ →(0,0)时,有 k lim y 00x2+y2 Jy=kx→0 1+k2 故imf(x,y)不存在 r-→0 y→0 那么,曲面在点0,0)附近 的形状是怎样的呢? · 比 曲面与z轴无交点; 曲面关于平面y=x对称; 曲面关于平面y=-x对称; 合
o x y 2 2 x y xy z 点P(x, y)沿直线 y kx 故 f x, y)不存在 y x lim ( 2 2 0 0 lim x y xy y kx x z a y= – x 2 1 k k (,)时,有 . . 那么,曲面在点(0,0)附近 的形状是怎样的呢 ? 曲面与z轴无交点; 曲面关于平面 y=x对称; 曲面关于平面 y= –x对称; y= x (x, y) (0,0) 2. 二重极限不存在的例子
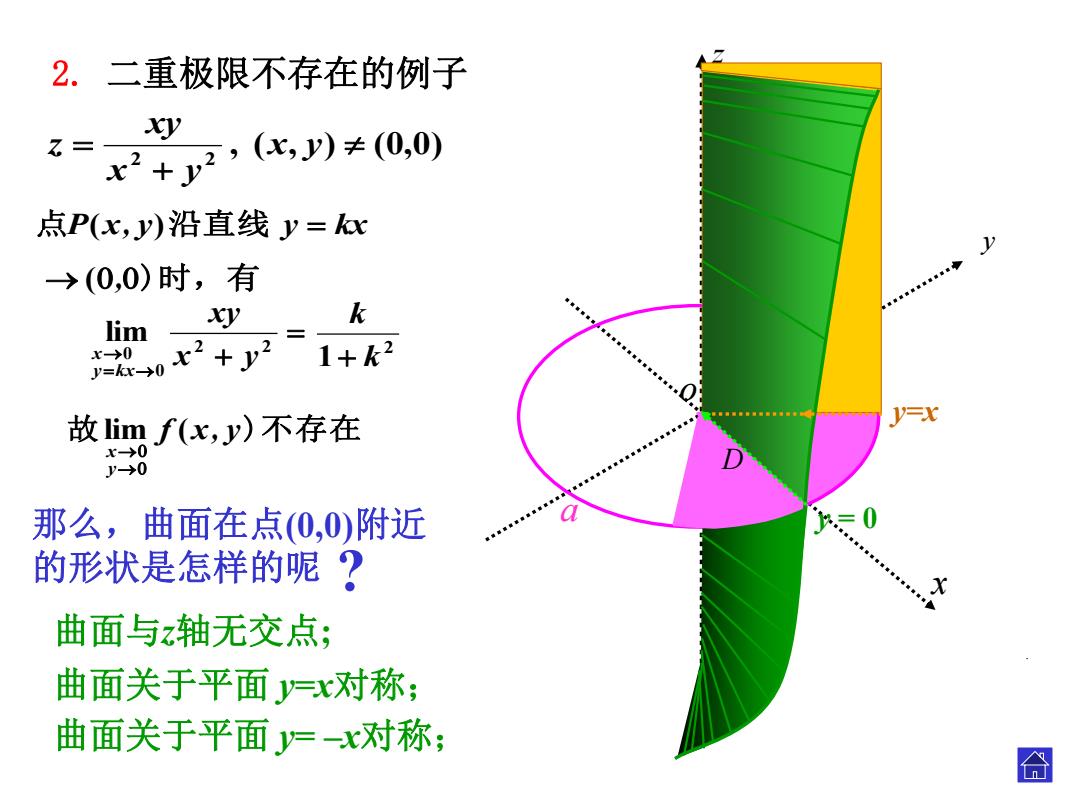
2.二重极限不存在的例子 x2+y2,(比,八≠(0,0) y 点P(x,y)沿直线y=x →(0,0)时,有 k lim Y 0x2+2 1+k2 V-X 故imf(x,y)不存在 r-→0 '→0 那么,曲面在点0,0)附近 的形状是怎样的呢? 曲面与z轴无交点; 曲面关于平面y=x对称; 曲面关于平面y=-x对称; 合
o x y , ( , ) (0,0) 2 2 x y x y xy z y=x z a . D . 那么,曲面在点(0,0)附近 的形状是怎样的呢 ? 曲面与z轴无交点; 曲面关于平面 y=x对称; 曲面关于平面 y= –x对称; y = 0 点P(x, y)沿直线 y kx 故 f x, y)不存在 y x lim ( 2 2 0 0 lim x y xy y kx x 2 1 k k (,)时,有 2. 二重极限不存在的例子
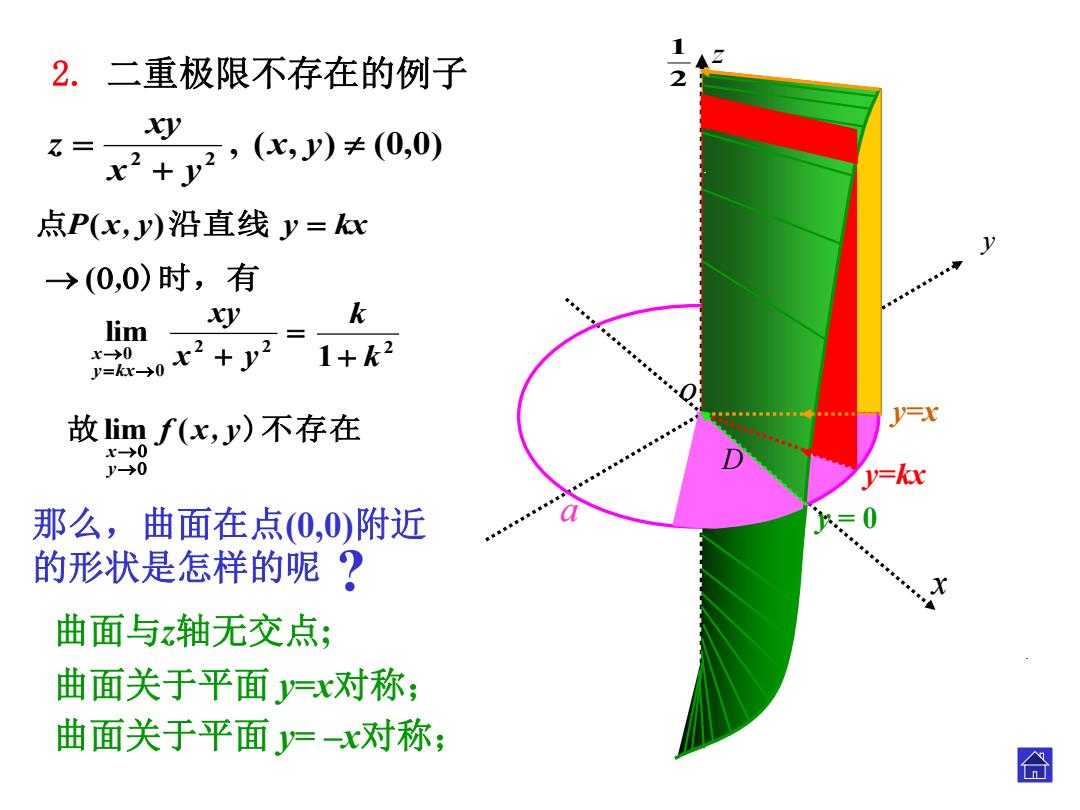
2.二重极限不存在的例子 2 t= x2+y2,(比,月≠(0,0) y 点P(x,y)沿直线y=x →(0,0)时,有 k lim y 0x2+2 1+k2 V=0 故imf(x,y)不存在 x→0 '→0 y=kx 那么,曲面在点0,0)附近 的形状是怎样的呢? 曲面与z轴无交点; 曲面关于平面y=x对称; 曲面关于平面y=-x对称; 合
o x y , ( , ) (0,0) 2 2 x y x y xy z y=kx y=x 2 1 z a . D . 那么,曲面在点(0,0)附近 的形状是怎样的呢 ? 曲面与z轴无交点; 曲面关于平面 y=x对称; 曲面关于平面 y= –x对称; y = 0 . 点P(x, y)沿直线 y kx 故 f x, y)不存在 y x lim ( 2 2 0 0 lim x y xy y kx x 2 1 k k (,)时,有 2. 二重极限不存在的例子

2.二重极限不存在的例子 1-2 t= x2+y2,(化月≠(0,0) y 1+k2 点P(x,y)沿直线y=x →(0,0)时,有 k lim y 02+2 1+k2 故imf(x,y)不存在 x→0 '→0 y=kx 那么,曲面在点0,0)附近 的形状是怎样的呢? 曲面与z轴无交点; 曲面关于平面y=x对称; 曲面关于平面y=-x对称; 合
o x y , ( , ) (0,0) 2 2 x y x y xy z y=kx y=x 2 1 k k 2 1 z a y= – x 2 1 . D . 那么,曲面在点(0,0)附近 的形状是怎样的呢 ? 曲面与z轴无交点; 曲面关于平面 y=x对称; 曲面关于平面 y= –x对称; . y = 0 . 点P(x, y)沿直线 y kx 故 f x, y)不存在 y x lim ( 2 2 0 0 lim x y xy y kx x 2 1 k k (,)时,有 2. 二重极限不存在的例子
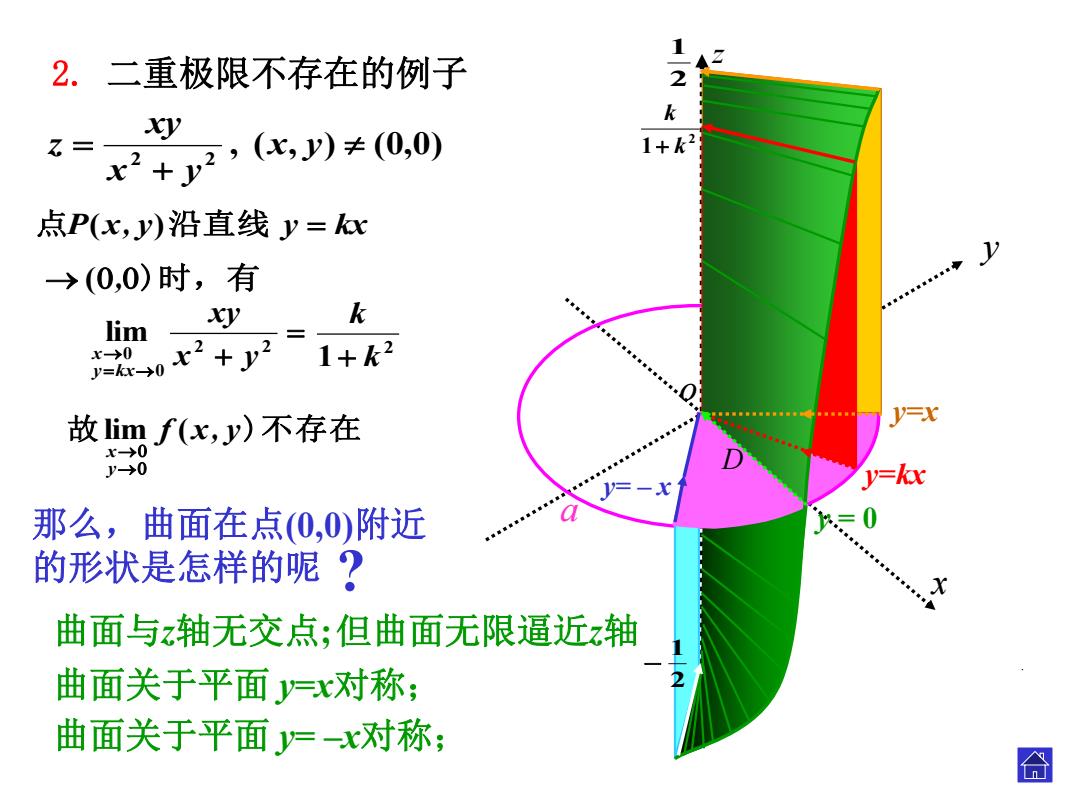
2.二重极限不存在的例子 1-2 t= x2+y2,(化)≠(0,0) y 1+k2 点P(x,y)沿直线y=x →(0,0)时,有 k lim y 02+2 1+k2 故imf(x,y)不存在 x→0 '→0 y=kx 那么,曲面在点0,0)附近 的形状是怎样的呢? 曲面与z轴无交点;但曲面无限逼近z轴 曲面关于平面y=x对称; 2 曲面关于平面y=-x对称; 合
o x y , ( , ) (0,0) 2 2 x y x y xy z y=kx y=x 2 1 k k 2 1 z a y= – x 2 1 . D . 那么,曲面在点(0,0)附近 的形状是怎样的呢 ? 曲面与z轴无交点; y = 0 曲面关于平面 y=x对称; 曲面关于平面 y= –x对称; . 但曲面无限逼近z轴 点P(x, y)沿直线 y kx 故 f x, y)不存在 y x lim ( 2 2 0 0 lim x y xy y kx x 2 1 k k (,)时,有 2. 二重极限不存在的例子
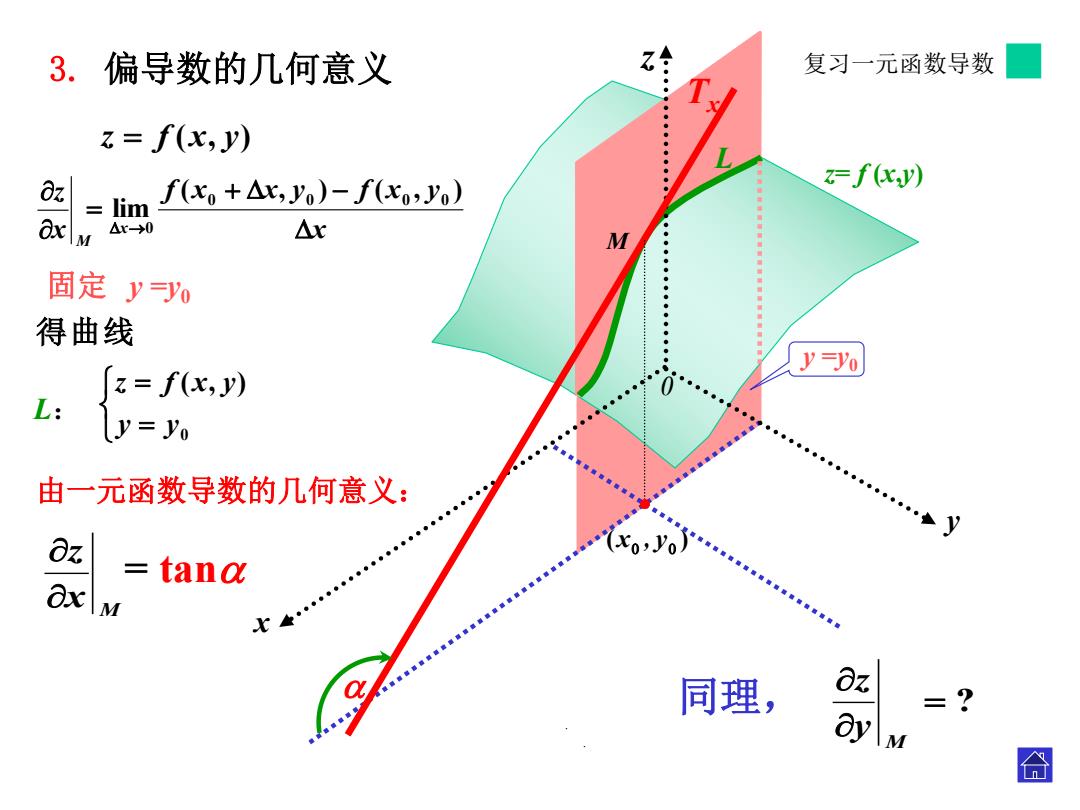
3.偏导数的几何意义 复习一元函数导数 ■ z=f(x,y) Oz z-f(xy) = fx+△x,yo)-f(xo,yo) lim ax △r→0 △x 固定yy 得曲线 y=o z=f(x,y) L: y=yo 由一元函数导数的几何意义: …◆y Ox tang Ox M … 同理, =? 合
x z y 0 z f (x, y) M x z x f x x y f x y x ( , ) ( , ) lim 0 0 0 0 0 x M z 由一元函数导数的几何意义: z= f (x,y) 0 ( , ) y y z f x y L: L 得曲线 = tan 3. 偏导数的几何意义 . y =y0 ( ) x , y ? M y z 同理, . M Tx 固定 y =y0 复习一元函数导数

3.偏导数的几何意义 z=f(x,y) Oz lim f(xo,Yo+Ay)-f(xo,Yo) -f(xy) Or 4y-→0 Ay 固定x=x0 …◆y x-x0 (xo;Jo 合
M z f (x, y) M y z y f x , y y f x , y y ( ) ( ) lim z= f (x,y) L ( ) x , y x =x0 固定 x =x0 Tx 3. 偏导数的几何意义 . x z y 0