
§7重积分的应用
§7 重积分的应用

主目 录(1-17)) 1求半径为R的球面与半顶角为α的内接锥面所围成的立体的体积。 2求抛物柱面z=4-x2,平面配x+y=4和三个坐标平面所围区域的体积 3求球面x2+y2+z2=a2与圆柱面x2+y2=ax(a>0)所围成的体积。 4 求圆柱面x2+y2=a2和x2+z2=a2所围立体的体积 5 求双曲抛物面2=y,圆柱面x2+y2=ax(a>0)与平面z=0所围成的体积。 6 旋转抛物面轉+y2=az(a>0)与圆锥面z=2a-√x2+y2所围体积. 7 求由旋转抛物面=Vy-,抛物柱面】V=x及平面y=1所围立体的体积 8 求椭圆抛物面3x2+y2=2,抛物柱面z=1-x2所围成的体积。 9 求球面x2+y2+z2=2az与球面x2+y2+z2=b2(a>b>0)所围成 的公共部分的体积 10曲面面积
4 2 4 . 2 求抛物柱面z x 2 ,平面 x y 和三个坐标平面所围区域的体积 1 求半径为R的球面与半顶角为 的内接锥面所围成的立体的体积。 . 4 求圆柱面x 2 y 2 a 2和x 2 z 2 a 2所围立体的体积 5 6 9 旋转抛物面轉 与圆锥面 所围体积. x y az (a ) z a x y 的公共部分的体积 求球面 x 2 y 2 z 2 2az 与球面 x 2 y 2 z 2 b 2 (a b 0)所围成 10 曲面面积 8 求椭圆抛物面3x 2 y 2 z, 抛物柱面 z 1 x 2 所围成的体积。 3 求球面x 2 y 2 z 2 a 2 与圆柱面 x 2 y 2 ax (a 0)所围成的体积。 求双曲抛物面 ,圆柱面x y ax a )与平面 z 0所围成的体积。 a xy z ( 0 2 2 主 目 录(1 – 17) 求由旋转抛物面x y z ,抛物柱面 y x及平面y 1 所围立体的体积. 2 2 1 7

11 锥面z=√x2+y2被圆柱面x2+y2=2x所割下部分的曲面面积 12 两相同正圆柱的轴互相直交,圆柱的底半径为,求一柱面被另一柱面 所割出部分的面积。■ 13 半球面z=√3a2-x2-y2与旋转抛物面x2+y2=2az所围成的全表 面积。 14 求圆柱面y2+z2=2z被圆锥面y2+z2=x2所截的有限部分的面积 15 求位于圆=2sin和圆=4sin0之间的均匀薄片的重心 16 求均匀半球体2:x2+y2+z2=a2,z≥01 的重心 17 求由抛物面z=1-x2-y2与平面z=0所围立体的重心
13 面积。 半球面 z 3a 2 x 2 y 2与旋转抛物面 x 2 y 2 2az 所围成的全表 14 2 求圆柱面 y 2 z 2 z被圆锥面 y 2 z 2 x 2所截的有限部分的面积 11 锥面z x 2 y 2被圆柱面 x 2 y 2 2x所割下部分的曲面面积 15 求位于圆r=2sin和圆r=4sin之间的均匀薄片的重心 17 求由抛物面z 1 x 2 y 2与平面 z 0 所围立体 的重心 求均匀半球体 Ω: x 2 y 2 z 2 a 2 ,z 0 的重心 所割出部分的面积。 12 两相同正圆柱的轴互相直交,圆柱的底半径为a,求一柱面被另一柱面 16

1.求半径为R的球面与半顶角为的内接锥面所围成的立体的体积 x2+y2+(z-R)2=R2$? 化为球系下的方程 VM∈Ω r-2R coso V:0≤r≤2Rc0S0 0≤0≤2m M 0≤p≤a R 2 P.=a y dosing dr(co
2 2 2 2 x y (z R) R R 化为球系下的方程 r=2R cos . V θ φ r φ r π α R φ d d sin d 2 cos 0 2 0 2 0 . R ( α ) π 3 4 1 cos 3 4 M V : 0 r 2Rcosφ 0 2 0 r z 0 x y M = 1.求半径为R的球面与半顶角为 的内接锥面所围成的立体的体积

2.求抛物柱面=4-x2,平面配x+y=4和三个坐标平面所围积。 v=JJJdxdydz 先选系 直角坐标 Ω Ω是曲顶柱体 上顶:z=4-x2 下底: z=0 Dg:x=0,y=0,2x+y=4 4 v-SSardrfdz -fdrf2(4-x")dy 40 3 合
Dxy: x = 0 , y = 0 , 2x + y = 4 。 。 2 z 0 V dxdydz 直角坐标 Dxy x V dxdy dz 。 x dx ( x )dy 3 40 4 0 y x Dxy 先选系 是曲顶柱体 求抛物柱面 平面 和三个坐标平面所围体积。 2. z x , x y 上顶: 下底: 2 z 4 x

2.求抛物柱面=4-x2,平面配x+y=4和三个坐标平面所围积。 1 4 Z=4-X2 2 合
2. 4 2 z x 求抛物柱面 平面 和三个坐标平面所围体积。 z x , x y . 0 z y x
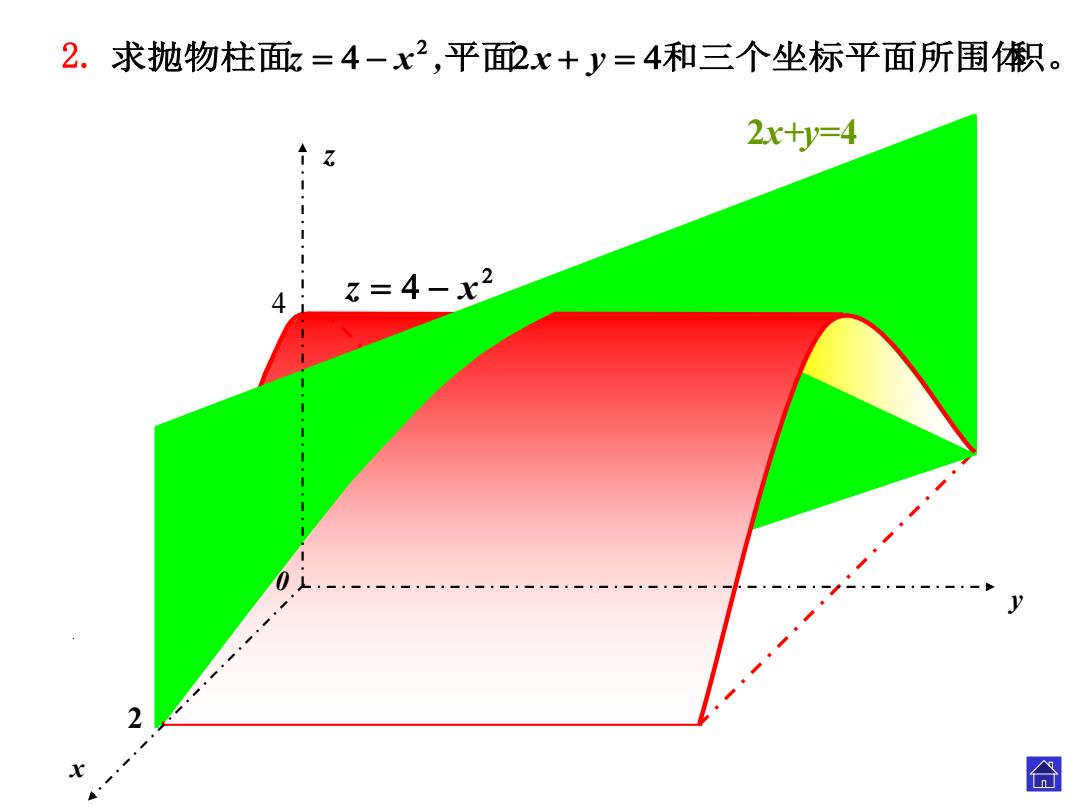
2.求抛物柱面=4-x2,平面配x+y=4和三个坐标平面所围积。 2x+y=4 4. 2=4-x2 2 合
2. 4 2 z x 2x+y= 4 求抛物柱面 平面 和三个坐标平面所围体积。 z x , x y . 0 z y x

2.求抛物柱面=4-x2,平面配x+y=4和三个坐标平面所围积。 41 Z=4-X2 合
2. x = 0 4 4 2 z x 求抛物柱面 平面 和三个坐标平面所围体积。 z x , x y . 0 z y x
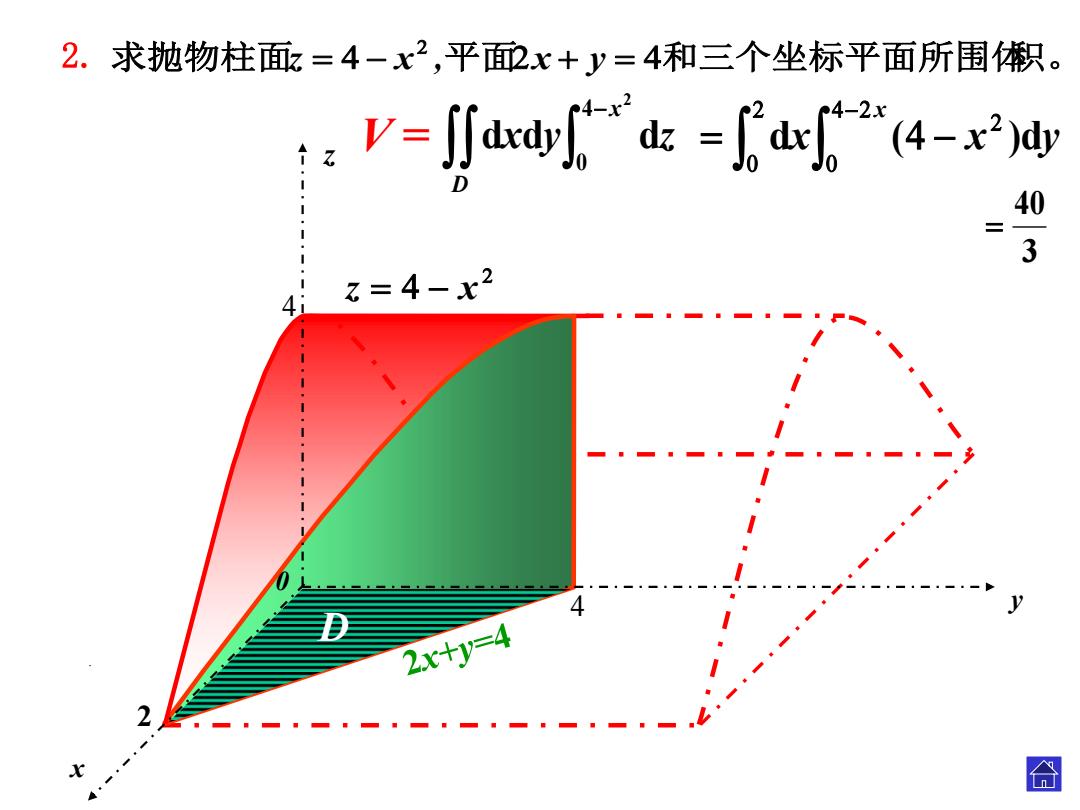
2.求抛物柱面?=4-x2,平面配x+y=4和三个坐标平面所围积。 zV=∬a=drg4- 40 3 41 2=4-x2 2x+y=4 合
2. z = 0 y = 0 z=0 y = 0 x = 0 4 4 2 2 40 d d d x D x y z . D x V = dx ( x ) dy 3 40 . . z x 求抛物柱面 平面 和三个坐标平面所围体积。 z x , x y . 0 z y x

3.求球面x2+y2+z2=a2与圆柱面x2+y2=c(a>0)所围成的体积 (指含在柱体内部分) 所围立体是曲顶柱体 上顶:z=V2-r2 先选系 柱面坐标 下底:z=-Va2-r2 Dy r =a cos0 0 a x 合
Dxy: a 2 2 z a r 柱面坐标 r =a cos 2 2 z a r r acos 。 所围立体是曲顶柱体 Dxy 0 y x (指含在柱体内部分) 求球面 与圆柱面 ) 所围成的体积 ( x y z a x y ax a 先选系 3. 上顶: 下底: