
第一章线性规划与单纯形法 ·§6线性规划应用举例 由于线性规划的理论与计算方法比较成熟,所以,对具体问题, 只要能建立起线性规划模型,计算是不成问题的,重要的是建立模 型。根据实际问题建立线性规划数学模型是本章的重点内容之一。 建立线性规划模型,一般要经过以下三个步骤: 1.设变量:每一个实际问题往往都归结为求一个最佳方案,为 了寻找最优方案,首先需要设定一组决策变量,用以表示待求方案。 2.列条件:每一个实际问题在解决时都要受到一定条件的制约, 因此,模型中要把各种制约因素用决策变量的线性等式或不等式表 示出来。 3.定目标:就是把所要达到的最优目标用决策变量的线性函数 求极值表示出来。 下面通过几个实例来说明建立线性规划模型的步骤和技巧
第一章 线性规划与单纯形法 •§6 线性规划应用举例 由于线性规划的理论与计算方法比较成熟,所以,对具体问题, 只要能建立起线性规划模型,计算是不成问题的,重要的是建立模 型。根据实际问题建立线性规划数学模型是本章的重点内容之一。 建立线性规划模型,一般要经过以下三个步骤: 1.设变量:每一个实际问题往往都归结为求一个最佳方案,为 了寻找最优方案,首先需要设定一组决策变量,用以表示待求方案。 2.列条件:每一个实际问题在解决时都要受到一定条件的制约, 因此,模型中要把各种制约因素用决策变量的线性等式或不等式表 示出来。 3.定目标:就是把所要达到的最优目标用决策变量的线性函数 求极值表示出来。 下面通过几个实例来说明建立线性规划模型的步骤和技巧

例10某工厂生产A、B两种产品,均需经过两道工序,每生产 一吨产品A需要经过第一道工序2小时,第二道工序3小时,每生 产一吨产品B需要经过第一道工序3小时,第二道工序4小时,可 供利用的第一道工序工时为12小时,第二道工序工时为24小时。 生产产品B的同时产出副产品C,每生产一吨产品B,可同时得 到2吨产品C而毋需外加任何费用。这副产品C一部分可以盈利,剩 下的只能报废。 出售产品A每吨能盈利400元、产品B每吨能盈利1000元,每销 售一吨副产品C能盈利300元,而剩余要报废的则每吨损失为200元。 经市场预测,在计划期内产品C最大销量为5吨。试列出本问题的线 性规划模型,决定A、B两种产品的产量,使工厂总的盈利为最大。 解:我们这样来设置决策变量: X1(吨)一产品A的产量; 2(吨)一产品B的产量: X3(吨)一产品C的销售量; X(吨)一产品C的报废量:
例10 某工厂生产A、B两种产品,均需经过两道工序,每生产 一吨产品A需要经过第一道工序2小时,第二道工序3小时,每生 产一吨产品B需要经过第一道工序3小时,第二道工序4小时,可 供利用的第一道工序工时为12小时,第二道工序工时为24小时。 生产产品B的同时产出副产品C,每生产一吨产品B,可同时得 到2吨产品C而毋需外加任何费用。这副产品C一部分可以盈利,剩 下的只能报废。 出售产品A每吨能盈利400元、产品B每吨能盈利1000元,每销 售一吨副产品C能盈利300元,而剩余要报废的则每吨损失为200元。 经市场预测,在计划期内产品C最大销量为5吨。试列出本问题的线 性规划模型,决定A、B两种产品的产量,使工厂总的盈利为最大。 解:我们这样来设置决策变量: x1(吨)—产品A的产量; x2(吨)—产品B的产量; x3(吨)—产品C的销售量; x4(吨)—产品C的报废量;
例11(下料问题)某厂接受了一批加工订货,须加工100套钢 架,每套由长2.9米、2.1米和1.5米的圆钢各一根组成。而现在仅有 一批7.4米的棒料毛坯,问应如何下料,可使所用的棒料根数最少? 解 本例的各种截料方案如下表所示: 下料 方案 根数 2 3 4 5 6 7 8 长度 2.9(米) 1 2 0 0 0 0 2.1(米) 0 2 2 3 1.5(米) 3 2 0 3 1 0 4 合计 7.47.3 7.2 7.16.6 6.5 6.3 6 料头 00.10.20.30.80.91.11.4 设按第种截料方案下料的棒料毛坯根数为X,=1,2,,8
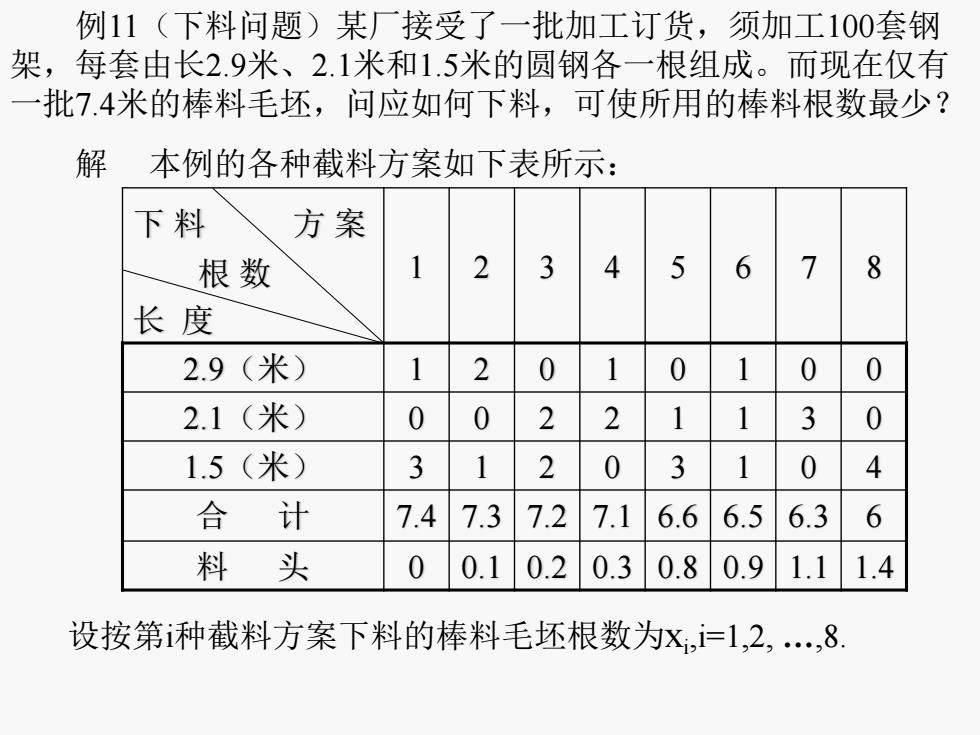
例11(下料问题)某厂接受了一批加工订货,须加工100套钢 架,每套由长2.9米、2.1米和1.5米的圆钢各一根组成。而现在仅有 一批7.4米的棒料毛坯,问应如何下料,可使所用的棒料根数最少? 解 本例的各种截料方案如下表所示: 下 料 方 案 根 数 长 度 1 2 3 4 5 6 7 8 2.9(米) 1 2 0 1 0 1 0 0 2.1(米) 0 0 2 2 1 1 3 0 1.5(米) 3 1 2 0 3 1 0 4 合 计 7.4 7.3 7.2 7.1 6.6 6.5 6.3 6 料 头 0 0.1 0.2 0.3 0.8 0.9 1.1 1.4 设按第i种截料方案下料的棒料毛坯根数为xi ,i=1,2, …,8
例12根据四种食物所含维生素A、B、C的成分及食物的市场 价格调查,按照医生提出的对每个人每天所需的营养要求,可得下 面的表格: (表中营养含量为每公斤含量) 营养 食物种类 含量 甲 乙 丙 丁 最 低 营养成分 要量 维生素A(国际单位) 1000 1500 1750 3250 4000 维生素B (毫克) 0.6 0.27 0.68 0.3 维生素C (毫克) 17.5 7.5 0 30 30 单 价 (元/kg) 0.8 0.5 0.9 1.5 问怎样采购食物才能在保证营养要求的前提下花费最省? 解:设每天采购甲、乙、丙、丁四种食物分别为x1,X2,X3,飞4(kg)
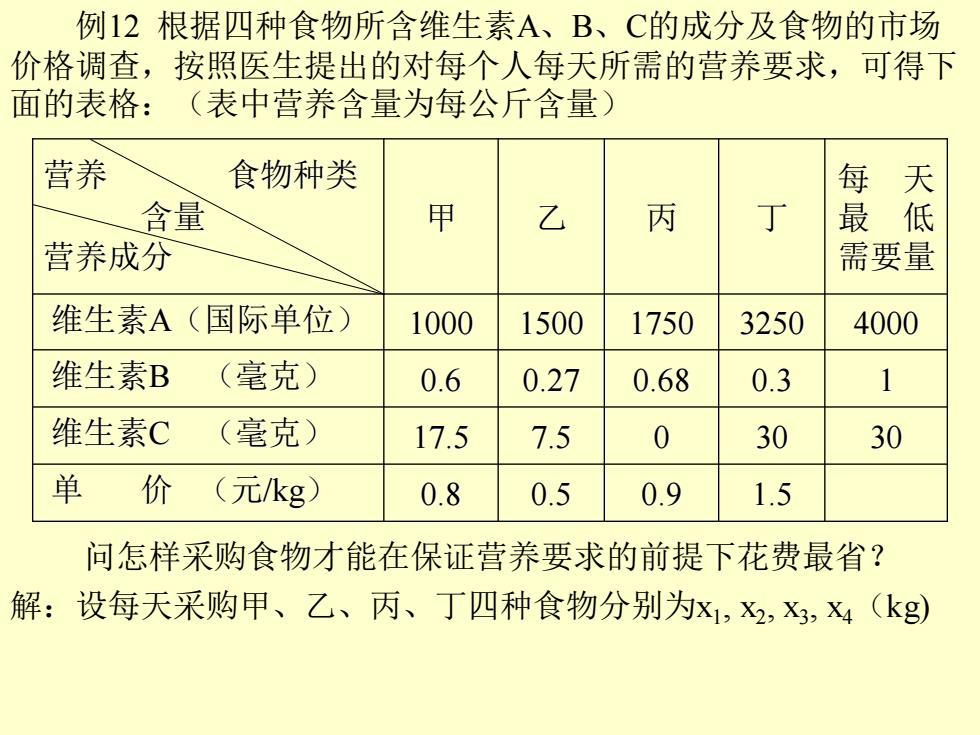
例12 根据四种食物所含维生素A、B、C的成分及食物的市场 价格调查,按照医生提出的对每个人每天所需的营养要求,可得下 面的表格:(表中营养含量为每公斤含量) 营养 食物种类 含量 营养成分 甲 乙 丙 丁 每 天 最 低 需要量 维生素A(国际单位) 1000 1500 1750 3250 4000 维生素B (毫克) 0.6 0.27 0.68 0.3 1 维生素C (毫克) 17.5 7.5 0 30 30 单 价 (元/kg) 0.8 0.5 0.9 1.5 问怎样采购食物才能在保证营养要求的前提下花费最省? 解:设每天采购甲、乙、丙、丁四种食物分别为x1 , x2 , x3 , x4(kg)

例13(投资问题)某部门在今后五年内考虑给下列颜目投资, 已知:项目A,从第一年到第四年初需要投资,并于次年泰回收本 利115%;项目B,第三年初需要投资,到第五年末能@梦利125% 但规定最大投资额不超过4万元:项目C,第二年初需要资,到第 五年末能回收本利140%,但规定最大投资额不超过3就;顶 五年内每年初都可投资,于当年末归还,并加利息6%翻 该部门现有资金10万元,问应如何确定这些项目的投资,衡到 第五年末拥有资金本利总额最大? 解 这是个连续投资问题,按投资的时间要求,设各年初投 资额如亦表所示: 年份 二三 四五 X X3 X6 Xo X1 X X X5 X8 X10X11
例13 (投资问题) 某部门在今后五年内考虑给下列项目投资, 已知:项目A,从第一年到第四年初需要投资,并于次年末回收本 利115%;项目B,第三年初需要投资,到第五年末能回收本利125%, 但规定最大投资额不超过4万元;项目C,第二年初需要投资,到第 五年末能回收本利140%,但规定最大投资额不超过3万元;项目D, 五年内每年初都可投资,于当年末归还,并加利息6%. 该部门现有资金10万元,问应如何确定这些项目的投资,使到 第五年末拥有资金本利总额最大? 解: 这是个连续投资问题,按投资的时间要求,设各年初投 资额如下表所示: 项目 年份 一 二 三 四 五 A x1 x3 x6 x9 B x7 C x4 D x2 x5 x8 x10 x11
例14某工厂有三个车间生产同一种产品。每件产铺4个零件 1和3个零件2组成。这两种零件需耗用两种原材料。已两种原 材料的供应量分别为300kg和500kg。由于三个车间拥有被备及工 艺条件不同,每个工班原材料耗用量和零件产量也同具体如不 表所示。 问三个车间应各开多少工班,才能使该产配套数达 最大2 项目 每班用料数(kg) 每班产量(件数 车间 A材料 B材料 零件1 零件2 车间 8 6 7 二车间 5 9 6 9 三车间 3 8 8 4 解设x1,x2,X分别为一、二、三叁个车间所开工班数,则 这三个森间所生产的零件1总数为7x+6x+8x,零件2总数为 5付9志 要注意的是,本例的目的不是生产各种零件的总数最 是要筋品的配套数最大。因此,目标函数应为 mamn距0x,+6x,+8x)/4,(5x+9x,+4x)/3] 这个目数不是线性函数,可以通过恰当的变换将其变为线性函 数:令y +6x+8x3)/4,(5x1+9x2+4x3)/3]
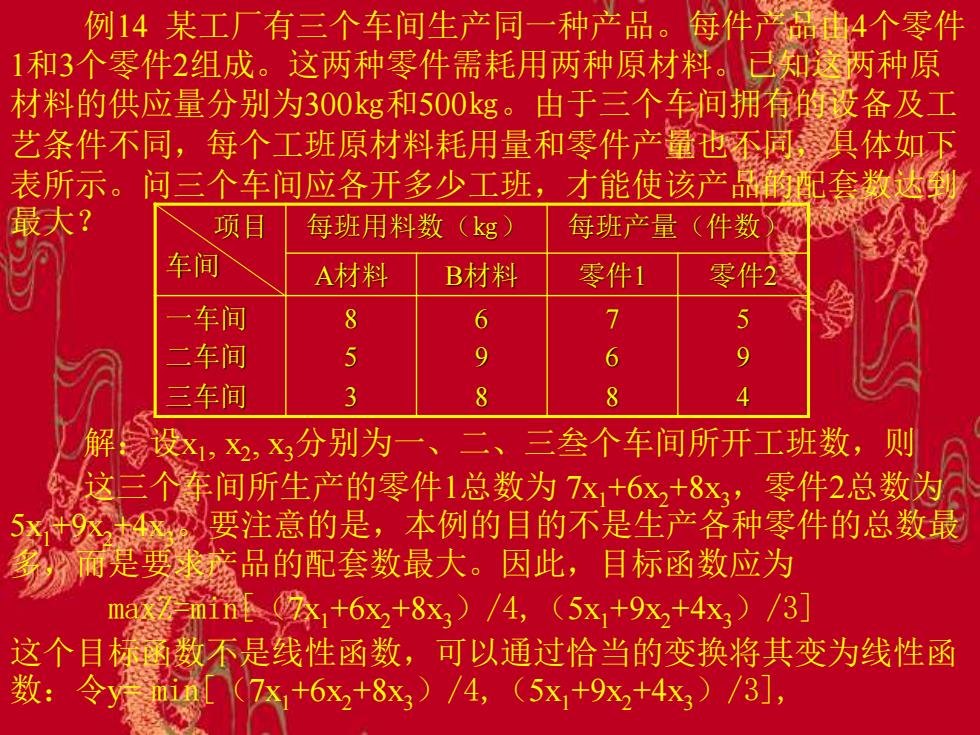
例14 某工厂有三个车间生产同一种产品。每件产品由4个零件 1和3个零件2组成。这两种零件需耗用两种原材料。已知这两种原 材料的供应量分别为300㎏和500㎏。由于三个车间拥有的设备及工 艺条件不同,每个工班原材料耗用量和零件产量也不同,具体如下 表所示。问三个车间应各开多少工班,才能使该产品的配套数达到 最大? 项目 车间 每班用料数(㎏) 每班产量(件数) A材料 B材料 零件1 零件2 一车间 二车间 三车间 8 5 3 6 9 8 7 6 8 5 9 4 解:设x1 , x2 , x3分别为一、二、三叁个车间所开工班数,则 这三个车间所生产的零件1总数为 7x1+6x2+8x3,零件2总数为 5x1+9x2+4x3。要注意的是,本例的目的不是生产各种零件的总数最 多,而是要求产品的配套数最大。因此,目标函数应为 maxZ=min[(7x1+6x2+8x3)/4,(5x1+9x2+4x3)/3] 这个目标函数不是线性函数,可以通过恰当的变换将其变为线性函 数:令y= min[(7x1+6x2+8x3)/4,(5x1+9x2+4x3)/3]

令y=min[(7x1+6x2+8x3)/4,(5x+9x2+4x) 则此式与下面两个不等式等价: (7x,+6x+8x)/42y,(5x+9x2+4x)/32 于是,本例的线性规划模型可以列出为: maxZ-y 7x1+6X2+8x3-4y20 5x1+9x2+4x33y20 8x1+5x2+3x≤300 6x1+9x2+8x,≤500 X1X2,X3y20
令y= min[(7x1+6x2+8x3)/4,(5x1+9x2+4x3)/3] 则此式与下面两个不等式等价: (7x1+6x2+8x3)/4≥y, (5x1+9x2+4x3)/3 ≥y 于是,本例的线性规划模型可以列出为: maxZ=y 7x1+6x2+8x3 -4y≥0 5x1+9x2+4x3 -3y≥0 8x1+5x2+3x3 ≤300 6x1+9x2+8x3 ≤500 x1 ,x2 ,x3 ,y≥0

本章作业 。 P26:4(1):5(1) 。P27:8 P29:11
本 章 作 业 • P26: 4(1);5(1) • P27: 8 • P29: 11