
® §十整数规划问题 在前面的线性规划问题中,它的解都假设为可以取连续数值。 但是在许多实际问题中,决策变量仅仅取整数值时才有意义,比如 变量表示的是工人的人数、机器的台数、货物的箱数、装货的车皮 数等等。为了满足整数解的要求,比较自然的简便方法似乎就是把 用线性规划方法所求得的非整数解进行“四舍五入”取整或“舍尾 取整”处理。当然,这样做有时确实也是有效的,可以取得与整数 最优解相近的可行整数解,因此它是实际工作中经常采用的方法。 但是实际问题中并不都是如此,有时这样处理得到的解可能不是原 问题的可行解,有的虽是原问题的可行解,但却不是整数最优解。 (详见后面例1)。因而有必要专门研究只取整数解的线性规划的 解法问题。 在一个线性规划问题中,如果它的所有决策变量都要求取整数 时,就称为纯整数规划;如果仅部分决策变量要求取整数则称为混 合整数规划,二者统称为整数规划。整数规划的一个特殊情形是01 规划,它的决策变量取值仅限于0或两个逻辑值。整数规划是近几 年发展起来的规划论的一个分支
§1 整数规划问题 在前面的线性规划问题中,它的解都假设为可以取连续数值。 但是在许多实际问题中,决策变量仅仅取整数值时才有意义,比如 变量表示的是工人的人数、机器的台数、货物的箱数、装货的车皮 数等等。为了满足整数解的要求,比较自然的简便方法似乎就是把 用线性规划方法所求得的非整数解进行“四舍五入”取整或“舍尾 取整”处理。当然,这样做有时确实也是有效的,可以取得与整数 最优解相近的可行整数解,因此它是实际工作中经常采用的方法。 但是实际问题中并不都是如此,有时这样处理得到的解可能不是原 问题的可行解,有的虽是原问题的可行解,但却不是整数最优解。 (详见后面例1)。因而有必要专门研究只取整数解的线性规划的 解法问题。 在一个线性规划问题中,如果它的所有决策变量都要求取整数 时,就称为纯整数规划;如果仅部分决策变量要求取整数则称为混 合整数规划,二者统称为整数规划。整数规划的一个特殊情形是0-1 规划,它的决策变量取值仅限于0或1两个逻辑值。整数规划是近几 年发展起来的规划论的一个分支

下面我们举例说明对于整数规划问题,用“四舍五入”取 整,或“舍尾取整”方法,是行不通的。 例1现有甲、乙两种货物拟用集装箱托运,每件货物的体 积、重量、可获利润,以及集装箱的托运限制如下表: 货物 体积(米3件) 重量(万斤件利润(万元/件) 甲 5 2 20 乙 4 5 10 托运限制 24 13 试确定集装箱中托运甲、乙货物的件数,使托运利润最大。 设x,x分别表示甲、乙货物托运的件数(整数),则该问题的 数学模型为: maxZ=20x+10x2 (1) 5x+4x2≤24 (2) 2x1+5x2≤13 (3) X1X2≥0,整数 (4)
下面我们举例说明对于整数规划问题,用“四舍五入”取 整,或“舍尾取整”方法,是行不通的。 例1 现有甲、乙两种货物拟用集装箱托运,每件货物的体 积、重量、可获利润,以及集装箱的托运限制如下表: 货物 体积(米3 /件) 重量(万斤/件)利润(万元/件) 甲 乙 5 4 2 5 20 10 托运限制 24 13 试确定集装箱中托运甲、乙货物的件数,使托运利润最大。 设x1 ,x2分别表示甲、乙货物托运的件数(整数),则该问题的 数学模型为: maxZ=20x1+10x2 ⑴ 5x1+4x2 ≤24 ⑵ 2x1+5x2 ≤13 ⑶ x1 ,x2 ≥0,整数 ⑷

这里货物的件数只能是整数,所以这是一个纯整数规划。荐先不考 虑整数限⑧永得问题的最优解为: x1=4.8,x2=0,maxZ=96 由于X二4:8不符合整数要求,所以该解不是整数规划的最优解。 是否可以将非整数解用“四舍五入”方法处理呢?事实上,如 果将x=4.8,x2=0近似为x=5,X2=0,则该解不符合体积限制条件(2): 5x1+4X≤24 因而它不是最优解; 那么用“舍尾取整”方法处理又如何呢?将x=4.8,x2=0“舍 尾取整”为x=4,X,0,显然满足各约束条件,因而它是整数规划 问题的可行解,但它不是整数最优解。因为它对应的目标函数值 Z=80,而x=4,x2=1这个解亦是可行解,但它对应的目标函数值 Z=90。 个 由此例看出,简单的处理方法常常得不到整数规划的最优解, 甚至得不到可行解。 如何求得这类问题的整数最优解呢?到目前为止,整数规划还 没有一种很满意的和有效的解法。现在用以求解整数规划的方法基 本都是将整数规划变为一系列线性规划来求解的。我们将介绍两种
这里货物的件数只能是整数,所以这是一个纯整数规划。若先不考 虑整数限制,可求得问题的最优解为: x1=4.8,x2=0, maxZ=96 由于x1=4.8不符合整数要求,所以该解不是整数规划的最优解。 是否可以将非整数解用“四舍五入”方法处理呢?事实上,如 果将x1=4.8,x2=0近似为x1=5,x2=0,则该解不符合体积限制条件⑵: 5x1+4x2 ≤24 因而它不是最优解; 那么用“舍尾取整”方法处理又如何呢?将x1=4.8,x2=0 “舍 尾取整”为x1=4,x2=0,显然满足各约束条件,因而它是整数规划 问题的可行解,但它不是整数最优解。因为它对应的目标函数值 Z=80,而x1=4,x2=1这个解亦是可行解,但它对应的目标函数值 Z=90。 由此例看出,简单的处理方法常常得不到整数规划的最优解, 甚至得不到可行解。 如何求得这类问题的整数最优解呢?到目前为止,整数规划还 没有一种很满意的和有效的解法。现在用以求解整数规划的方法基 本都是将整数规划变为一系列线性规划来求解的。我们将介绍两种 方法——分枝定界法和割平面法

®§2分枝定界法 分枝定界法是求解整数规划的常用算法,既可用来解全部变量 取值都要求为整数的纯整数规划,又可用以求解混合整数规划 该算法的基本思路是:先不考虑整数限制,求出相应的线性规 划的最优解,若此解不符合整数要求,则去掉不包含整数解的部分 可行域,将可行域D分成D1、D2两部分(分枝),然后分别求解这 两部分可行域对应的线性规划,如果它们的解仍不是整数解,则继 续去掉不包含整数解的部分可行域,将可行域D1或D2分成D3与D4两 部分,再求解D,与D4对应的线性规划,.,在计算中若已得到一 个整数可行解X,则以该解的目标函数值乙作为分枝的界限,如果 某线性规划的目标值Z≤Z。,就没有必要继续分枝,因为分枝 (增加约束)的结果所得的最优解只能比乙,更差。反之若乙>Z, 则该线性规划分枝后,有可能产生比乙,更好的整数解,一旦真的产 生了一个更好的整数解,则以这个更好的整数解目标值作为新的界 限,六继续进行分枝,直至产生不出更好的整数解为止。 下面以实例来说明算法的步骤
§2 分枝定界法 分枝定界法是求解整数规划的常用算法,既可用来解全部变量 取值都要求为整数的纯整数规划,又可用以求解混合整数规划。 该算法的基本思路是:先不考虑整数限制,求出相应的线性规 划的最优解,若此解不符合整数要求,则去掉不包含整数解的部分 可行域,将可行域D分成D1、D2两部分(分枝) ,然后分别求解这 两部分可行域对应的线性规划,如果它们的解仍不是整数解,则继 续去掉不包含整数解的部分可行域,将可行域D1或D2分成D3与D4两 部分,再求解D3与D4对应的线性规划,……,在计算中若已得到一 个整数可行解X 0 ,则以该解的目标函数值Z0作为分枝的界限,如果 某一线性规划的目标值Z≤ Z0 ,就没有必要继续分枝,因为分枝 (增加约束)的结果所得的最优解只能比Z0 更差。反之若Z> Z0 , 则该线性规划分枝后,有可能产生比Z0 更好的整数解,一旦真的产 生了一个更好的整数解,则以这个更好的整数解目标值作为新的界 限,继续进行分枝,直至产生不出更好的整数解为止。 下面以实例来说明算法的步骤

例2求解下面整数规划 maxZ=40x+90x2 1) 8 9x1+7X2=56 9x+7x≤56 (2) Z=40x+90x2 7x+20x2≤70 (3) X1,X2≥0 (4) X1,X2整数 7x1+20x2=70 (5) 解:先不考虑条件(⑤),求解相 10 X 应的线性规划问题L,得最优解 x=4.81,X2=1.82,Z0=356 (见图) 求解线性规划L1、L2 该解不是整数解。选择其中一个 得最优解为: 非整数变量,如x=4.81,对问题 问题L1: 问题L2: L分别增加约束条件: L+X1≤4 L+X1≥5 X1≤4,X1≥5 x1=4.00 X=5.00 将问题L分解为两个子问题L,L? (分枝),也就是去掉问题L不含 x2=2.10 x2=1.57 整数解的一部分可行域,将原可 Z=349 Z2=341 行域D变为D1、D2两部分(如图)
例2 求解下面整数规划 maxZ=40x1+90x2 ⑴ 9x1+ 7x2 ≤56 ⑵ 7x1 +20x2 ≤70 ⑶ x1 ,x2 ≥0 ⑷ x1 ,x2 整数 ⑸ 解:先不考虑条件⑸,求解相 应的线性规划问题L,得最优解 x1=4.81,x2=1.82,Z0=356(见图) x2 8 0 6 4 10 x1 9x1+ 7x2=56 7x1+20x2=70 Z=40x1+90x2 该解不是整数解。选择其中一个 非整数变量,如x1=4.81,对问题 L分别增加约束条件: x1≤4,x1≥5 将问题L分解为两个子问题L1,L2 (分枝),也就是去掉问题L不含 整数解的一部分可行域,将原可 行域D变为D1、D2两部分(如图)。 4 D1 D2 求解线性规划L1、L2 得最优解为: 问题L1: L+ x1≤4 问题L2: L+ x1≥5 x1=4.00 x2=2.10 Z1=349 x1=5.00 x2=1.57 Z2=341

+本因为没有得到整数解,所继续对进行分解,增加约束: X2≤2,X2≥3 将分解成问题L与L4,并求得最优解如下: 问题L3:L1+X≤2 问题L4:L1+X,≥3 x1=4.00,X2=2.00 x1=1.42,x2=3.00 Z3=340 Z4=327 问题L3的解已是整数解,它的目标值乙=340,大于问题L4的目标值, 所以问题L4己无必要再分枝。但由于问题L2的目标值Z2大于Z3,分解 2还有可能产生更好的整数解,因此继续对L,分枝。增加约束 A x≤1,x≥2 将L2分解成问题L与L6,并求解,结果如下: 问题L5:L2+x2≤1 问题L6:L2+x2≥2 x1=5.44,x2=1.00 无可行解 Z5=308 问题L5的Z=308<Z,=340,所以不必分解了;问题L6无可行解, 于是可以断定问题L3的解:x,=4.00,x,=2.00即为最优整数解
因为没有得到整数解,所以继续对L1进行分解,增加约束: x2≤2,x2≥3 将L1分解成问题L3与L4,并求得最优解如下: 问题L3: L1+ x2≤2 问题L4:L1+x2≥3 x1 =4.00,x2 =2.00 Z3=340 x1=1.42,x2=3.00 Z4=327 问题L3的解已是整数解,它的目标值Z3=340,大于问题L4的目标值, 所以问题L4已无必要再分枝。但由于问题L2的目标值Z2大于Z3,分解 L2还有可能产生更好的整数解,因此继续对L2分枝。增加约束 x2≤1,x2≥2 将L2分解成问题L5与L6,并求解,结果如下: 问题L5: L2+ x2≤1 问题L6:L2+x2≥2 x1=5.44,x2=1.00 Z5=308 无可行解 问题L5的Z5 =308< Z3=340 ,所以不必分解了;问题L6无可行解, 于是可以断定问题L3的解: x1 =4.00,x2 =2.00即为最优整数解
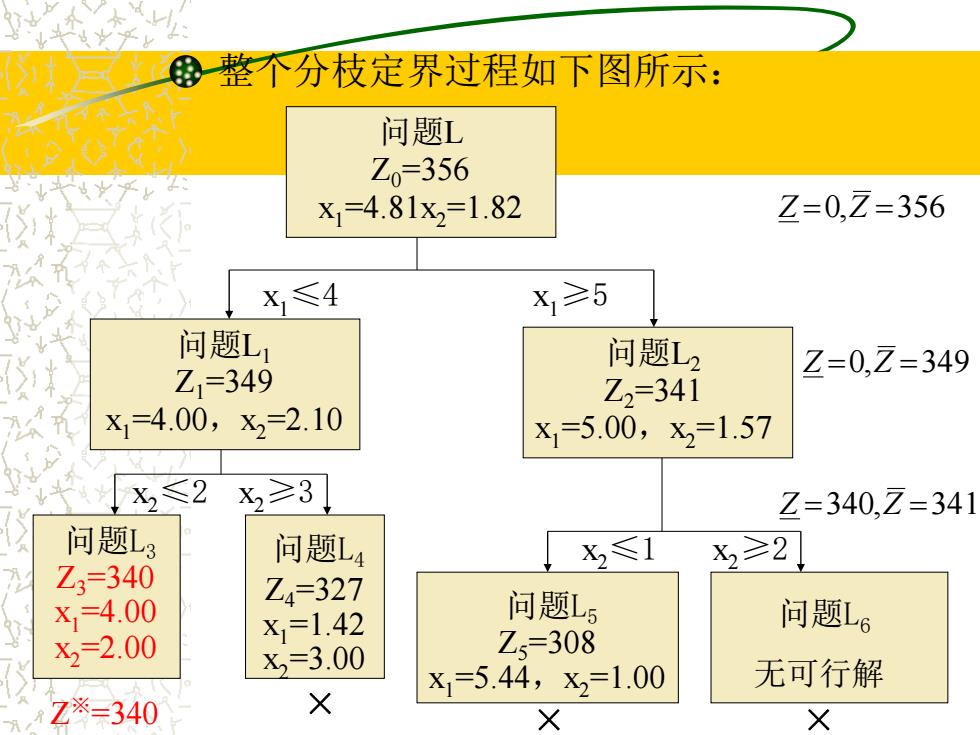
整个分枝定界过程如下图所示: 问题 Z0=356 x1=4.81x2=1.82 Z=0,Z=356 X,≤4 x1≥5 问题L 问题L2 Z1=349 Z=0,Z=349 Z2=341 x1=4.00,x2-2.10 x1=5.00,x2=1.57 1x2≤2 X2≥3 Z=340,Z=341 问题L3 问题L4 x2≤1 X2≥2 Z3=340 X,-4.00 Z4=327 x=1.42 问题L5 问题L6 x2=2.00 x=3.00 Z,=308 x1=5.44,x2=1.00 无可行解 Z※=340 × X X
整个分枝定界过程如下图所示: Z =0,Z =356 问题L Z0=356 x1=4.81x2=1.82 问题L1 Z1=349 x1=4.00,x2=2.10 问题L2 Z2=341 x1=5.00,x2=1.57 问题L3 Z3=340 x1=4.00 x2=2.00 问题L4 Z4=327 x1=1.42 x2=3.00 问题L5 Z5=308 x1=5.44,x2=1.00 问题L6 无可行解 Z =0,Z =349 Z =340,Z =341 x1≤4 x1≥5 x2≤2 x2≥3 x2≤1 x2≥2 Z × × × ※=340

用分枝定界法求解整数规划的步骤可总结如下: 步骤求解与整数规划相对应的线性规划L,若L无可行解, 则整数规划也没有可行解,计算停;若L的最优解是整数解,则该 解即为整数规划的最优解,计算停;若L的最优解不是整数解,则 转步骤2。 步骤2(分枝)在L的最优解中任选一个不符合整数条件的变量 XB,其值为(Bb),[(Bb)]为小于(B-b),的最大整数,构造两 个约束条件XB1≤[(Bb)]和X≥[(Bb)]+1 将这两个约束条件分别加在问题L的约束条件上,形成两个子问题 L1和L2,并求解L和L2。 步骤3(定界)取整数解中最大目标值为界限值Z(下界),如果 计算中尚无整数解,则取Z=-∞。检查分枝L,若它的最优解不是 整数解,且Z>Z,则重复步骤2,若Z≤Z,则L不再分枝。 重复步骤2、步骤3,直至所有分枝都不能再分解为止,这时界 限值Z对应的整数解即为原问题的最优解。 用分枝定界法可解纯整数规划问题和混合整数规划问题。它比 穷举法优越,因为它仅在一部分可行的整数解中寻求最优解,计算 量比穷举法小。若变量数目很大,其计算工作量也是相当可观的
用分枝定界法求解整数规划的步骤可总结如下: 步骤1:求解与整数规划相对应的线性规划L,若L无可行解, 则整数规划也没有可行解,计算停;若L的最优解是整数解,则该 解即为整数规划的最优解,计算停;若L的最优解不是整数解,则 转步骤2。 步骤2(分枝)在L的最优解中任选一个不符合整数条件的变量 XBi,其值为(B-1b)i,[(B-1b)i ]为小于(B-1b)i的最大整数,构造两 个约束条件 XBi ≤ [(B-1b)i ]和XBi≥ [(B-1b)i ] +1 将这两个约束条件分别加在问题L的约束条件上,形成两个子问题 L1和L2,并求解L1和L2 。 步骤3(定界 )取整数解中最大目标值为界限值Z(下界),如果 计算中尚无整数解,则取Z=-∞。检查分枝Li,若它的最优解不是 整数解,且Zi>Z,则重复步骤2,若Zi≤Z,则Li不再分枝。 重复步骤2、步骤3,直至所有分枝都不能再分解为止,这时界 限值Z对应的整数解即为原问题的最优解。 用分枝定界法可解纯整数规划问题和混合整数规划问题。它比 穷举法优越,因为它仅在一部分可行的整数解中寻求最优解,计算 量比穷举法小。若变量数目很大,其计算工作量也是相当可观的