
§5最小费用最大流 在实际网络问题中,不仅要考虑从v到v,的流量最大,而且还 要考虑可行流在网络传送过程中的费用问题,这就是网络的最小费 用、最大流问题。 最小费用最大流问题的一般提法:已知容量网络D=(V,A,①) 每条弧(,V)除了已给出容量c:外,还给出了单位流量的传输费 用b≥0,记作D=(V,A,C,B),其中b∈B。要在费用、容量 网络D中寻找V,→,的最大流f={f},且使流的总传输费用: b(f)=∑bf最小。 从上一讲可知,最大流的求法就是在容量网络上从某个可行流 出发,设法找到一条从,→?,的增广链,然后沿着此增广链调整流 量,作出新的流量增大了的可行流。在这个新的可行流基础再 找它的增广链。如此反复进行,直至再找不出增广链时,就得到了 该网络的最大流。 现在要寻求最小费用的最大流,我们首先考察一下,当沿着 条关于可行流f的增广链,以01调整f得到新的可行流f时
§5 最小费用最大流 ❖ 在实际网络问题中,不仅要考虑从vs 到vt 的流量最大,而且还 要考虑可行流在网络传送过程中的费用问题,这就是网络的最小费 用、最大流问题。 ❖最小费用最大流问题的一般提法:已知容量网络D=(V,A,C), 每条弧(vi ,vj)除了已给出容量cij 外,还给出了单位流量的传输费 用bij ≥0,记作D=(V,A,C,B),其中 bij ∈B。要在费用、容量 网络D中寻找 vs →vt 的最大流 f ={f ij},且使流的总传输费用: b(f )= ∑bij f ij 最小。 ❖ 从上一讲可知,最大流的求法就是在容量网络上从某个可行流 出发,设法找到一条从vs →vt 的增广链,然后沿着此增广链调整流 量,作出新的流量增大了的可行流。在这个新的可行流基础上再寻 找它的增广链。如此反复进行,直至再找不出增广链时,就得到了 该网络的最大流。 ❖ 现在要寻求最小费用的最大流,我们首先考察一下,当沿着一 条关于可行流 f 的增广链μ,以θ=1调整 f 得到新的可行流 f′时

总费用b(f)比b(f)增加多少? .在前向弧上f=+1,在后向弧上f后1, bW)bW)=∑b0f)+∑b,ff)] ->bi >bu 即沿着关于可行流∫的增广链,增加一个单位运量时,所增加的总 费用是上所有前向弧的费用之和减去所有后向弧的费用和。 我们称此费用为该增广链的费用。 可以证明:若f是流量为()的所有可行流中费用最小者/而u 是关于f的所有增广链中费用最小的增广链,那么沿着法调整f, 得到的可行流f'就是流量为f)的所有可行流中的最小费用流。这 样,当f'是最大流时,它就是我们所要求的最小费用最木流。 上述命题为我们提供了寻找最小费用最大流的思路:先我个 最小费用可行流,再找出关于该可行流的最小费用增广链,沿此链 调整流量,则得到一个新的流量增大了的最小费用流,然后对新的 最小费用流重复上述方法,一直调整到网络的最大流出现为止,使 得到了所考虑网络的最小费用最大流
总费用b(f′)比b(f )增加多少? ∵在前向弧μ+上 f ij′= f ij+1,在后向弧μ -上 f ij′= f ij-1, ∴ b(f′)-b(f )=[∑bij(f ij ′- f ij)+∑bij(f ij ′- f ij)] = ∑bij -∑bij 即沿着关于可行流 f 的增广链μ,增加一个单位运量时,所增加的总 费用是μ上所有前向弧的费用之和减去所有后向弧的费用之和。 我们称此费用为该增广链μ的费用。 可以证明:若 f 是流量为v(f )的所有可行流中费用最小者,而μ 是关于f 的所有增广链中费用最小的增广链,那么沿着μ去调整 f , 得到的可行流f ′就是流量为v(f ′)的所有可行流中的最小费用流。这 样,当 f ′是最大流时,它就是我们所要求的最小费用最大流。 上述命题为我们提供了寻找最小费用最大流的思路:先找一个 最小费用可行流,再找出关于该可行流的最小费用增广链,沿此链 调整流量,则得到一个新的流量增大了的最小费用流,然后对新的 最小费用流重复上述方法,一直调整到网络的最大流出现为止,便 得到了所考虑网络的最小费用最大流。 μ+ μ - μ+ μ -

由于b≥0,所以f={0}必是流量为0的最小费用流。这样, 总可以从子={0}开始算起。一般地,如果已知∫是流量为(f)的最 小费用流,余下的问题就是如何去寻找关于f的最小费用增广链。 为此,构造一个有向费用网络W(∫),它的顶点与原网络完 全相同,而把原网络中的每一条弧(,)分解成方向相反的两条 弧,即(,y)和(V,)。并按如下规则定义W(f)中弧的权数: 当y,令仅数w,者 「b,若f∠c 当弧是原D中弧y的反向弧时,令权数w若》 上述定义式的含义是:在增广链的前向弧上,当f<©时,荪瑁 加流量,其单位费用为b,当=c,时不能再增加流量,香则要花 费高昂的代价,因此单位费用为+0。在增广链的后向弧上,当 0时,减少一个单位流量可节约的费用为b,当0时,由于无法 减少流量,因此单位费用亦为+0。 经上述处理后,在费用、容量网络中寻找关于f的最小费用增厅 链问题,就转化为在有向费用网络W(f)中寻找从?,→,以费用 表示的最短路。因是求最短路,故华=+∞的弧可以从网络中省略
由于bij ≥0,所以 f ={0}必是流量为0的最小费用流。这样, 总可以从 f ={0}开始算起。一般地,如果已知 f 是流量为v(f )的最 小费用流,余下的问题就是如何去寻找关于 f 的最小费用增广链。 为此,构造一个有向费用网络W( f ),它的顶点与原网络完 全相同,而把原网络中的每一条弧(vi ,vj)分解成方向相反的两条 弧,即(vi ,vj)和(vj , vi )。并按如下规则定义W( f )中弧的权数: 上述定义式的含义是:在增广链的前向弧上,当 f ij < cij 时,可以增 加流量,其单位费用为bij ,当 f ij =cij 时不能再增加流量,否则要花 费高昂的代价,因此单位费用为+∞。在增广链的后向弧上,当 f ij> 0时,减少一个单位流量可节约的费用为bij ,当 f ij=0时,由于无法 减少流量,因此单位费用亦为+∞。 经上述处理后,在费用、容量网络中寻找关于 f 的最小费用增广 链问题,就转化为在有向费用网络W( f )中寻找从vs →vt 以费用 表示的最短路。因是求最短路,故wij = +∞的弧可以从网络中省略。 ( ) + = = ij ij ij ij ij f c b f c 若 若 当弧 D时,令权数 , , vi ,vj wij ( ) ( ) + = = , 0 - , 0 v ,v v ,v wji j i i j ij ij ij f b f 若 若 当弧 是原D中弧 的反向弧时,令权数

具体算法步骤如下: (1)取0流为初始最小费用可行流f0,即v(f0)=0: (2)若在k-1步(k=1,2,…)得最小费用流f1,则构造关于f1的有 向费用网络W(fk1); (3)在网络W(fk)中寻找从v,→v,的最短路。若不存在最短路, 则f已是最小费用最大流,计算停止。否则转(4): (④)在原网络图中与这条最短路相应的增广链上,对流量v() 进行调整,调整量为: 0-min (min (c)min) 调整后得新的最小费用流f,其流量为v(f)+0。用f代替f返回 (2)
具体算法步骤如下: ⑴取0流为初始最小费用可行流 f 0 ,即v(f 0 )=0; ⑵若在k-1步(k=1,2, …)得最小费用流 f k-1 ,则构造关于f k-1的有 向费用网络W(f k-1); ⑶在网络W(f k-1)中寻找从vs →vt 的最短路。若不存在最短路, 则 f k-1已是最小费用最大流,计算停止。否则转⑷; ⑷在原网络图中与这条最短路相应的增广链上,对流量v(f k-1 ) 进行调整,调整量为: θ=min{min( cij -f ij k-1),min f ij k-1 } 调整后得新的最小费用流 f k,其流量为v(f k-1 )+θ。用f k代替f k-1返回 ⑵ 。 μ+ μ -
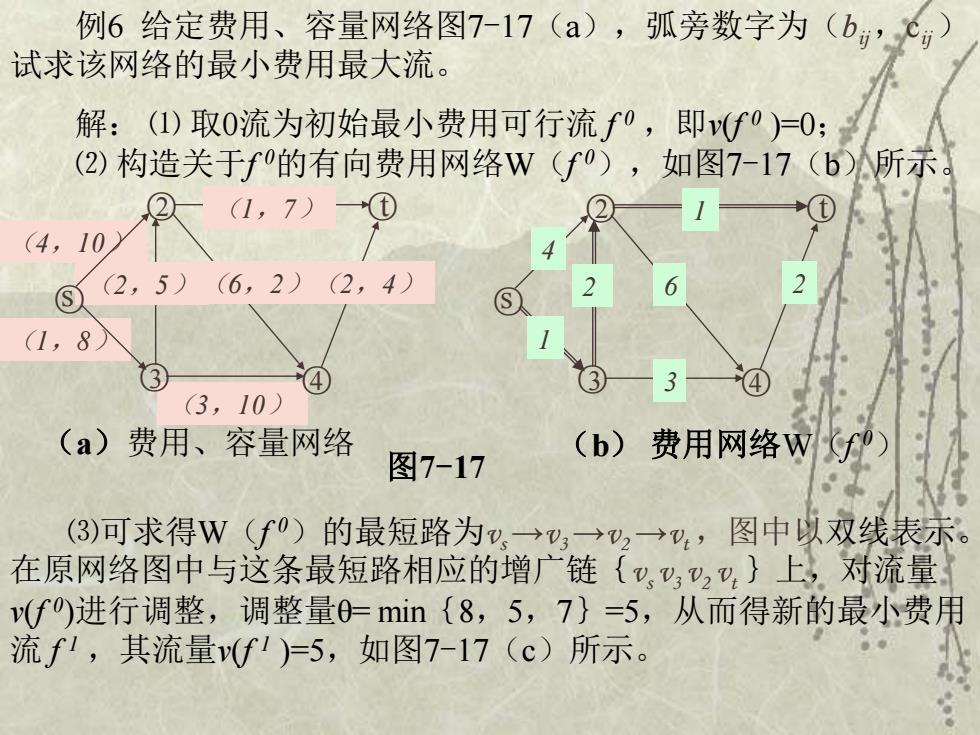
例6给定费用、容量网络图7-17(a),弧旁数字为(b,c,) 试求该网络的最小费用最大流。 解:(1)取0流为初始最小费用可行流f0,即v(f0)=0: (2)构造关于f的有向费用网络W(f),如图7-17(b)所示 4.10 (1,7)① ⑤2,5)6,2)(2,4 (1,8 (3,10) (a)费用、容量网络 图7-17 (b)费用网络Wf) (3)可求得W(f0)的最短路为,→,→v,→,图中以双线表赤。 在原网络图中与这条最短路相应的增广链(,,,,}上,对流量 v(f)进行调整,调整量0-min{8,5,7}=5,从而得新的最小费用 流f1,其流量v(f1)=5,如图7-17(c)所示
例6 给定费用、容量网络图7-17(a),弧旁数字为(bij ,cij ) 试求该网络的最小费用最大流。 解: ⑴ 取0流为初始最小费用可行流 f 0 ,即v(f 0 )=0; ⑵ 构造关于f 0的有向费用网络W(f 0),如图7-17(b)所示。 ○ ○ s 2 t (2,5)(6,2)(2,4) (4,10) ○ (1,8) (1,7) (3,10) ○3 ○4 (a)费用、容量网络 ○ ○ s 2 t 2 6 2 ○ 1 ○3 3 ○4 (b) 费用网络W(f 0) 1 4 图7-17 ⑶可求得W(f 0)的最短路为vs →v3 →v2 →vt ,图中以双线表示。 在原网络图中与这条最短路相应的增广链{vs v3 v2 vt }上,对流量 v(f 0 )进行调整,调整量θ= min{8,5,7}=5,从而得新的最小费用 流 f 1 ,其流量v(f 1 )=5,如图7-17(c)所示
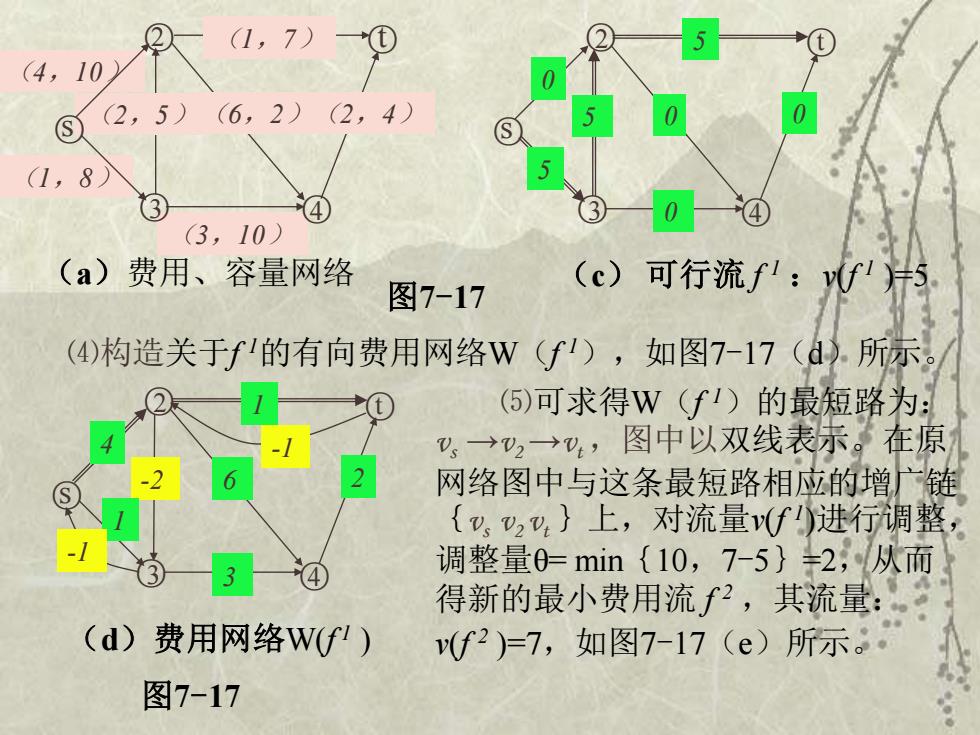
4,10/ 1,7) ③2,5)(6,2)(2,4) (1,8) (3,10) (a)费用、容量网络 图7-17 (c)可行流f':f5 (4)构造关于f'的有向费用网络W(f),如图7-17(d)所示。 (⑤)可求得W(f1)的最短路为: 巴,→→4,图中以双线表赤。在原 2 网络图中与这条最短路相应的增广链 {,24,}上,对流量v(f)进行调整, 调整量0min{10,7-5}2,从而 得新的最小费用流f2,其流量: (d)费用网络W(f') (f2)=7,如图7-17(e)所示。 图7-17
s (2,5)(6,2)(2,4) ○ (1,7) (3,10) ○3 ○4 (a)费用、容量网络 s 2 5 0 0 ○ 5 ○3 0 ○4 (c) 可行流 f 1 :v(f 1 )=5 5 0 图7-17 ○2 ○t ○ ○t ⑷构造关于f 1的有向费用网络W(f 1),如图7-17(d)所示。 (4,10) (1,8) s 2 -2 6 2 ○ 1 ○3 3 ○4 (d)费用网络W(f 1 ) 1 4 ○ ○t -1 -1 图7-17 ⑸可求得W(f 1)的最短路为: vs →v2 →vt ,图中以双线表示。在原 网络图中与这条最短路相应的增广链 {vs v2 vt }上,对流量v(f 1 )进行调整, 调整量θ= min{10,7-5}=2,从而 得新的最小费用流 f 2 ,其流量: v(f 2 )=7,如图7-17(e)所示
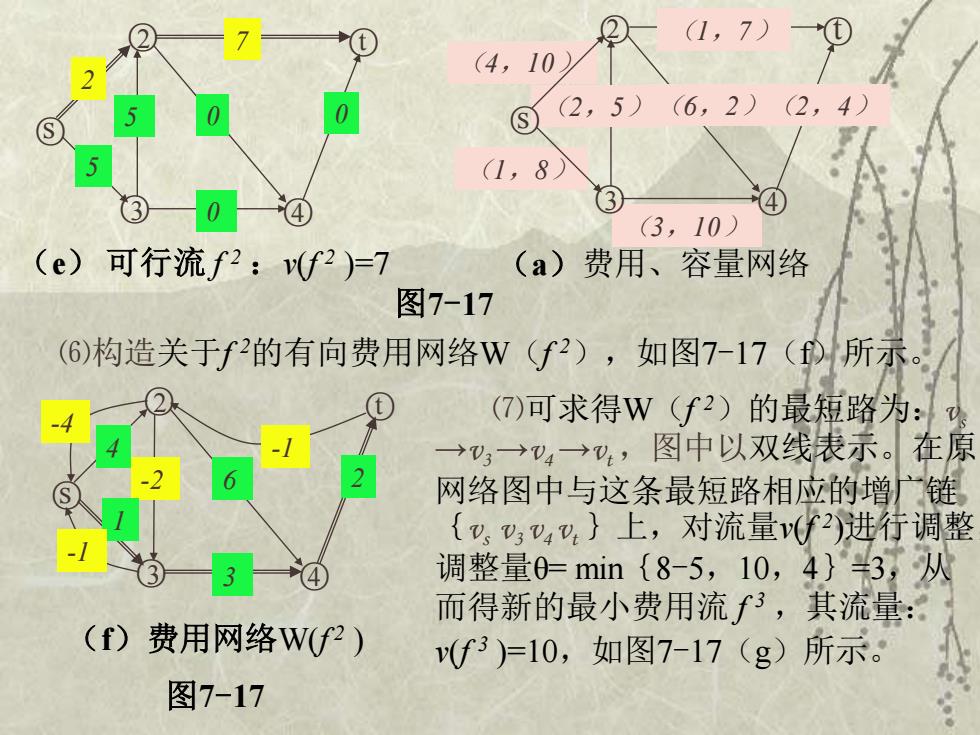
2 (1,7) (4,10) (2,5)(6,2)(2,4) (1,8) 3 (3,10) (e)可行流f2:v(f2)=7 (a)费用、容量网络 图7-17 (6)构造关于f的有向费用网络W(f2),如图7-17()所示。 (7)可求得W(f2)的最短路为: →→v4→,图中以双线表示。在原 2 网络图中与这条最短路相应的增广链 {飞,Vv,}上,对流量v(f2)进行调整 4 调整量0-min(8-5,10,4}3;从 而得新的最小费用流f,其流量: (f)费用网络W(f2) v(f3)=10,如图7-17(g)所示。 图7-17
s 2 5 0 0 ○ 7 ○3 0 ○4 5 2 ○ ○t (e) 可行流 f 2 :v(f 2 )=7 s (2,5)(6,2)(2,4) ○ (1,7) (3,10) ○3 ○4 (a)费用、容量网络 ○2 ○t (4,10) (1,8) 图7-17 ⑹构造关于f 2的有向费用网络W(f 2),如图7-17(f)所示。 s 2 -2 6 2 ○ ○3 3 ○4 (f)费用网络W(f 2 ) 1 4 ○ ○t -1 -1 -4 ⑺可求得W(f 2)的最短路为:vs →v3 →v4 →vt ,图中以双线表示。在原 网络图中与这条最短路相应的增广链 {vs v3 v4 vt }上,对流量v(f 2 )进行调整, 调整量θ= min{8-5,10,4}=3,从 而得新的最小费用流 f 3 ,其流量: v(f 3 )=10,如图7-17(g)所示。 图7-17
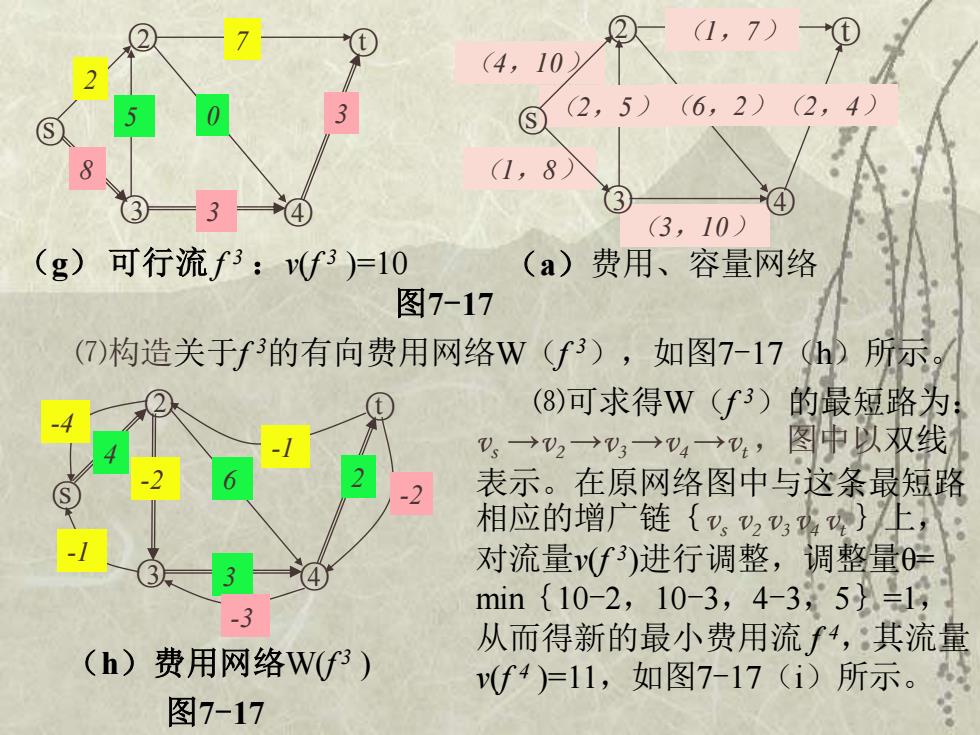
(1,7) (t (4,10/ 3 (2,5) (6,2)(2,4) 1,8) 3 (3,10) (g)可行流f3:v(f3)=10 (a)费用、容量网络 图7-17 (7)构造关于f3的有向费用网络W(f3),如图7-17 所示 (8)可求得W(f3)的最短路为: ”,→2→→v,→,图中以双线 表示。在原网络图中与这条最短路 相应的增广链{V,2V)生, 对流量(f3)进行调整,调整量0 -3 min{10-2,10-3,4-3,5=1, 从而得新的最小费用流+,其流量 (h)费用网络W(f3) (f4)=11,如图7-17(i)所示。 图7-17
s 2 5 0 3 ○ 7 ○3 3 ○4 8 2 ○ ○t (g) 可行流 f 3 :v(f 3 )=10 ⑺构造关于f 3的有向费用网络W(f 3),如图7-17(h)所示。 s (2,5)(6,2)(2,4) ○ (1,7) (3,10) ○3 ○4 (a)费用、容量网络 ○2 ○t (4,10) (1,8) 图7-17 s 2 -2 6 2 ○ ○3 3 ○4 (h)费用网络W(f 3 ) 4 ○t -1 -1 -4 图7-17 ○ -3 -2 ⑻可求得W(f 3)的最短路为: vs →v2 →v3 →v4 →vt ,图中以双线 表示。在原网络图中与这条最短路 相应的增广链{vs v2 v3 v4 vt }上, 对流量v(f 3 )进行调整,调整量θ= min{10-2,10-3,4-3,5}=1, 从而得新的最小费用流 f 4 ,其流量 v(f 4 )=11,如图7-17(i)所示

7 (4,10 ”9 ⑨ (2,5)(6,2)(2,4) (1,8) 4 4 (3,10) (i) 可行流f4:vf4)=11 (a)费用、容量网络 图7-17 ① (7)构造关于f的有向费用网络 W(f),如图7-17(j)所示: -2 由于在W(f)中无法找到从→ 的最短路,所以∫4就是该网终的最 小费用最大流,流量(f)=1,其 -3 分布情况如图7-17()所示。它对 (j)费用网络W(f) 应的总费用为: b()=4×3+1×7+1×8+2×4+2×4+3X4=55
s 2 4 0 4 ○ 7 ○3 4 ○4 8 3 ○ ○t (i) 可行流 f 4 :v(f 4 )=11 s (2,5)(6,2)(2,4) ○ (1,7) (3,10) ○3 ○4 (a)费用、容量网络 ○2 ○t (4,10) (1,8) 图7-17 ⑺构造关于f 4的有向费用网络 W(f 4),如图7-17(j)所示。 由于在W(f 4)中无法找到从vs →vt 的最短路,所以 f 4 就是该网络的最 小费用最大流,流量v(f 4 )=11,其 分布情况如图7-17(i)所示。它对 应的总费用为: s 2 -2 6 ○ ○3 3 ○4 (j)费用网络W(f 4 ) 4 t -1 -1 -4 -3 -2 ○ ○ 2 b(f 4 )=4×3+1×7+1×8+2×4+2×4+3×4=55