
@ §6中国邮递员问题 →6.1欧拉图 欧拉图问题起源与著名的哥尼斯堡七桥问题,它的 实质是如何判断一个连通图能否一笔不重复地画出。这 个问题是由大数学家欧拉解决的,所以称为欧拉图问题。 力 定义:给一个连通多重图G,若存在一条链(圈) 过每边一次且仅一次,则称这条链(圈)为欧拉链 (圈)。 定义:一个图如果存在欧拉圈,则称之为欧拉图。 显然,一个图若能一笔不重复地画出,则这个图就是 欧拉图或含有欧拉链。 定理:连通多重图G是欧拉图,当且仅当图中无奇 点
§6 中国邮递员问题 6.1 欧拉图 欧拉图问题起源与著名的哥尼斯堡七桥问题,它的 实质是如何判断一个连通图能否一笔不重复地画出。这 个问题是由大数学家欧拉解决的,所以称为欧拉图问题。 定义:给一个连通多重图G,若存在一条链(圈) 过每边一次且仅一次,则称这条链(圈)为欧拉链 (圈)。 定义:一个图如果存在欧拉圈,则称之为欧拉图。 显然,一个图若能一笔不重复地画出,则这个图就是 欧拉图或含有欧拉链。 定理:连通多重图G是欧拉图,当且仅当图中无奇 点

这个定理的结论是显然的,因为欧拉图从某一点出 发又回到原来的出发点,这就要求与每个顶点相关联的 边数应是偶数,从而才能保证从一条边进入该点,从与 该点相关联的另一条边出去。 推论:连通多重图G有欧拉链,当且仅当G恰有两 个奇点。 上面的定理和推论提供了识别一个图能否一笔不重 复画出的简单方法。如图7-18,有两个奇点,所以能 笔不重复地画出,从奇点,开始一笔画到奇点y,。 V V V2 V4 06 图7-18
这个定理的结论是显然的,因为欧拉图从某一点出 发又回到原来的出发点,这就要求与每个顶点相关联的 边数应是偶数,从而才能保证从一条边进入该点,从与 该点相关联的另一条边出去。 推论:连通多重图G有欧拉链,当且仅当G恰有两 个奇点。 上面的定理和推论提供了识别一个图能否一笔不重 复画出的简单方法。如图7-18,有两个奇点,所以能一 笔不重复地画出,从奇点v2开始一笔画到奇点v5 。 图7-18 · · v1 v2 v3 v4 v5 v6

6.2中国邮递员问题 邮递员每次要走遍他所负责街区的每一条道路,投递 完毕后仍须回到邮局,他应走什么路线才能使总路程最短 这个问题是由我国山东师范学院管梅谷教授在1962年首次 提出的,所以国际上通称为中国邮递员问题。 中国邮递员问题可以抽象为一个连通图,每个边都有 一个非负权数,试求一个圈,过每边至少一次,并使圈的 总权数最小。 解此问题的基本思路是:若街区路无奇点,显然按欧 拉图定理可以不重复地走遍所有街道回到出发位置。如果 图中有奇点,每边只走一次又回到出发点是不可能的。如 果要回到原地就得走些重复路,也就是在原来的街区图上 添加一些边,使有奇点的图转换成无奇点的图。由于我们 要求总权数最小,所以必须寻找使新增加的边的总权数最 小的方案。我们称增加重复边使图中无奇点的方案为可行 方案,称总权数最小的方案为最优方案
6.2 中国邮递员问题 邮递员每次要走遍他所负责街区的每一条道路,投递 完毕后仍须回到邮局,他应走什么路线才能使总路程最短。 这个问题是由我国山东师范学院管梅谷教授在1962年首次 提出的,所以国际上通称为中国邮递员问题。 中国邮递员问题可以抽象为一个连通图,每个边都有 一个非负权数,试求一个圈,过每边至少一次,并使圈的 总权数最小。 解此问题的基本思路是:若街区路无奇点,显然按欧 拉图定理可以不重复地走遍所有街道回到出发位置。如果 图中有奇点,每边只走一次又回到出发点是不可能的。如 果要回到原地就得走些重复路,也就是在原来的街区图上 添加一些边,使有奇点的图转换成无奇点的图。由于我们 要求总权数最小,所以必须寻找使新增加的边的总权数最 小的方案。我们称增加重复边使图中无奇点的方案为可行 方案,称总权数最小的方案为最优方案

般先确定一个可行方案,然后不断改善可行方案 就能求出最优方案。具体作法如下: 1.确定可行方案 一个连通图中,若有奇点,则奇点个数必为偶数。 把奇点配对后,沿连接每对奇点的链增加重复边,则新 图中没有奇点,这样,带有重复边的新图就是可行方案。 2.调整可行方案 可以证明最优方案具有下述两条性质,并可以按这 两条性质不断调整可行方案,直至获得最优方案。 (1)最优方案中,每一条边上最多有一条重复边。 如果可行方案中,某条边重复边多于一条,则可以 成对减去重复边,直至满足该性质。 (2)最优方案的图中,每个圈上的重复边权数之和不 大于该圈总权数的一半。否则,将该圈上的重复边去掉
一般先确定一个可行方案,然后不断改善可行方案 就能求出最优方案。具体作法如下: 1.确定可行方案 一个连通图中,若有奇点,则奇点个数必为偶数。 把奇点配对后,沿连接每对奇点的链增加重复边,则新 图中没有奇点,这样,带有重复边的新图就是可行方案。 2.调整可行方案 可以证明最优方案具有下述两条性质,并可以按这 两条性质不断调整可行方案,直至获得最优方案。 ⑴最优方案中,每一条边上最多有一条重复边。 如果可行方案中,某条边重复边多于一条,则可以 成对减去重复边,直至满足该性质。 ⑵最优方案的图中,每个圈上的重复边权数之和不 大于该圈总权数的一半。否则,将该圈上的重复边去掉

给圈上原来没有重复边的边加上重复边,则图中仍无奇 点,而且重复边的总权数下降。 例7求如图7-19所示的街路的中国邮递员问题。 3 V; 4 Vs 3 2 2 V2 1 Vo 4 图7-19 解:图中有四个奇点v,V。,将它们配对,V,为一对, v。为一对。沿[v,,]增加重复边,沿[4,,]增加重复边, 得可行方案如图7-20所示
给圈上原来没有重复边的边加上重复边,则图中仍无奇 点,而且重复边的总权数下降。 例7 求如图7-19所示的街路的中国邮递员问题。 图7-19 v1 v2 v3 v4 v5 v6 v7 v8 1 1 1 3 3 2 2 4 4 4 解:图中有四个奇点v3v4v5v6 ,将它们配对,v3v5 为一对, v4v6 为一对。沿[v3,v5]增加重复边,沿[v4,v6]增加重复边, 得可行方案如图7-20所示
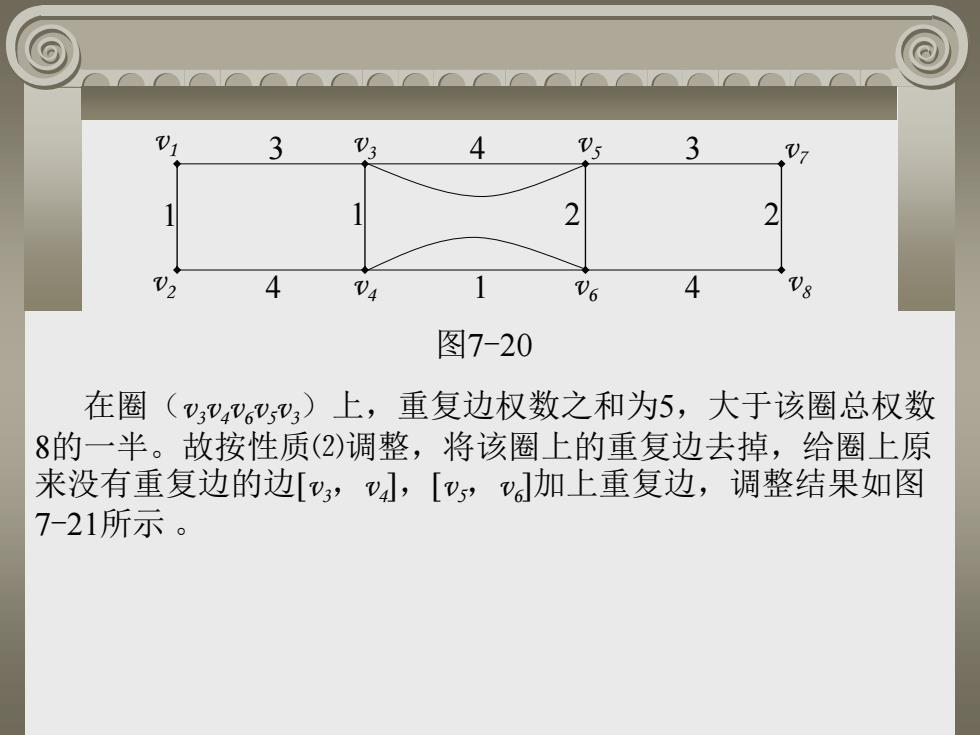
0 3 V: 4 Vs 3 2 2 4 V4 4 08 图7-20 在圈(,wV,,W)上,重复边权数之和为5,大于该圈总权数 8的一半。故按性质(2)调整,将该圈上的重复边去掉,给圈上原 来没有重复边的边[v,,[v,v,加上重复边,调整结果如图 7-21所示
图7-20 v1 v2 v3 v4 v5 v6 v7 v8 1 1 1 3 3 2 2 4 4 4 在圈(v3v4v6v5v3)上,重复边权数之和为5,大于该圈总权数 8的一半。故按性质⑵调整,将该圈上的重复边去掉,给圈上原 来没有重复边的边[v3,v4 ],[v5,v6 ]加上重复边,调整结果如图 7-21所示

V; 4 Vs 3 2 2 V2 4 4 Vs 图7-21 检查图7-21,该方案无奇点,而且满足最优解的性质(1)、(2), 于是图7-21已是最优方案,重复边总权数为3。 以上介绍的求最优邮递路线的方法,通常称为奇偶点图上作 业法。该方法的困难在于检查图中的每一个圈,当图中点数、边 数较大时,圈的个数将会很多
图7-21 v1 v2 v3 v4 v5 v6 v7 v8 1 1 1 3 3 2 2 4 4 4 检查图7-21,该方案无奇点,而且满足最优解的性质⑴、⑵, 于是图7-21已是最优方案,重复边总权数为3。 以上介绍的求最优邮递路线的方法,通常称为奇偶点图上作 业法。该方法的困难在于检查图中的每一个圈,当图中点数、边 数较大时,圈的个数将会很多

第七章作业 +P137:2 +P137:4 +P139:91) →P140:11 →P140:13
第 七 章 作 业 P137:2 P137:4 P139:9⑴ P140:11 P140:13