§2树与最小部分树 2.1树的概念 树是一种简单而且有用的图。早在1847年克希霍夫研 究电网络时,便发展了有关树的理论。树在分子结构、电 i 网络分析及企业管理、优化设计等方面都有很重要的作用。 树:无圈的连通图就称为树。 例如5个顶点构成的无圈连通图是下列树枝形状。 “树”的名称即由此而来。 (a) (b) 图7-7
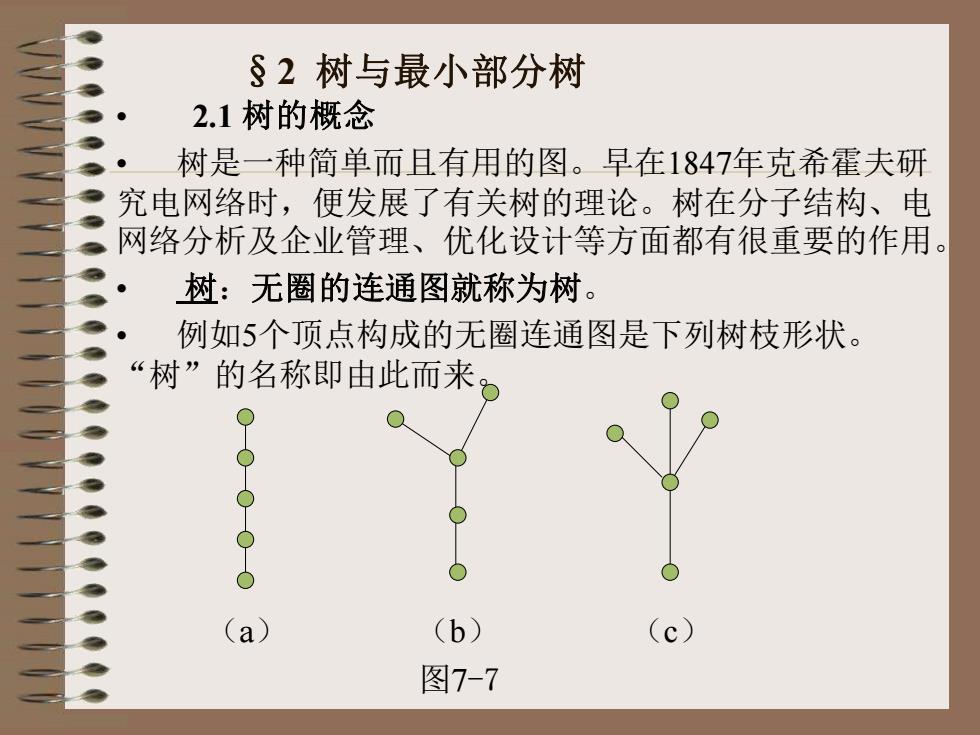
§2 树与最小部分树 • 2.1 树的概念 • 树是一种简单而且有用的图。早在1847年克希霍夫研 究电网络时,便发展了有关树的理论。树在分子结构、电 网络分析及企业管理、优化设计等方面都有很重要的作用。 • 树:无圈的连通图就称为树。 • 例如5个顶点构成的无圈连通图是下列树枝形状。 “树”的名称即由此而来。 (a) (b) (c) 图7-7
树是实际活动中最常用的图。图7-8表示由通信线路 二连接起来的逐级辐射通信网,还可以理解为图书目录分类、 。质量指标因果分析图等。 OC QD QE OF OG QH K Q 图7-8
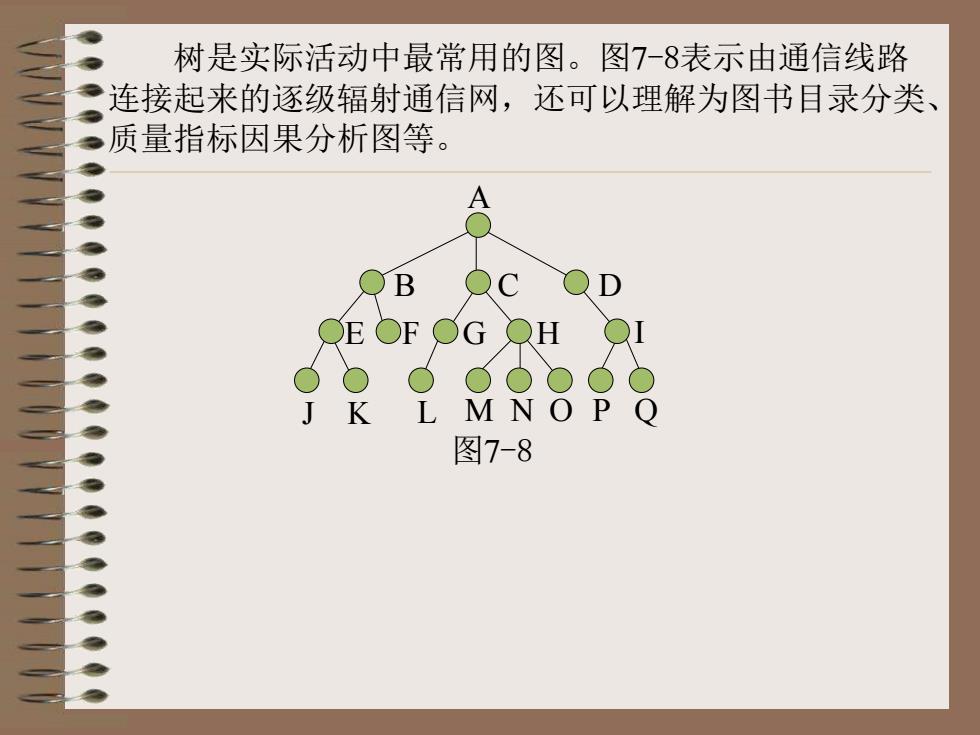
树是实际活动中最常用的图。图7-8表示由通信线路 连接起来的逐级辐射通信网,还可以理解为图书目录分类、 质量指标因果分析图等。 A B C D E F G H I J K L M N O P Q 图7-8
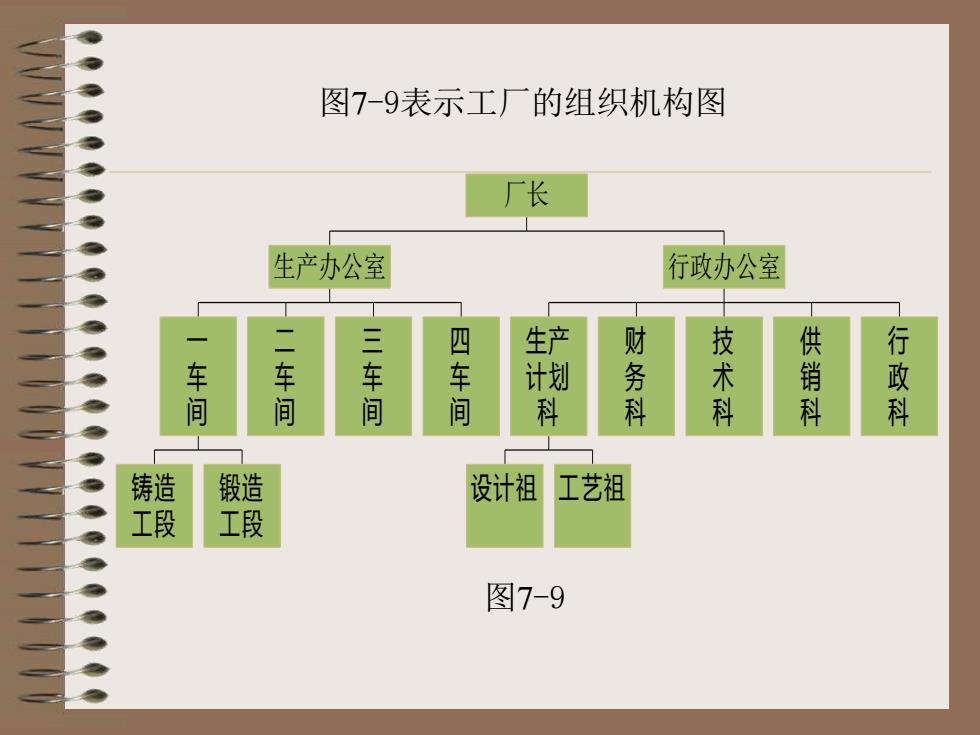
图7-9表示工厂的组织机构图 长 生产办公室 行政办公室 车间 二车间 三车间 四车间 科 财务科 技术科 供销科 行政科 铸造 锻造 设计祖 工艺祖 工段 工段 图7-9
图7-9表示工厂的组织机构图 铸 造 工 段 锻 造 工 段 一 车 间 二 车 间 三 车 间 四 车 间 生产办公室 设计祖 工艺祖 生 产 计 划 科 财 务 科 技 术 科 供 销 科 行 政 科 行政办公室 厂长 图7-9

从树的定义可以推出以下几点性质: 性质1设T=(V,E)是一个树,p(T)≥2, 则T中 至少有两个悬挂点。 证明:令L={v,V2…V)是T中含边数最多的一条链, 因p(T)≥2,故链L中至少含两个点,从而v,≠。现在证 明是悬挂点,即d(,)=1。若d()≥2,则至少存在 边[vnvm],使m≠2.若vn不在L上,则{vm2…}是比L多 条边的链,与L是含边数最多的链矛盾。若vm在L上,则 {v…vmy}是T中的一个圈,这与T是树矛盾,于是必 有d (v)=1,即v,是悬挂点。同理可证v也是悬挂点。 性质2含有p个顶点的树中恰有p-1条边。 证明:当p=1,2时,结论显然成立。 假设p=k时结论成立,即有k-1条边。当p=k+1时,去 掉一个悬挂边及与它关联的悬挂点,显然所得图仍是树, 而且含有k个顶点k-1条边,所以,p=k+1的树应有k条边。 综上,由数学归纳法,结论得证
从树的定义可以推出以下几点性质: 性质1 设T=(V,E)是一个树,p(T)≥2,则T中 至少有两个悬挂点。 证明:令L={v1v2…vk }是T中含边数最多的一条链, 因p(T)≥2,故链L中至少含两个点,从而v1≠vk。现在证 明v1是悬挂点,即d(v1)=1。若d(v1) ≥2,则至少存在 边[v1 ,vm ],使m ≠ 2.若vm不在L上,则{vmv1v2…vk}是比L多 一条边的链,与L是含边数最多的链矛盾。若vm在L上,则 {v1v2…vmv1}是T中的一个圈,这与T是树矛盾,于是必 有d(v1)=1,即v1是悬挂点。同理可证vk也是悬挂点。 性质2 含有p个顶点的树中恰有p-1条边。 证明:当p=1,2时,结论显然成立。 假设p=k时结论成立,即有k-1条边。当p=k+1时,去 掉一个悬挂边及与它关联的悬挂点,显然所得图仍是树, 而且含有k个顶点k-1条边,所以,p=k+1的树应有k条边。 综上,由数学归纳法,结论得证
性质3 图G是树的充要条件是任意两点之间有且仅有 条链。 2.2 图的部分树 定义:设图T=(V,E')是图G=(V,E)的部分图, 如果是T=(V,E')是树,则称T为G的部分树。 例如图7-10中,(b)是(a)的 一个部分树。 0 V 06 06 02 05 a b 图7-10
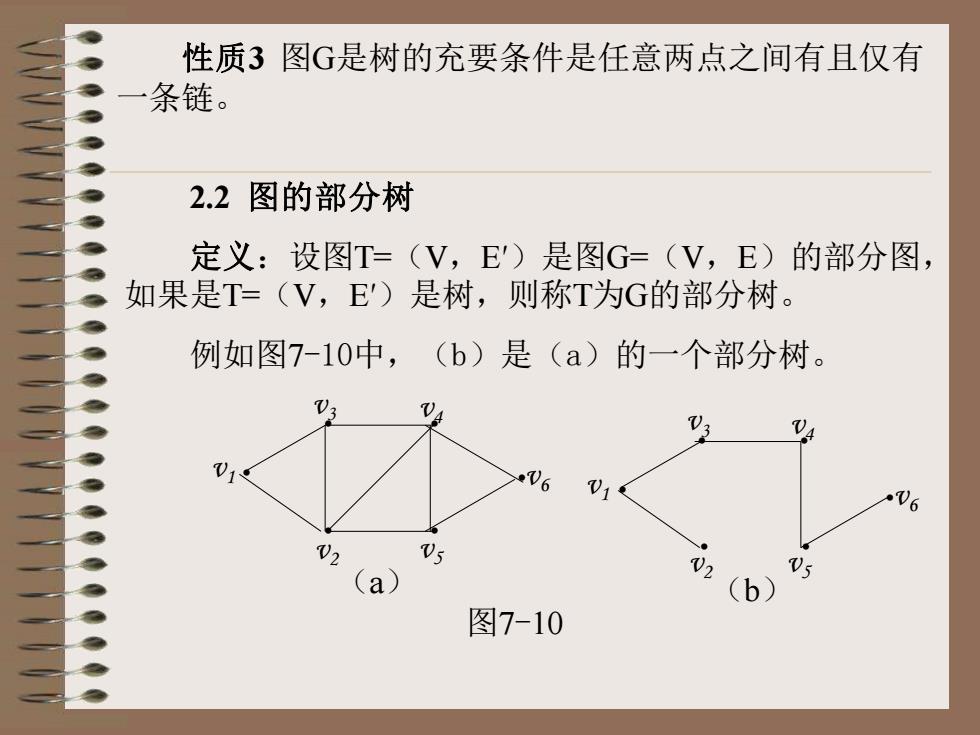
性质3 图G是树的充要条件是任意两点之间有且仅有 一条链。 2.2 图的部分树 定义:设图T=(V,E′)是图G=(V,E)的部分图, 如果是T=(V,E′)是树,则称T为G的部分树。 例如图7-10中,(b)是(a)的一个部分树。 · · · · · v1 · v2 v3 v4 v5 (a) v6 v3 · · · · · · v4 v5 v6 v1 v2(b) 图7-10

定理3图G有部分树的充分必要条件是图G是连通图。 证明:必要性是显然的。 充分性:设图G是连通图,如果G不含圈,那么G本 身是树,从而G是它自身的部分树。若G含圈,任取一个 圈,去掉圈上的任一条边,则余下的图仍是连通图,如果 这时图中无圈,则已得G的一个部分树,否则重复以上作 法,最终可得到G的一个部分树。 定理3的证明提供了一个寻找部分树的方法,即 破圈法:在连通图G中任取一个圈,去掉圈上的任 条边,对余下的图重复这个步骤,直至无圈为止。 还可以采取另外的方法寻找部分树。 避圈法:每次增加一条边e∈E,且与已有边不构成圈, 直至恰有p-1条边为止
定理3 图G有部分树的充分必要条件是图G是连通图。 证明:必要性是显然的。 充分性:设图G是连通图,如果G不含圈,那么G本 身是树,从而G是它自身的部分树。若G含圈,任取一个 圈,去掉圈上的任一条边,则余下的图仍是连通图,如果 这时图中无圈,则已得G的一个部分树,否则重复以上作 法,最终可得到G的一个部分树。 定理3的证明提供了一个寻找部分树的方法,即 破圈法:在连通图G中任取一个圈,去掉圈上的任一 条边,对余下的图重复这个步骤,直至无圈为止。 还可以采取另外的方法寻找部分树。 避圈法:每次增加一条边e ∈E,且与已有边不构成圈, 直至恰有p-1条边为止

2.3最小部分树 定义:给图G= (V,E),对G的每条边[,y],相应 有一个数o,则称这样的图G为赋权图,称o为边[,y]上 的权。 这里所说的“权”, 根据实际问题需要,可以赋予它 不同的含义,例如表示距离、时间、费用等等。赋权图不 仅指出各个点之间的邻接关系,而且也表示出各点之间的 数量关系。所以赋权图在工程技术及科学管理中有广泛的 应用 最小部分树就是赋权图上最优化问题之一。 定义:给连通图G=(V,E),对每一边∈E,有 权≥0,最小部分树问题就是求一个部分树T*,使 0( T*)=w%达到最小。 和求部分树一样,求最小部分树也有破圈法和避圈法。 破圈法:每次去掉圈上权数最大的边,直至无圈为止。 避圈法:每次取权数最小且与已取的边不构成圈的边, 直至恰有p-1条边为止
2.3 最小部分树 定义:给图G=(V,E),对G的每条边[vi ,vj ],相应 有一个数ωij ,则称这样的图G为赋权图,称ωij 为边[vi ,vj ]上 的权。 这里所说的“权”,根据实际问题需要,可以赋予它 不同的含义,例如表示距离、时间、费用等等。赋权图不 仅指出各个点之间的邻接关系,而且也表示出各点之间的 数量关系。所以赋权图在工程技术及科学管理中有广泛的 应用。最小部分树就是赋权图上最优化问题之一。 定义:给连通图G=(V,E),对每一边e∈E,有一 权ω≥0,最小部分树问题就是求一个部分树T﹡,使 ω(T﹡)= e T ω (e) 达到最小。 和求部分树一样,求最小部分树也有破圈法和避圈法。 破圈法:每次去掉圈上权数最大的边,直至无圈为止。 避圈法:每次取权数最小且与已取的边不构成圈的边, 直至恰有p-1条边为止

例1今要在七个城市之间修筑一个公路网,每两个城 市之间的公路修筑费用就是各条边上的权,见图7-11。试 二求总修筑费用最小的公路网。 V 3V5 2 03 4 10 5 5 6 图7-11 01 图7-12 解:(I)破圈法:从圈{v,,w,}中去掉边[,小;从 圈{V}中去掉边[6,小从圈{}中去掉边 [y,:从圈{2}中去掉边[,v;从圈{vV} 中去掉边[v1,]:从圈{v}中去掉边[v4,,得最小 树T*如图7-12,其总权数为0(T*)=2+3+4+3+4+5=21. (2)避圈法:依次选取边[v4,v],[,小,[1,vd, [v5,V6d, 二[v2,v小, [2,],画出这棵最小树仍同图7-12
例1 今要在七个城市之间修筑一个公路网,每两个城 市之间的公路修筑费用就是各条边上的权,见图7-11。试 求总修筑费用最小的公路网。 v2 v4 v5 v6 v1 v3 v7 图7-11 10 8 3 4 3 4 5 5 2 7 6 6 解:⑴破圈法:从圈{v1v6v7v1}中去掉边[v1 ,v7 ];从 圈{v5v6v7v5}中去掉边[v6 ,v7 ];从圈{v3v4v6v3}中去掉边 [v3 ,v4 ];从圈{v2v3v6v2}中去掉边[v3 ,v6 ];从圈{v1v2v6v1} 中去掉边[v1 ,v2 ];从圈{v4v5v6v4}中去掉边[v4 ,v6 ],得最小 树T﹡如图7-12,其总权数为ω(T﹡)=2+3+4+3+4+5=21。 ⑵避圈法:依次选取边[v4 ,v5 ], [v5 ,v7 ], [v1 ,v6 ],[v5 ,v6 ], [v2 ,v6 ], [v2 ,v3 ],画出这棵最小树仍同图7-12。 v7 v5 v4 v6 v1 v2 v3 图7-12 3 3 4 4 2 5