
图的理论研究已经有几百年的历史,但将它广泛地应用于 工程技术和生产管理那还是近几十年的事。例如,各种通讯网 络和计算机网络的优化设计,交通网络的合理分布及大型工程 项目的计划管理都需要运用图论网络分析方法才能有效地解决。 此外,它在化学、物理学、控制论、信息论、系统工程等方面 都有很重要的应用。因此图论是运筹学一个十分重要的分支。 图论的奠基人是欧拉,他于1736年发表了图论方面的第一 篇论文,其中讨论了下述著名的七桥问题
图的理论研究已经有几百年的历史,但将它广泛地应用于 工程技术和生产管理那还是近几十年的事。例如,各种通讯网 络和计算机网络的优化设计,交通网络的合理分布及大型工程 项目的计划管理都需要运用图论网络分析方法才能有效地解决。 此外,它在化学、物理学、控制论、信息论、系统工程等方面 都有很重要的应用。因此图论是运筹学一个十分重要的分支。 图论的奠基人是欧拉,他于1736年发表了图论方面的第一 篇论文,其中讨论了下述著名的七桥问题
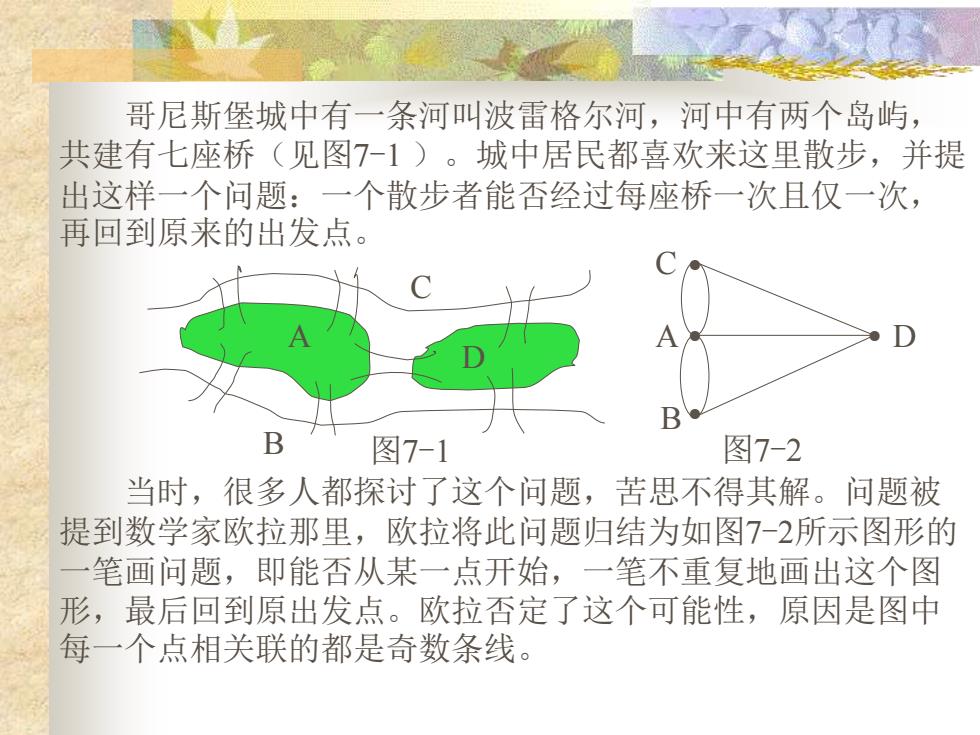
哥尼斯堡城中有一条河叫波雷格尔河,河中有两个岛屿, 共建有七座桥(见图7-1)。城中居民都喜欢来这里散步,并提 出这样一个问题:一个散步者能否经过每座桥一次且仅一次, 再回到原来的出发点。 B B 图7-1 图7-2 当时,很多人都探讨了这个问题,苦思不得其解。问题被 提到数学家欧拉那里,欧拉将此问题归结为如图7-2所示图形的 笔画问题,即能否从某一点开始,一笔不重复地画出这个图 形,最后回到原出发点。欧拉否定了这个可能性,原因是图中 每一个点相关联的都是奇数条线
哥尼斯堡城中有一条河叫波雷格尔河,河中有两个岛屿, 共建有七座桥(见图7-1 )。城中居民都喜欢来这里散步,并提 出这样一个问题:一个散步者能否经过每座桥一次且仅一次, 再回到原来的出发点。 A B C D 当时,很多人都探讨了这个问题,苦思不得其解。问题被 提到数学家欧拉那里,欧拉将此问题归结为如图7-2所示图形的 一笔画问题,即能否从某一点开始,一笔不重复地画出这个图 形,最后回到原出发点。欧拉否定了这个可能性,原因是图中 每一个点相关联的都是奇数条线。 ● ● ● A ● B C D 图7-1 图7-2
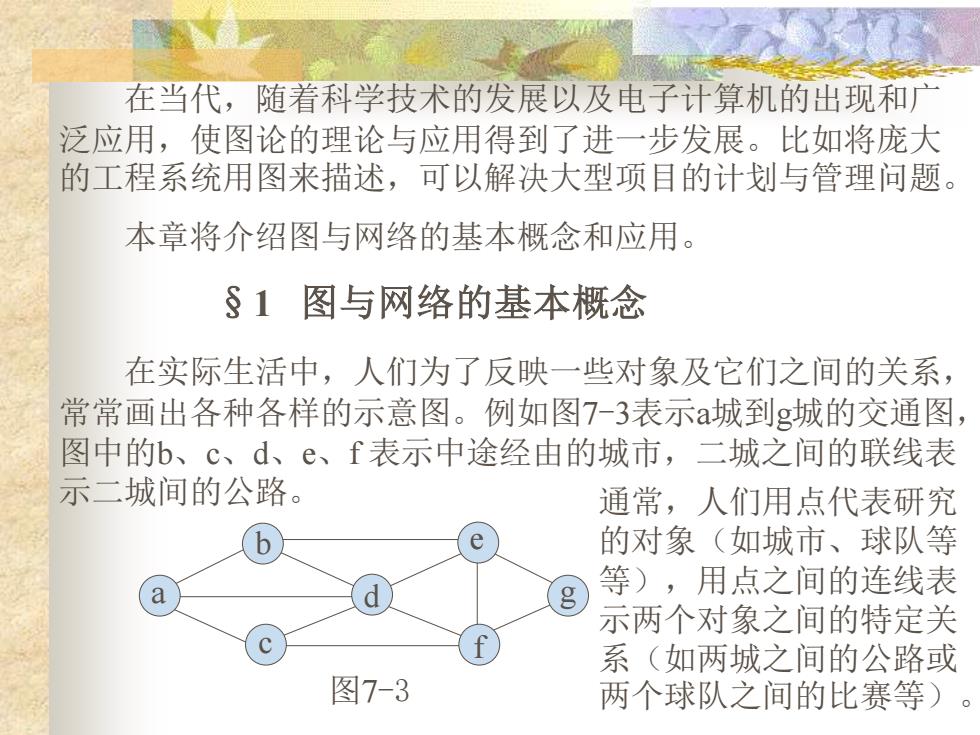
在当代,随着科学技术的发展以及电子计算机的出现和) 泛应用,使图论的理论与应用得到了进一步发展。比如将庞大 的工程系统用图来描述,可以解决大型项目的计划与管理问题。 本章将介绍图与网络的基本概念和应用。 §1图与网络的基本概念 在实际生活中,人们为了反映一些对象及它们之间的关系, 常常画出各种各样的示意图。例如图7-3表示a城到g城的交通图 图中的b、c、d、e、f表示中途经由的城市,二城之间的联线表 示二城间的公路。 通常,人们用点代表研究 的对象(如城市、球队等 等),用点之间的连线表 示两个对象之间的特定关 系(如两城之间的公路或 图7-3 两个球队之间的比赛等)
在当代,随着科学技术的发展以及电子计算机的出现和广 泛应用,使图论的理论与应用得到了进一步发展。比如将庞大 的工程系统用图来描述,可以解决大型项目的计划与管理问题。 本章将介绍图与网络的基本概念和应用。 §1 图与网络的基本概念 在实际生活中,人们为了反映一些对象及它们之间的关系, 常常画出各种各样的示意图。例如图7-3表示a城到g城的交通图, 图中的b、c、d、e、f 表示中途经由的城市,二城之间的联线表 示二城间的公路。 a b c d e f g 图7-3 通常,人们用点代表研究 的对象(如城市、球队等 等),用点之间的连线表 示两个对象之间的特定关 系(如两城之间的公路或 两个球队之间的比赛等)

般,称由一些点和一些边组成的集合为图,记作G(V,E) 其中V是点的集合,E是边的集合。图G中所含的点的个数,般起 作G);所含的边的个数,一般记作G): 图论中的图与一般的投影图是完全不同的概念。图论中的图是 反映对象之间的关系,在一般情况下,图中点的相对位置如何,点 之间连线的长短曲直,对于反映对象之间的关系并不重要。 一条联结点,y,∈V的边记作e=[,y],称,y为e的端点,称e 为,?的关联边。在图中具有同一条关联边的点称为相邻点,具有 公共端点的边称为相邻边。 某个边的两个端点相同,则称该边为还(如图7-4中的e)。若 两点之间有多于一条边相关联,则称这些边为多重边(如图7-4中 的e,e2)。一个无环、无多重边的图称为简单图,一个无环、但 有多重边的图称为多重图。点v的关联边个数称为点v的次,记作 d(v)。如图7-4中d(v)=4,d(v2)=3, d()=4,d(v4)=1,d(V)=4。 e2 称次为1的点为悬挂点,悬挂点所 e 关联的边为悬挂边。图7-4中的v为悬 e 挂点,e,为悬挂边。 06 图7-4
一般,称由一些点和一些边组成的集合为图,记作G=(V,E), 其中V是点的集合,E是边的集合。图G中所含的点的个数,一般记 作p(G);所含的边的个数,一般记作q(G)。 图论中的图与一般的投影图是完全不同的概念。图论中的图是 反映对象之间的关系,在一般情况下,图中点的相对位置如何,点 之间连线的长短曲直,对于反映对象之间的关系并不重要。 一条联结点vi ,vj∈V的边记作e =[vi ,vj ],称vi ,vj 为e 的端点,称e 为vi ,vj 的关联边。在图中具有同一条关联边的点称为相邻点,具有 公共端点的边称为相邻边。 某个边的两个端点相同,则称该边为环(如图7-4中的e8)。若 两点之间有多于一条边相关联,则称这些边为多重边(如图7-4中 的e1, e2 )。一个无环、无多重边的图称为简单图,一个无环、但 有多重边的图称为多重图。点v 的关联边个数称为点v 的次,记作 d(v )。如图7-4中d(v1)=4,d(v2)=3, d(v3)=4,d(v4)=1,d(v5)=4。 称次为1的点为悬挂点,悬挂点所 关联的边为悬挂边。图7-4中的v4 为悬 挂点,e7 为悬挂边。 · · · · · v1 v2 v v3 5 v4 e1 e2 e3 e4 e5 e e 7 8 e6 图7-4

定理1图G=(V,E)中,所有点的次数之和等于边数的两倍。 这是显然的,因为在计算各点的次时,每条边都被用了两次。 次为奇数的点,称为奇点;次为偶数的点,称为偶点。 定理2任一图中,奇点的个数必为偶数。 证明:设V和V2分别是图中奇点和偶点的集合,q为G中边的 个数,则 dw,=∑do,tΣdo,=2q v.EV v∈V, 因为,do,)是偶数,所以d,)也是偶数,从而中奇点个数必为 偶数个。 链:图G中,点边交错序列{),如果满足e[,, e[2,V3],, 则称这个点边交错序列为,到的链。 圈:=饭的链称为圈。 连通图:图G中,若任何两点之间,至少有一条链,则称G为连 通图,否则称为不连通图
定理1 图G=(V,E)中,所有点的次数之和等于边数的两倍。 这是显然的,因为在计算各点的次时,每条边都被用了两次。 次为奇数的点,称为奇点;次为偶数的点,称为偶点。 定理2 任一图中,奇点的个数必为偶数。 证明:设V1和V2分别是图中奇点和偶点的集合,q 为G中边的 个数,则 因为 是偶数,所以 也是偶数,从而中奇点个数必为 偶数个。 (v ) (v ) (vi ) q v i v i v i i i d d d 2 v v1 v 2 = + = ( ) i v v i v 2 d ( ) i v v i v1 d 链:图G中,点边交错序列{vi1ei1vi2ei2…vik },如果满足ei1=[vi1,vi2], ei2=[vi2,vi3],…,则称这个点边交错序列为vi1 到vik 的链。 圈:vi1= vik 的链称为圈。 连通图:图G中,若任何两点之间,至少有一条链,则称G为连 通图,否则称为不连通图

子图:设有图G=(V,E1),G2=(V2,E2),如果 V1sV2,EsE2,则称G1是G,的子图。 如果V1cV2,EcE2,则称G 是G,的真子图;如果V,=V2,E∈E,则称G1是G2的部分图。例如 图7-5中,(b)是(a)的真子图, (c)是(a)的部分图。 V1 V V, 0 (a) (b) (c) 图7-5
子图:设有图G1 =(V1,E1),G2 =(V2,E2),如果 则称G1是G2的子图。如果 则称G1 是G2的真子图;如果 则称G1是G2的部分图。例如 图7-5中,(b)是(a)的真子图,(c)是(a)的部分图。 V V ,E E , 1 2 1 2 V V ,E E , 1 2 1 2 V V ,E E , 1= 2 1 2 · · · · · v1 v2 v3 v4 v5 · · · · · · · · v1 ·v1 v2 v2 v3 v4 v v4 5 v5 (a) (b) (c) 图7-5
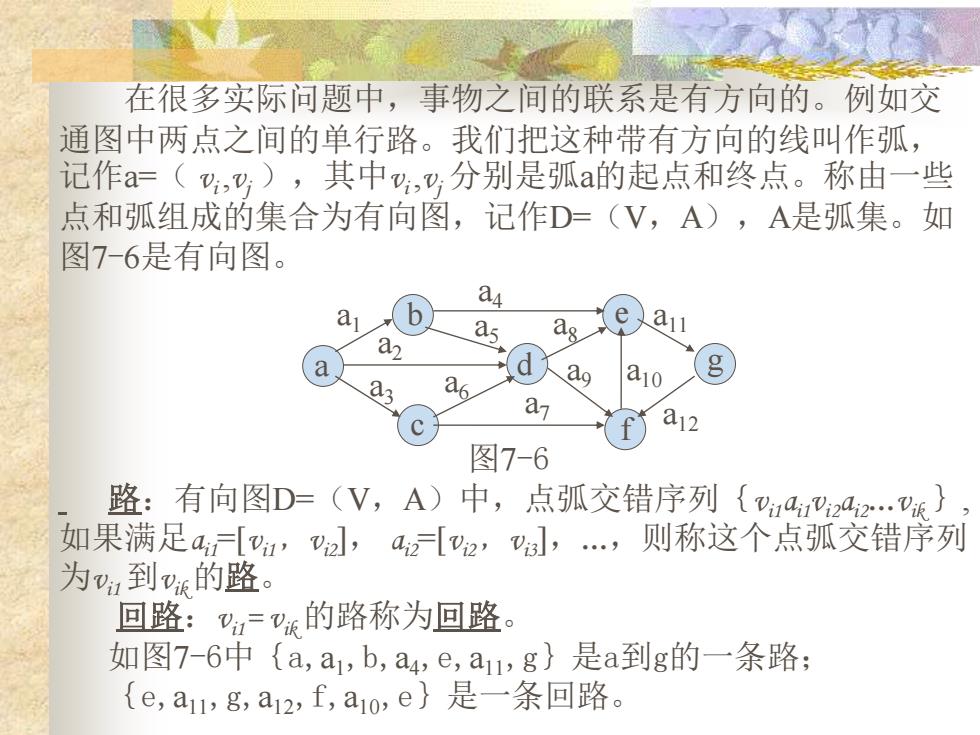
在很多实际问题中,事物之间的联系是有方向的。例如交 通图中两点之间的单行路。我们把这种带有方向的线叫作弧, 记作a=(,y),其中,y,分别是弧a的起点和终点。称由一些 点和弧组成的集合为有向图,记作D=(V,A),A是弧集。如 图7-6是有向图。 a a a a a a d a6 89 a10 a a12 图7-6 路:有向图D=(V,A)中,点弧交错序列{4a2.) 如果满足a,[u,v2,a2[2,, 则称这个点弧交错序列 为,到的路。 回路:=v的路称为回路。 如图7-6中{a,a,b,a4,e,a1,g}是a到g的一条路; {e,a11,g,a12,f,a1o,e}是一条回路
在很多实际问题中,事物之间的联系是有方向的。例如交 通图中两点之间的单行路。我们把这种带有方向的线叫作弧, 记作a=( vi ,vj ),其中vi ,vj 分别是弧a的起点和终点。称由一些 点和弧组成的集合为有向图,记作D=(V,A),A是弧集。如 图7-6是有向图。 a b c d e f g 图7-6 a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 路:有向图D=(V,A)中,点弧交错序列{vi1ai1vi2ai2…vik }, 如果满足ai1=[vi1,vi2], ai2=[vi2,vi3],…,则称这个点弧交错序列 为vi1 到vik 的路。 回路:vi1= vik 的路称为回路。 如图7-6中{a,a1,b,a4,e,a11,g}是a到g的一条路; {e,a11,g,a12,f,a10,e}是一条回路