
§3割平面法 割平面法是1958年美国学者R.E.Gomory提出的求解纯整数规 划的一种比较简便的方法,其基本思想是:先不考虑变量的整数限 制求解线性规划,如果得到的解不是整数解,则不断增加适当的约 束,割掉原可行域不含整数解的一部分,最终得到一个具有若干整 数顶点的可行域,而这些顶点中恰有一个项点是原问题的整数解。 割平面法的基本步骤: 步骤1不考虑变量的整数限制,求解相应的线性规划问题,如 果该问题无解,或最优解已是整数解,则停止计算,否则转下一步。 步骤2对上述线性规划的可行域进行“切割”,去掉不含整数 解的一部分可行域,即增加适当的线性约束,然后转步骤1
§3 割平面法 割平面法是1958年美国学者R.E.Gomory提出的求解纯整数规 划的一种比较简便的方法,其基本思想是:先不考虑变量的整数限 制求解线性规划,如果得到的解不是整数解,则不断增加适当的约 束,割掉原可行域不含整数解的一部分,最终得到一个具有若干整 数顶点的可行域,而这些顶点中恰有一个顶点是原问题的整数解。 割平面法的基本步骤: 步骤1 不考虑变量的整数限制,求解相应的线性规划问题,如 果该问题无解,或最优解已是整数解,则停止计算,否则转下一步。 步骤2 对上述线性规划的可行域进行“切割”,去掉不含整数 解的一部分可行域,即增加适当的线性约束,然后转步骤1

割平面法的关键在于如何确定切割方程,使之能对可行域进行 真正的切割,而且切去部分不含有整数解点。 下面讨论切割方程的求法。 设与整数规划相对应的线性规划最优解中基变量X=(Bb)不 是整数,将最优单纯形表中该基变量对应的行还原成约束方程,即 Xgi+2aX=(B-lb)月 (1) 将(Bb),a,都分解成整数与非负真分数之和的形式,即 (B-Ib);=N;+f 其中0<f<1 (2) ai-Ni+fi 其中0sf<1 (3) 这里N、N是整数,将2)、(3)代入(I),得 XBi+Σ(N+f)X=N+f 即 XBi +ENiXj-Ni=f-EfiXi (4) 当诸X:都是整数时,(④)式左端是整数,所以右端亦应是整数,但右 端是两个正数之差,且.0<£<1,∴.f-fX是小于1的整数,从
割平面法的关键在于如何确定切割方程,使之能对可行域进行 真正的切割,而且切去部分不含有整数解点。 下面讨论切割方程的求法。 设与整数规划相对应的线性规划最优解中基变量XBi=(B-1b)i不 是整数,将最优单纯形表中该基变量对应的行还原成约束方程,即 XBi +ΣaijXj=(B-1b)i ⑴ 将(B-1b)i,aij都分解成整数与非负真分数之和的形式,即 (B-1b)i=Ni+fi 其中0< fi <1 ⑵ aij=Nij+fij 其中0≤ fij <1 ⑶ 这里Ni、Nij是整数,将⑵、 ⑶代入⑴,得 XBi +Σ(Nij+fij)Xj=Ni+fi 即 XBi +ΣNijXj-Ni=fi-ΣfijXj ⑷ 当诸Xi都是整数时, ⑷式左端是整数,所以右端亦应是整数,但右 端是两个正数之差,且∵0< fi <1,∴ fi-ΣfijXj是小于1的整数,从

从而 ffXj0 (5) 取(⑤)式作为切割方程。因为任何整数可行解都满足这个方程,所以 把它加到原问题的约束中,它能够对原可行域进行切割,而不会切 割掉整数解。 例3用割平面法求解 maxZ=x +X2 -X1+x2≤1 3x1+x2≤4 X1,X2≥0, 整数 解:将问题标准化得 maxZ=X +X (1) -X1+x2+x3 =1 (2) 3x1+X2+x4=4 (3) X1X2≥0 (4) X1,X整数 (5) 不考虑条件(⑤),求解相应线性规划,结果见下表:
从而 fi-ΣfijXj≤0 ⑸ 取⑸式作为切割方程。因为任何整数可行解都满足这个方程,所以 把它加到原问题的约束中,它能够对原可行域进行切割,而不会切 割掉整数解。 例3 用割平面法求解 maxZ=x1+x2 -x1+x2 ≤1 3x1+x2 ≤4 x1 ,x2 ≥0,整数 解:将问题标准化得 maxZ=x1+x2 ⑴ -x1+x2+x3 =1 ⑵ 3x1+x2+x4 =4 ⑶ x1 ,x2 ≥0 ⑷ x1 ,x2 整数 ⑸ 不考虑条件⑸,求解相应线性规划,结果见下表:
C 1 0 0 CB B-ib X2 X3 X4 0 X3 1 -1 1 1 0 0 X4 4 3 1 0 1 O 0 1 1 0 0 ●eg ●●春 X1 3/4 1 0 -1/4 1/4 X2 714 0 1 3/4 1/4 O 0 0 -1/2 -1/2 表中X=3/4,不是整数,将表中第一行还原成方程,即 x1-1/4x+1/4x4=3/4 因为3/4=0+3/4,-1/4=-1+3/4,1/4=0+1/4 所以有 X1-x3-3/4-3/4x3-1/4x 因而有切割方程:3/4x+1/4x4≥3/4 即 3x3+x4≥3 引入松弛变量x,得方程-3x3x+x=-3 将新约束方程加到原最优表下面(切割),求得新的最优解如下:
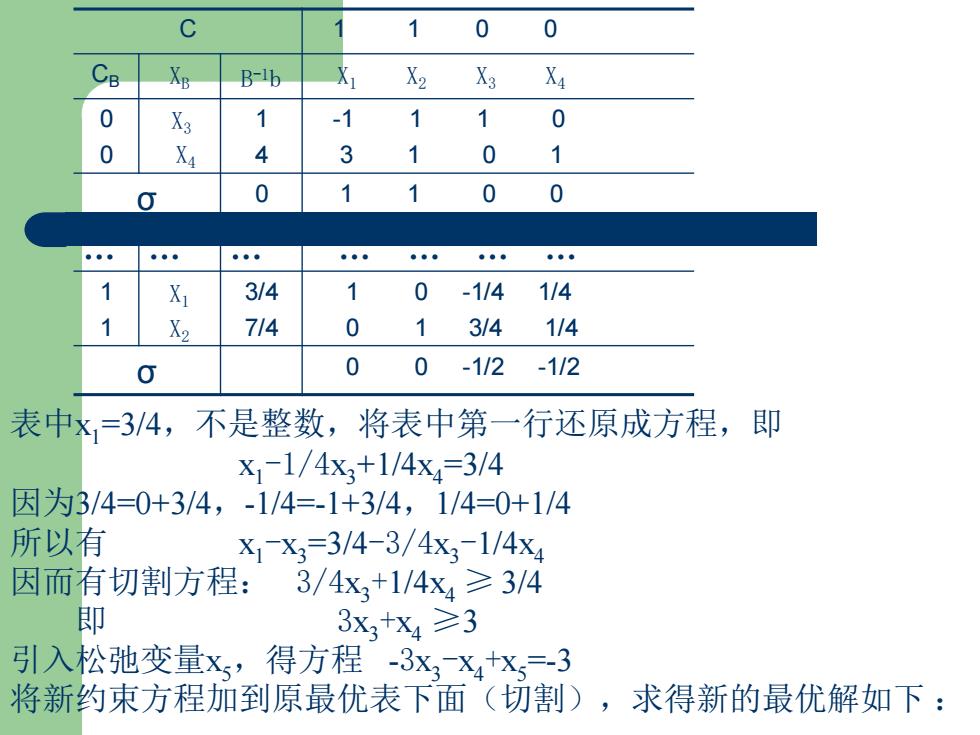
C 1 1 0 0 CB XB B -1b X1 X2 X3 X4 0 0 X3 X4 1 4 -1 1 1 0 3 1 0 1 σ 0 1 1 0 0 … … … … … … … 1 1 X1 X2 3/4 7/4 1 0 -1/4 1/4 0 1 3/4 1/4 σ 0 0 -1/2 -1/2 表中x1=3/4,不是整数,将表中第一行还原成方程,即 x1 -1/4x3+1/4x4=3/4 因为3/4=0+3/4,-1/4=-1+3/4,1/4=0+1/4 所以有 x1 -x3=3/4-3/4x3 -1/4x4 因而有切割方程: 3/4x3 +1/4x4 ≥ 3/4 即 3x3 +x4 ≥3 引入松弛变量x5,得方程 -3x3 -x4 +x5 =-3 将新约束方程加到原最优表下面(切割),求得新的最优解如下 :

C 1 1 0 0 0 4 B-ib 名 X2 X3 X4 X Xi 3/4 1 0 -1/4 1/4 0 X2 714 0 1 3/4 1/4 0 0 X 3 0 -3 -1 1 0 -1/2 -1/2 0 0 0 1/3 -1/12 X2 0 1 0 0 1/4 0 X 0 0 1/3-1/3 0 0 0 -1/3-1/6 由于x,x的值已是整数,所以该题经一次切割已得最优解: X=1,X2=1,最优值:Z※=2
C 1 1 0 0 0 CB XB B -1b X1 X2 X3 X4 X5 1 1 0 X1 X2 X5 3/4 7/4 -3 1 0 -1/4 1/4 0 0 1 3/4 1/4 0 0 0 -3 -1 1 σ 0 0 -1/2 -1/2 0 1 1 0 X1 X2 X3 1 1 1 1 0 0 1/3 -1/12 0 1 0 0 1/4 0 0 1 1/3 -1/3 σ 0 0 0 -1/3 -1/6 由于x1,x2的值已是整数,所以该题经一次切割已得最优解: x1=1,x2=1,最优值:Z※=2

现在我们来看看切割方程 3x3+x4≥3的几何意义。 例3对应的线性规划为 maxZ-x +X x1+x2≤1 3x1+x2≤4 X1,X2≥0 用图解法求得可行域D及最优解点A,见下图: X2 A(3/4,7/4) 由标准化的约束方程组可得 X3=1+x1X2 B(1, X=4-3x1X2 代入切割方程得 3x+x2=4 3(1+x1x2)+(4-3x1x2)≥3 即x,≤1,将此切割方程加入原约 束中,就等于切掉原可行域得 A1B部分,.如图 显然在AIB区域不含整数解点,对原可行域切割的结果是产生了一 个新顶点B,用图解法在新的可行域(黄色)中可求得整数最优解 恰是B(1,1)
现在我们来看看切割方程 3x3 +x4 ≥3 的几何意义。 例3对应的线性规划为 maxZ=x1+x2 -x1+x2 ≤1 3x1+x2 ≤4 x1 ,x2 ≥0 用图解法求得可行域D及最优解点A,见下图: x2 x1 1 -1 0 1 -x1+x2=1 3x1+x2=4 A(3/4,7/4) 由标准化的约束方程组可得 x3 =1+x1 -x2 x4=4 -3x1 -x2 代入切割方程 得 3(1+x1 -x2)+(4-3x1 -x2)≥3 即 x2 ≤1,将此切割方程 加入原约 束中,就等于切掉原可行域得 A1B部分,如图。 D B(1,1) 显然在A1B区域不含整数解点,对原可行域切割的结果是产生了一 个新顶点B,用图解法在新的可行域(黄色)中可求得整数最优解 恰是B(1,1)

在求解实际问题中,割平面法经常会遇到收敛很慢的情 况,但若和其它方法,如分枝定界法,联合使用,一般能收 到比较好的效果
在求解实际问题中,割平面法经常会遇到收敛很慢的情 况,但若和其它方法,如分枝定界法,联合使用,一般能收 到比较好的效果