
丰 ,國级 第一章线性规划与单纯形法 粥 §5单纯形法的进一步讨论 5.1两阶段法 对于前面介绍的大M法,如果用计算机求解时,只能用很大的 正数代替M,这就可能造成计算上的错误。下面介绍不须要引进相 当大正数M的两阶段法。 第一阶段,求初始基可行解:在约束中添加人工变量,使约束 矩阵出现单位子矩阵,然后以这些人工变量之和的相反数W求最大 为目标函数,进行求解。若第一阶段最优解对应的最优值等于零, 则所有人工变量一定都取零值,说明原问题存在基可行解,可以进 行第二阶段计算,否则原问题无可行解,应停止计算。 第二阶段,求原问题的最优解:将第一阶段计算得到的最终表 除去人工变量,恢复原来的目标函数,并以第一阶段的最优解为初 始基可行解,重新计算检验数,然后用单纯形法继续求解
第一章 线性规划与单纯形法 §5 单纯形法的进一步讨论 5.1 两阶段法 对于前面介绍的大M法,如果用计算机求解时,只能用很大的 正数代替M,这就可能造成计算上的错误。下面介绍不须要引进相 当大正数M的两阶段法。 第一阶段,求初始基可行解:在约束中添加人工变量,使约束 矩阵出现单位子矩阵,然后以这些人工变量之和的相反数W求最大 为目标函数,进行求解。若第一阶段最优解对应的最优值等于零, 则所有人工变量一定都取零值,说明原问题存在基可行解,可以进 行第二阶段计算,否则原问题无可行解,应停止计算。 第二阶段,求原问题的最优解:将第一阶段计算得到的最终表, 除去人工变量,恢复原来的目标函数,并以第一阶段的最优解为初 始基可行解,重新计算检验数,然后用单纯形法继续求解

國@欧双 例9 用两阶段法求解下列线性规划 maxZ-3x1-X2-X3 X1-2x2+X3≤11 -4x1+x2+2X3≥3 2x1+31 X1,X2,X3≥0 解加入松弛变量及人工变量,给出第一阶段数学模型: maxW=-X6-X7 X1-2x2+X3+X4 =11 -4x1+x2+2X3 X5+X6=3 -2x1 +X3 +x7=1 X1,X2,X3, X4)X5,X6,X7≥0 取(P,P6,P,)为初始基B,列出初始单纯形表, 并计算如下:
例9 用两阶段法求解下列线性规划 maxZ=3x1 -x2 -x3 x1 -2x2 + x3≤11 -4x1 + x2 +2X3≥3 -2x1 + x3 =1 x1 ,x2 ,x3 ≥0 解 加入松弛变量及人工变量,给出第一阶段数学模型: maxW=-x6-x7 x1 -2x2 + x3 +x4 =11 -4x1 + x2 +2X3 -x5+x6 =3 -2x1 + x3 +x7=1 x1 ,x2 ,x3 , x4 , x5 , x6,x7≥0 取(P4 , P6,P7)为初始基B,列出初始单纯形表,并计算如下:
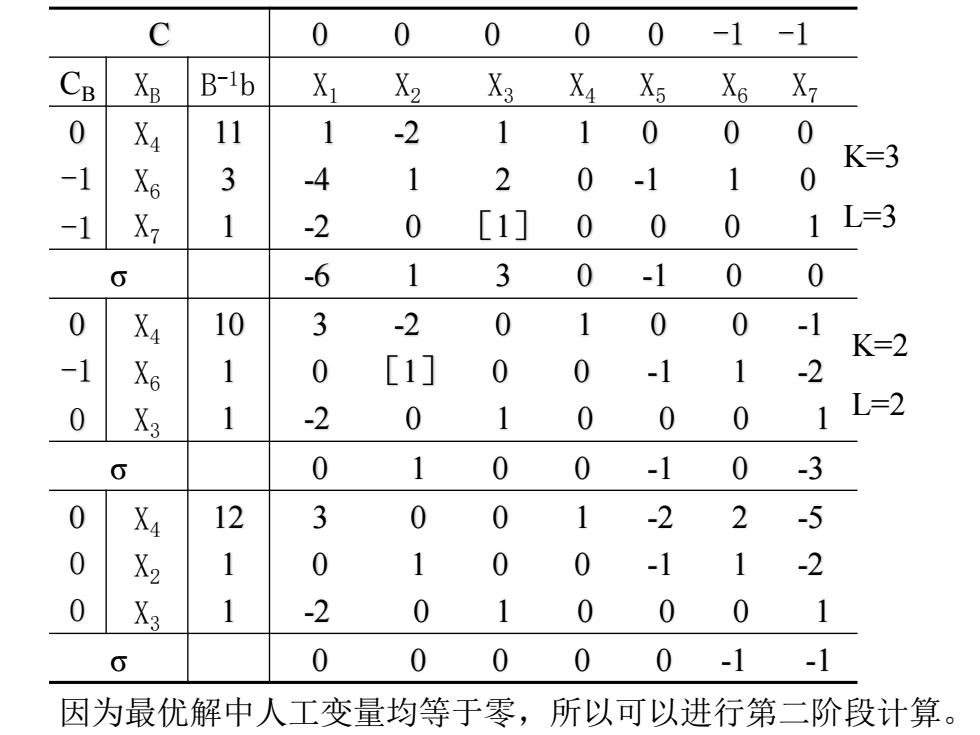
C 0 0 0 0 0 -1 -1 CB Xp B-ib X X2 X3 X4 Xs X6 X7 0 X4 11 1 -2 1 1 0 0 0 K=3 -1 X6 3 -4 1 2 0 -1 1 0 -1 X7 1 -2 0 [1] 0 0 0 1L=3 0 -6 1 3 0 -1 0 0 0 Xa 10 3 -2 0 1 0 0 -1 K=2 -1 Xs 1 0 [1] 0 0 -1 1 -2 0 X3 1 -2 0 1 0 0 0 1L=2 0 1 0 0 -1 0 -3 0 X4 12 3 0 0 1 -2 2 -5 0 X2 1 0 1 0 0 -1 1 -2 0 X 1 -2 0 1 0 0 0 1 0 0 0 0 0 0 -1 -1 因为最优解中人工变量均等于零,所以可以进行第二阶段计算
C 0 0 0 0 0 -1 -1 CB XB B -1b X1 X2 X3 X4 X5 X6 X7 0 -1 -1 X4 X6 X7 11 3 1 1 -2 1 1 0 0 0 -4 1 2 0 -1 1 0 -2 0 [1] 0 0 0 1 σ -6 1 3 0 -1 0 0 0 -1 0 X4 X6 X3 10 1 1 3 -2 0 1 0 0 -1 0 [1] 0 0 -1 1 -2 -2 0 1 0 0 0 1 σ 0 1 0 0 -1 0 -3 0 0 0 X4 X2 X3 12 1 1 3 0 0 1 -2 2 -5 0 1 0 0 -1 1 -2 -2 0 1 0 0 0 1 σ 0 0 0 0 0 -1 -1 K=3 L=3 K=2 L=2 因为最优解中人工变量均等于零,所以可以进行第二阶段计算
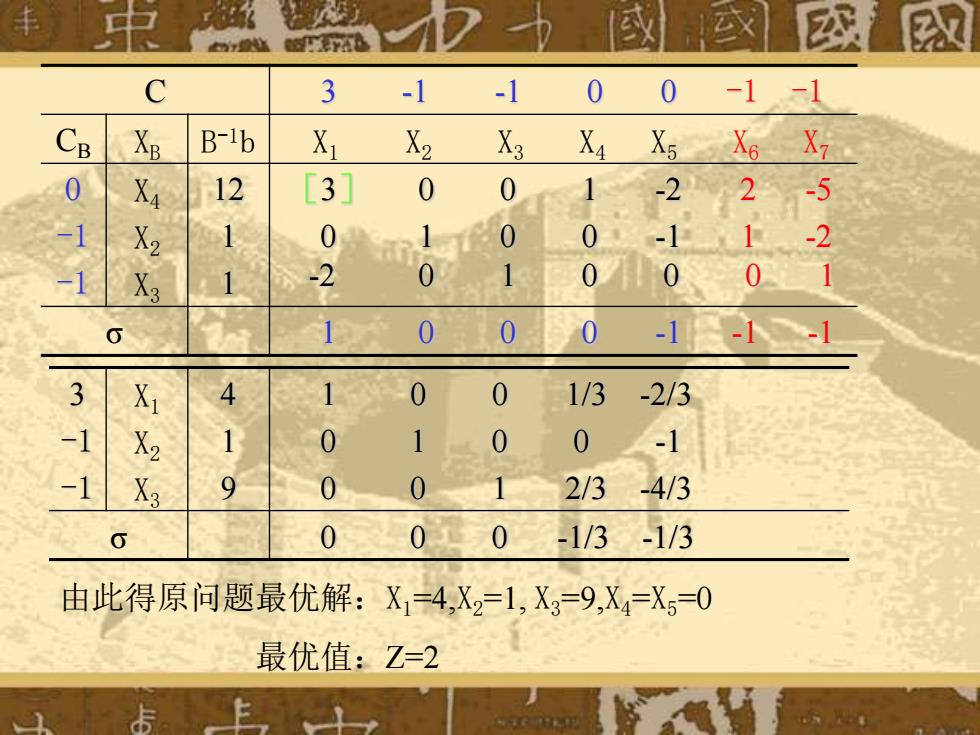
3 -1 0 -1 -1 CB B-ib X1 X2 X3 X4 X5 X6 X7 Xa 12 [3] 0 01 -22-5 X2 0 10 0 -1 1-2 X3 -2 0 0 0 0 1 0 0 0 -1-1 4 1 0 0 1/3 -2/3 X2 1 0 1 0 0 -1 0 0 2/3-4/3 0 00 -1/3-1/3 由此得原问题最优解:X1=4,X2=1,X3=9,X4=X=0 最优值:Z=2
C 3 -1 -1 0 0 -1 -1 CB XB B -1b X1 X2 X3 X4 X5 X6 X7 0 -1 -1 X4 X2 X3 12 1 1 [3] 0 0 1 -2 2 -5 0 1 0 0 -1 1 -2 -2 0 1 0 0 0 1 σ 1 0 0 0 -1 -1 -1 3 -1 -1 X1 X2 X3 4 1 9 1 0 0 1/3 -2/3 0 1 0 0 -1 0 0 1 2/3 -4/3 σ 0 0 0 -1/3 -1/3 由此得原问题最优解:X1=4,X2=1, X3=9,X4=X5=0 最优值:Z=2

5.2退化与循环 单纯形算法中,基变量一般都取非零值,非基变量都取零值, 如果某个基可行解中存在取零值的基变量,则称该解为退化解。在 退化情况下,如果取退化的基变量为旋出变量,则变换后的解仍为 退化解,且目标函数值不变,在以后的迭代中,如果每次都取退化 的基变量为旋出变量,则迭代可能只在可行域的几个顶点中反复进 行,即出现计算过程的循环,而达不到最优解。 为了避免出现循环问题,1974年Bland:提出一种简便的规则: ①若k=min {jo;>0},则以xk(脚标最小的非基变量)为 旋入变量。 ②计算0=min{(B-b)i/ak|ak>0},当存在两个或两个以上比 值都等于0时,选取脚标最小的基变量为换出变量。 可以证明,按Bland规则计算时,一定可以避免循环。 实际计算中,循环现象极为罕见,目前仅有人为构造的几个例 子会出现循环现象,因此,我们计算时完全可以不必考虑循环问题
5.2 退化与循环 单纯形算法中,基变量一般都取非零值,非基变量都取零值, 如果某个基可行解中存在取零值的基变量,则称该解为退化解。在 退化情况下,如果取退化的基变量为旋出变量,则变换后的解仍为 退化解,且目标函数值不变,在以后的迭代中,如果每次都取退化 的基变量为旋出变量,则迭代可能只在可行域的几个顶点中反复进 行,即出现计算过程的循环,而达不到最优解。 为了避免出现循环问题,1974年Bland提出一种简便的规则: ①若 k=min{j│σj >0},则以xk(脚标最小的非基变量)为 旋入变量。 ②计算θ=min{(B -1b)i/aik│aik>0},当存在两个或两个以上比 值都等于θ时,选取脚标最小的基变量为换出变量。 可以证明,按Bland规则计算时,一定可以避免循环。 实际计算中,循环现象极为罕见,目前仅有人为构造的几个例 子会出现循环现象,因此,我们计算时完全可以不必考虑循环问题

5.3标准型的其它形式 有的教材定义线性规划的标准型为: minZ=CX AX=b X≥0 如果仍定义检验数为o,=CCB-P; 由目标函数的表达式 Z=CB-b+∑,0X j=m+1 易知,以目标函数极小化为标准型的线性规划问题的最优性检验 规则为:对某基可行解X=B-b,其余x;0,若所有检验数 0;=Cj-CB-P,≥0,j=m+1m+2,n 则该解为最优解
5.3 标准型的其它形式 有的教材定义线性规划的标准型为: minZ= CX AX=b X≥0 如果仍定义检验数为 由目标函数的表达式 易知,以目标函数极小化为标准型的线性规划问题的最优性检验 规则为:对某基可行解 XB =B -1b,其余xj=0,若所有检验数 则该解为最优解。 ,j 1 j j B σ C -C B P = − = + = + − n j m 1 j j 1 B Z C B b σx = + + = − 0,j m 1,m 2,,n j 1 j j B σ C -C B P